Три еквивалентни определения на непрекъсната в точка функция. непрекъсната функция

Теорема. Нека функцията x=φ(t)непрекъснато в точка а, и функцията y=f(x)непрекъснато в точка b=φ(a). След това сложната функция y=f[φ(t)]=F(t)непрекъснато в точка а.

Позволявам x=φ(t)и y=f(x)са най-простите елементарни функции и множеството от стойности (х)функции x=φ(t)е обхватът на функцията y=f(x). Както знаем, елементарните функции са непрекъснати във всяка точка от областта на задачите. Следователно, съгласно предишната теорема, комплексната функция y=f(φ(t)), тоест суперпозицията на две елементарни функции, е непрекъсната. Например функцията е непрекъсната във всяка точка x ≠ 0, като сложна функция от две елементарни функции х=t-1и y=sin x. Също така функция y=ln sin xнепрекъснато във всяка точка от интервалите (2kπ,(2k+1)π), k ∈ Z (sinx>0).

1. Въведение.

2. Определение за непрекъснатост на функция.

3. Класификация на точките на прекъсване

4. Свойства на непрекъснатите функции.

5. Икономически смисъл на приемствеността.

6. Заключение.

10.1. Въведение

Всеки път, оценявайки неизбежните промени в заобикалящия ни свят във времето, ние се опитваме да анализираме протичащите процеси, за да подчертаем техните най-съществени характеристики. Един от първите въпроси по този път е: какнастъпват промени, които са характерни за това явление - непрекъснатоили дискретно, т.е. спазматично. Дали валутата се обезценява равномерно или се срива, има ли постепенна еволюция или революционен скок? За да се унифицират качествените и количествените оценки на случващото се, трябва да се абстрахираме от конкретното съдържание и да изследваме проблема от гледна точка на функционална зависимост. Това ни позволява да направим теорията на границите, която разгледахме в последната лекция.

10.2. Определяне на непрекъснатостта на функция

Непрекъснатостта на функцията е интуитивно свързана с факта, че нейната графика е непрекъсната, никъде не прекъсвана крива. Начертаваме графика на такава функция, без да вдигаме писалката от хартията. Ако една функция е дадена в таблица, тогава нейната непрекъснатост, строго погледнато, не може да се прецени, тъй като за дадена стъпка от таблицата поведението на функцията в интервалите не е определено.

В действителност при непрекъснатост се осъществява следното обстоятелство: ако параметрите, характеризиращи ситуацията малкопромени тогава малкоситуацията също ще се промени. Важното тук е не че ситуацията ще се промени, а че ще се промени „малко“.

Нека формулираме концепцията за непрекъснатост на езика на нарастванията. Нека дадено явление се описва с функция и точка апринадлежи към обхвата на функцията. Разликата се нарича увеличение на аргументав точката а, разликата е увеличение на функциятав точката а.

Определение 10.1.функция непрекъснато в точка a, ако е дефиниран в тази точка и безкрайно малко увеличение на аргумента съответства на безкрайно малко увеличение на функцията:

Пример 10.1.Изследване за непрекъснатост на функция в точка.

Решение.Нека изградим графика на функцията и да отбележим нарастванията D върху нея хи Д г(фиг. 10.1).

От графиката може да се види, че колкото по-малко е увеличението D х, толкова по-малко D г. Нека покажем това аналитично. Увеличението на аргумента е , тогава нарастването на функцията в тази точка ще бъде равно на

Това показва, че ако , тогава и :

.

Нека дадем още едно определение за непрекъснатост на функция.

Определение 10.2.Функцията се извиква непрекъснатов точка а, ако:

1) тя е определена в точката a и някои от нейните околности;

2) едностранни граници съществуват и са равни една на друга:

;

3) граница на функцията при x® a е равно на стойността на функцията в тази точка:

.

Ако поне едно от тези условия е нарушено, тогава се казва, че функцията претърпява празнина.

Това определение работи за установяване на приемственост в даден момент. Следвайки неговия алгоритъм и отбелязвайки съвпаденията и несъответствията между изискванията на дефиницията и конкретен пример, можем да заключим, че функцията е непрекъсната в точка.

Определение 2 ясно показва идеята за близост, когато въведохме концепцията за граница. С неограничено приближение на аргумента хза ограничаване на стойността а, непрекъснато в точката афункция f(х) произволно близо до граничната стойност f(а).

10.3. Класификация на точките на прекъсване

Точките, в които се нарушават условията за непрекъснатост на дадена функция, се наричат преломни точкитази функция. Ако х 0 е точката на прекъсване на функцията, в нея не е изпълнено поне едно от условията за непрекъснатост на функцията. Помислете за следния пример.

1. Функцията е дефинирана в някаква околност на точката а, но не е дефиниран в самата точка а. Например функцията не е дефинирана в точката а=2, така че претърпява прекъсване (виж Фиг. 10.2).

Ориз. 10.2 Фиг. 10.3

2. Функцията е дефинирана в точка аи в някаква близост от него съществуват неговите едностранни граници, но не са равни една на друга: , тогава функцията претърпява прекъсване. Например функцията

се дефинира в точката обаче, когато функцията изпитва прекъсване (виж Фиг. 10.3), тъй като

и ().

3. Функцията е дефинирана в точка аи в някои от неговите околности има граница на функцията при , но тази граница не е равна на стойността на функцията в точката а:

.

Например функция (вижте Фигура 10.4)

Ето я преломната точка:

,

Всички точки на прекъсване са разделени на отстраняеми точки на прекъсване, точки на прекъсване от първи и втори вид.

Определение 10.1.Точката на прекъсване се нарича точка ремонтируема празнина , ако в тази точка има крайни граници на функцията отляво и отдясно, равни една на друга:

.

Границата на функцията в тази точка съществува, но не е равна на стойността на функцията в граничната точка (ако функцията е дефинирана в граничната точка), или функцията в граничната точка не е дефинирана.

На фиг. 10.4 в точката, условията за непрекъснатост са нарушени и функцията има прекъсване. Точка (0; 1) на графиката издълбан. Тази празнина обаче може лесно да бъде премахната - достатъчно е да предефинирате дадената функция, като я зададете равна на нейната граница в тази точка, т.е. слагам . Следователно такива пропуски се наричат ​​​​подвижни.

Определение 10.2.Точката на прекъсване се нарича точка на прекъсване от 1-ви род , ако в тази точка има крайни граници на функцията отляво и отдясно, но те не са равни една на друга:

.

В този момент се казва, че функцията преживява скок.

На фиг. 10.3 функцията има прекъсване от 1-ви род в точката . Границите отляво и отдясно в тази точка са равни:

и .

Скокът на функцията в точката на прекъсване е равен на .

Невъзможно е такава функция да се разшири до непрекъсната. Графиката се състои от две полулинии, разделени със скок.

Определение 10.3.Точката на прекъсване се нарича точка на счупване от 2-ри вид ако поне една от едностранните граници на функцията (лява или дясна) не съществува или е равна на безкрайност.

На фигура 10.3 функцията в точка има прекъсване от 2-ри род. Разглежданата функция при е безкрайно голяма и няма краен предел нито отдясно, нито отляво. Следователно не е необходимо да се говори за приемственост в такъв момент.

Пример 10.2.Изградете графика и определете естеството на точките на прекъсване:

Решение.Нека начертаем функцията f(х) (Фигура 10.5).

От фигурата може да се види, че оригиналната функция има три точки на прекъсване: , х 2 = 1,
х 3 = 3. Разгледайте ги по ред.

Следователно точката има разкъсване от 2-ри вид.

а) Функцията е дефинирана в тази точка: f(1) = –1.

б) , ,

тези. в точката х 2 = 1 наличен ремонтируема празнина. Чрез замяна на стойността на функцията в този момент: f(1) = 5, прекъсването се елиминира и функцията става непрекъсната в тази точка.

а) Функцията е дефинирана в тази точка: f(3) = 1.

Така че по същество х 1 = 3 налични разкъсване от 1-ви вид. Функцията в тази точка изпитва скок, равен на D г= –2–1 = –3.

10.4. Свойства на непрекъснатите функции

Като си припомним съответните свойства на границите, заключаваме, че функция, която е резултат от аритметични операции върху функции, непрекъснати в една и съща точка, също е непрекъсната. Забележка:

1) ако функциите и са непрекъснати в точка а, тогава функциите , и (при условие, че ) също са непрекъснати в тази точка;

2) ако функцията е непрекъсната в точка аи функцията е непрекъсната в точката , тогава съставната функция е непрекъсната в точката аи

,

тези. знакът на границата може да се постави под знака на непрекъснатата функция.

Казват, че една функция е непрекъсната в някакво множество, ако е непрекъсната във всяка точка от това множество. Графиката на такава функция е непрекъсната линия, която се зачертава с едно натискане на писалката.

Всички основни елементарните функции са непрекъснати във всички точки, където са дефинирани.

Функции, непрекъснати на сегмента, имат редица важни отличителни свойства. Нека формулираме теореми, изразяващи някои от тези свойства.

Теорема 10.1 (Теорема на Вайерщрас ). Ако функцията е непрекъсната на сегмент, тогава тя достига своите минимални и максимални стойности на този сегмент.

Теорема 10.2 (Теорема на Коши ). Ако функцията е непрекъсната на сегмент, тогава всички междинни стойности между най-малката и най-голямата стойност са на този сегмент.

Следното важно свойство следва от теоремата на Коши.

Теорема 10.3. Ако функцията е непрекъсната на сегмент и приема стойности на различни знаци в краищата на сегмента, тогава между a и b има точка c, в която функцията изчезва:.

Геометричният смисъл на тази теорема е очевиден: ако графиката на непрекъсната функция преминава от долната полуравнина към горната (или обратно), тогава поне в една точка тя ще пресече оста вол(фиг.10.6).

Пример 10.3.Изчислете приблизително корена на уравнението

, (т.е. приблизително замени) полином от съответната степен.

Това свойство на непрекъснатите функции е много важно за практиката. Например, много често непрекъснатите функции се дават чрез таблици (наблюдателни или експериментални данни). След това, използвайки произволен метод, можете да замените табличната функция с полином. В съответствие с теорема 10.3 това винаги може да се направи с достатъчно висока точност. Работата с аналитично зададена функция (особено с полином) е много по-лесна.

10.5. Икономическият смисъл на приемствеността

Повечето от функциите, използвани в икономиката, са непрекъснати и това ни позволява да правим доста значими твърдения с икономическо съдържание.

Като илюстрация разгледайте следния пример.

данъчна ставка нима графика, подобна на фиг. 10.7а.

В краищата на празнините е прекъснат и тези прекъсвания са от първи род. Въпреки това, размерът на данъка върху доходите П(фиг. 10.7b) е непрекъсната функция на годишния доход Q. От това по-специално следва, че ако годишните доходи на двама души се различават незначително, то разликата в размера на данъка върху доходите, който те трябва да платят, също трябва да се различава незначително. Интересно е, че обстоятелството се възприема от по-голямата част от хората като напълно естествено, над което дори не се замислят.

10.6. Заключение

В крайна сметка нека направим малко отклонение.

Ето как да изразим графично тъжното наблюдение на древните:

Sic transit Gloria mundi …

(Така минава земната слава …)

Край на работата -

Тази тема принадлежи на:

Функционална концепция

Концепцията за функция.. всичко тече и всичко се променя Хераклит.. таблица x x x x y y y y y y y y

Ако имате нужда от допълнителен материал по тази тема или не сте намерили това, което търсите, препоръчваме да използвате търсенето в нашата база данни с произведения:

Какво ще правим с получения материал:

Ако този материал се оказа полезен за вас, можете да го запазите на страницата си в социалните мрежи:

Определение
функция f (х)Наречен непрекъснато при х 0 околност на тази точка и ако границата като x клони към x 0 е равно на стойността на функцията при x 0 :
.

Използвайки дефинициите на Коши и Хайне за границата на функция, може да се даде подробни дефиниции на непрекъснатостта на функция в точка .

Човек може да формулира понятието приемственост в условия на увеличения. За да направим това, въвеждаме нова променлива, която се нарича нарастване на променливата x в точката. Тогава функцията е непрекъсната в точката if
.
Нека представим нова функция:
.
Викат я увеличение на функциятав точка . Тогава функцията е непрекъсната в точката if
.

Дефиниране на непрекъснатост вдясно (вляво)
функция f (х)Наречен непрекъснато отдясно (вляво) в точката x 0 , ако е дефиниран в някаква дясна (лява) околност на тази точка и ако дясната (лявата) граница в точката x 0 е равно на стойността на функцията при x 0 :
.

Теорема за ограничеността на непрекъсната функция
Нека функцията f (х)непрекъснато при х 0 . Тогава съществува квартал U (x0)върху които функцията е ограничена.

Теорема за запазване на знака на непрекъсната функция
Нека функцията е непрекъсната в точката . И нека има положителна (отрицателна) стойност в този момент:
.
Тогава има такава околност на точката, в която функцията има положителна (отрицателна) стойност:
при .

Аритметични свойства на непрекъснати функции
Нека функциите и са непрекъснати в точката .
Тогава функциите и са непрекъснати в точката.
Ако , тогава функцията също е непрекъсната в точката .

Свойство за лява и дясна непрекъснатост
Една функция е непрекъсната в точка тогава и само ако е непрекъсната отдясно и отляво.

Доказателствата за свойствата са дадени на страницата "Свойства на функции, непрекъснати в точка".

Непрекъснатост на сложна функция

Теорема за непрекъснатост на комплексна функция
Нека функцията е непрекъсната в точката . И нека функцията е непрекъсната в точката .
Тогава комплексната функция е непрекъсната в точката .

Граница на сложна функция

Теорема за границата на непрекъсната функция на функция
Нека има граница на функцията при и тя е равна на:
.
Тук точка t 0 може да бъде краен или безкрайно: .
И нека функцията е непрекъсната в точката .
Тогава има граница на комплексната функция и тя е равна на:
.

Теорема за граница на комплексна функция
Нека функцията има граница и съпоставете пунктирания квартал на точката върху пунктирания квартал на точката. Нека функцията е дефинирана в тази околност и има ограничение върху нея.
Тук - крайни или безкрайно отдалечени точки: . Кварталите и съответните им граници могат да бъдат както двустранни, така и едностранни.
Тогава има граница на комплексната функция и тя е равна на:
.

точки на прекъсване

Определяне на точката на прекъсване
Нека функцията е дефинирана в някаква пунктирана околност на точката. Точката се нарича точка на прекъсване на функциятаако е изпълнено едно от двете условия:
1) не е дефинирано в ;
2) е дефиниран в , но не е в тази точка.

Определяне на точката на прекъсване от 1-ви вид
Точката се нарича точка на счупване от първи вид, ако е точка на прекъсване и има ограничени едностранни граници отляво и отдясно:
.

Определение за скок на функция
Функция Jump Δв точка се нарича разликата между границите отдясно и отляво
.

Определяне на точка на прекъсване
Точката се нарича точка на пречупванеако има ограничение
,
но функцията в точката или не е дефинирана, или не е равна на граничната стойност: .

По този начин точката на прекъсване е точка на прекъсване от 1-ви вид, в която скокът на функцията е равен на нула.

Определяне на точката на прекъсване от 2-ри вид
Точката се нарича точка на счупване от втори вид, ако не е точка на прекъсване от 1-ви род. Тоест, ако няма поне една едностранна граница или поне една едностранна граница в точка е равна на безкрайност.

Свойства на функции, непрекъснати на интервал

Определение на функция, непрекъсната на отсечка
Една функция се нарича непрекъсната на отсечка (за ), ако е непрекъсната във всички точки от отворения интервал (за ) и съответно в точки a и b .

Първата теорема на Вайерщрас за ограничеността на непрекъсната на интервал функция
Ако една функция е непрекъсната на сегмент, тогава тя е ограничена на този сегмент.

Определяне на достижимостта на максимума (минимума)
Функцията достига своя максимум (минимум) в множеството, ако има аргумент за който
за всички .

Определяне на достижимостта на горната (долната) граница
Една функция достига своята горна (долна) граница на множеството, ако има аргумент за който
.

Втората теорема на Вайерщрас за максимума и минимума на непрекъсната функция
Функция, непрекъсната върху сегмент, достига своите горни и долни граници върху него или, което е едно и също нещо, достига своя максимум и минимум върху сегмента.

Теорема за междинната стойност на Болцано-Коши
Нека функцията е непрекъсната на интервала . И нека C е произволно число между стойностите на функцията в краищата на сегмента: и . След това има точка, за която
.

Следствие 1
Нека функцията е непрекъсната на интервала . И нека стойностите на функцията в краищата на сегмента имат различни знаци: или. Тогава има точка, в която стойността на функцията е равна на нула:
.

Следствие 2
Нека функцията е непрекъсната на интервала . Остави . Тогава функцията приема на сегмента всички стойности от и само тези стойности:
при .

Обратни функции

Дефиниция на обратната функция
Нека функцията има домейн X и набор от стойности Y . И нека има свойството:
за всички .
Тогава за всеки елемент от множеството Y може да се асоциира само един елемент от множеството X, за което . Това съответствие дефинира функция, наречена обратна функцияда се . Обратната функция се означава по следния начин:
.

От дефиницията следва, че
;
за всички ;
за всички .

Лема за взаимната монотонност на права и обратна функция
Ако една функция е строго нарастваща (намаляваща), тогава има обратна функция, която също е строго нарастваща (намаляваща).

Свойство за симетрията на графики на преки и обратни функции
Графиките на правата и обратната функция са симетрични спрямо правата линия.

Теорема за съществуването и непрекъснатостта на обратната функция върху отсечка
Нека функцията е непрекъсната и строго нарастваща (намаляваща) на интервала. Тогава на интервала е определена и непрекъсната обратната функция, която е строго нарастваща (намаляваща).

За нарастваща функция. За спускане - .

Теорема за съществуването и непрекъснатостта на обратната функция на интервал
Нека функцията е непрекъсната и строго нарастваща (намаляваща) на отворен краен или безкраен интервал. Тогава обратната функция е определена и непрекъсната на интервала, който е строго нарастващ (намаляващ).

За нарастваща функция.
За слизане: .

По подобен начин може да се формулира теорема за съществуването и непрекъснатостта на обратна функция на полуинтервал.

Свойства и непрекъснатост на елементарните функции

Елементарните функции и техните обратни са непрекъснати в тяхната област на дефиниране. По-нататък даваме формулировки на съответните теореми и даваме препратки към техните доказателства.

Експоненциална функция

експоненциална функция f (x) = x, с основа а > 0 е границата на последователността
,
където е произволна последователност от рационални числа, клоняща към x:
.

Теорема. Свойства на експоненциалната функция
Експоненциалната функция има следните свойства:
(P.0)е дефинирано, за , за всички ;
(P.1)когато a ≠ 1 има много значения;
(P.2)стриктно нараства при , стриктно намалява при , е постоянен при ;
(P.3) ;
(P.3*) ;
(P.4) ;
(P.5) ;
(P.6) ;
(P.7) ;
(P.8)е непрекъснат за всички;
(P.9)в ;
при .

Логаритъм

Логаритмична функция, или логаритъм, y = log x, с основа ае обратната на експоненциалната функция с основа а.

Теорема. Свойства на логаритъма
Логаритмична функция с основа a, y = дневник x, има следните свойства:
(L.1)е дефиниран и непрекъснат, за и , за положителни стойности на аргумента,;
(L.2)има много значения;
(L.3)стриктно нараства при , стриктно намалява при ;
(L.4)в ;
в ;
(L.5) ;
(L.6)в ;
(L.7)в ;
(L.8)в ;
(L.9)при .

Експонента и натурален логаритъм

В дефинициите на експоненциалната функция и логаритъма фигурира константата a, която се нарича основа на степента или основа на логаритъма. В математическия анализ в по-голямата част от случаите се получават по-прости изчисления, ако числото e се използва като основа:
.
Експоненциална функция с основа e се нарича експонента: , а логаритъмът при основа e се нарича натурален логаритъм: .

Свойствата на експонентата и натуралния логаритъм са изложени на страници
"Експонента, e на степен x",
„Натурален логаритъм, функция ln x“

Силова функция

Степенна функция с показател pе функцията f (x) = xp, чиято стойност в точката x е равна на стойността на експоненциалната функция с основа x в точката p .
В допълнение, f (0) = 0 p = 0за p > 0 .

Тук разглеждаме свойствата на степенната функция y = x p за неотрицателни стойности на аргумента. За рационално, за нечетно m, експоненциалната функция е дефинирана за отрицателно x. В този случай неговите свойства могат да бъдат получени с помощта на четно или нечетно.
Тези случаи са обсъдени и илюстрирани подробно на страницата Power Function, Its Properties and Graphs.

Теорема. Свойства на степенната функция (x ≥ 0)
Степенна функция, y = x p, с показател p има следните свойства:
(C.1)определени и непрекъснати на множеството
в ,
при ".

Тригонометрични функции

Теорема за непрекъснатост на тригонометрични функции
Тригонометрични функции: синус ( грях х), косинус ( cos x), допирателна ( tg x) и котангенс ( ctg x

Теорема за непрекъснатост на обратни тригонометрични функции
Обратни тригонометрични функции: арксинус ( arcsin x), аркосинус ( arccos x), аркутангенс ( arctg x) и аркутангенса ( arcctg x) са непрекъснати в техните области на дефиниция.

Препратки:
О.И. Демони. Лекции по математически анализ. Част 1. Москва, 2004 г.
Л.Д. Кудрявцев. Курс по математически анализ. Том 1. Москва, 2003 г.
СМ. Николски. Курс по математически анализ. Том 1. Москва, 1983 г.

Помислете за две функции, чиито графики са показани на фиг. 1 и 2. Графиката на първата функция може да се начертае, без да се вдига моливът от хартията. Тази функция може да се нарече непрекъсната. Невъзможно е да се начертае графика на друга функция по този начин. Състои се от две непрекъснати части и в една точка има прекъсване и ще наричаме функцията прекъсната.

Такава визуална дефиниция на непрекъснатостта не може да подхожда по никакъв начин на математиката, тъй като съдържа напълно нематематически понятия за "молив" и "хартия". Точната математическа дефиниция на непрекъснатостта е дадена на базата на понятието граница и се състои в следното.

Нека функцията е дефинирана на отсечка и е някаква точка от тази отсечка. Функцията се нарича непрекъсната в точка, ако, както се стреми към (разглежда се само от сегмент), стойностите на функцията се стремят към, т.е. ако

. (1)

Една функция се нарича непрекъсната на сегмент, ако е непрекъсната във всяка точка от него.

Ако равенството (1) не е изпълнено в точката, функцията се нарича прекъсната в точката .

Както можем да видим, математически свойството за непрекъснатост на функция върху сегмент се определя чрез локалното (локално) свойство за непрекъснатост в точка.

Стойността се нарича увеличение на аргумента, разликата между стойностите на функцията се нарича увеличение на функцията и се обозначава с . Очевидно, когато се стреми към нарастване на аргумента клони към нула: .

Нека пренапишем равенството (1) в еквивалентна форма

.

Използвайки въведената нотация, тя може да бъде пренаписана, както следва:

Така че, ако функцията е непрекъсната, тогава, когато нарастването на аргумента клони към нула, нарастването на функцията клони към нула. Те казват друго: малко увеличение на аргумента съответства на малко увеличение на функцията. На фиг. 3 е показана графика на непрекъсната в точка функция, нарастването съответства на нарастването на функцията. На фиг. 4 нарастване съответства на такова нарастване на функцията, което, колкото и малко да е, няма да бъде по-малко от половината от дължината на отсечката; функцията е прекъсната в точката .

Нашата идея за непрекъсната функция като функция, чиято графика може да бъде начертана, без да се вдига моливът от хартията, е перфектно подкрепена от свойствата на непрекъснатите функции, които са доказани в смятането. Нека отбележим например техните свойства.

1. Ако функция, която е непрекъсната на сегмент, приема стойности на различни знаци в краищата на сегмента, тогава в дадена точка от този сегмент тя приема стойност, равна на нула.

2. Функцията, непрекъсната на сегмента, приема всички междинни стойности между стойностите в крайните точки, т.е. между и .

3. Ако една функция е непрекъсната на отсечка, то на тази отсечка тя достига максималната и минималната си стойности, т.е. ако - най-малките и - най-големите стойности на функцията на сегмента , тогава има точки на този сегмент и , така че и .

Геометричният смисъл на първото от тези твърдения е съвсем ясен: ако непрекъсната крива минава от едната страна на оста към другата, тогава тя пресича тази ос (фиг. 5). Прекъснатата функция няма това свойство, което се потвърждава от графиката на функцията на фиг. 2, както и свойства 2 и 3. На фиг. 2 функция не приема стойността, въпреки че е оградена между и. На фиг. 6 показва пример за прекъсната функция (дробната част на числото), която не достига максималната си стойност.

Събирането, изваждането, умножението на непрекъснати функции на една и съща отсечка отново водят до непрекъснати функции. При разделянето на две непрекъснати функции се получава непрекъсната функция, ако знаменателят е различен от нула навсякъде.

Математиката стига до концепцията за непрекъсната функция, като изучава преди всичко различни закони на движение. Пространството и времето са непрекъснати и зависимостта например на пътя от времето, изразена от закона, дава пример за непрекъсната функция.

Непрекъснатите функции описват състояния и процеси в твърди вещества, течности и газове. Науките, които ги изучават - теорията на еластичността, хидродинамиката и аеродинамиката - са обединени от едно име - "механика на непрекъснатата среда".

В този урок ще научим как да установим непрекъснатостта на функция. Ще направим това с помощта на граници, освен това едностранни - дясно и ляво, които изобщо не са страшни, въпреки факта, че са написани като и .

Но какво е непрекъснатостта на една функция като цяло? Докато стигнем до стриктна дефиниция, най-лесният начин да си представим линия, която може да бъде начертана, без да вдигате молива от хартията. Ако се начертае такава линия, значи тя е непрекъсната. Тази линия е графиката на непрекъсната функция.

Графично една функция е непрекъсната в дадена точка, ако нейната графика не се "счупва" в тази точка. Графиката на такава непрекъсната функция е показано на фигурата по-долу.

Дефиниция на непрекъснатостта на функция през границата.Една функция е непрекъсната в точка при три условия:

1. Функцията е дефинирана в точката .

Ако поне едно от горните условия не е изпълнено, функцията не е непрекъсната в точка. В същото време те казват, че функцията претърпява прекъсване, а точките на графиката, в които графиката се прекъсва, се наричат ​​точки на прекъсване на функцията. Графиката на такава функция, която претърпява прекъсване в точката x=2, е показана на фигурата по-долу.

Пример 1функция f(х) се определя, както следва:

Ще бъде ли тази функция непрекъсната във всяка от граничните точки на нейните клонове, т.е. в точките х = 0 , х = 1 , х = 3 ?

Решение. Проверяваме и трите условия за непрекъснатост на функцията във всяка гранична точка. Първото условие е изпълнено, защото дефинирана функциявъв всяка от граничните точки следва от определението на функцията. Остава да проверим останалите две условия.

Точка х= 0 . Намерете лявата граница в тази точка:

.

Нека намерим дясната граница:

х= 0 трябва да се намери в разклонението на функцията, което включва тази точка, тоест второто разклонение. Намираме ги:

Както можете да видите, границата на функцията и стойността на функцията в точката х= 0 са равни. Следователно функцията е непрекъсната в точката х = 0 .

Точка х= 1. Намерете лявата граница в тази точка:

Нека намерим дясната граница:

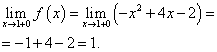
Функционална граница и функционална стойност в точка х= 1 трябва да се намери в разклонението на функцията, което включва тази точка, тоест второто разклонение. Намираме ги:

.

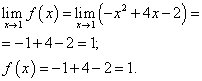Функционална граница и функционална стойност в точка х= 1 са равни. Следователно функцията е непрекъсната в точката х = 1 .

Точка х= 3 . Намерете лявата граница в тази точка:

Нека намерим дясната граница:

Функционална граница и функционална стойност в точка х= 3 трябва да се намери в разклонението на функцията, което включва тази точка, тоест второто разклонение. Намираме ги:

.

Функционална граница и функционална стойност в точка х= 3 са равни. Следователно функцията е непрекъсната в точката х = 3 .

Основен извод: тази функция е непрекъсната във всяка гранична точка.

Установете сами непрекъснатостта на функция в дадена точка и след това вижте решението

Непрекъсната промяна във функция може да се определи като промяна, която е постепенна, без скокове, при която малка промяна в аргумента води до малка промяна във функцията.

Нека илюстрираме тази непрекъсната промяна на функцията с пример.

Нека товар виси на конец над масата. Под действието на това натоварване нишката се разтяга, така че разстоянието лнатоварването от точката на окачване на нишката е функция от масата на товара м, това е л = f(м) , м≥0 .

Ако леко променим масата на товара, тогава разстоянието лмалка промяна: малка промяна мотговарят на малки промени л. Въпреки това, ако масата на товара е близка до якостта на опън на нишката, тогава малко увеличение на масата на товара може да доведе до скъсване на нишката: разстоянието лще се увеличи рязко и ще стане равно на разстоянието от точката на окачване до повърхността на масата. Функционална графика л = f(м) показано на фигурата. На сайта тази графика е непрекъсната (плътна) линия и в точката е прекъсната. Резултатът е графика, състояща се от два клона. Във всички точки с изключение на функцията л = f(м) е непрекъсната и в даден момент има прекъсване.

Изследването на функция за непрекъснатост може да бъде както самостоятелна задача, така и един от етапите на цялостно изследване на функцията и изграждането на нейната графика.

Непрекъснатост на функция на интервал

Нека функцията г = f(х) определен в интервала] а, b[ и е непрекъсната във всяка точка от този интервал. Тогава се нарича непрекъснат в интервала ] а, b[ . Концепцията за непрекъснатост на функция върху интервали от формата ]- ∞ се дефинира по подобен начин, b[ , ]а, + ∞[ , ]- ∞, + ∞[ . Сега нека функцията г = f(х) дефиниран на сегмента [ а, b] . Разликата между интервал и сегмент е, че граничните точки на интервала не са включени в интервала, но граничните точки на сегмента са включени в сегмента. Тук трябва да споменем така наречената едностранна приемственост: в точката а, оставайки на интервала [ а, b] , можем да подходим само отдясно и по същество b- само отляво. Функцията се нарича непрекъсната на интервала [ а, b] , ако е непрекъснат във всички вътрешни точки на този сегмент, непрекъснат отдясно в точката аи ляво непрекъснато в точката b.

Всяка от елементарните функции може да служи като пример за непрекъсната функция. Всяка елементарна функция е непрекъсната на всеки сегмент, на който е дефинирана. Например функциите и са непрекъснати на всеки интервал [ а, b] функцията е непрекъсната на сегмента [ 0 , b] , функцията е непрекъсната на всеки сегмент, който не съдържа точка а = 2 .

Пример 4Проучете функцията за непрекъснатост.

Решение. Нека проверим първото условие. Функцията не е дефинирана в точки - 3 и 3. Не е изпълнено поне едно от условията за непрекъснатост на функцията върху цялата числова ос. Следователно тази функция е непрекъсната на интервалите

Пример 5Определете при каква стойност на параметъра анепрекъснато през цялото време домейнифункция

Решение.

Нека намерим дясната граница за:

.

Очевидно е, че стойността в точката х= 2 трябва да е равно брадва :

а = 1,5 .

Пример 6Определете при какви стойности на параметрите аи bнепрекъснато през цялото време домейнифункция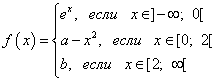

Решение.
Намерете лявата граница на функцията в точката:

.

Следователно стойността в точката трябва да е равна на 1:

Нека намерим лявата функция в точката:

Очевидно стойността на функцията в точката трябва да бъде равна на:

Отговор: функцията е непрекъсната в цялата област на дефиниция за а = 1; b = -3 .

Основни свойства на непрекъснатите функции

Математиката стига до концепцията за непрекъсната функция, като изучава преди всичко различни закони на движение. Пространството и времето са безкрайни и като зависимости са пътища сот време T, изразена със закон с = f(T) , дава пример за непрекъсната функции f(T) . Температурата на нагрятата вода също се променя непрекъснато, тя също е непрекъсната функция на времето: T = f(T) .

В математическия анализ са доказани някои свойства на непрекъснатите функции. Представяме най-важните от тези свойства.

1. Ако функция, която е непрекъсната на интервал, приема стойности на различни знаци в краищата на интервала, тогава в дадена точка от този сегмент тя приема стойност, равна на нула. По-формално, това свойство е дадено в теорема, известна като първата теорема на Болцано-Коши.

2. Функция f(х), непрекъсната на интервала [ а, b], приема всички междинни стойности между стойностите в крайните точки, тоест между f(а) и f(b) . По-формално, това свойство е дадено в теорема, известна като втората теорема на Болцано-Коши.