McLaren decomposition. Proširenje funkcija u nizove stepena

Ako je funkcija f(x) ima na nekom intervalu koji sadrži tačku A, derivati ​​svih redova, onda se na njega može primijeniti Taylorova formula:

Gdje r n– takozvani preostali član ili ostatak serije, može se procijeniti pomoću Lagrangeove formule:

, gdje je broj x između X I A.

Ako za neku vrijednost x r n®0 at n®¥, tada se u granici Taylor formula pretvara u konvergentnu formulu za ovu vrijednost Taylor serija:

Dakle, funkcija f(x) može se proširiti u Taylorov niz u dotičnoj tački X, Ako:

1) ima derivate svih naloga;

2) konstruisani niz konvergira u ovoj tački.

At A=0 dobijamo niz pod nazivom blizu Maclaurina:

Primjer 1 f(x)= 2x.

Rješenje. Nađimo vrijednosti funkcije i njenih derivata na X=0

f(x) = 2x, f( 0) = 2 0 =1;

f¢(x) = 2x ln2, f¢( 0) = 2 0 ln2= ln2;

f¢¢(x) = 2x u 2 2, f¢¢( 0) = 2 0 ln 2 2= ln 2 2;

f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.

Zamjenom dobivenih vrijednosti derivacija u formulu Taylorovog reda, dobivamo:

Radijus konvergencije ove serije jednako beskonačnosti, stoga ovo proširenje vrijedi za -¥<x<+¥.

Primjer 2 X+4) za funkciju f(x)= e x.

Rješenje. Pronalaženje izvoda funkcije e x i njihove vrijednosti u tom trenutku X=-4.

f(x)= e x, f(-4) = e -4 ;

f¢(x)= e x, f¢(-4) = e -4 ;

f¢¢(x)= e x, f¢¢(-4) = e -4 ;

f(n)(x)= e x, f(n)( -4) = e -4 .

Prema tome, traženi Taylorov red funkcije ima oblik:

Ovo proširenje vrijedi i za -¥<x<+¥.

Primjer 3 . Proširite funkciju f(x)=ln x u nizu moći ( X- 1),

(tj. u Tejlorovom nizu u blizini tačke X=1).

Rješenje. Pronađite izvode ove funkcije.

Zamjenom ovih vrijednosti u formulu dobijamo željeni Taylorov niz:

Koristeći d'Alembertov test, možete provjeriti da li se niz konvergira kada

½ X- 1½<1. Действительно,

Niz konvergira ako je ½ X- 1½<1, т.е. при 0<x<2. При X=2 dobijamo promenljivi niz koji zadovoljava uslove Lajbnicovog kriterijuma. At X=0 funkcija nije definirana. Dakle, područje konvergencije Taylorovog reda je poluotvoreni interval (0;2).

Predstavimo ovako dobijene ekspanzije u Maclaurinov niz (tj. u blizini tačke X=0) za neke elementarne funkcije:

(2) ,

(3) ,

( zove se posljednja dekompozicija binomni niz)

Primjer 4 . Proširite funkciju u niz stepena

Rješenje. U proširenju (1) zamjenjujemo X na – X 2, dobijamo:

Primjer 5 . Proširite funkciju u Maclaurin seriju

Rješenje. Imamo

Koristeći formulu (4), možemo napisati:

umjesto zamjene X u formulu -X, dobijamo:

Odavde nalazimo:

Otvaranjem zagrada, preuređivanjem termina serije i dovođenjem sličnih pojmova, dobijamo

Ovaj niz konvergira u intervalu

(-1;1), budući da se dobija iz dva niza, od kojih svaki konvergira u ovom intervalu.

Komentar .

Formule (1)-(5) se također mogu koristiti za proširenje odgovarajućih funkcija u Taylorov niz, tj. za proširenje funkcija u pozitivnim cijelim potencijama ( Ha). Da biste to učinili, potrebno je izvršiti takve identične transformacije na datoj funkciji kako bi se dobila jedna od funkcija (1)-(5), u kojoj umjesto X košta k( Ha) m , gdje je k konstantan broj, m je pozitivan cijeli broj. Često je zgodno napraviti promjenu varijable t=Ha i proširi rezultujuću funkciju u odnosu na t u Maclaurinovom nizu.

Ova metoda ilustruje teoremu o jedinstvenosti proširenja funkcije u niz stepena. Suština ove teoreme je da se u okolini iste tačke ne mogu dobiti dva različita niza stepena koji bi konvergirali istoj funkciji, bez obzira na to kako se vrši njeno proširenje.

Primjer 6 . Proširite funkciju u Taylorov niz u susjedstvu tačke X=3.

Rješenje. Ovaj se problem može riješiti, kao i prije, korištenjem definicije Taylorovog reda, za koji trebamo pronaći derivacije funkcije i njihove vrijednosti na X=3. Međutim, bit će lakše koristiti postojeće proširenje (5):

Rezultirajući niz konvergira na ili –3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

Primjer 7 . Napišite Taylorov niz u potencijama ( X-1) funkcije .

Rješenje.

Serija se konvergira na , ili -2< x£5.

Među funkcionalnim serijama najvažnije mjesto zauzimaju power serije.

Serija moći je serija

čiji su članovi funkcije stepena raspoređene u rastućim nenegativnim cijelim potencijama x, A c0 , c 1 , c 2 , c n - konstantne vrijednosti. Brojevi c1 , c 2 , c n - koeficijenti članova serije, c0 - besplatan član. Članovi stepena niza definisani su na cijeloj brojevnoj pravoj.

Hajde da se upoznamo sa konceptom područja konvergencije redova stepena. Ovo je skup vrijednosti varijable x, za koju se niz konvergira. Redovi snaga imaju prilično jednostavnu oblast konvergencije. Za stvarne vrijednosti varijabli x područje konvergencije se sastoji ili od jedne tačke, ili je određeni interval (interval konvergencije), ili se poklapa sa cijelom osom Ox .

Prilikom zamjene vrijednosti u niz stepena x= 0 će rezultirati nizom brojeva

c0 +0+0+...+0+... ,

koji konvergira.

Stoga, kada x= 0 bilo koji niz stepena konvergira i, prema tome, njeno područje konvergencije ne može biti prazan skup. Struktura oblasti konvergencije svih redova stepena je ista. Može se utvrditi korištenjem sljedeće teoreme.

Teorema 1 (Abelova teorema). Ako niz stepena konvergira na nekoj vrijednosti x = x 0 , različito od nule, onda konvergira, i, štaviše, apsolutno, za sve vrijednosti |x| < |x 0 | . Imajte na umu: i početna vrijednost “X je nula” i bilo koja vrijednost “X” koja se upoređuje sa početnom vrijednošću uzimaju se po modulu - bez uzimanja u obzir predznaka.

Posljedica. Ako redovi snaga divergiraju po nekoj vrijednosti x = x 1 , tada se divergira za sve vrijednosti |x| > |x 1 | .

Kao što smo već ranije saznali, bilo koji niz stepena konvergira na vrijednost x= 0. Postoje redovi stepena koji konvergiraju samo kada x= 0 i divergiraju za druge vrijednosti X. Izuzimajući ovaj slučaj iz razmatranja, pretpostavljamo da niz stepena konvergira na nekoj vrijednosti x = x 0 , različito od nule. Tada, prema Abelovom teoremu, konvergira u svim tačkama intervala ]-| x0 |, |x 0 |[ (interval čije su lijeva i desna granica x vrijednosti na kojima konvergira niz stepena, uzet sa predznakom minus i znakom plus, respektivno), simetričan u odnosu na ishodište.

Ako se niz stepena divergira na određenoj vrijednosti x = x 1 , onda, na osnovu posledica Abelove teoreme, divergira u svim tačkama izvan segmenta [-| x1 |, |x 1 |] . Iz toga slijedi da za bilo koji niz stepena postoji interval simetričan u odnosu na ishodište, tzv interval konvergencije , u svakoj tački u kojoj se niz konvergira, na granicama može konvergirati, ili može divergirati, i to ne nužno u isto vrijeme, a izvan segmenta niz divergira. Broj R naziva se radijus konvergencije niza stepena.

U posebnim slučajevima interval konvergencije stepena niza može degenerisati do tačke (tada se niz konvergira samo kada x= 0 i smatra se da je R= 0) ili predstavljaju cijelu brojevnu pravu (tada niz konvergira u svim tačkama brojevne prave i pretpostavlja se da je ).

Dakle, određivanje područja konvergencije stepena niza se sastoji u određivanju njegovog radijus konvergencije R i proučavanje konvergencije niza na granicama intervala konvergencije (na ).

Teorema 2. Ako su svi koeficijenti niza stepena, počevši od određenog, različiti od nule, tada je njegov polumjer konvergencije jednak granici u omjeru apsolutnih vrijednosti koeficijenata zajedničkih sljedećih članova niza , tj.

Primjer 1. Naći područje konvergencije stepena reda

Rješenje. Evo

Koristeći formulu (28), nalazimo radijus konvergencije ovog niza:

Proučimo konvergenciju niza na krajevima intervala konvergencije. Primjer 13 pokazuje da ovaj niz konvergira na x= 1 i divergira na x= -1. Prema tome, područje konvergencije je poluinterval.

Primjer 2. Naći područje konvergencije stepena reda

Rješenje. Koeficijenti serije su pozitivni, i

Nađimo granicu ovog omjera, tj. radijus konvergencije niza stepena:

Proučimo konvergenciju niza na krajevima intervala. Zamjena vrijednosti x= -1/5 i x= 1/5 u ovom redu daje:

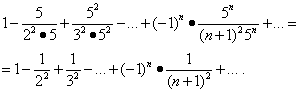
Prvi od ovih nizova konvergira (vidi primjer 5). Ali tada, na osnovu teoreme u odeljku „Apsolutna konvergencija“, drugi niz takođe konvergira, a područje njegove konvergencije je segment

Primjer 3. Naći područje konvergencije stepena reda

Rješenje. Evo

Koristeći formulu (28) nalazimo radijus konvergencije niza:

Proučimo konvergenciju serije za vrijednosti . Zamjenjujući ih u ovoj seriji, dobivamo respektivno

Oba niza divergiraju jer nužni uslov za konvergenciju nije zadovoljen (njihovi zajednički članovi ne teže nuli na ). Dakle, na oba kraja intervala konvergencije, ovaj niz divergira, a područje njegove konvergencije je interval.

Primjer 5. Naći područje konvergencije stepena reda

Rješenje. Nalazimo odnos gdje , i :

Prema formuli (28), radijus konvergencije ovog niza

,

odnosno, niz konvergira samo kada x= 0 i divergira za druge vrijednosti X.

Primjeri pokazuju da se na krajevima intervala konvergencije nizovi ponašaju drugačije. U primjeru 1, na jednom kraju intervala konvergencije, niz konvergira, a na drugom, u primjeru 2, konvergira na oba kraja;

Formula za radijus konvergencije stepena niza se dobija pod pretpostavkom da su svi koeficijenti članova reda, počevši od određene tačke, različiti od nule. Stoga je upotreba formule (28) dopuštena samo u ovim slučajevima. Ako je ovaj uvjet prekršen, tada treba tražiti radijus konvergencije niza stepena d'Alambertov znak, ili, zamjenom varijable, transformacijom niza u oblik u kojem je specificirani uvjet zadovoljen.

Primjer 6. Naći interval konvergencije stepena reda

Rješenje. Ova serija ne sadrži članove sa neparnim stepenima X. Stoga transformiramo seriju, postavljajući . Onda dobijamo seriju

da bismo pronašli polumjer konvergencije za koji možemo primijeniti formulu (28). Budući da je , a , tada je radijus konvergencije ove serije

Iz jednakosti dobivamo , Dakle, ovaj niz konvergira na intervalu .

Zbir potencijskog reda. Diferencijacija i integracija redova stepena

Neka za potencijski niz

radijus konvergencije R> 0, tj. ovaj niz konvergira na intervalu .

Zatim svaka vrijednost X iz intervala konvergencije odgovara određenom zbiru niza. Prema tome, zbir stepena reda je funkcija od X na intervalu konvergencije. Označavajući to sa f(x), možemo napisati jednakost

shvatajući to u smislu da je zbir niza u svakoj tački X iz intervala konvergencije jednak je vrijednosti funkcije f(x) u ovom trenutku. U istom smislu, reći ćemo da niz stepena (29) konvergira funkciji f(x) na intervalu konvergencije.

Izvan intervala konvergencije, jednakost (30) nema smisla.

Primjer 7. Nađi zbir stepena reda

Rješenje. Ovo je geometrijska serija za koju a= 1, a q= x. Stoga je njegov zbir funkcija . Niz konvergira ako , i je njegov interval konvergencije. Stoga jednakost

vrijedi samo za vrijednosti, iako je funkcija definisano za sve vrednosti X, osim X= 1.

Može se dokazati da je zbir stepena reda f(x) je kontinuiran i diferenciran na bilo kojem intervalu unutar intervala konvergencije, posebno u bilo kojoj tački u intervalu konvergencije niza.

Predstavimo teoreme o diferencijaciji po članu i integraciji stepena redova.

Teorema 1. Redovi stepena (30) u intervalu njegove konvergencije mogu se diferencirati pojam po član neograničen broj puta, a rezultirajući redovi stepena imaju isti radijus konvergencije kao i originalni niz, a njihovi sumi su respektivno jednaki .

Teorema 2. Redovi snaga (30) mogu se integrisati pojam po član neograničen broj puta u rasponu od 0 do X, ako , i rezultirajući niz stepena imaju isti radijus konvergencije kao i originalni niz, a njihovi zbroji su shodno tome jednaki

Proširenje funkcija u nizove stepena

Neka je funkcija data f(x), koji je potrebno proširiti u niz stepena, tj. predstaviti u obliku (30):

Zadatak je odrediti koeficijente red (30). Da bismo to učinili, diferencirajući jednakost (30) pojam po član, dosljedno nalazimo:

……………………………………………….. (31)

Uz pretpostavku jednakosti (30) i (31) X= 0, nalazimo

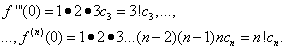
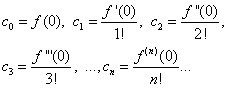
Zamjenom pronađenih izraza u jednakost (30) dobijamo

(32)

Nađimo ekspanziju nekih elementarnih funkcija u Maclaurinov red.

Primjer 8. Proširite funkciju u Maclaurin seriju

Rješenje. Derivati ​​ove funkcije se poklapaju sa samom funkcijom:

Stoga, kada X= 0 imamo

Zamjenom ovih vrijednosti u formulu (32) dobijamo željenu ekspanziju:

(33)

Ovaj niz konvergira na cijeloj brojevnoj pravoj (njegov radijus konvergencije).

16.1. Proširivanje elementarnih funkcija u Taylorov red i

Maclaurin

Pokažimo da ako je na skupu definirana proizvoljna funkcija
, u blizini tačke
ima mnogo izvoda i zbir je niza stepena:

tada možete pronaći koeficijente ove serije.

Zamijenimo u nizu po stepenu
. Onda
.

Nađimo prvi izvod funkcije
:

At
:
.

Za drugi izvod dobijamo:

At
:
.

Nastavak ove procedure n kada dobijemo:
.

Tako smo dobili niz stepena oblika:

,

koji se zove pored Taylora za funkciju
u blizini tačke
.

Poseban slučaj Taylorove serije je Maclaurin serija at
:

Ostatak Taylor (Maclaurin) serije se dobija odbacivanjem glavne serije n prvi članovi i označava se kao
. Zatim funkcija
može se napisati kao zbir n prvi članovi serije
i ostatak
:,

.

Ostatak je obično
izraženo različitim formulama.

Jedan od njih je u Lagrangeovom obliku:

, Gdje
.
.

Imajte na umu da se u praksi češće koristi Maclaurin serija. Dakle, da bi se zapisala funkcija
u obliku zbroja potencijskog reda potrebno je:

1) naći koeficijente Maclaurin (Taylor) reda;

2) naći oblast konvergencije rezultujućeg niza stepena;

3) dokazati da ovaj niz konvergira funkciji
.

Teorema1 (neophodan i dovoljan uslov za konvergenciju Maclaurinovog reda). Neka je radijus konvergencije serije
. Da bi se ovaj niz konvergirao u intervalu
da funkcioniše
, potrebno je i dovoljno da bi uslov bio zadovoljen:
u navedenom intervalu.

Teorema 2. Ako su derivati ​​bilo kojeg reda funkcije
u nekom intervalu
ograničen u apsolutnoj vrijednosti na isti broj M, odnosno
, zatim u ovom intervalu funkcija
može se proširiti u Maclaurin seriju.

Primjer1 . Proširite u Taylorov niz oko tačke
funkcija.

Rješenje.

.

,;

,
;

,
;

,

.......................................................................................................................................

,
;

Region konvergencije
.

Primjer2 . Proširite funkciju u Taylorovoj seriji oko tačke
.

Rješenje:

Nađite vrijednost funkcije i njenih derivata u
.

,
;

,
;

...........……………………………

,
.

Stavimo ove vrijednosti u red. dobijamo:

ili
.

Nađimo područje konvergencije ovog niza. Prema d'Alembertovom testu, niz konvergira ako

.

Stoga, za bilo koje ova granica je manja od 1 i stoga će raspon konvergencije niza biti:
.

Razmotrimo nekoliko primjera proširenja osnovnih elementarnih funkcija u Maclaurinov red. Podsjetimo da je Maclaurin serija:

.

konvergira na intervalu
da funkcioniše
.

Imajte na umu da je za proširenje funkcije u niz potrebno:

a) pronaći koeficijente Maclaurinovog reda za ovu funkciju;

b) izračunati radijus konvergencije za rezultirajući niz;

c) dokazati da rezultirajući niz konvergira funkciji
.

Primjer 3. Razmotrite funkciju
.

Rješenje.

Izračunajmo vrijednost funkcije i njenih derivata na
.

Tada numerički koeficijenti serije imaju oblik:

za bilo koga n. Zamenimo pronađene koeficijente u Maclaurinov niz i dobijemo:

Nađimo radijus konvergencije rezultirajućeg niza, i to:

.

Dakle, niz konvergira na intervalu
.

Ovaj niz konvergira funkciji za bilo koje vrednosti , jer na bilo kojem intervalu
funkcija a njeni derivati ​​apsolutne vrijednosti su ograničeni u broju .

Primjer4 . Razmotrite funkciju
.

Rješenje.

:

Lako je vidjeti da su derivati ​​parnog reda
, a derivati ​​su neparnog reda. Zamenimo pronađene koeficijente u Maclaurinov red i dobijemo ekspanziju:

Nađimo interval konvergencije ovog niza. Prema d'Alambertovom znaku:

za bilo koga . Dakle, niz konvergira na intervalu
.

Ovaj niz konvergira funkciji
, jer su svi njegovi derivati ​​ograničeni na jedinstvo.

Primjer5 .
.

Rješenje.

Nađimo vrijednost funkcije i njenih derivata na
:

Dakle, koeficijenti ove serije:
I
, dakle:

Slično kao u prethodnom redu, područje konvergencije
. Serija konvergira funkciji
, jer su svi njegovi derivati ​​ograničeni na jedinstvo.

Imajte na umu da je funkcija
neparna i serijska ekspanzija po neparnim stepenima, funkcija
– čak i širenje u niz u parnim snagama.

Primjer6 . Binomni niz:
.

Rješenje.

Nađimo vrijednost funkcije i njenih derivata na
:

Iz ovoga se vidi da:

Zamijenimo ove vrijednosti koeficijenata u Maclaurinov red i dobijemo proširenje ove funkcije u niz stepena:

Nađimo radijus konvergencije ovog niza:

Dakle, niz konvergira na intervalu
. Na graničnim tačkama na
I
niz može ili ne mora konvergirati ovisno o eksponentu
.

Proučeni niz konvergira na intervalu
da funkcioniše
, odnosno zbir serije
at
.

Primjer7 . Proširimo funkciju u Maclaurinovom nizu
.

Rješenje.

Da proširimo ovu funkciju u niz, koristimo binomni niz at
. dobijamo:

Na osnovu svojstva redova stepena (redovi stepena se mogu integrisati u oblast njegove konvergencije), nalazimo integral leve i desne strane ovog niza:

Nađimo područje konvergencije ove serije:
,

odnosno područje konvergencije ove serije je interval
.

Odredimo konvergenciju niza na krajevima intervala. At
. Ova serija je harmonična serija, odnosno razilazi se. At
.

dobijamo niz brojeva sa zajedničkim pojmom
.

Niz konvergira prema Leibnizovom testu. Dakle, područje konvergencije ovog niza je interval

16.2. Primena redova stepena u približnim proračunima n U približnim proračunima, redovi snaga igraju izuzetno važnu ulogu. Uz njihovu pomoć sastavljene su tablice trigonometrijskih funkcija, tablice logaritama, tablice vrijednosti drugih funkcija koje se koriste u različitim područjima znanja, na primjer, u teoriji vjerojatnosti i matematičkoj statistici. Osim toga, proširenje funkcija u niz stepena korisno je za njihovo teorijsko proučavanje. Glavni problem pri korištenju niza stepena u približnim proračunima je pitanje procjene greške pri zamjeni sume niza zbirom njegovih prvih

članovi.

Razmotrimo dva slučaja:

funkcija se proširuje u naizmjeničnu seriju;

funkcija je proširena u niz znakova konstante.

Proračun korištenjem naizmjeničnih serija
Neka funkcija proširen u niz naizmjeničnih snaga. Zatim prilikom izračunavanja ove funkcije za određenu vrijednost n dobijamo niz brojeva na koji možemo primijeniti Leibnizov kriterij. U skladu s ovim kriterijem, ako se zbir niza zamijeni zbirom njegovog prvog
.

Primjer8 . članova, tada apsolutna greška ne prelazi prvi član ostatka ovog niza, to jest:
Izračunaj

Rješenje.

sa tačnošću od 0,0001.
Koristit ćemo Maclaurin seriju za

Ako uporedimo prvi i drugi član serije sa datom tačnošću, onda: .

Treći termin proširenja:

manja od navedene tačnosti proračuna. Stoga, da izračunate
dovoljno je ostaviti dva člana serije, tj

.

Dakle
.

Primjer9 . članova, tada apsolutna greška ne prelazi prvi član ostatka ovog niza, to jest:
sa tačnošću od 0,001.

Rješenje.

Koristićemo formulu binomnog niza. Da bismo to uradili, pišimo
u obliku:
.

U ovom izrazu
,

Uporedimo svaki od pojmova serije sa tačnošću koja je navedena. To je jasno
. Stoga, da izračunate
dovoljno je ostaviti tri termina serije.

ili
.

Proračun korištenjem pozitivnih serija

Primjer10 . Izračunaj broj sa tačnošću od 0,001.

Rješenje.

U nizu za funkciju
hajde da zamenimo
. dobijamo:

Procijenimo grešku koja nastaje pri zamjeni sume niza zbirom prvog članovi. Zapišimo očiglednu nejednakost:

to je 2<<3. Используем формулу остаточного члена ряда в форме Лагранжа:
,
.

Prema problemu, morate pronaći n tako da vrijedi sljedeća nejednakost:
ili
.

Lako je to provjeriti kada n= 6:
.

dakle,
.

Primjer11 . članova, tada apsolutna greška ne prelazi prvi član ostatka ovog niza, to jest:
sa tačnošću od 0,0001.

Rješenje.

Imajte na umu da se za izračunavanje logaritma može koristiti niz za funkciju
, ali ovaj niz konvergira veoma sporo i da bi se postigla zadata tačnost bilo bi potrebno uzeti 9999 članova! Stoga se za izračunavanje logaritama u pravilu koristi niz za funkciju
, koji konvergira na intervalu
.

Hajde da izračunamo
koristeći ovu seriju. Neka
, Onda .

dakle,
,

Da bi izračunali
sa datom tačnošću, uzmi zbir prva četiri člana:
.

Ostatak serije
hajde da ga odbacimo. Procijenimo grešku. Očigledno je da

ili
.

Tako je u nizu koji je korišten za izračunavanje bilo dovoljno uzeti samo prva četiri člana umjesto 9999 u nizu za funkciju
.

Pitanja za samodijagnozu

1. Šta je Taylor serija?

2. Kakav je oblik imao Maclaurinov niz?

3. Formulirajte teoremu o proširenju funkcije u Taylorov red.

4. Zapišite proširenje glavnih funkcija Maclaurinove serije.

5. Navedite područja konvergencije razmatranih serija.

6. Kako procijeniti grešku u aproksimativnim proračunima pomoću nizova stepena?

Proširenje funkcije u serije Taylor, Maclaurin i Laurent na mjestu za obuku praktičnih vještina. Ovo proširenje funkcije u niz omogućava matematičarima da procijene približnu vrijednost funkcije u nekom trenutku u njenom domenu definicije. Mnogo je lakše izračunati takvu vrijednost funkcije u odnosu na korištenje Bredisove tablice, koja je toliko nebitna u doba kompjuterske tehnologije. Proširiti funkciju u Taylorov red znači izračunati koeficijente linearnih funkcija ovog niza i napisati je u ispravnom obliku. Učenici brkaju ova dva niza, ne shvatajući šta je opšti slučaj, a šta poseban slučaj drugog. Podsjetimo jednom za svagda Maclaurinov red je poseban slučaj Taylorovog reda, odnosno ovo je Taylorov red, ali u tački x = 0. Svi kratki unosi za proširenje dobro poznatih funkcija, kao što su e^x, Sin(x), Cos(x) i drugi, ovo su proširenja Taylorovog reda, ali u tački 0 za argument. Za funkcije složenog argumenta, Lorentov red je najčešći problem u TFCT-u, budući da predstavlja dvostrani beskonačan niz. To je zbir dvije serije. Predlažemo da pogledate primjer dekompozicije direktno na web stranici, to je vrlo lako učiniti klikom na “Primjer” s bilo kojim brojem, a zatim na dugme “Rješenje”. Upravo je ovo proširenje funkcije u niz koji je povezan s majorizirajućim nizom koji ograničava izvornu funkciju u određenom području duž ordinatne ose ako varijabla pripada području apscise. Vektorska analiza uspoređuje se s još jednom zanimljivom disciplinom u matematici. Budući da svaki termin treba ispitati, proces zahtijeva dosta vremena. Bilo koji Taylorov niz može biti povezan s Maclaurinovim nizom zamjenom x0 sa nulom, ali za Maclaurinov niz ponekad nije očigledno da se Taylorov red predstavlja obrnuto. Kao da se to ne traži u čistom obliku, zanimljivo je za opći samorazvoj. Svaki Laurentov niz odgovara dvostranom beskonačnom nizu stepena u cijelim potencijama z-a, drugim riječima, nizu istog Taylorovog tipa, ali malo drugačijem u izračunavanju koeficijenata. O području konvergencije Laurentove serije ćemo govoriti nešto kasnije, nakon nekoliko teorijskih proračuna. Kao iu prošlom veku, postepeno proširenje funkcije u niz teško se može postići jednostavnim dovođenjem članova na zajednički nazivnik, jer su funkcije u nazivnicima nelinearne. Formulacija problema zahtijeva približan proračun funkcionalne vrijednosti. Razmislite o činjenici da kada je argument Taylorovog reda linearna varijabla, tada se proširenje događa u nekoliko koraka, ali je slika potpuno drugačija kada je argument funkcije koja se proširuje složena ili nelinearna funkcija, tada se proces predstavljanje takve funkcije u nizu stepena je očigledno, jer je na ovaj način lako izračunati, iako približnu vrijednost, u bilo kojoj tački u domeni definicije, uz minimalnu grešku koja ima mali utjecaj na daljnje proračune. Ovo važi i za Maclaurin seriju. kada je potrebno izračunati funkciju u nultoj tački. Međutim, sam Laurentov niz ovdje je predstavljen ekspanzijom na ravan sa imaginarnim jedinicama. Takođe, ispravno rješenje problema tokom cjelokupnog procesa neće biti bez uspjeha. Ovaj pristup nije poznat u matematici, ali objektivno postoji. Kao rezultat, možete doći do zaključka o takozvanim tačkastim podskupovima, a za proširenje funkcije u nizu morate koristiti metode poznate za ovaj proces, kao što je primjena teorije izvoda. Još jednom smo uvjereni da je nastavnik bio u pravu kada je iznio svoje pretpostavke o rezultatima postračunarskih proračuna. Napomenimo da Taylorov niz, dobijen po svim kanonima matematike, postoji i definiran je na cijeloj numeričkoj osi, međutim, poštovani korisnici servisa stranice, ne zaboravite tip originalne funkcije, jer može ispasti da je u početku potrebno uspostaviti domen definicije funkcije, odnosno napisati i isključiti iz daljeg razmatranja one tačke u kojima funkcija nije definirana u domeni realnih brojeva. Takoreći, ovo će pokazati vašu efikasnost u rješavanju problema. Konstrukcija Maclaurinove serije sa nultom vrednošću argumenta neće biti izuzetak od onoga što je rečeno. Proces pronalaženja domena definicije funkcije nije otkazan i ovoj matematičkoj operaciji morate pristupiti sa punom ozbiljnošću. U slučaju Laurentovog niza koji sadrži glavni dio, parametar "a" će se zvati izolirana singularna točka, a Laurentov niz će se proširiti u prsten - to je sjecište područja konvergencije njegovih dijelova, dakle slijedi odgovarajuća teorema. Ali nije sve tako komplikovano kao što se na prvi pogled čini neiskusnom studentu. Proučavajući Taylorov niz, lako možete razumjeti Laurentov niz - generalizirani slučaj za proširenje prostora brojeva. Bilo koje proširenje funkcije u niz može se izvesti samo u točki u domeni definicije funkcije. Svojstva funkcija kao što su periodičnost ili beskonačna diferencijabilnost treba uzeti u obzir. Također predlažemo da koristite tabelu gotovih proširenja elementarnih funkcija Taylorovog niza, budući da se jedna funkcija može predstaviti sa do desetine različitih nizova stepena, što se može vidjeti iz našeg online kalkulatora. Online Maclaurin seriju je lako odrediti, ako koristite jedinstvenu uslugu web stranice, samo trebate unijeti ispravnu napisanu funkciju i dobit ćete predstavljeni odgovor za nekoliko sekundi, garantirano je tačan i u standardni pisani oblik. Rezultat možete kopirati direktno u čistu kopiju za predaju nastavniku. Bilo bi ispravno prvo odrediti analitičnost dotične funkcije u prstenovima, a zatim nedvosmisleno reći da je ona proširiva u Lorentov red u svim takvim prstenovima. Važno je ne izgubiti iz vida pojmove Lorentove serije koji sadrže negativne moći. Fokusirajte se na ovo što je više moguće. Dobro iskoristite Laurentov teorem o proširenju funkcije u cjelobrojne stepene.

Ako funkcija f(x) ima derivate svih redova na određenom intervalu koji sadrži tačku a, tada se na nju može primijeniti Taylorova formula:
,
Gdje r n– takozvani preostali član ili ostatak serije, može se procijeniti pomoću Lagrangeove formule:
, gdje je broj x između x i a.

Pravila za unos funkcija:

Ako za neku vrijednost X r n→0 at n→∞, tada u granici Taylor formula postaje konvergentna za ovu vrijednost Taylor serija:
,
Dakle, funkcija f(x) može se proširiti u Taylorov red u tački x koja se razmatra ako:
1) ima derivate svih naloga;
2) konstruisani niz konvergira u ovoj tački.

Kada je a = 0, dobijamo niz nazvan blizu Maclaurina:
,
Proširenje najjednostavnijih (elementarnih) funkcija u Maclaurin seriji:
Eksponencijalne funkcije
, R=∞
Trigonometrijske funkcije
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funkcija actgx se ne širi po stepenu x, jer ctg0=∞
Hiperboličke funkcije


Logaritamske funkcije
, -1
Binomni nizovi
.

Primjer br. 1. Proširite funkciju u niz stepena f(x)= 2x.
Rješenje. Nađimo vrijednosti funkcije i njenih derivata na X=0
f(x) = 2x, f( 0) = 2 0 =1;
f"(x) = 2x ln2, f"( 0) = 2 0 ln2= ln2;
f""(x) = 2x u 2 2, f""( 0) = 2 0 ln 2 2= ln 2 2;
…
f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.
Zamjenom dobijenih vrijednosti derivata u formulu Taylorovog reda, dobivamo:

Radijus konvergencije ovog niza jednak je beskonačnosti, stoga ovo proširenje vrijedi za -∞<x<+∞.

Primjer br. 2. Napišite Taylorov niz u potencijama ( X+4) za funkciju f(x)= e x.
Rješenje. Pronalaženje izvoda funkcije e x i njihove vrijednosti u tom trenutku X=-4.
f(x)= e x, f(-4) = e -4 ;
f"(x)= e x, f"(-4) = e -4 ;
f""(x)= e x, f""(-4) = e -4 ;
…
f(n)(x)= e x, f(n)( -4) = e -4 .
Prema tome, traženi Taylorov red funkcije ima oblik:

Ovo proširenje vrijedi i za -∞<x<+∞.

Primjer br. 3. Proširite funkciju f(x)=ln x u nizu moći ( X- 1),
(tj. u Tejlorovom nizu u blizini tačke X=1).
Rješenje. Pronađite izvode ove funkcije.
f(x)=lnx , , , ,

f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Zamjenom ovih vrijednosti u formulu dobijamo željeni Taylorov niz:

Koristeći d'Alembertov test, možete provjeriti da se niz konvergira na ½x-1½<1 . Действительно,

Niz konvergira ako je ½ X- 1½<1, т.е. при 0<x<2. При X=2 dobijamo naizmeničnu seriju koja zadovoljava uslove Lajbnicovog kriterijuma. Kada je x=0 funkcija nije definirana. Dakle, područje konvergencije Taylorovog reda je poluotvoreni interval (0;2).

Primjer br. 4. Proširite funkciju u niz stepena.
Rješenje. U proširenju (1) zamjenjujemo x sa -x 2, dobijamo:
, -∞

Primjer br. 5. Proširite funkciju u Maclaurin seriju.
Rješenje. Imamo
Koristeći formulu (4), možemo napisati:

zamjenom –x umjesto x u formuli, dobijamo:

Odavde nalazimo: ln(1+x)-ln(1-x) = -
Otvaranjem zagrada, preuređivanjem termina serije i dovođenjem sličnih pojmova, dobijamo
. Ovaj niz konvergira u intervalu (-1;1), jer se dobija iz dva niza, od kojih svaki konvergira u ovom intervalu.

Komentar .
Formule (1)-(5) se također mogu koristiti za proširenje odgovarajućih funkcija u Taylorov niz, tj. za proširenje funkcija u pozitivnim cijelim potencijama ( Ha). Da biste to učinili, potrebno je izvršiti takve identične transformacije na datoj funkciji kako bi se dobila jedna od funkcija (1)-(5), u kojoj umjesto X košta k( Ha) m , gdje je k konstantan broj, m je pozitivan cijeli broj. Često je zgodno napraviti promjenu varijable t=Ha i proširi rezultujuću funkciju u odnosu na t u Maclaurinovom nizu.

Ova metoda je zasnovana na teoremi o jedinstvenosti proširenja funkcije u niz stepena. Suština ove teoreme je da se u okolini iste tačke ne mogu dobiti dva različita niza stepena koji bi konvergirali istoj funkciji, bez obzira na to kako se vrši njeno proširenje.

Primjer br. 5a. Proširite funkciju u Maclaurinov niz i označite područje konvergencije.
Rješenje. Prvo nalazimo 1-x-6x 2 =(1-3x)(1+2x) , .
na osnovnu:

Razlomak 3/(1-3x) se može smatrati zbirom beskonačno opadajuće geometrijske progresije sa nazivnikom 3x, ako je |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

sa područjem konvergencije |x|< 1/3.

Primjer br. 6. Proširite funkciju u Taylorov red u blizini tačke x = 3.
Rješenje. Ovaj se problem može riješiti, kao i prije, korištenjem definicije Taylorovog reda, za koji trebamo pronaći derivacije funkcije i njihove vrijednosti na X=3. Međutim, bit će lakše koristiti postojeće proširenje (5):
=
Rezultirajući niz konvergira na ili –3

Primjer br. 7. Napišite Taylorov red po stepenu (x -1) funkcije ln(x+2) .
Rješenje.


Serija konvergira na , ili -2< x < 5.

Primjer br. 8. Proširite funkciju f(x)=sin(πx/4) u Taylorov red u blizini tačke x =2.
Rješenje. Napravimo zamjenu t=x-2:

Koristeći ekspanziju (3), u kojoj zamjenjujemo π / 4 t umjesto x, dobijamo:

Rezultirajući niz konvergira datoj funkciji na -∞< π / 4 t<+∞, т.е. при (-∞dakle,
, (-∞

Približni proračuni korištenjem nizova stepena

• ako je rezultirajući niz naizmjeničan, tada se koristi sljedeće svojstvo: za naizmjenični niz koji zadovoljava Leibnizove uslove, ostatak serije u apsolutnoj vrijednosti ne prelazi prvi odbačeni član.
• ako je dati niz konstantnog predznaka, tada se niz sastavljen od odbačenih članova upoređuje sa beskonačno opadajućom geometrijskom progresijom.
• u opštem slučaju, da biste procenili ostatak Taylorovog niza, možete koristiti Lagrangeovu formulu: a x ).

Primjer br. 1. Izračunajte ln(3) na najbliže 0,01.
Rješenje. Koristimo proširenje gdje je x=1/2 (vidi primjer 5 u prethodnoj temi):

Provjerimo da li možemo odbaciti ostatak nakon prva tri člana proširenja da bismo to učinili, procijenićemo ga koristeći zbir beskonačno opadajuće geometrijske progresije:

Tako da možemo odbaciti ovaj ostatak i dobiti

Primjer br. 2. Izračunajte na najbližih 0,0001.
Rješenje. Koristimo binomni niz. Budući da je 5 3 kocka cijelog broja najbliži 130, preporučljivo je broj 130 predstaviti kao 130 = 5 3 +5.



budući da je već četvrti član rezultirajućeg naizmjeničnog niza koji zadovoljava Leibnizov kriterij manji od tražene tačnosti:
, tako da se on i uslovi koji slijede mogu odbaciti.
Mnogi praktično potrebni određeni ili nepravilni integrali ne mogu se izračunati pomoću Newton-Leibnizove formule, jer je njena primjena povezana s pronalaženjem antiderivata, koji često nema izraz u elementarnim funkcijama. Dešava se i da je pronalaženje antiderivata moguće, ali je to nepotrebno radno intenzivno. Međutim, ako se funkcija integranda proširi u niz stepena, a granice integracije pripadaju intervalu konvergencije ovog niza, tada je moguće približno izračunavanje integrala sa unaprijed određenom tačnošću.

Primjer br. 3. Izračunajte integral ∫ 0 1 4 sin (x) x sa tačnošću od 10 -5.
Rješenje. Odgovarajući neodređeni integral ne može se izraziti u elementarnim funkcijama, tj. predstavlja “nestalni integral”. Ovdje se ne može primijeniti Newton-Leibnizova formula. Izračunajmo približno integral.
Dijeljenje pojma po pojmu niz za grijeh x on x, dobijamo:

Integrirajući ovaj niz član po član (ovo je moguće, budući da granice integracije pripadaju intervalu konvergencije ovog niza), dobijamo:

Pošto rezultujući niz zadovoljava Leibnizove uslove i dovoljno je uzeti zbir prva dva člana da bi se dobila željena vrednost sa datom tačnošću.
Dakle, nalazimo
.

Primjer br. 4. Izračunajte integral ∫ 0 1 4 e x 2 sa tačnošću od 0,001.
Rješenje.
. Provjerimo da li možemo odbaciti ostatak nakon drugog člana rezultirajućeg niza.
0,0001<0.001. Следовательно, .