Loranov niz izolovanih singularnih tačaka i njihova klasifikacija. Singularna tačka
Taylorovi redovi služe kao efikasan alat za proučavanje funkcija koje su analitičke u krugu zol Za proučavanje funkcija koje su analitične u domeni prstena, ispostavilo se da je moguće konstruirati ekspanzije u pozitivnim i negativnim potencijama (z - zq) oblika koje generaliziraju Taylorove ekspanzije. Niz (1), shvaćen kao zbir dva niza, naziva se Lorentov red. Jasno je da je područje konvergencije serije (1) zajednički dio područja konvergencije svakog od nizova (2). Hajde da je nađemo. Područje konvergencije prvog niza je kružnica čiji je polumjer određen Cauchy-Hadamardovom formulom Unutar kruga konvergencije, niz (3) konvergira na analitičku funkciju, au bilo kojoj kružnici manjeg radijusa konvergira. apsolutno i jednolično. Drugi red je power series u odnosu na varijablu, Serija (5) konvergira unutar svog kruga konvergencije na analitičku funkciju kompleksne varijable m-*oo, au bilo kojem krugu manjeg radijusa konvergira apsolutno i ravnomjerno, što znači da je područje konvergencije serije (4) je izvan kruga - Ako tada postoji zajednička površina konvergencije nizova (3) i (4) je kružni prsten u kojem niz (1) konvergira u analitičku funkciju. Štaviše, u bilo kojem prstenu se konvergira apsolutno i jednolično. Primjer 1. Odrediti područje konvergencije rad Laurentovog reda Izolirane singularne tačke i njihova klasifikacija M Područje konvergencije prvog niza je vanjski dio kruga, a područje konvergencije drugog niza je unutrašnjost kružnice Dakle, ovaj niz konvergira u krugove Teorema 15. Bilo koja funkcija f (z), jednoznačna i apolitična u kružnom prstenu može se u ovom prstenu predstaviti kao zbir konvergentnog niza, čiji su koeficijenti Cn jednoznačno određeni i izračunati prema formulama gdje je 7p kružnica polumjera m fiksirajmo proizvoljnu tačku z unutar prstena R. Konstruirajmo kružnice sa centrima u tački r, čiji polumjeri zadovoljavaju nejednakosti i razmotrimo novi prsten Koristeći Cauchyjevu integralnu teoremu za višestruko povezano područje, transformiramo zasebno svaki od integrala u zbiru (8). Za sve tačke £ duž kružnice 7d* zadovoljena je relacija de zbroja ravnomerno konvergentnog niza 1 1. Stoga se razlomak ^ može predstaviti u vi- / "/ množenjem oba dela kontinuiranom funkcijom (O i provođenjem). Integracijom po članu duž kružnice dobijamo da transformaciju drugog integrala izvodimo na nešto drugačiji način. Za sve tačke £ na kružnici ir> vrijedi sljedeća relacija kao zbir uniformno konvergentnog niza Množenjem oba dijela kontinuiranom funkcijom) i integrirajući polovično duž kružnice 7/, dobivamo da su integrandi u formulama (10) i (12) analitičke funkcije u kružnom prstenu. Prema tome, prema Cauchyjevom teoremu, vrijednosti odgovarajućih integrala neće se promijeniti ako krugove 7/r i 7r/ zamijenimo bilo kojim krugom desna strana formule (8) sa njihovim izrazima (9) i (11), respektivno, dobijamo traženo proširenje Kako je z proizvoljna tačka prstena, sledi da niz (14) konvergira funkciji f(. z) svuda u ovom prstenu, iu bilo kom prstenu, red konvergira ovoj funkciji apsolutno i ravnomerno. Dokažimo sada da je dekompozicija oblika (6) jedinstvena. Pretpostavimo da postoji još jedno proširenje. Tada ćemo svuda unutar prstena R imati na kružnici, nizovi (15) jednoliko konvergirani. Pomnožimo obje strane jednakosti (gdje je m fiksni cijeli broj i integrirajmo oba reda član po član. Kao rezultat dobijemo na lijevoj strani, a na desnoj - St. Dakle, (4, = St. m je proizvoljan broj, posljednja jednakost dokazuje jedinstvenost proširenja (6), čiji se koeficijenti izračunavaju pomoću formule (7), naziva se Lorentov red funkcije f(z). skup pojmova ove serije sa not negativne moći pozvao desni deo Laurent serija, a s negativnim - njen glavni dio. Formule (7) za koeficijente Laurentovog reda rijetko se koriste u praksi, jer po pravilu zahtijevaju glomazne proračune. Obično se, ako je moguće, koriste gotove Taylorove ekspanzije elementarnih funkcija. Na osnovu jedinstvenosti dekompozicije, svaka legalna metoda dovodi do istog rezultata. Primjer 2. Razmotrimo proširenja funkcija u Laurentov red u različitim područjima, uz pretpostavku da Fuiscia /(r) ima dvije singularne točke: . Prema tome, postoje tri prstenasta područja, sa centrom u tački r = 0. U svakom od njih funkcija /(r) je analitička: a) krug je prsten, spoljašnjost kružnice (slika 27). Nađimo Laurentove ekspanzije funkcije /(z) u svakoj od ovih regija. Predstavimo /(z) kao zbir elementarnih razlomaka a) Krug Relaciju (16) transformiramo na sljedeći način geometrijska progresija, dobijamo Zamenite pronađena proširenja u formulu (17): Ovo proširenje je Taylorov red funkcije /(z). b) Prsten za funkciju -r ostaje konvergentan u ovom prstenu, budući da red (19) za funkciju j^j za |z| > 1 se razilazi. Stoga transformiramo funkciju /(z) na sljedeći način: ponovo primjenom formule (19), dobijamo da ovaj niz konvergira za. Zamjenom proširenja (18) i (21) u relaciju (20) dobijamo c) Eksterijer kruga za funkciju -z za |z| > 2 divergira, a niz (21) za funk- Predstavimo funkciju /(z) u sljedećem obliku: /<*>Koristeći formule (18) i (19), dobijamo OR 1 Ovaj primjer pokazuje da za istu funkciju f(z) Laurentova ekspanzija, općenito govoreći, ima različite vrste za različite prstenove. Primjer 3. Pronađite proširenje 8. Laurentovog niza funkcije Laurentov red Izolirane singularne tačke i njihova klasifikacija u domenu prstena A Koristimo prikaz funkcije f(z) u sljedećem obliku: i transformiramo drugi član Koristeći formulu za zbir članova geometrijske progresije, dobijamo Zamjenom pronađenih izraza u formulu (22) imamo primjer 4. Proširimo u Lorentov red funkciju u blizini čeljusti zq = 0. Za bilo koji kompleks možemo ima Neka Ova ekspanzija vrijedi za bilo koju tačku z F 0. U ovom slučaju, područje prstena predstavlja cijelu kompleksnu ravan sa jednom odbačenom tačkom z - 0. Ovo područje se može definirati sljedećom relacijom: Ova funkcija je analitička u području Iz formula (13) za koeficijente Laurentovog reda, koristeći isto rezonovanje kao u prethodnom pasusu, mogu se dobiti Kouiwove nejednačine. ako je funkcija f(z) ograničena na kružnicu, gdje je M konstanta), tada Izolirane singularne točke Tačka zo se naziva izolirana singularna točka funkcije f(z) ako postoji prstenasto susjedstvo tačke ( ovaj skup se ponekad naziva probušenom okolinom tačke 2o), u kojoj je funkcija f(z) jedinstvena i analitična. U samoj tački zo, funkcija je ili nedefinirana ili nije jednoznačna i analitička. U zavisnosti od ponašanja funkcije /(r) pri približavanju tački zo, razlikuju se tri tipa singularnih tačaka. Za izoliranu singularnu točku kaže se da je: 1) uklonjiva ako postoji konačna 2) pymusach ako 3) suštinski singularna točka ako funkcija f(z) nema ograničenja na Tip izolirane singularne točke je usko povezan s priroda Laurentove ekspanzije funkcije po probušenom centru . Teorema 16. Izolovana singularna tačka z0 funkcije f(z) je uklonjiva singularna tačka ako i samo ako Laurentova ekspanzija funkcije f(z) u okolini tačke zo ne sadrži glavni dio, tj. ima oblik Neka je zo uklonjiva singularna tačka. Tada postoji konačna, dakle, funkcija f(z) je ograničena u prokološkoj okolini tačke z. Na osnovu Cauchyjevih nejednakosti postavljamo p. - 20) jednaki su nuli: Obrnuto, neka Loranova ekspanzija funkcije /(r) u susjedstvu tačke zq sadrži samo ispravan dio, odnosno ima oblik (23) i stoga je Taylor. Lako je vidjeti da za z -* z0 funkcija /(z) ima graničnu vrijednost: Teorema 17. Izolovana singularna tačka zq funkcije f(z) je uklonjiva ako i samo ako je funkcija J(z) omeđen u nekom probušenom okruženju tačke zq, Zgmechai nije. Neka je r uklonjiva singularna tačka funkcije /(r). Uz pretpostavku da je funkcija /(r) analitična u nekom krugu sa centrom u tački r. Ovo određuje naziv tačke - uklonjiv.
Modeli opisani sistemima dviju autonomnih diferencijalnih jednadžbi.
Fazna ravan. Fazni portret. Izoklin metoda. Glavne izokline. Održivost stabilno stanje. Linearni sistemi. Vrste singularnih tačaka: čvor, sedlo, fokus, centar. primjer: hemijske reakcije prva narudžba.
Najzanimljiviji rezultati o kvalitativnom modeliranju svojstava bioloških sistema dobijeni su korištenjem modela dvije diferencijalne jednadžbe koje omogućavaju kvalitativno istraživanje koristeći metodu fazna ravan. Razmotrimo sistem od dvije autonomne obične diferencijalne jednadžbe opšti pogled
(4.1)
P(x,y), Q(x,y)- kontinuirane funkcije, definisan u nekom području G Euklidska ravan ( x,y ‑ Kartezijanske koordinate) i imaju u ovoj regiji kontinuirane derivate reda ne nižeg od prvog.
Region G može biti neograničen ili ograničen. Ako su varijable x, y imaju specifično biološko značenje (koncentracije supstanci, broj vrsta) najčešće područje G predstavlja pozitivni kvadrant desne poluravnine:
0 £ x< ¥ ,0 £ y< ¥ .
Koncentracije tvari ili broj vrsta također se mogu ograničiti odozgo volumenom posude ili površinom staništa. Tada raspon vrijednosti varijabli ima oblik:
0 £ x< x 0 , 0 £ y< y 0 .
Varijable x, y promjena u vremenu u skladu sa sistemom jednadžbi (4.1), tako da svakom stanju sistema odgovara par vrijednosti varijabli ( x, y).
|
|
 |
Obrnuto, svaki par varijabli ( x, y) odgovara određenom stanju sistema.
Razmotrimo ravan s koordinatnim osa na kojoj su iscrtane vrijednosti varijabli x,y. Svaki poen M ova ravan odgovara određenom stanju sistema. Ova ravan se naziva fazna ravan i predstavlja ukupnost svih stanja sistema. Tačka M(x,y) naziva se reprezentativna ili reprezentativna tačka.
Neka u početnom trenutku vremena t=t 0 koordinate reprezentativne tačke M 0 (x(t 0), y(t 0)). U svakom narednom trenutku u vremenu t reprezentativna tačka će se pomeriti u skladu sa promenama vrednosti varijabli x(t), y(t). Prikupljanje bodova M(x(t), y(t)) na faznoj ravni, čiji položaj odgovara stanjima sistema u procesu promene varijabli tokom vremena x(t), y(t) prema jednadžbi (4.1), naziva se fazna putanja.
Skup faznih putanja za različite početne vrijednosti varijabli daje lako vidljiv „portret“ sistema. Izgradnja fazni portret omogućava vam da izvučete zaključke o prirodi promjena u varijablama x, y bez poznavanja analitičkih rješenja originalnog sistema jednačina(4.1).
Za prikaz faznog portreta potrebno je konstruisati vektorsko polje pravaca putanja sistema u svakoj tački fazne ravni. Podešavanje inkrementaD t>0,dobijamo odgovarajuće inkremente D x I D y iz izraza:
D x=P(x,y)D t,
D y=Q(x,y)D t.
Vektorski smjer dy/dx u tački ( x, y) zavisi od predznaka funkcija P(x, y), Q(x, y) i može se dati tabelom:
|
P(x,y)>0,Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
Rješenje ove jednačine y = y(x,c), ili implicitno F(x,y)=c, Gdje With– konstanta integracije, daje porodicu integralnih krivulja jednadžbe (4.2) - fazne trajektorije sistema (4.1) na ravni x, y.
Izoklina metoda
Za konstruiranje faznog portreta koriste se izoklina metoda - na faznoj ravni se crtaju linije koje sijeku integralne krive pod jednim određenim uglom. Jednačina izokline se može lako dobiti iz (4.2). Hajde da stavimo
Gdje A– određenu konstantnu vrijednost. Značenje A predstavlja tangentu ugla nagiba tangente na faznu putanju i može uzimati vrijednosti od –¥ do + ¥ . Umjesto toga dy/dx u (4.2) količinu A dobijamo jednačinu izoklina:
.(4.3)
Jednačina (4.3) definiše u svakoj tački ravni jedinstvenu tangentu na odgovarajuću integralnu krivu, sa izuzetkom tačke u kojoj P(x,y)= 0, Q (x,y) = 0 , u kojem smjer tangente postaje neizvjestan, budući da vrijednost derivacije postaje neizvjesna:
.
Ova tačka je tačka preseka svih izoklina - posebna tačka. U njemu, vremenski derivati varijabli istovremeno nestaju x I y.
Dakle, u singularnoj tački, stope promjene varijabli su nule. Prema tome, singularna tačka diferencijalnih jednadžbi faznih putanja (4.2) odgovara stacionarno stanje sistema(4.1), a njegove koordinate su stacionarne vrijednosti varijabli x, y.
Od posebnog interesa su glavne izokline:
dy/dx=0, P(x,y)=0 – izoklina horizontalnih tangenti i
dy/dx=¥ , Q(x,y)=0 – izoklina vertikalnih tangenti.
Konstruisanjem glavnih izoklina i pronalaženjem njihove tačke preseka (x,y), čije koordinate zadovoljavaju uslove:
time ćemo naći tačku preseka svih izoklina fazne ravni, u kojoj je nesiguran smer tangenti na fazne trajektorije. ovo - singularna tačka, što odgovara stacionarno stanje sistema(Sl. 4.2).
Sistem (4.1) ima onoliko stacionarnih stanja koliko ima tačaka preseka glavnih izoklina na faznoj ravni.
Svaka fazna putanja odgovara skupu kretanja dinamičkog sistema, koji prolaze kroz ista stanja i razlikuju se jedno od drugog samo u početku odbrojavanja vremena.
 |
|
Ako su ispunjeni uslovi Cauchyjeve teoreme, onda kroz svaku tačku u prostoru x, y, t postoji samo jedna integralna kriva. Isto važi, zbog autonomije, za fazne putanje: jedna fazna putanja prolazi kroz svaku tačku fazne ravni.
Stabilnost u stabilnom stanju
Neka je sistem u stanju ravnoteže.
Tada se reprezentativna tačka nalazi u jednoj od singularnih tačaka sistema, u kojoj je, po definiciji:
.
Da li je singularna tačka stabilna ili ne određuje se da li ta tačka koja predstavlja izlazi sa malim odstupanjem od stacionarnog stanja ili ne. U odnosu na sistem od dvije jednačine, definicija stabilnosti u jezikue, dizgleda ovako.
Stanje ravnoteže je stabilno ako za bilo koji dati raspon odstupanja od ravnotežnog stanja (e )možete odrediti područje d (e ), koji okružuje ravnotežno stanje i ima svojstvo da nema putanje koja počinje unutar regije d , nikada neće stići do granice e . (Sl. 4.4)
 |
|
Za veliku klasu sistema - grubi sistemi – priroda čijeg se ponašanja ne mijenja s malom promjenom oblika jednadžbi, informacija o tipu ponašanja u blizini stacionarnog stanja može se dobiti ispitivanjem ne originalnog, već pojednostavljenog linearizovano sistem.
Linearni sistemi.
Razmotrite sistem od dva linearne jednačine:
.(4.4)
Evo a, b, c, d- konstante, x, y- Kartezijanske koordinate na faznoj ravni.
Općenito rješenje ćemo tražiti u obliku:
.(4.5)
Zamijenimo ove izraze u (4.4) i smanjimo za e l t:
(4.6)
Algebarski sistem jednadžbi (4.6) sa nepoznanicama A, B ima rješenje različito od nule samo ako je njegova determinanta, sastavljena od koeficijenata za nepoznate, jednaka nuli:
.
Proširujući ovu determinantu, dobijamo karakterističnu jednačinu sistema:
.(4.7)
Rješavanje ove jednadžbe daje vrijednosti eksponental 1,2 , za koje su moguće vrijednosti različite od nule A I B rješenja jednačine (4.6). Ova značenja su
.(4.8)
Ako je radikalni izraz negativan, ondal 1,2 kompleksno konjugirani brojevi. Pretpostavimo da oba korijena jednadžbe (4.7) imaju realne dijelove različite od nule i da nema višestrukih korijena. Tada se opće rješenje sistema (4.4) može predstaviti kao linearna kombinacija eksponencijala sa eksponentimal 1 , l 2 :
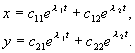(4.9)
Za analizu prirode mogućih putanja sistema na faznoj ravni koristimo se linearna homogena transformacija koordinata,što će dovesti sistem do kanonski oblik:
,(4.10)
omogućavajući pogodnije predstavljanje na faznoj ravni u poređenju sa originalnim sistemom (4.4). Hajde da uvedemo nove koordinateξ , η prema formulama:
(4.1)
Iz kursa linearne algebre poznato je da su u slučaju nejednakosti na nulu realni dijelovil 1 , l 2 originalni sistem (4.4) se uvek može transformisati pomoću transformacija (4.11) u kanonski oblik (4.10) i može se proučavati njegovo ponašanje na faznoj ravniξ , η . Hajde da razmotrimo različite slučajeve koji se ovde mogu pojaviti.
Korijeni λ 1 , λ 2 – važeći i istog znaka
U ovom slučaju koeficijenti transformacije su realni, krećemo se od realne ravnix,yna realnu ravan ξ, η. Dijelimo drugu od jednadžbi (4.10) prvom, dobijamo:
.(4.12)
Integracijom ove jednačine nalazimo:
Gdje .(4.13)
Složimo se da razumijemo pod λ 2 korijen karakteristične jednadžbe s velikim modulom, koji ne narušava općenitost našeg zaključivanja. Zatim, budući da su u predmetnom slučaju korijeni λ 1 , λ 2 – važeći i istog znaka,a>1 , a radi se o integralnim krivuljama paraboličkog tipa.
Sve integralne krive (osim ose η , što odgovara ) dodir na početku ose ξ, što je ujedno i integralna kriva jednačine (4.11). Porijeklo koordinata je posebna tačka.
Otkrijmo sada smjer kretanja reprezentativne točke duž faznih putanja. Ako je λ 1 , λ 2 negativni su, dakle, kao što se vidi iz jednačina (4.10), |ξ|, |η| vremenom smanjiti. Reprezentirajuća tačka se približava ishodištu koordinata, ali nikada do njega ne stiže. U suprotnom, ovo bi bilo u suprotnosti sa Cauchyjevom teoremom, koja kaže da samo jedna fazna putanja prolazi kroz svaku tačku fazne ravni.
Tako posebna tačka kroz koju prolaze integralne krive, baš kao porodica parabola 
prolazi kroz ishodište i naziva se čvor (sl. 4.5)
Stanje ravnoteže tipa čvora na λ 1 , λ 2 < 0 je Lyapunov stabilan, jer se reprezentativna tačka kreće duž svih integralnih krivih prema ishodištu koordinata. Ovo stabilan čvor. Ako je λ 1 , λ 2 > 0, onda |ξ|, |η| povećavaju se tokom vremena i predstavljana tačka se udaljava od početka koordinata. U ovom slučaju, posebna točka– nestabilan čvor .
Na faznoj ravni x, y opća kvalitativna priroda ponašanja integralnih krivulja će biti očuvana, ali se tangente na integralne krive neće poklapati sa koordinatnim osa. Ugao nagiba ovih tangenata će biti određen omjerom koeficijenata α , β , γ , δ u jednačinama (4.11).
Korijeni λ 1 , λ 2 – važeće su i različitih znakova.
Pretvori iz koordinate x,y na koordinate ξ, η opet pravi. Jednačine za kanonske varijable opet imaju oblik (4.10), ali sada predznaci λ 1 , λ 2 su različiti. Jednačina faznih putanja ima oblik:
Gdje ,(4.14)
Integrirajući (4.14) nalazimo
(4.15)
Ovo jednadžba definira familiju krivulja hiperboličkog tipa, gdje su obje koordinatne ose– asimptote (na a=1 imali bismo porodicu ekvilateralnih hiperbola). Koordinatne ose u ovom slučaju su također integralne krive– ovo će biti jedine integralne krive koje prolaze kroz ishodište. Svakiod kojih se sastoji od tri fazne trajektorije: dva kretanja u stanje ravnoteže (ili iz stanja ravnoteže) i iz stanja ravnoteže. Sve ostale integralne krive– su hiperbole koje ne prolaze kroz ishodište koordinata (Sl. 4.6) Ova posebna tačka se zove "sedlo ». Linije nivoa u blizini planinskog sedla ponašaju se slično kao i fazne putanje u blizini sedla.
Razmotrimo prirodu kretanja reprezentativne tačke duž faznih trajektorija u blizini ravnotežnog stanja. Neka, na primjer,λ 1 >0 , λ 2<0 . Zatim je reprezentativna tačka postavljena na osu ξ , će se udaljiti od početka i postaviti na osu η – će se neograničeno približavati početnu koordinata, a da ga ne stigne u konačnom vremenu. Gdje god je reprezentativna tačka u početnom trenutku (sa izuzetkom singularne tačke i tačaka na asimptoti η =0), na kraju će se udaljiti od ravnotežnog stanja, čak i ako se u početku kreće duž jedne od integralnih krivulja prema singularnoj tački.
Očigledno je da singularna tačka kao što je sedlo je uvek nestabilna . Samo pod posebno odabranim početnim uslovima na asimptotiη =0 sistem će se približiti stanju ravnoteže. Međutim, to nije u suprotnosti sa tvrdnjom o nestabilnosti sistema. Ako računamo, da su sva početna stanja sistema na faznoj ravni podjednako verovatna, onda je verovatnoća takvog početnog stanja koje odgovara kretanju u pravcu To singularna tačka je jednaka nuli. Stoga, svako stvarno kretanje će ukloniti sistem iz stanja ravnoteže.Vraćam se na koordinatex,y,dobićemo istu kvalitativnu sliku prirode kretanja trajektorija oko ishodišta koordinata.
Granica između razmatranih slučajeva čvora i sedla je slučaj Kada jedan od karakterističnih pokazatelja, na primjer λ 1 , nestaje, što se dešava kada je determinanta sistema– izražavanje ad-bc=0(vidi formulu 4.8 ). U ovom slučaju, koeficijenti desne strane jednačine (4.4) su proporcionalni jedni drugima:
a sistem ima kao stanje ravnoteže sve tačke prave:
Preostale integralne krive su porodica paralelnih pravih linija sa ugaonim koeficijentom , duž koje se reprezentativne tačke ili približavaju ravnotežnom stanju ili se udaljavaju od njega, ovisno o predznaku drugog korijena karakteristične jednadžbe λ 2 = a+d.(Sl.4. 7 ) U ovom slučaju koordinate ravnotežnog stanja zavise od početne vrijednosti varijabli.
Korijeni λ 1 , λ 2 – komplekskonjugirati
U ovom slučaju, stvarnox I y mi ćemo imaju kompleksne konjugate ξ , η (4.10) . Međutim, uvođenjem druge međutransformacije, moguće je i u ovom slučaju svesti razmatranje na realnu linearnu homogenu transformaciju. Hajde da stavimo:
(4.16)
Gdje a,b, I u,v – stvarne vrijednosti. Može se pokazati da transformacija izx,y To u,v je, prema našim pretpostavkama, realan, linearan, homogen sa determinantom različitom od nule. Na osnovu jednačina(4.10, 4.16) imamo:
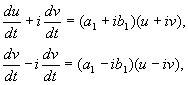
gdje
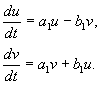(4.17)
Dijeljenje druge jednadžbe s prvom, dobijamo:
koje je lakše integrisati, ako idemo na polarni koordinatni sistem (r, φ ) . Nakon zamjene dobijamo odakle:
.(4.18)
Dakle, na faznoj ravniu, vimamo posla sa porodicom logaritamskih spirala, od kojih svaka imaasimptotska tačka na početku.Singularna tačka, koja je asimptotska tačka svih integralnih krivulja koje imaju oblik spirale, ugniježđene u svakojprijatelju, to se zove fokus ( Sl.4.8 ) .
Razmotrimo prirodu kretanja reprezentativne tačke duž faznih putanja. Množenje prve od jednačina (4.17) sau, a drugi na v i dodajući, dobijamo:
Gdje
Neka a 1 < 0 (a 1 = Reλ ) . Reprezentirajuća tačka se tada kontinuirano približava ishodištu koordinata, a da ne stigne do njega u konačnom vremenu. To znači da su fazne putanje spirale koje se uvijaju i odgovaraju prigušenim oscilacijama varijable. ovo - stabilan fokus .
U slučaju stabilnog fokusa, kao iu slučaju stabilnog čvora, nije zadovoljen samo uslov Ljapunova, već i stroži uslov. Naime, za sva početna odstupanja, sistem će se vremenom vratiti koliko god želi u ravnotežni položaj. Takva stabilnost, u kojoj početna odstupanja ne samo da se ne povećavaju, već opadaju, težeći nuli, naziva se apsolutna stabilnost .
Ako je u formuli (4.18) a 1 >0 , tada se reprezentativna tačka udaljava od početka, a mi imamo posla nestabilan fokus . Kada se krećete iz avionau,vna faznu ravanx, yspirale će takođe ostati spiralne, ali će biti deformisane.
Razmotrimo sada slučaj kadaa 1
=0
. Fazne putanje u ravniniu, vbiće krugovi 
koji u avionux,yodgovaraju elipsama:
Dakle, kadaa 1=0 kroz posebnu tačkux= 0, y= 0 nijedna integralna kriva ne prolazi. Takva izolovana singularna tačka, u blizini koje su integralne krive zatvorene krive, posebno elipse uklopljene jedna u drugu i koje okružuju singularnu tačku, naziva se centar.
Dakle, moguće je šest tipova ravnotežnih stanja, u zavisnosti od prirode korena karakteristične jednačine (4.7). Pogled na fazne trajektorije na ravni x, y za ovih šest slučajeva prikazano je na sl. 4.9.
Rice. 4.9.Vrste faznih portreta u blizini stacionarnog stanja za sistem linearnih jednačina (4.4).
Pet tipova ravnotežnih stanja su grubi, njihov karakter se ne menja sa dovoljno malim promenama u desnim stranama jednačine (4.4). U ovom slučaju, promjene ne samo na desnim stranama, već iu njihovim derivatima prvog reda trebaju biti male. Šesto stanje ravnoteže – centar – nije grubo. Uz male promjene parametara desne strane jednadžbe, postaje stabilan ili nestabilan fokus.
Bifurkacijski dijagram
Hajde da uvedemo sljedeću notaciju:
.
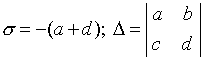(4.11)
Tada će se karakteristična jednačina napisati kao:
.
(4.12)
Zamislite ravan s pravokutnim dekartovskim koordinatama s , D i označite na njemu područja koja odgovaraju jednom ili drugom tipu stanja ravnoteže, koje je određeno prirodom korijena karakteristične jednadžbe
.(4.13)
Uslov za stabilnost ravnotežnog stanja biće prisustvo negativnog realnog dela yl 1 i l 2 . Neophodan i dovoljan uslov za to je ispunjenje nejednakostis > 0, D > 0 . U dijagramu (4.15), ovaj uslov odgovara tačkama koje se nalaze u prvoj četvrtini parametarske ravni. Jedinstvena tačka će biti fokus akol 1 i l 2 kompleks. Ovaj uslov odgovara onim tačkama ravni za koje , one. tačke između dve grane paraboles 2 = 4 D. Osovine s = 0, D>0, odgovaraju ravnotežnim stanjima tipa centra. Isto tako,l 1 i l 2 - važeće su, ali različitih predznaka, tj. singularna tačka će biti sedlo ako D<0, itd. Kao rezultat, dobićemo dijagram podjele parametarske ravni s, D, u oblasti koje odgovaraju različitim tipovima ravnotežnih stanja.
Rice. 4.10. Bifurkacijski dijagram
za sistem linearnih jednadžbi 4.4
Ako su koeficijenti linearnog sistema a, b, c, d ovise o određenom parametru, onda kada se ovaj parametar promijeni, vrijednosti će se također promijenitis , D . Prilikom prelaska granica, karakter faznog portreta se kvalitativno mijenja. Stoga se takve granice nazivaju granicama bifurkacije - na suprotnim stranama granice sistem ima dva topološki različita fazna portreta i, shodno tome, dva različita tipa ponašanja.
Dijagram pokazuje kako do takvih promjena može doći. Ako izuzmemo posebne slučajeve - ishodište koordinata - onda je lako vidjeti da se sedlo može transformirati u čvor, stabilan ili nestabilan pri prelasku preko ordinatne ose. Stabilan čvor može ići ili u sedlo ili u stabilan fokus, itd. Imajte na umu da prijelazi stabilan čvor - stabilan fokus i nestabilan čvor - nestabilan fokus nisu bifurkacije, jer se topologija faznog prostora ne mijenja. Više o topologiji faznog prostora i bifurkacijskim prijelazima ćemo govoriti u 6. predavanju.
Tokom bifurkacionih prelaza, priroda stabilnosti singularne tačke se menja. Na primjer, stabilan fokus kroz centar može se pretvoriti u nestabilan fokus. Ova bifurkacija se zove Andronov-Hopf bifurkacija po imenima naučnika koji su ga proučavali. Tokom ove bifurkacije u nelinearnim sistemima, rađa se granični ciklus i sistem postaje samooscilirajući (vidi predavanje 8).
Primjer. Linearni sistem hemijskih reakcija
Supstanca X teče izvana konstantnom brzinom, pretvara se u tvar Y i brzinom proporcionalnom koncentraciji tvari Y, uklanja se iz sfere reakcije. Sve reakcije su prvog reda, sa izuzetkom priliva supstance izvana, koji je nultog reda. Shema reakcije izgleda ovako:
(4.14)
a opisuje se sistemom jednačina:
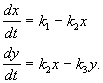(4.15)
Dobivamo stacionarne koncentracije izjednačavanjem desne strane sa nulom:
.(4.16)
Razmotrimo fazni portret sistema. Podijelimo drugu jednačinu sistema (4.16) prvom. dobijamo:
.(4.17)
Jednačina (4.17) određuje ponašanje varijabli na faznoj ravni. Hajde da napravimo fazni portret ovog sistema. Prvo, nacrtajmo glavne izokline na faznoj ravni. Jednadžba izokline vertikalnih tangenti:
Jednadžba izokline horizontalnih tangenti:
Singularna tačka (stacionarno stanje) leži na preseku glavnih izoklina.
Sada odredimo pod kojim uglom se koordinatne ose sijeku sa integralnim krivuljama.
Ako x= 0, zatim .
Dakle, tangenta tangente na integralne krive y=y(x), siječe os ordinate x=0, je negativan u gornjoj poluravni (zapamtite da su varijable x, y imaju vrijednosti koncentracije, pa nas stoga zanima samo gornji desni kvadrant fazne ravni). U ovom slučaju, tangenta kuta tangente raste s rastojanjem od početka.
Uzmite u obzir osu y= 0. U tački gdje ova osa siječe integralne krive, one su opisane jednadžbom
At tangenta nagiba integralnih krivulja koje prelaze osu apscise je pozitivna i raste od nule do beskonačnosti sa povećanjem x.
U .
Zatim, s daljim povećanjem, tangent ugla nagiba opada u apsolutnoj vrijednosti, ostaje negativan i teži -1 na x ® ¥ . Poznavajući smjer tangenti na integralne krivulje na glavnim izoklinama i na koordinatnim osa, lako je konstruirati cjelokupnu sliku faznih putanja.
 |
|
Utvrdimo prirodu stabilnosti singularne tačke pomoću metode Ljapunova. Karakteristična determinanta sistema ima oblik:
.
Proširujući determinantu, dobijamo karakterističnu jednačinu sistema: , tj. Korijeni karakteristične jednadžbe su negativni. Prema tome, stacionarno stanje sistema je stabilan čvor. U ovom slučaju, koncentracija tvari X teži stacionarnom stanju uvijek monotono, koncentracija supstance Y može proći kroz min ili max. Oscilatorni modovi su nemogući u takvom sistemu.
Singularna tačka u matematici. 1) Singularna tačka krive definisane jednadžbom F ( x, y) = 0, - tačka M 0 ( x 0 , y 0), u kojem oba parcijalna izvoda funkcije F ( x, y) idi na nulu: Ako nisu svi drugi parcijalni izvodi funkcije F ( x, y) u tački M 0 jednaki su nuli, tada se O. t naziva dvostrukim. Ako, zajedno sa prvim izvodima koji nestaju u tački M0, nestanu i svi drugi izvodnici, ali ne i svi treći izvod, tada se jednačina naziva trostruka, itd. Prilikom proučavanja strukture krive u blizini dvostrukog O.t., znak izraza igra važnu ulogu Ako je Δ > 0, tada se otvoreni prostor naziva izolovanim; na primjer, na krivulji y 2 - x 4 + 4x 2= 0 ishodište koordinata je izolovani O. t. pirinač. 1
). Ako je Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 ishodište koordinata je čvor O. t (vidi. pirinač. 2
). Ako je Δ = 0, onda je opća tačka krive ili izolovana ili je karakterizirana činjenicom da različite grane krive imaju zajedničku tangentu u ovoj tački, na primjer: a) vršna tačka 1. vrste - različite grane krive krive se nalaze na suprotnim stranama zajedničke tangente i formiraju tačku, poput krivulje y 2 - x 3= 0 (vidi pirinač. 3
, a); b) vršna tačka 2. vrste - različite grane krive se nalaze na jednoj strani zajedničke tangente, kao kriva
(y - x 2)2 - x 5= 0 (vidi pirinač. 3
, b); c) tačka samododira (za krivinu y 2 - x 4= 0 ishodište je tačka samododira; (cm. pirinač. 3
, V). Zajedno sa navedenim O. t. ima mnogo drugih O. t. na primjer, asimptotička tačka je vrh spirale s beskonačnim brojem zavoja (vidi. pirinač. 4
), tačka završetka, tačka ugla, itd. 2) Singularna tačka diferencijalne jednadžbe je tačka u kojoj i brojnik i imenilac desne strane diferencijalne jednadžbe istovremeno nestaju (vidi Diferencijalne jednadžbe) gdje su P i Q kontinuirano diferencibilne funkcije. Uz pretpostavku da se O. t nalazi na početku koordinata i koristeći Taylorovu formulu (vidi Taylorovu formulu), možemo predstaviti jednačinu (1) u obliku. gdje je P 1 ( x, y) i Q 1 ( x, y) - beskonačno malo u odnosu na Naime, ako je λ 1 ≠ λ 2 i λ 1 λ 2 > 0 ili λ 1 = λ 2, onda je O. t čvor; u njega ulaze sve integralne krive koje prolaze kroz tačke u dovoljno maloj okolini čvora. Ako je λ 1 ≠ λ 2 i λ 1 λ 2 i β, α ≠ 0 i β ≠ 0, onda je opšta tačka fokus; sve integralne krive koje prolaze kroz tačke u dovoljno maloj okolini fokusa predstavljaju spirale sa beskonačnim brojem zavoja u bilo kojoj proizvoljno maloj okolini fokusa. Ako je, konačno, λ 1,2 = ± iβ, β ≠ 0, onda karakter O. t nije određen samo linearnim članovima u proširenjima P (. x, y) i Q ( x, y), kao što je bio slučaj u svim gore navedenim slučajevima; ovdje O. t može biti fokus ili centar, ili može imati više složen karakter. U blizini centra sve integralne krive su zatvorene i sadrže centar u sebi. Tako, na primjer, tačka (0, 0) je čvor za jednačine at" = 2u/x(λ 1 = 1, λ 2 = 2; vidi pirinač. 5
, a) i y" = u/x(λ 1 = λ 2 = 1; vidi pirinač. 5
, b), sedlo za jednadžbu y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. pirinač. 6
), fokus za jednadžbu y" =(x + y) /
(x - y) (λ 1 = 1 - i, λ 2 = 1 + i; cm. pirinač. 7
) i centar za jednadžbu y" = -x/y(λ 1 = -i, λ 2 = i; cm. pirinač. 8
). Ako su x, y) i Q ( x, y) analitičko, susjedstvo O. t. višeg reda mogu se podijeliti na regije: D 1 - ispunjena integralnim krivuljama, oba kraja uključena u O. t (eliptičke regije), D 2 - ispunjena integralnim krivuljama, jedan kraj uključena u O. t (paraboličke regije). i D 3 - regije , ograničene sa dvije integralne krive uključene u opću teoriju, između kojih se nalaze integralne krive tipa hiperbole (hiperboličke regije) (vidi pirinač. 9
). Ako ne postoje integralne krive uključene u opštu tačku, onda se opšta tačka naziva tačka stabilnog tipa. Susjedstvo stabilnog oscilatora sastoji se od zatvorenih integralnih krivulja koje sadrže osmozu u sebi, između kojih se nalaze spirale (vidi Sl. pirinač. 10
). Proučavanje diferencijalnih jednadžbi, odnosno u suštini proučavanje ponašanja porodica integralnih krivulja u susjedstvu diferencijalnih jednadžbi, predstavlja jednu od grana kvalitativne teorije diferencijalnih jednadžbi i igra važnu ulogu u primjenama, posebno u pitanjima stabilnosti kretanja (rad A. M. Ljapunova, A. Poincarea, itd.). 3) Singularna tačka jednoznačne analitičke funkcije je tačka u kojoj je narušena analitičnost funkcije (vidi Analitičke funkcije). Ako postoji susjedstvo O. t. a, oslobođen od drugih O. t., a zatim pokažite A nazvan izolovani O. t A- izolovana opšta teorija i postoji konačno a naziva se uklonjivom opštom teorijom Prikladnom promenom definicije funkcije u tački a (ili njenim redefinisanjem u ovoj tački, ako funkcija u njoj uopšte nije definisana). naime, pretpostavkom f(a)= b, to je moguće postići a postat će obična tačka korigirane funkcije. Na primjer, tačka z= 0 je uklonjivi O. t za funkciju f 1 (. z) = f(z), Ako z≠ 0, i f 1 (0), = 1, tačka z= 0 je obična tačka [ f 1 (z) je analitičan u tački z= 0]. Ako A- izolovani O. t i a se nazivaju pol ili nebitno singularna tačka funkcije f(z), ako Laurentov niz) funkcionira f(z) u blizini izolovanog O. t ne sadrži negativne moći z - a, Ako A- uklonjivi O. t., sadrži konačan broj negativnih stupnjeva z - a, Ako A- motka (u ovom slučaju redoslijed motke r definisano kao najviši stepen a je suštinski singularna tačka. Na primjer, za funkciju dot z= 0 je pol reda r, za funkciju dot z= 0 je suštinski singularna tačka. Na granici kruga konvergencije potencijskog niza mora postojati barem jedan O.t funkcije predstavljene podacima power series. Sve granične tačke domena postojanja jedinstvene analitičke funkcije (prirodna granica) su granice ove funkcije. Dakle, sve tačke jedinične kružnice | z| = 1 su posebni za funkciju Za viševrijednu analitičku funkciju, koncept „O. T." teže. Pored O. t., u pojedinačnim listovima Rimanove površine funkcije (tj. O. t. jednoznačnih analitičkih elemenata), svaka tačka grananja je i O. t. Izolirane tačke grananja Riemannove površine (tj. takve tačke grananja da u nekom njihovom susjedstvu nema drugih O. t. funkcija ni u jednom listu) klasificiraju se na sljedeći način. Ako je a izolovana tačka grananja konačnog reda i postoji konačno a, naziva se kritični pol. Ako A- izolovana tačka grananja beskonačnog reda i a naziva se transcendentalna O.t. Sve ostale izolovane tačke grananja se nazivaju kritične suštinski singularne tačke. Primjeri: tačka z= 0 je obična kritična tačka funkcije f ( z) = log z i kritična suštinski singularna tačka funkcije f (z) = sin ln z. Svaka opća teorija, osim one koja se može ukloniti, prepreka je analitičkom nastavku, odnosno nemoguć je analitički nastavak duž krive koja prolazi kroz nesvodljivi opći problem. Veliki Sovjetska enciklopedija. - M.: Sovjetska enciklopedija.
1969-1978
.
p = 2, 3, …)
Pogledajte šta je "singularna tačka" u drugim rječnicima:
Poeni ovdje. Vidi također singularnu tačku ( diferencijalne jednadžbe). Karakteristika ili singularnost u matematici je tačka u kojoj je matematički objekt (obično funkcija) nedefiniran ili ima nepravilno ponašanje (na primjer, tačka u kojoj ... ... Wikipedia
Analitička funkcija je tačka u kojoj se krše uslovi analitičnosti. Ako je analitička funkcija f(z) data u određenom okruženju tačke z0 svuda... Fizička enciklopedija
Analitička funkcija je tačka u kojoj je narušena analitičnost funkcije... Veliki enciklopedijski rječnik
singularna tačka- - [Ya.N.Luginsky, M.S.Fezi Zhilinskaya, Yu.S.Kabirov. Englesko-ruski rečnik elektrotehnike i energetike, Moskva, 1999.] Teme elektrotehnike, osnovni pojmovi EN jednina ... Vodič za tehnički prevodilac
1) Analitička funkcija f(z) je prepreka analitičkom nastavku elementa funkcije f(z) kompleksne varijable z duž neke putanje u ravni ove varijable. Neka je analitička funkcija f(z) definirana nekim... ... Mathematical Encyclopedia
Analitička funkcija, tačka u kojoj je narušena analitičnost funkcije. * * * JEDNA TAČKA JEDNA TAČKA analitičke funkcije, tačka u kojoj je narušena analitičnost funkcije... Encyclopedic Dictionary
singularna tačka- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. singularna tačka vok. singulärer Punkt, m rus. singularna tačka, f pranc. tačka particulier, m; točka singulier, m … Automatikos terminų žodynas
singularna tačka- ypatingasis taškas statusas T sritis fizika atitikmenys: engl. singularna tačka vok. singulärer Punkt, m rus. singularna tačka, f pranc. točka singulier, m … Fizikos terminų žodynas
Osnovni koncepti i definicije:
Nula analitičke funkcije f(z) je tačka “a” za koju je f(a)=0.
Nula reda “n” funkcije f(z) je tačka “a” ako je fn(a)¹0.
Singularna tačka “a” naziva se izolovana singularna tačka funkcije f(z) ako postoji okolina ove tačke u kojoj nema singularnih tačaka osim “a”.
Postoje tri vrste izolovanih singularnih tačaka: .
1 uklonjive singularne tačke;
3 suštinski singularne tačke.
Tip singularne tačke može se odrediti na osnovu ponašanja date funkcije u pronađenoj singularnoj tački, kao i na osnovu oblika Lorentovog reda dobijenog za funkciju u okolini pronađene singularne tačke.
Određivanje tipa singularne tačke ponašanjem funkcije u njoj.
1. Uklonjive singularne tačke.
Izolovana singularna tačka a funkcije f(z) naziva se uklonjivom ako postoji konačan limit.
2.Poljaci.
Izolovana singularna tačka a funkcije f(z) naziva se pol if 
.
3. U suštini singularne tačke.
Izolovana singularna tačka a funkcije f(z) naziva se suštinski singularnom tačkom ako ne postoji ni konačna ni beskonačna.
Između nula i polova funkcije postoji sljedeća veza.
Da bi tačka a bila pol reda n funkcije f(Z), potrebno je i dovoljno da ta tačka bude nula reda n za funkciju .
Ako je n=1, pol se naziva jednostavnim.
definicija: Izolovana singularna tačka nedvosmislene prirode naziva se:
a) može se ukloniti ako nedostaje glavni dio raspadanja;
b) pol, ako glavni dio sadrži konačan broj članova;
c) suštinski singularna tačka ako glavni dio sadrži beskonačan broj pojmova.
a) Dakle, u okolini uklonjive singularne tačke, proširenje ima oblik:
izražava funkciju u svim tačkama kružnice |z-a| U centru z=a jednakost nije tačna, jer funkcija na z=a ima diskontinuitet, a desna strana je kontinuirana. Ako se vrijednost funkcije u centru promijeni, uzimajući je jednakom vrijednosti sa desne strane, tada će se praznina eliminirati - otuda i naziv - uklonjiv. b) U blizini pola reda m, proširenje Laurentovog reda ima oblik: c) U blizini obične motke Odbici i formule za njihovo izračunavanje. Ostatak analitičke funkcije f(z) u izolovanoj singularnoj tački z 0 je kompleksan broj jednak vrijednosti integrala Ostatak funkcije f(z) u izolovanoj singularnoj tački z 0 označava se simbolom Res f(z 0) ili Res (f(z); z 0). dakle, Res f(z 0)= Ako stavimo n=-1 u formulu (22.15.1), dobićemo: C -1 = ili Res f(z 0)= C -1 , one. ostatak funkcije f(z) u odnosu na singularnu tačku z 0 jednak je koeficijentu prvog člana sa negativnim eksponentom u proširenju funkcije f(z) u Lorentov red. Obračun odbitaka. Redovne ili uklonjive singularne tačke. Očigledno, ako je z=z 0 regularna ili uklonjiva singularna tačka funkcije f(z), tada je Res f(z 0)=0 (Laurentovom proširenju u ovim slučajevima nedostaje glavni dio, pa c-1=0) . Pole. Neka je tačka z 0 prost pol funkcije f(z). Tada Laurentov red za funkciju f(z) u blizini tačke z 0 ima oblik: Odavde Stoga, prelazeći ovu jednakost do granice na z --z 0, dobijamo Res f(z0)= U suštini posebna tačka. Ako je tačka z 0 suštinski singularna tačka funkcije f(z), tada se za izračunavanje ostatka funkcije u ovoj tački obično direktno određuje koeficijent c-1 u proširenju funkcije u Lorentov red. Klasifikacija događaja. Zbir, proizvod događaja, njihova svojstva, grafički prikaz. Događaji su podijeljeni na: 1. Slučajno 2. Pouzdan 3. Nemoguće Pouzdan je događaj koji se nužno dešava u datim uslovima (noć slijedi jutro). Slučajni događaj je događaj koji se može dogoditi ili ne mora (polaganje ispita). Nemogući događaj je događaj koji se neće dogoditi pod datim uslovima (vađenje zelene olovke iz kutije sa samo crvenim). Neka zq je singularna tačka funkcije /(r), t.s. f(z) ali je u ovom trenutku analitičan (posebno, možda nije definiran u njemu). Ako postoji tako probijeno susjedstvo tačke zq (tj. skup O z - zq f(z) je onda aialitic zo pozvao izolovana singularna tačka funkcije f(z). Ova definicija ostaje ista u slučaju zn = oo, ako je jod probušen u blizini tačke zq = oo razumjeti skup z> I -
spoljašnjost kružnice sa središtem u početku. Drugim riječima, posebna tačka zq se kaže da je izolovan ako postoji susjedstvo ove tačke u kojoj je ist drugih singularnih tačaka osim zq. U nastavku razmatramo samo singularne tačke jedinstvenog karaktera (funkcija f(z) pretpostavlja se da je nedvosmislen). Ovisno o ponašanju funkcije f(z) at z -> zq Postoje tri vrste singularnih tačaka. Izolovana singularna tačka zq funkcije f(z) zove: 1) uklonjiva singularna tačka, ako postoji konačan limit 2) pole, ako postoji granica 3) u suštini posebna tačka, Ako f(z) nema ni konačnu ni beskonačnu granicu na z-> zq. Primjer 26.1. Pokažimo da su sve tri vrste singularnih tačaka realizovane. Hajde da razmotrimo f(z)= Tačka zq = 0 je izolirano posebna tačka ove funkcije. Koristeći formulu (22.12), dobijamo ekspanziju iz čega proizlazi da postoji lim fi(z)= 1. Stoga je zq = 0 je uklonjiva singularna tačka funkcije fi(z). Funkcija f‘j(z) =---ima štap u tački zo= 1 jer 2
r“ X Razmotrimo sada funkciju )z(z)= e 1 ^ r i pokaži to zo = O je suštinski singularna tačka ove funkcije. Kada težite z na nulu duž realne ose lijevu i desnu granicu funkcije /z (z) različito: lim With 1 / 1
=
0, lim s 1 /* = os. Iz ovoga proizilazi, x->0-0 x->0+O sta f:i(z) nema ni konačnu ni beskonačnu granicu na 2 ->
Oh, to je. zq = O je suštinski singularna tačka ove funkcije. (Imajte na umu da kako poenta teži z - iy na nulu duž funkcije imaginarne ose nema ograničenja.) Postoje, naravno, neizolovane singularne tačke. Na primjer. funkcija ima polove u tačkama z n = -, n= ±1, ±2,... dakle, Zq = 0 je neizolovana singularna tačka ove funkcije: u bilo kojoj (bez obzira koliko mala) okolina ove tačke postoje druge singularne tačke g str.
Neka zo- konačna izolovana singularna tačka funkcije f(z). Onda f(z) je sličan u nekom probušenom susjedstvu 0 Zo tačke zo ovo susjedstvo se može smatrati prstenom unutrašnjeg polumjera r = 0. Prema teoremi 25.1, u susjedstvu koja se razmatra funkcija f(z) može se proširiti u Lorentov niz (25.2). Pokazat ćemo da je ponašanje funkcije na 2 -> zq (tj. tip singularne tačke zo) zavisi od vrste glavnog dela proširenja (25.2); Ova okolnost objašnjava porijeklo pojma „glavni dio“. Teorema 2G.2. Izolovana singularna točka zo funkcije f(z) je uklonjiva ako i samo ako Lorapova ekspanzija u probijenoj okolini ove tačke ima oid one. sastoji se samo od ispravnog dijela, a svi koeficijenti glavnog dijela jednaki su metku. Dokaz. 1. Neka zo- singularna tačka koja se može ukloniti. Dokažimo da je Laurentova ekspanzija funkcije f(z) ima oblik (26.1). Od posebne tačke zo uklonjiv, tada postoji konačna granica lim f(z) = A. dakle, f(z) je ograničen u nekom probušenom susjedstvu tačke 0 z - zq zo, one. )(z) za sve z iz ove blizine. Uzmimo bilo koje r. U r /?| i koristite formule (25.3) za koeficijente Laurentovog reda: Za koeficijente glavnog dijela ekspanzije n =- 1,-2,... Za takve vrednosti n imamo p~ str-e 0 at r-> 0. Od vrijednosti r onda se može izabrati koliko god želite Mr~" može biti mali po želji. Pošto |s t,| ^ Mr~p i c„ ne zavise od p, tada je c„ = 0 at I= - 1, -2,..., što je trebalo dokazati. 2. Pretpostavimo sada da Lorentova ekspanzija ima oblik (26.1). Niz (26.1) je stepen potencijskog niza i. stoga se konvergira ne samo u probijenom području, već iu cijeloj blizini z-zq uključujući poentu zo; njen iznos S(z) je analitičan u z i S(z) = )(z) na 0 z - zo R. Stoga postoji konačan limit lim )(z)= Pt 5(g) = 5(th) - Dakle, singularna tačka zq Z->Zo Z-*Zo uklonjiv. Teorema je dokazana. Komentar. Iz dokaza teoreme slijedi da je u probušenoj okolini 0 z - zo uklonjive singularne tačke funkcija f(z) poklapa se sa funkcijom 5(r), koja je analitička u cijelom susjedstvu z - zo. Stoga, ako postavimo /(th) = S(zq), zatim, bez promjene vrijednosti funkcije f(z) u bilo kojoj tački probijenog susjedstva, ovu funkciju ćemo učiniti analitičkom u Go, tj. Hajde da "eliminišemo" funkciju. Ovo objašnjava pojam „uklonjive karakteristike“. Prirodno je smatrati da su takve tačke regularne, a ne singularne tačke funkcije f(z).
Razmotrimo, na primjer, funkciju U primjeru 26.1 pokazano je da je Pm Nr) = 1. tj. singularna tačka zq = 0 uklonjivo. Postavljanjem /i(0) = 1, time eliminišemo singularnost i dobijamo funkciju koja je analitična u tački zq = 0 (i u cijeloj C ravni). Hajdemo sada da okarakterišemo polove u terminima Laurentovih ekspanzija. Teorema 26.3. Izolovana singularna tačka Zo funkcije f(z) je pol ako i samo ako, kada glavni dio Lorentove ekspanzije sa centrom Zq ima samo konačan broj različitih od nula koeficijenata sa n: Dokaz. 1. Neka zq - stub, tj. lim/( z) = oo. Dokažimo da je Laurentova ekspanzija funkcije f(z) ima oblik (2G.2). Od lim f(z)= oo. onda postoji probušena okolina tačke ki zq. u kojoj f(z) je analitičan i nema nule. Zatim funkcija g(z) = 1 /f(z)će također biti analitički u ovom probijenom susjedstvu, a lim g(z)= 0. Prema tome, Zo je uklonjiv *-? *0 singularna tačka funkcije g(z). Hajde da definišemo g(z) u tački zo, stavljanje g(zo)=
0. Onda g(z)će postati analitičan u cijelom susjedstvu (ne probijene) tačke z 0 , i z 0će biti njena izolovana nula. Označimo sa N višestrukost (red) ove nule. Kao što je pokazano u §23, u blizini tačke zq funkcija g(z) može se predstaviti u obliku (vidi (23.2)) i (z$) f 0 i y>(z) je analitičan u nekom susjedstvu tačke zo- Jer ip(z) kontinuirano u jednoj tački zo I g>(zo) F 0" tada ip(z) nema nule u nekom susjedstvu ove tačke. Stoga funkcija 1 /-p(z)će također biti analitičan u ovom susjedstvu i stoga se u njemu proširuje u Taylorov niz: Otvarajući zagrade i mijenjajući oznake koeficijenata, upisujemo posljednju ekspanziju u obliku gdje je c_jv = 1>o f 0. Dakle, glavni dio Laurentove ekspanzije funkcije /(r) sadrži samo konačan broj članova; došli smo do željene jednakosti (26.2). 2. Pustiti u probijenom susjedstvu tačaka th funkcija )(z) predstavljen je Laurentovom ekspanzijom (26.2) (za detaljniji oblik vidi (26.3)), čiji glavni dio sadrži samo konačan broj pojmova, i sa- d" f 0. To je potrebno dokazati Zq - funkcijski stup f(z). Množenje jednakosti (26.3) sa (G - G o) iV , dobijamo funkciju Niz u (26.4) je niz stepena koji konvergira analitičkoj funkciji ne samo u probušenoj tački, već iu cijeloj okolini tačke Zq. Stoga funkcija h(z) postat će analitičan u ovom susjedstvu ako ga dalje definiramo u go stavljanjem h(zo)= s_dg f 0. Onda Dakle, tačka th je pol, a teorema 26.3 je dokazana. Višestrukost (red) nulte funkcije g(z)= 1//(g) se poziva pole order ta funkcija /(r). Ako N- redom pola th, onda g(z)= (g - Zo) N ip(z), i (idi) F 0, i, kao što je prikazano u prvom dijelu dokaza teoreme 26.3, proširenje funkcije /(r) ima oblik (26.3), gdje je c_/v f 0. Obrnuto, ako se /(r) proširi u niz (26.3) i e-i F 0, onda t.s. N- red pola funkcije /(r). dakle, red polova funkcije zq/(G) jednak je broju najvećeg koeficijenta različitog od nule glavnog dijela Laurentove ekspanzije u probijenoj okolini tačke zq(tj. jednako ovom broju N,šta s_dg f 0 i Sp= 0 at n > N). Dokažimo sljedeću tvrdnju koja je pogodna za aplikacije. Korolar 26.4. Tačka zq je pol reda N fikcije/(G) tada i samo kada/(G) predstaviti u obliku gdje je h(z) analitička funkcija u blizini tačke th i h(zo) f 0. Dokaz. Funkcija cp(z) = l/h(z) je analitičan u nekoj okolini tačke h. Uslov zasljedice 26.4 je ekvivalentan sljedećem: Zato zq -
nulta množina N funkcije g(z). a samim tim i pol višestrukosti N funkcije /(2). II Primjer 26.5. Pronađite izolirane singularne točke funkcije Rješenje: Tačke u kojima (z 2
+ 1 )(z+ Z) 2 = 0. Ako z 2
L- 1 = 0, zatim 2 = ±g Ako (z 4- 3) 2 = 0, onda z= -3. Stoga funkcija ima tri singularne točke z= g, 22 = -g, Z3
=
- 3. Razmislite z: G - pol prvog reda (koristili smo korolar 26.4). Na sličan način se može dokazati da je 22 = -i takođe stub prvog reda. Za 2z imamo: Idemo dalje na razmatranje suštinski singularnih tačaka. Teorema 26.6. Izolovana singularna tačka zq funkcije f(z) je suštinski singularna ako i samo ako glavni dio Laurentove ekspanzije sa centrom zq ima beskonačno mnogo različitih od. nula, koeficijenti iz str. Dokaz. Teorema 26.6 direktno slijedi iz teorema 26.2 i 26.3. Zaista, ako je poenta zq je u suštini poseban, tada glavni dio Laurentove ekspanzije ne može izostati niti sadržavati konačan broj članova (inače tačka Zq će biti ili uklonjiv ili stup). Dakle, broj članova u glavnom dijelu mora biti beskonačan. Obrnuto, ako glavni dio sadrži beskonačno mnogo pojmova, onda Zq ne može biti ni uklonjiva tačka ni stub. Iz toga slijedi da je ova tačka suštinski posebna. Prema definiciji, suštinski singularnu tačku karakteriše činjenica da funkcija /(2) nema ni konačnu ni beskonačnu granicu za z ->zq. Potpuniju ideju o tome koliko je ponašanje funkcije nepravilno u blizini suštinski singularne tačke daje sljedeća teorema. Teorema 26.7 (teorema Sohotskog). Ako je zq bitno za osobe, tačka funkcije f(z), zatim za bilo koji kompleksni broj L, uključujući A = oh, postoji niz tačaka z n takav da je z n -> zo i lim f(zn) = A. p->os Dokaz. Hajde da prvo razmotrimo slučaj A = oo. U prvom dijelu dokaza teoreme 2G.2 utvrdili smo da ako f(z) je ograničen u nekom probušenom okruženju tačke r, tada su svi koeficijenti c", n = - 1,- 2,... glavnog dijela jednaki su nuli (i stoga je singularnost u go uklonjiva). Pošto je po uslovu th bitna singularna tačka, onda je u bilo kojoj probušenoj okolini tačke th funkcija f(r) neograničena. Uzmimo neku jaku okolinu 0 Z tako da f(zi) > 1 (ako |/(r)| z - zo I/2 postoji tačka z-2
, u kojem |/(yy)| > 2 itd.: u probijenom naselju O 71.
Očigledno je da je r„ -e go i lim /(r“) = oo. Dakle, u slučaju A = oo, teorema 26.7 dokazano. Pusti to sada A f oo. Pretpostavimo prvo da postoji probijeno susjedstvo 0 = -yy----
će biti analitičan u ovom probušenom kvartu i, posljedično, /(G) - A Prema tome, go je izolovana singularna tačka funkcije Φ(r). pokazaćemo ti. da je r suštinski singularna tačka Φ(r). Ovo možda nije istina. Tada postoji limit lim F(r), konačan ili beskonačan. Neko vrijeme /(r) = A + , tada postoji i Hsh /(r), što je u suprotnosti sa uslovom F(g) ~ :-*z 0 Vidim teoremu. Dakle, r0 je suštinski singularna tačka funkcije Φ(r). Prema onome što je gore dokazano, postoji niz tačaka r n takav da je r n th i lim F(r n) = oo. Odavde Dokazali smo traženu tvrdnju pod pretpostavkom da je /(r) F A u nekom probušenom okruženju tačke go- Pretpostavimo sada da je ovo netačno, tj. u bilo kojoj proizvoljno maloj probušenoj okolini tačke th postoji takva tačka G", da je /(r") = L. Tada za bilo koje n u probijenoj okolini 0 f(z u) = A Dakle, željena tvrdnja je tačna n-yuo u svim slučajevima, te je teorema 26.7 dokazana. Prema teoremi 26.7 (Sokhotsky), u bilo kojoj (proizvoljno maloj) probušenoj četvrti suštinski singularne tačke, funkcija /(r) uzima vrijednosti proizvoljno bliske bilo kojem broju iz proširene kompleksne ravni C. Za proučavanje izolovanih singularnih tačaka često su korisne već poznate Taylorove ekspanzije osnovnih elementarnih funkcija. Primjer 2G.8. Odrediti tip singularne tačke zq = 0 za funkciju Rešeno i e Proširimo brojilac i nazivnik u Tejlorov red po stepenu g z umjesto r i oduzimanja 1, dobijamo Koristeći (22.12), dobijamo proširenje nazivnika: Nizovi u ovim ekspanzijama konvergiraju u čitavoj kompleksnoj ravni €. Imamo i /2(2) su anaritični u susjedstvu tačke zo = 0 (pa čak i u cijeloj ravni) i /2(20) F 0, onda h(z) je također analitičan u nekoj okolini tačke gF 0. Prema korolaru 26.4, tačka Zo = 0 je pol reda N=4. II Primjer 26.9. Pronađite singularne tačke funkcije f(z)= sin j - i odredimo njihov tip. R e in e i e Funkcija ima jednu konačnu singularnu točku zq = 1. U ostalim tačkama iz C funkcija w =--- analitički; dakle funkcija sin w biće analitički. Zamjena - umjesto r u ekspanziju sinusa (22.12), dobijamo Dobili smo ekspanziju funkcije sin u Lorentov red u probijenoj okolini tačke 2o = 1. Pošto rezultirajuća ekspanzija sadrži beskonačno mnogo članova negativnih snaga (r - 1), onda zq = 1 je suštinski singularna tačka (u ovom slučaju, Lorentova ekspanzija se sastoji samo od glavnog dela, a regularni deo nedostaje). Imajte na umu da je u ovom slučaju bilo moguće utvrditi prirodu singularnosti direktno iz definicije, bez pribjegavanja proširenju serije. Zaista, postoje nizovi (r") i (2") koji konvergiraju zo= 1, i tako da f(z"n)= 1, /(2") = 0 (navedite takve nizove sami). Dakle, f(z) nema ograničenja na z -> 1 i stoga tačka zq - 1 je u suštini poseban. Hajde da uvedemo koncept Lorentove ekspanzije funkcije u okolini tačke Zq = 00 i razmotrimo vezu između ekspanzije i prirode singularnosti u ovoj tački. Imajte na umu da se definicije izolirane singularne točke i njenog tipa (uklonjive, polne ili suštinski singularne) prenose na slučaj zq = oc bez promjena. Ali teoreme 26.2. 26.3 i 26.6, koji se odnose na prirodu Laurentovih proširenja, treba promijeniti. Poenta je da članovi cn(z- 2o) str. n= -1,-2,..., glavni dio, definiranje “nepravilnosti” funkcije blizu krajnje točke Zq, kako 2 teži oo, ponašat će se "ispravno" (težu ka 0). Naprotiv, članovi pravilnog dijela s n= 1,2,... težiće ka oo; oni određuju prirodu karakteristike u Zq = oo. Stoga će glavni dio ekspanzije u blizini oo činiti termini sa pozitivnim moćima p, a ispravan - sa negativnim. Hajde da uvedemo novu varijablu w = 1/2. Funkcija tv = 1/2, proširen tako da je u(oo) = 0, jedan prema jedan i konformno preslikava susjedstvo z > R bodova zq = 00 u blizini |w| wq = 0. Ako je funkcija f(z) analitika u probijenom kraju R z Zq = oc, tada funkcija G(w) = f(l/w)će biti analitičan u velikoj okolini 0 wo = 0. Pošto će na 2 -> oo biti w-> 0, onda Zato G(w) ima u tački wq = 0 je karakteristika istog tipa kao f(z) u tački Zq = 00. Proširimo funkciju G(w) u Laurentov niz u probušenoj okolini tačke wo = 0: Zbirci na desnoj strani (26.5) predstavljaju regularni i glavni dio proširenja, respektivno. Pređimo na varijablu z, zamjena w = 1/z: Određivanje n= -A*, 6* = 6_„ = s str i primetivši to G(l/z) = f(z), dobijamo Dekompozicija (2G.G) se zove Lorentova ekspanzija funkcije f(z) u probijenoj okolini tačke zq= oo. Prvi zbir u (2G.6) se poziva desni deo, a drugi zbroj je glavni dio ove dekompozicije. Pošto ovi zbroji odgovaraju tačnim i glavnim dijelovima ekspanzije (26.5), onda za proširenje (26.6) vrijede analogi teorema 26.2, 26.3 i 26.6. Dakle, sljedeća teorema će biti analogna teoremi 26.2. Teorema 26.10. Izolovana singularna tačkaZq -
OS (funkcije/(G) je uklonjiv ako i samo ako Laurentova ekspanzija u probijenoj okolini ove tačke ima oblik
t.s. sastoji se samo od ispravnog dijela. Stavimo /(oo) = co. Funkcija definirana nizom (26.7) koji konvergira u susjedstvu z > R tačka 2o = oc, tzv analitički u tački z o = oo. (Imajte na umu da je ova definicija ekvivalentna analitičnosti funkcije G(w) u tački wo = 0.) Primjer 26.11. Istražite singularnu tačku zq = oo funkcije Pošto je granica konačna, onda zo = oo je uklonjiva singularna tačka funkcije /(r). Ako stavimo /(oo) = lim J(z)= 0, onda f(z) postaće analitičan tic u tački Zo= os. Naznačimo kako pronaći odgovarajuću ekspanziju (26.7). Pređimo na varijablu w = 1 fz. Zamena z= 1 /?e, dobijamo (posljednja jednakost vrijedi u probušenom susjedstvu tačke wo = 0, ali ćemo dalje definirati (7(0) = 0). Rezultirajuća funkcija ima singularne tačke w =±i, w =-1/3, i to u tački Wq = 0 je analitičko. Funkcija rasklapanja G(w) po stepenima w(kao što je urađeno u primjeru 25.7) i zamjena u rezultujući niz stepena w = 1/z, možemo dobiti proširenje (26.7) funkcije f(z).
Teorema 26.3 za slučaj zo= oo će biti prepisan u sljedećem obliku. Teorema 26.12. Izolovana singularna tačka th = os funkcija f(z) je pol ako i samo ako je glavni dio Laurentove ekspanzije (26.6) ima samo konačan broj nenultih koeficijenata Sa": Ovdje je niz regularni dio, a polinom u zagradama je glavni dio proširenja. Višestrukost polova u oc definira se kao višestrukost polova wq = 0 funkcija G(z). Lako je vidjeti da se višestrukost pola poklapa s brojem N u (26.8). Q p | (i 2 + 1)(z+3) 2 Zadatak. Pokažite da je funkcija f(z) =--
-- ima unutra tačka zo = oo stub reda 3. Teorema 26.6 o suštinski singularnoj tački može se prepisati za slučaj zo= skoro doslovno, i na tome se ne zadržavamo u detalje.
, uzeti u pozitivnom smjeru duž kružnice L sa centrom u tački z 0 koja leži u domeni analitičnosti funkcije f(z) (tj. u prstenu 0<|z-z0| . (22.15.1)
i odrediti njihov tip.
Učitavanje...
