Oikean ja väärän rationaalisen murtoluvun integrointi. Rationaalisten funktioiden integrointi ja määrittelemättömien kertoimien menetelmä

Murto-rationaalisen funktion integrointi.
Epävarma kerroinmenetelmä

Jatkamme työskentelyä murtolukujen integroimiseksi. Olemme jo tarkastelleet eräiden murtolukutyyppien integraaleja oppitunnilla, ja tätä oppituntia voidaan tietyssä mielessä pitää jatkona. Materiaalin onnistuneeseen ymmärtämiseen tarvitaan perusintegraatiotaitoja, joten jos olet juuri aloittanut integraalien opiskelun, eli olet aloittelija, sinun on aloitettava artikkelista Epämääräinen integraali. Esimerkkejä ratkaisuista.

Kummallista kyllä, nyt emme niinkään etsi integraaleja, vaan... ratkaisemaan lineaarisia yhtälöjärjestelmiä. Tässä suhteessa kiireellisesti Suosittelen osallistumista oppitunnille, nimittäin sinun tulee olla hyvin perehtynyt korvausmenetelmiin ("koulu"-menetelmä ja systeemiyhtälöiden termittäinen yhteenlasku (vähennys)).

Mikä on murto-rationaalinen funktio? Yksinkertaisin sanoin, murto-rationaalinen funktio on murtoluku, jonka osoittaja ja nimittäjä sisältävät polynomeja tai polynomien tuloja. Lisäksi fraktiot ovat kehittyneempiä kuin artikkelissa käsitellyt Joidenkin murtolukujen integrointi.

Oikean murto-rationaalisen funktion integrointi

Välittömästi esimerkki ja tyypillinen algoritmi murto-rationaalisen funktion integraalin ratkaisemiseksi.

Esimerkki 1

Vaihe 1. Ensimmäinen asia, jonka teemme AINA ratkaiseessamme rationaalisen murtofunktion integraalia, on selvittää seuraava kysymys: onko murto oikea? Tämä vaihe suoritetaan suullisesti, ja nyt selitän kuinka:

Ensin katsomme osoittajaa ja selvitämme vanhempi tutkinto polynomi:

Osoittajan johtava teho on kaksi.

Nyt katsomme nimittäjää ja selvitämme vanhempi tutkinto nimittäjä. Ilmeinen tapa on avata sulut ja tuoda samanlaiset termit, mutta voit tehdä sen yksinkertaisemmin jokainen etsi korkein tutkinto suluista

ja kertoa henkisesti: - siis nimittäjän suurin aste on kolme. On aivan selvää, että jos todella avaamme sulut, emme saa kolmea suurempaa astetta.

Johtopäätös: Osoittajan pääaine TIUKASTI on pienempi kuin nimittäjän suurin potenssi, mikä tarkoittaa, että murtoluku on oikea.

Jos tässä esimerkissä osoittaja sisälsi polynomin 3, 4, 5 jne. astetta, murto-osa olisi väärä.

Nyt tarkastellaan vain oikeita murto-osallisia rationaalisia funktioita. Tapausta, jossa osoittajan aste on suurempi tai yhtä suuri kuin nimittäjän aste, käsitellään oppitunnin lopussa.

Vaihe 2. Otetaan nimittäjä kertoimella. Katsotaanpa nimittäjäämme:

Yleisesti ottaen tämä on jo tekijöiden tulos, mutta kuitenkin kysymme itseltämme: onko mahdollista laajentaa jotain muuta? Kidutuksen kohde on epäilemättä neliötrinomi. Päätetään toisen asteen yhtälö:

Diskriminantti on suurempi kuin nolla, mikä tarkoittaa, että trinomi todellakin voidaan kertoa:

Yleissääntö: KAIKKI, mikä VOIDAAN sisällyttää nimittäjään - otamme sen huomioon

Aloitetaan ratkaisun muotoilu:

Vaihe 3. Epämääräisten kertoimien menetelmää käyttämällä laajennetaan integrandi yksinkertaisten (alkeis) murtolukujen summaksi. Nyt se tulee selvemmäksi.

Katsotaanpa integrand-toimintoamme:

Ja tiedätkö, jotenkin herää intuitiivinen ajatus, että olisi mukavaa muuttaa iso murto-osa useaksi pieneksi. Esimerkiksi näin:

Herää kysymys, onko tämä edes mahdollista? Hengitetään helpotuksesta, vastaava lause matemaattinen analyysi väittää - SE ON MAHDOLLISTA. Tällainen hajoaminen on olemassa ja on ainutlaatuinen.

On vain yksi saalis, todennäköisyys on Hei hei Emme tiedä, tästä syystä nimi - määrittelemättömien kertoimien menetelmä.

Kuten arvasit, seuraavat vartalon liikkeet ovat sellaisia, älä kiertele! tarkoituksena on vain TUNNISTAA ne - selvittääkseen, mitä ne vastaavat.

Ole varovainen, selitän yksityiskohtaisesti vain kerran!

Joten aloitetaan tanssiminen:

Vasemmalla puolella vähennämme lausekkeen yhteiseksi nimittäjäksi:

Nyt voimme turvallisesti päästä eroon nimittäjistä (koska ne ovat samat):

Vasemmalla puolella avaamme sulut, mutta älä kosketa tuntemattomia kertoimia toistaiseksi:

Samalla toistetaan koulun sääntö polynomien kertominen. Opettajana opin lausumaan tämän säännön suoralla kasvoilla: Jos haluat kertoa polynomin polynomilla, sinun on kerrottava yhden polynomin jokainen termi toisen polynomin kullakin termillä.

Selkeän selityksen kannalta on parempi laittaa kertoimet suluihin (vaikka en henkilökohtaisesti koskaan tee tätä ajan säästämiseksi):

Muodostamme lineaarisen yhtälöjärjestelmän.
Ensin etsimme vanhempia tutkintoja:

Ja kirjoitamme vastaavat kertoimet järjestelmän ensimmäiseen yhtälöön:

Muista seuraava kohta hyvin. Mitä tapahtuisi, jos oikealla puolella ei olisi yhtään s:tä? Sanotaanko, näyttäytyisikö se ilman neliötä? Tässä tapauksessa järjestelmän yhtälössä olisi tarpeen laittaa nolla oikealle: . Miksi nolla? Mutta koska oikealla puolella voit aina määrittää tämän saman neliön nollalla: Jos oikealla puolella ei ole muuttujia ja/tai vapaata termiä, niin järjestelmän vastaavien yhtälöiden oikealle puolelle laitetaan nollia.

Kirjoitamme vastaavat kertoimet järjestelmän toiseen yhtälöön:

Ja lopuksi, kivennäisvesi, valitsemme ilmaiset jäsenet.

Eh... vitsailin. Vitsit sivuun - matematiikka on vakava tiede. Instituuttiryhmässämme kukaan ei nauranut, kun apulaisprofessori sanoi, että hän hajottaa termit numeroviivalle ja valitsee niistä suurimmat. Ollaanpa tosissaan. Vaikka... joka elää nähdäkseen tämän oppitunnin lopun, hymyilee silti hiljaa.

Järjestelmä on valmis:

Ratkaisemme järjestelmän:

(1) Ensimmäisestä yhtälöstä ilmaistaan ​​ja korvaamme sen järjestelmän 2. ja 3. yhtälöllä. Itse asiassa oli mahdollista ilmaista (tai toinen kirjain) toisesta yhtälöstä, mutta tässä tapauksessa on edullista ilmaista se 1. yhtälöstä, koska pienimmät kertoimet.

(2) Esitämme samanlaiset termit 2. ja 3. yhtälössä.

(3) Lisäämme 2. ja 3. yhtälön termi kerrallaan, jolloin saadaan yhtälö , josta seuraa, että

(4) Korvataan toiseen (tai kolmanteen) yhtälöön, mistä löydämme sen

(5) Korvaa ja ensimmäiseen yhtälöön, jolloin saadaan .

Jos sinulla on vaikeuksia järjestelmän ratkaisumenetelmien kanssa, harjoittele niitä luokassa. Kuinka ratkaista lineaarinen yhtälöjärjestelmä?

Järjestelmän ratkaisemisen jälkeen on aina hyödyllistä tarkistaa - korvata löydetyt arvot joka järjestelmän yhtälö, minkä seurauksena kaiken pitäisi "konvergoida".

Melkein siellä. Kertoimet löydettiin ja:

Valmiin työn pitäisi näyttää suunnilleen tältä:

Kuten näette, tehtävän päävaikeus oli muodostaa (oikein!) ja ratkaista (oikein!) lineaarinen yhtälöjärjestelmä. Ja viimeisessä vaiheessa kaikki ei ole niin vaikeaa: käytämme lineaarisuuden ominaisuuksia epämääräinen integraali ja integroida. Huomaa, että jokaisen kolmen integraalin alla on "ilmainen" monimutkainen toiminto, Puhuin sen integroinnin ominaisuuksista luokassa Muuttujan muutosmenetelmä määrittelemättömässä integraalissa.

Tarkista: Erota vastaus:

Alkuperäinen integrandifunktio on saatu, mikä tarkoittaa, että integraali on löydetty oikein.
Tarkistuksen aikana jouduimme vähentämään lausekkeen yhteiseksi nimittäjäksi, eikä tämä ole sattumaa. Epämääräisten kertoimien menetelmä ja lausekkeen pelkistäminen yhteiseksi nimittäjäksi ovat keskenään käänteisiä toimia.

Esimerkki 2

Etsi epämääräinen integraali.

Palataan murto-osaan ensimmäisestä esimerkistä: . On helppo huomata, että nimittäjässä kaikki tekijät ovat ERI. Herää kysymys, mitä tehdä, jos annetaan esimerkiksi seuraava murto: ? Tässä meillä on asteet nimittäjässä, tai matemaattisesti kerrannaisina. Lisäksi on neliöllinen trinomi, jota ei voida kertoilla (on helppo varmistaa, että yhtälön diskriminantti on negatiivinen, joten trinomia ei voida kertoa). Mitä tehdä? Laajentuminen alkeismurtolukujen summaksi näyttää tältä tuntemattomilla kertoimilla yläosassa vai jotain muuta?

Esimerkki 3

Esittele toiminto

Vaihe 1. Tarkistamme, onko meillä oikea murtoluku
Tärkein osoittaja: 2
Korkein nimittäjä: 8
, mikä tarkoittaa, että murtoluku on oikea.

Vaihe 2. Voiko nimittäjässä huomioida jotain? Ilmeisesti ei, kaikki on jo selvitetty. Neliötrinomia ei voi laajentaa tuotteeksi yllä mainituista syistä. Huppu. Vähemmän työtä.

Vaihe 3. Kuvitellaanpa murto-osainen rationaalinen funktio alkeismurtolukujen summana.
Tässä tapauksessa laajennuksella on seuraava muoto:

Katsotaanpa nimittäjäämme:
Kun murto-rationaalinen funktio jaetaan alkeismurtolukujen summaksi, voidaan erottaa kolme peruspistettä:

1) Jos nimittäjä sisältää "yksinäisen" kertoimen ensimmäiseen potenssiin (tapauksessamme), niin laitamme määräämättömän kertoimen huipulle (tapauksessamme). Esimerkit nro 1, 2 koostuivat vain sellaisista "yksinäisistä" tekijöistä.

2) Jos nimittäjällä on useita kerroin, sinun on hajotettava se seuraavasti:
- eli käy peräkkäin läpi kaikki "X":n asteet ensimmäisestä n:teen asteeseen. Esimerkissämme on kaksi useampaa tekijää: ja , katso vielä kerran antamaani laajennusta ja varmista, että ne on laajennettu täsmälleen tämän säännön mukaisesti.

3) Jos nimittäjä sisältää toisen asteen hajoamattoman polynomin (tässä tapauksessamme), niin osoittajassa hajottaessa sinun on kirjoitettava lineaarinen funktio epävarmilla kertoimilla (tässä tapauksessa epävarmilla kertoimilla ja ).

Itse asiassa on toinenkin neljäs tapaus, mutta vaikenen siitä, koska käytännössä se on erittäin harvinaista.

Esimerkki 4

Esittele toiminto tuntemattomien kertoimien alkeisosien summana.

Tämä on esimerkki itsenäinen päätös. Koko ratkaisu ja vastaus oppitunnin lopussa.
Noudata tarkasti algoritmia!

Jos ymmärrät periaatteet, joiden mukaan sinun on laajennettava murto-rationaalinen funktio summaksi, voit pureskella läpi melkein minkä tahansa tarkasteltavana olevan tyypin integraalin.

Esimerkki 5

Etsi epämääräinen integraali.

Vaihe 1. Ilmeisesti murtoluku on oikea:

Vaihe 2. Voiko nimittäjässä huomioida jotain? Voi. Tässä on kuutioiden summa . Kerro nimittäjä lyhennetyn kertolaskukaavan avulla

Vaihe 3. Epämääräisten kertoimien menetelmää käyttämällä laajennamme integrandin alkeismurtolukujen summaksi:

Huomaa, että polynomia ei voi kertoilla (tarkista, että diskriminantti on negatiivinen), joten laitamme yläosaan lineaarifunktion tuntemattomilla kertoimilla, ei vain yhtä kirjainta.

Tuomme murto-osan yhteiseen nimittäjään:

Laaditaan ja ratkaistaan ​​järjestelmä:

(1) Esitämme ensimmäisestä yhtälöstä ja korvaamme sen järjestelmän toisella yhtälöllä (tämä on järkevin tapa).

(2) Esitämme samanlaiset termit toisessa yhtälössä.

(3) Lisäämme järjestelmän toisen ja kolmannen yhtälön termi kerrallaan.

Kaikki muut laskelmat ovat periaatteessa suullisia, koska järjestelmä on yksinkertainen.

(1) Kirjoitetaan murto-osien summa löydettyjen kertoimien mukaisesti.

(2) Käytämme epämääräisen integraalin lineaarisuusominaisuuksia. Mitä toisessa integraalissa tapahtui? Voit tutustua tähän menetelmään oppitunnin viimeisessä kappaleessa. Joidenkin murtolukujen integrointi.

(3) Jälleen kerran käytämme lineaarisuuden ominaisuuksia. Kolmannessa integraalissa alamme eristää koko neliön (oppitunnin toiseksi viimeinen kappale Joidenkin murtolukujen integrointi).

(4) Otamme toisen integraalin, kolmannessa valitsemme koko neliön.

(5) Otetaan kolmas integraali. Valmis.

Rationaalinen funktio on muodon murto-osa, jonka osoittaja ja nimittäjä ovat polynomeja tai polynomien tuloja.

Esimerkki 1. Vaihe 2.

.

Kerromme määrittelemättömät kertoimet polynomeilla, jotka eivät ole tässä yksittäisessä murtoluvussa, mutta jotka ovat muissa tuloksena olevissa murtoluvuissa:

Avaamme sulut ja rinnastamme alkuperäisen integrandin osoittajan tuloksena olevaan lausekkeeseen:

Yhtälön molemmilta puolilta etsimme termejä, joilla on samat x:n potenssit, ja muodostamme niistä yhtälöjärjestelmän:

.

Perutaan kaikki x:t ja saadaan vastaava yhtälöjärjestelmä:

.

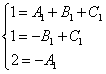Siten integrandin lopullinen laajennus summaksi yksinkertaisia ​​murtolukuja:

.

Esimerkki 2. Vaihe 2. Vaiheessa 1 saimme seuraavan jaottelun alkuperäisestä murtoluvusta yksinkertaisten murtolukujen summaksi, joiden kertoimia osoittajissa ei ole määritetty:

.

Nyt aletaan etsiä epävarmoja kertoimia. Tätä varten vertaamme funktiolausekkeen alkuperäisen murtoluvun osoittajaa sen lausekkeen osoittajaan, joka saadaan, kun murto-osien summa on vähennetty yhteiseksi nimittäjäksi:

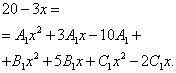
Nyt sinun on luotava ja ratkaistava yhtälöjärjestelmä. Tätä varten vertaamme muuttujan kertoimet vastaavaan asteeseen funktion alkuperäisen lausekkeen osoittajassa ja vastaavat kertoimet edellisessä vaiheessa saadussa lausekkeessa:

Ratkaisemme tuloksena olevan järjestelmän:

Joten täältä

.

Esimerkki 3. Vaihe 2. Vaiheessa 1 saimme seuraavan jaottelun alkuperäisestä murtoluvusta yksinkertaisten murtolukujen summaksi, joiden kertoimia osoittajissa ei ole määritetty:

Alamme etsiä epävarmoja kertoimia. Tätä varten vertaamme funktiolausekkeen alkuperäisen murtoluvun osoittajaa sen lausekkeen osoittajaan, joka saadaan, kun murto-osien summa on vähennetty yhteiseksi nimittäjäksi:

Kuten aiemmissa esimerkeissä, muodostamme yhtälöjärjestelmän:

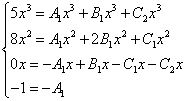
Vähennämme x:t ja saamme vastaavan yhtälöjärjestelmän:

Ratkaisemalla järjestelmän saamme seuraavat epävarmojen kertoimien arvot:

Saamme integrandin lopullisen hajotuksen yksinkertaisten murtolukujen summaksi:

.

Esimerkki 4. Vaihe 2. Vaiheessa 1 saimme seuraavan jaottelun alkuperäisestä murtoluvusta yksinkertaisten murtolukujen summaksi, joiden kertoimia osoittajissa ei ole määritetty:

.

Tiedämme jo aikaisemmista esimerkeistä, kuinka alkuperäisen murtoluvun osoittaja rinnastetaan osoittajassa olevaan lausekkeeseen, joka saadaan, kun murto on hajotettu yksinkertaisten murtolukujen summaksi ja tuotu tämä summa yhteiseen nimittäjään. Siksi vain ohjaustarkoituksiin esitämme tuloksena olevan yhtälöjärjestelmän:

Ratkaisemalla järjestelmän saamme seuraavat epävarmojen kertoimien arvot:

Saamme integrandin lopullisen hajotuksen yksinkertaisten murtolukujen summaksi:

Esimerkki 5. Vaihe 2. Vaiheessa 1 saimme seuraavan jaottelun alkuperäisestä murtoluvusta yksinkertaisten murtolukujen summaksi, joiden kertoimia osoittajissa ei ole määritetty:

.

Vähennämme tämän summan itsenäisesti yhteiseksi nimittäjäksi ja rinnastamme tämän lausekkeen osoittajan alkuperäisen murtoluvun osoittajaan. Tuloksena pitäisi olla seuraava yhtälöjärjestelmä:

Ratkaisemalla järjestelmän saamme seuraavat epävarmojen kertoimien arvot:

.

Saamme integrandin lopullisen hajotuksen yksinkertaisten murtolukujen summaksi:

.

Esimerkki 6. Vaihe 2. Vaiheessa 1 saimme seuraavan jaottelun alkuperäisestä murtoluvusta yksinkertaisten murtolukujen summaksi, joiden kertoimia osoittajissa ei ole määritetty:

Suoritamme samat toiminnot tällä määrällä kuin edellisissä esimerkeissä. Tuloksena pitäisi olla seuraava yhtälöjärjestelmä:

Ratkaisemalla järjestelmän saamme seuraavat epävarmojen kertoimien arvot:

.

Saamme integrandin lopullisen hajotuksen yksinkertaisten murtolukujen summaksi:

.

Esimerkki 7. Vaihe 2. Vaiheessa 1 saimme seuraavan jaottelun alkuperäisestä murtoluvusta yksinkertaisten murtolukujen summaksi, joiden kertoimia osoittajissa ei ole määritetty:

.

Tiettyjen toimien jälkeen tuloksena olevalla määrällä tulisi saada seuraava yhtälöjärjestelmä:

Ratkaisemalla järjestelmän saamme seuraavat epävarmojen kertoimien arvot:

Saamme integrandin lopullisen hajotuksen yksinkertaisten murtolukujen summaksi:

.

Esimerkki 8. Vaihe 2. Vaiheessa 1 saimme seuraavan jaottelun alkuperäisestä murtoluvusta yksinkertaisten murtolukujen summaksi, joiden kertoimia osoittajissa ei ole määritetty:

.

Tehdään joitakin muutoksia toimiin, jotka on jo saatettu automaattisiksi yhtälöjärjestelmän saamiseksi. On olemassa keinotekoinen tekniikka, joka auttaa joissakin tapauksissa välttämään tarpeettomia laskelmia. Tuomalla murto-osien summa yhteiseen nimittäjään, saamme ja rinnastamalla tämän lausekkeen osoittajan alkuperäisen murtoluvun osoittajaan, saamme.

Aiemmin keskustelimme yleisistä integraatiomenetelmistä. Tässä ja seuraavissa kappaleissa puhumme tiettyjen funktioluokkien integroinnista käsiteltyjen tekniikoiden avulla.

Yksinkertaisimpien rationaalisten funktioiden integrointi

Tarkastellaan muodon integraalia \textstyle(\int R(x)\,dx), jossa y=R(x) on rationaalinen funktio. Mikä tahansa rationaalinen lauseke R(x) voidaan esittää muodossa \frac(P(x))(Q(x)), jossa P(x) ja Q(x) ovat polynomeja. Jos tämä murtoluku on virheellinen, eli jos osoittajan aste on suurempi tai yhtä suuri kuin nimittäjän aste, se voidaan esittää polynomin summana ( koko osa) ja oikea murto-osa. Siksi riittää, kun harkitaan oikeiden murtolukujen integrointia.

Osoitetaan, että tällaisten jakeiden integrointi pelkistyy integraatioon yksinkertaisia ​​murtolukuja, eli muodon ilmaisuja:

\mathsf(1))~\frac(A)(x-a);\quad \mathsf(2))~\frac(A)((x-a)^n);\quad \mathsf(3))~ \frac( Ax+B)(x^2+px+q);\quad \mathsf(4))~\frac(Ax+B)((x^2+px+q)^n).

Missä A,\,B,\,a,\,p,\,q ovat reaalilukuja, ja neliötrinomilla x^2+px+q ei ole todellisia juuria. Tyypin 1) ja 2) lausekkeita kutsutaan 1. tyypin murtoluvuiksi, ja tyypin 3) ja 4) lausekkeita kutsutaan 2. tyypin murtoluvuiksi.

Ensimmäisen tyypin murtolukujen integraalit lasketaan suoraan

\begin(tasattu)\mathsf(1))&~\int\frac(A)(x-a)\,dx= A\ln|x-a|+C;\\ \mathsf(2))&~ \int\frac (A)((x-a)^n)\,dx= A\int(x-a)^(-n)\,dx= A\,\frac((x-a)^(-n+1))(-n+ 1 )+C~(n=2,3,4,\ldots). \end(tasattu)

Tarkastellaan 2. tyypin murto-osien integraalien laskentaa: \mathsf(3))~ \int\frac(Ax+B)(x^2+px+q)\,dx\,.

Ensin panemme merkille sen

\int\frac(dt)(t^2+a^2)= \frac(1)(a)\operaattorinimi(arctg)\frac(t)(a)+C,\qquad \int\frac(t\ ,dt)(t^2+a^2)= \frac(1)(2)\ln(t^2+a^2)+C.

Integraalin 3) laskemisen pelkistämiseksi näihin kahteen integraaliin muunnetaan neliötrinomi x^2+px+q erottamalla siitä täydellinen neliö:

x^2+px+q= (\left(x+\frac(p)(2)\right)\^2+ \left(q-\frac{p^2}{4}\right)\!. !}

Koska olettaen, että tällä trinomilla ei ole todellisia juuria q-\frac(p^2)(4)>0 ja voimme laittaa q-\frac(p^2)(4)=a^2. Korvaus x+\frac(p)(2)=t,~ dx=dt muuntaa integraalin 3) mainitun kahden integraalin lineaariseksi yhdistelmäksi:

\begin(tasattu)\int\frac(Ax+B)(x^2+px+q)\,dx&= \int\frac(A\!\left(t-\frac(p)(2)\right )+B)(t^2+a^2)\,dt= A\int\frac(t\,dt)(t^2+a^2)+ \left(B-\frac(Ap)(2 )\right)\!\int\frac(dt)(t^2+a^2)=\\ &=\frac(A)(2)\ln(t^2+a^2)+ \frac( 1)(a)\!\left(B-\frac(Ap)(2)\oikea)\!\ \operaattorinimi(arctg)\frac(t)(a)+C. \end(tasattu)

Lopullisessa vastauksessa sinun tarvitsee vain korvata (t) x+\frac(p)(2) ja (a) \sqrt(q-\frac(p^2)(4)). Koska t^2+a^2=x^2+px+q, niin

\int\frac(Ax+B)(x^2+px+q)\,dx= \frac(A)(2)\ln(x^2+px+q)+ \frac(B-\dfrac( Ap)(2))(\sqrt(q-\dfrac(p^2)(4))) \operaattorinimi(arctg)\frac(x+\dfrac(p)(2))(\sqrt(q-\dfrac) (p^2)(4)))+C.

Harkitse tapausta \mathsf(4))~ \int\frac(Ax+B)((x^2+px+q)^n)\,dx.

Kuten edellisessä tapauksessa, asetetaan x+\frac(p)(2)=t. Saamme:

\int\frac(Ax+B)((x^2+px+q)^n)\,dx= A\int\frac(t\,dt)((t^2+a^2)^n) + \left(B-\frac(Ap)(2)\oikea)\! \int\frac(dt)((t^2+a^2)^n)\,.

Ensimmäinen termi lasketaan seuraavasti:

A\int\frac(t\,dt)((t^2+a^2)^n)= \frac(A)(2)\int(t^2+a^2)^(-n)\ ,d(t^2+a^2)= \frac(A)(2)\frac((t^2+a^2)^(-n+1))(-n+1)= \frac( A)(2(1-n)(t^2+a^2)^(n-1))\,.

Toinen integraali lasketaan käyttämällä toistuvuuskaavaa.

Esimerkki 1. Lasketaan \int\frac(3x+2)(x^2+2x+3)\,dx.

Ratkaisu. Meillä on: x^2+2x+3=(x+1)^2+2. Laitetaan x+1=t. Sitten dx=dt ja 3x+2=3(t-1)+2=3t-1 ja siksi

\begin(tasattu)\int\frac(3x+2)(x^2+2x+3)\,dx&= \int\frac(3t-1)(t^2+2)\,dt= \frac( 3)(2)\int\frac(2t\,dt)(t^2+2)- \int\frac(dt)(t^2+(\sqrt(2))^2)=\\ &= \frac(3)(2)\ln(t^2+2)- \frac(1)(\sqrt(2))\operaattorinimi(arctg)\frac(t)(\sqrt(2))+C= \\ &=\frac(3)(2)\ln(x^2+2x+3)- \frac(1)(\sqrt(2))\operaattorinimi(arctg)\frac(x+1)(\ sqrt(2))+C. \end(tasattu)

Esimerkki 2. Lasketaan \int\frac(x+2)((x^2+6x+10)^2)\,dx.

Ratkaisu. Meillä on: x^2+6x+10=(x+3)^2+1. Otetaan käyttöön uusi muuttuja asettamalla x+3=t. Sitten dt=dx ja x+2=t-1. Korvaamalla muuttujan integraalimerkin alla, saamme:

\begin(tasattu)\int\frac(x+2)((x^2+6x+10)^2)\,dx&= \int\frac(t-1)((t^2+1)^2 )\,dt= \frac(1)(2)\int\frac(2t\,dt)((t^2+1)^2)-\int\frac(dt)((t^2+1) ^2)=\\ &=-\frac(1)(2(t^2+1))- \int\frac(dt)((t^2+1)^2)\,. \end(tasattu))

Laitetaan I_2=\int\frac(dt)((t^2+1)^2). Meillä on:

I_2=\frac(1)(2)I_1+\frac(1)(2)\frac(t)(t^2+1), Mutta I_1=\int\frac(dt)(t^2+1)= \operaattorinimi(arctg)t Täten, I_2= \frac(1)(2)\operaattorinimi(arctg)t+ \frac(t)(2(t^2+1)).

Lopulta saamme:

\begin(tasattu)\int\frac(x+2)((x^2+6x+10)^2)\,dx&=-\frac(1)(2(t^2+1))-\frac (1)(2)\operaattorinnimi(arctg)t-\frac(t)(2(t^2+1))=\\ &=-\frac(1)(2(x^2+6x+10) )- \frac(1)(2)\operaattorinimi(arctg)(x+3)- \frac(x+3)(2(x^2+6x+10))+C=\\ &=\frac( -x-4)(2(x^2+6x+10))-\frac(1)(2)\operaattorin nimi(arctg)(x+3)+C \end(tasattu)

Oikeiden murtolukujen integrointi

Harkitse oikeaa murtolukua R(x)=\frac(P(x))(Q(x)), missä Q(x) on n-asteinen polynomi. Yleisyyden menettämättä voidaan olettaa, että Q(x):n johtava kerroin on yhtä suuri kuin 1. Algebran kurssilla todistetaan, että tällainen polynomi, jolla on reaalikertoimet, voidaan faktoroida ensimmäisen ja toisen asteen tekijöiksi reaalikertoimilla. :

Q(x)= (x-x_1)^(\alpha)\lpisteet (x-x_k)^(\beta) (x^2+p\,x+q)^(\gamma)\lpisteet (x^2) +r\,x+s)^(\delta).

missä x_1,\lpisteet,x_k ovat polynomin Q(x) todelliset juuret ja neliötrinomeilla ei ole todellisia juuria. Voidaan todistaa, että silloin R(x) esitetään muodon 1) -4 yksinkertaisten murtolukujen summana):

\begin(tasattu)R(x)=&\frac(P(x))(Q(x))= \frac(A_1)((x-x_1)^(\alpha))+ \frac(A_2)( (x-x_1)^(\alpha-1))+\ldots+ \frac(A_(\alpha))(x-x_1)\,+\\ &+\,\ldots+ \frac(B_1)((x- x_k)^(\beta))+ \frac(B_2)((x-x_k)^(\beta-1))+\ldots+ \frac(B_(\beta))(x-x_k)+ \frac(M_1x+ N_1)((x^2+p\,x+q)^(\gamma))\,+\\ &+\,\ldots+ \frac(M_(\gamma)+ N_(\gamma))(x^ 2+ p\,x+s)+ \frac(E_1x+F_1)((x^2+rx+s)^(\delta))+\ldots+ \frac(E_(\delta)x+F_(\delta ))(x^2+rx+s)\, \end(tasattu)

jossa nimittäjien eksponentit pienenevät peräkkäin \alphasta 1:ksi, ..., \betasta 1:ksi, \gammasta 1:ksi, ..., \deltasta 1:ksi ja A_1,\ldots,F_(\delta)- epävarmat kertoimet. Näiden kertoimien löytämiseksi on tarpeen päästä eroon nimittäjistä ja kahden polynomin yhtäläisyyden saatuaan käyttää epämääräisten kertoimien menetelmää.

Toinen tapa määrittää kertoimet A_1,\ldots, A_(\alpha), \ldots, F_(\delta) perustuu muuttujan x arvojen korvaamiseen. Korvaamalla minkä tahansa luvun x:n sijasta yhtälöstä (1) saatuun yhtälöön nimittäjien eliminoinnin jälkeen, päädymme lineaarinen yhtälö suhteessa vaadittuihin kertoimiin. Korvaamalla tarvittava määrä tällaisia ​​muuttujan osaarvoja, saadaan yhtälöjärjestelmä kertoimien löytämiseksi. Muuttujan yksityisiksi arvoiksi on kätevintä valita nimittäjän juuret (sekä todelliset että kompleksiset). Tässä tapauksessa lähes kaikki yhtälön oikealla puolella olevat termit (eli kahden polynomin yhtäläisyys) katoavat, mikä helpottaa jäljellä olevien kertoimien löytämistä. Kun korvaat kompleksiarvoja, muista, että kaksi kompleksilukua ovat yhtä suuret, jos ja vain, jos niiden reaali- ja imaginaariosa ovat samat. Siksi jokaisesta yhtälöstä, joka sisältää kompleksilukuja, saadaan kaksi yhtälöä.

Kun määrittelemättömät kertoimet on löydetty, on jäljellä laskea saatujen yksinkertaisimpien murtolukujen integraalit. Koska integroitaessa yksinkertaisimpia murtolukuja, kuten olemme nähneet, saadaan vain rationaaliset funktiot, arktangentit ja logaritmit, niin minkä tahansa rationaalisen funktion integraali ilmaistaan ​​rationaalifunktion, arktangenttien ja logaritmien kautta.

Esimerkki 3. Lasketaan oikean rationaalisen murtoluvun integraali \int\frac(6x+1)(x^2+2x-3)\,dx.

Ratkaisu. Kerrotaan integrandin nimittäjä:

x^2+2x-3=(x-1)(x+3).

Kirjoitetaan integrandi ja esitetään se yksinkertaisten murtolukujen summana:

\frac(6x+1)(x^2+2x-3)= \frac(A)(x-1)+\frac(B)(B+3)\,.

6x+1=A\cpiste (x+3)+B\cpiste (x-1)\,.

Kertoimien löytämiseksi käytämme osittaisten arvojen korvausmenetelmää. Löytääksesi kertoimen A, asetetaan x=1. Sitten yhtälöstä (2) saadaan 7=4A, josta A=7/4. Löytääksesi kertoimen B, asetetaan x=-3. Sitten yhtälöstä (2) saadaan -17=-4B, josta B=17/4.

Niin, \frac(6x+1)(x^2+2x-3)= \frac(7)(4)\cdot\frac(1)(x-1)+ \frac(17)(4)\cdot\frac (1)(x+3). tarkoittaa,

\int\frac(6x+1)(x^2+2x-3)\,dx= \frac(7)(4)\int\frac(dx)(x-1)+ \frac(17)(4 )\int\frac(dx)(x+3)= \frac(7)(4)\ln|x-1|+ \frac(17)(4)\ln|x+3|+C.

Esimerkki 4. Lasketaan \int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx.

Ratkaisu. Kirjoitetaan integrandi ja esitetään se yksinkertaisten murtolukujen summana. Nimittäjä sisältää tekijän x^2+2, jolla ei ole todellisia juuria, vaan se vastaa murto-osaa 2. lajista: \frac(Ax+B)(x^2+2) kerroin (x-1)^2 vastaa kahden ensimmäisen lajin murto-osan summaa: \frac(C)((x-1)^2)+ \frac(D)(x-1); lopuksi tekijä x+2 vastaa yhtä murto-osaa 1. lajista \frac(E)(x+2) . Siten esitämme integrandifunktion neljän murtoluvun summana:

\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(Ax+B)(x^2+2 )+ \frac(C)((x-1)^2)+ \frac(D)(x-1)+ \frac(E)(x+2)\,.

\begin(tasattu) x^4+2x^2+8x+5&= (Ax+B)(x-1)^2(x+2)+ C(x^2+2)(x+2)\, +\\ &\phantom(=)+ D(x^2+2)(x-1)(x+2)+ E(x^2+2)(x-1)^2.\end(tasattu)

Integrandin nimittäjällä on kaksi reaalijuurta: x=1 ja x=-2. Kun arvo x=1 korvataan yhtälöllä (4), saadaan 16=9C, josta saadaan C=16/9. Korvaamalla x=-2 saamme 13=54E ja määritämme vastaavasti E=13/54. Korvaamalla arvon x=i\,\sqrt(2) (polynomin x^2+2 juuri) pääsemme tasa-arvoon

4-4+8\,i\,\sqrt(2)+5= (A\,i\,\sqrt(2)+B)\cdot (i\,\sqrt(2)-1)^2\ cdot (i\,\sqrt(2)+2).

Se muuttuu muotoon:

(10A+2B)+(2A-5B)\sqrt(2)\,i= 5+8\sqrt(2)\,i, josta 10A+2B=5 ja (2A-5B)\sqrt(2)=8\sqrt(2).

Kahden yhtälöjärjestelmän ratkaiseminen kahdella muuttujalla \begin(tapaukset)10A+2B=5,\\ 2A-5B=8,\end(tapaukset) löydämme: A=\frac(41)(54),~ B=-\frac(35)(27).

On vielä määritettävä kertoimen D arvo. Avataan tätä varten yhtälön (4) sulut, esitetään samanlaiset termit ja verrataan sitten x^4:n kertoimia. Saamme:

A+D+E=1, eli D=0.

Korvataan kertoimien löydetyt arvot yhtälöön (3):

\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(\drac(41)(54)\, x- \dfrac(35)(27))(x^2+2)+ \frac(16)(9)\frac(1)((x-1)^2)+ \frac(13)(54) \frac(1)(x+2)\,

\begin(tasattu)\int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx&= \frac( 41)(54)\int\frac(x\,dx)(x^2+2)- \frac(35)(27)\int\frac(dx)(x^2+2)+ \frac(16) )(9) \int\frac(dx)((x-1)^2)+ \frac(13)(54)\int\frac(dx)(x+2)=\\ &=\frac(41) )(108)\ln(x^2+2)- \frac(35)(27\sqrt(2))\operaattorinimi(arctg)\frac(x)(\sqrt(2))- \frac(16) (9(x-1))+ \frac(13)(54) \ln|x+2|+C.\end(tasattu)

Integroi vääriä murtolukuja

Oletetaan, että meidän on integroitava toiminto y=\frac(f(x))(g(x)), jossa f(x) ja g(x) ovat polynomeja ja polynomin f(x) aste on suurempi tai yhtä suuri kuin polynomin g(x) aste. Tässä tapauksessa sinun on ensin valittava koko osa väärä murtoluku \frac(f(x))(g(x)), eli edustaa sitä muodossa

\frac(f(x))(g(x))=s(x)+ \frac(r(x))(g(x))\,

missä s(x) on polynomi, jonka aste on yhtä suuri kuin polynomien f(x) ja g(x) asteiden välinen ero, ja \frac(r(x))(g(x))- oikea murto-osa.

Sitten meillä on \int\frac(f(x))(g(x))\,dx= \int s(x)\,dx+ \int\frac(r(x))(g(x))\,dx\, ..

Esimerkki 5. Lasketaan väärän murtoluvun integraali \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx.

Ratkaisu. Meillä on:

\begin(tasattu)g(x)&=(x-1)(x+2)(x-3)= x^3-2x^2-5x+6,\\ f(x)&=x^4 -4x^3+x^2+16x-11. \end(tasattu)

Eristääksesi koko osan, jaa f(x) g(x):llä: \frac(f(x))(g(x))= x-2+\frac(2x^2+1)(x^3-2x^2-5x+6)\,.

tarkoittaa, \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx= \int(x-2)dx+ \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx

Meillä on: \int(x-2)dx=\frac(x^2)(2)-2x+C.

Integraalin laskemiseen \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx Käytetään määrittelemättömien kertoimien menetelmää, kuten edellä. Laskelmien jälkeen, jotka jätämme lukijalle, saamme.

AIHE: Integraatio rationaaliset murtoluvut.

Huomio! Kun tutkitaan yhtä integroinnin perusmenetelmiä: rationaalisten murtolukujen integrointia, on otettava huomioon kompleksialueen polynomit tiukkojen todisteiden suorittamiseksi. Siksi se on välttämätöntä opiskella etukäteen jotkin kompleksilukujen ominaisuudet ja operaatiot niillä.

Yksinkertaisten rationaalisten murtolukujen integrointi.

Jos P(z) Ja K(z) ovat polynomeja kompleksialueella, niin ne ovat rationaalisia murtolukuja. Sitä kutsutaan oikea, jos tutkinto P(z) vähemmän tutkintoa K(z) , Ja väärä, jos tutkinto R vähintään tutkinnon K.

Mikä tahansa väärä murtoluku voidaan esittää seuraavasti: ,

P(z) = Q(z) S(z) + R(z),

a R(z) – polynomi, jonka aste on pienempi kuin aste K(z).

Siten rationaalisten murtolukujen integrointi laskee polynomien eli potenssifunktioiden ja oikeiden murtolukujen integrointiin, koska se on oikea murtoluku.

Määritelmä 5. Yksinkertaisimmat (tai alkeis-) murtoluvut ovat seuraavan tyyppisiä murtolukuja:

1) , 2) , 3) , 4) .

Selvitetään, kuinka ne integroituvat.

3) (tutkittu aiemmin).

Lause 5. Jokainen oikea murtoluku voidaan esittää yksinkertaisten murtolukujen summana (ilman todistetta).

Johtopäätös 1. Jos on oikea rationaalinen murtoluku ja jos polynomin juurien joukossa on vain yksinkertaisia ​​reaalijuuria, niin murto-osan hajotuksessa yksinkertaisten murtolukujen summaksi tulee vain ensimmäisen tyypin yksinkertaisia ​​murto-osia:

Esimerkki 1.

Johtopäätös 2. Jos on oikea rationaalinen murto ja jos polynomin juurien joukossa on vain useita reaalijuuria, niin murto-osan hajotuksessa yksinkertaisten murtolukujen summaksi tulee vain 1. ja 2. tyypin yksinkertaisia ​​murtolukuja :

Esimerkki 2.

Johtopäätös 3. Jos on oikea rationaalinen murtoluku ja jos polynomin juurien joukossa on vain yksinkertaisia ​​kompleksisia konjugaattijuuria, niin murto-osan hajotuksessa yksinkertaisten murtolukujen summaksi tulee vain 3. tyypin yksinkertaisia ​​murto-osia:

Esimerkki 3.

Johtopäätös 4. Jos on oikea rationaalinen murto ja jos polynomin juurien joukossa on vain useita kompleksisia konjugaattijuuria, niin murto-osan hajotuksessa yksinkertaisten murtolukujen summaksi on vain 3. ja 4. tyypit:

Tuntemattomien kertoimien määrittämiseksi annetuissa laajennuksissa toimi seuraavasti. Tuntemattomia kertoimia sisältävän laajennuksen vasen ja oikea puoli kerrotaan. Saadaan kahden polynomin yhtäläisyys. Siitä saadaan yhtälöt vaadituille kertoimille käyttämällä:

1. yhtäläisyys on totta kaikille X:n arvoille (osittaisarvomenetelmä). Tässä tapauksessa saadaan mikä tahansa määrä yhtälöitä, joista mikä tahansa m mahdollistaa tuntemattomien kertoimien löytämisen.

2. kertoimet ovat yhteneväisiä samoilla X:n asteikoilla (epämääräisten kertoimien menetelmä). Tässä tapauksessa saadaan m - yhtälöjärjestelmä m - tuntemattomien kanssa, josta tuntemattomat kertoimet löydetään.

3. yhdistetty menetelmä.

Esimerkki 5. Laajenna murto-osa yksinkertaisimpaan.

Ratkaisu:

Etsitään kertoimet A ja B.

Tapa 1 – yksityisen arvon menetelmä:

Menetelmä 2 – määrittelemättömien kertoimien menetelmä:

Vastaus:

Rationaalisten murtolukujen integrointi.

Lause 6. Minkä tahansa rationaalisen murtoluvun määrittelemätön integraali millä tahansa välillä, jolla sen nimittäjä ei ole nolla, on olemassa ja se ilmaistaan ​​alkeisfunktioilla, nimittäin rationaalisilla murtoluvuilla, logaritmeilla ja arctangenteilla.

Todiste.

Kuvitellaan rationaalinen murto-osa muodossa: . Tässä tapauksessa viimeinen termi on oikea murtoluku ja Lauseen 5 mukaan se voidaan esittää yksinkertaisten murtolukujen lineaarisena yhdistelmänä. Siten rationaalisen murtoluvun integrointi pelkistyy polynomin integraatioksi S(x) ja yksinkertaiset jakeet, joiden antiderivaatteilla, kuten on esitetty, on lauseessa osoitettu muoto.

Kommentti. Suurin vaikeus tässä tapauksessa on nimittäjän hajottaminen tekijöiksi, eli kaikkien sen juurien etsiminen.

Esimerkki 1. Etsi integraali