Théorème. Laissez la fonction x=φ(t) continu en un point un, et la fonction y=f(x) continu en un point b = φ (une). Alors la fonction complexe y=f[φ(t)]=F(t) continu en un point un.

Laisser x=φ(t) Et y=f(x)- les fonctions élémentaires les plus simples, avec de nombreuses valeurs (X) les fonctions x=φ(t) est la portée de la fonction y=f(x). Comme nous le savons, les fonctions élémentaires sont continues en tout point du domaine donné. Donc, d’après le théorème précédent, la fonction complexe y=f(φ(t)), c'est-à-dire la superposition de deux fonctions élémentaires, est continue. Par exemple, une fonction est continue en tout point x ≠ 0, comme fonction complexe de deux fonctions élémentaires x=t-1 Et y = péché x. Fonctionne également y=ln péché x continue en tout point dans les intervalles (2kπ,(2k+1)π), k ∈Z (péché x>0).

Définition
Fonction f (X) appelé continu au point x 0 voisinage de ce point, et si la limite lorsque x tend vers x 0 égal à la valeur de la fonction en x 0 :
.

En utilisant les définitions de Cauchy et Heine de la limite d’une fonction, nous pouvons donner définitions élargies de la continuité d'une fonction en un point .

Nous pouvons formuler le concept de continuité dans en termes d'incréments. Pour ce faire, nous introduisons une nouvelle variable, appelée l'incrément de la variable x au point. Alors la fonction est continue au point si
.
Introduisons une nouvelle fonction :
.
Ils l'appellent incrément de fonction au point . Alors la fonction est continue au point si
.

Définition de la continuité à droite (gauche)
Fonction f (X) appelé continue à droite (gauche) au point x 0 , s'il est défini sur un voisinage droit (gauche) de ce point, et si la limite droite (gauche) au point x 0 égal à la valeur de la fonction en x 0 :
.

Théorème sur le caractère limité d'une fonction continue
Soit la fonction f (X) est continue au point x 0 . Alors il y a un quartier U (x0), sur lequel la fonction est limitée.

Théorème sur la préservation du signe d'une fonction continue
Soit la fonction continue au point. Et laissez-le avoir une valeur positive (négative) à ce stade :
.
Il existe alors un voisinage du point où la fonction a une valeur positive (négative) :
à .

Propriétés arithmétiques des fonctions continues
Laissez les fonctions et être continues au point .
Alors les fonctions , et sont continues au point .
Si , alors la fonction est continue au point .

Propriété de continuité gauche-droite
Une fonction est continue en un point si et seulement si elle est continue à droite et à gauche.

Des preuves des propriétés sont données sur la page « Propriétés des fonctions continues en un point ».

Continuité d'une fonction complexe

Théorème de continuité pour une fonction complexe
Soit la fonction continue au point. Et que la fonction soit continue au point.
Alors la fonction complexe est continue en ce point.

Limite d'une fonction complexe

Théorème sur la limite d'une fonction continue d'une fonction
Soit une limite de la fonction en , et elle est égale à :
.
Voici le point t 0 peut être fini ou infiniment distant : .
Et que la fonction soit continue au point.
Alors il existe une limite d’une fonction complexe, et elle est égale à :
.

Théorème sur la limite d'une fonction complexe
Laissez la fonction avoir une limite et mappez un voisinage perforé d'un point sur un voisinage perforé d'un point. Laissez la fonction être définie sur ce quartier et ayez une limite sur celui-ci.
Voici les points finaux ou infiniment éloignés : . Les quartiers et leurs limites correspondantes peuvent être bilatéraux ou unilatéraux.
Alors il existe une limite d’une fonction complexe et elle est égale à :
.

Points de rupture

Détermination du point de rupture
Laissez la fonction être définie sur un voisinage perforé du point. Le point s'appelle point d'arrêt de fonction, si l'une des deux conditions suivantes est remplie :
1) non défini dans ;
2) est défini en , mais ne l'est pas à ce stade.

Détermination du point de discontinuité de 1ère espèce
Le point s'appelle point de discontinuité du premier type, if est un point de rupture et il y a des limites unilatérales finies à gauche et à droite :
.

Définition d'un saut de fonction
Fonction de saut Δ en un point est la différence entre les limites à droite et à gauche
.

Détermination du point de rupture
Le point s'appelle point de rupture amovible, s'il y a une limite
,
mais la fonction en ce point soit n'est pas définie, soit n'est pas égale à la valeur limite : .

Ainsi, le point de discontinuité amovible est le point de discontinuité de 1ère espèce, auquel le saut de la fonction est égal à zéro.

Détermination du point de discontinuité du 2ème type
Le point s'appelle point de discontinuité du deuxième type, s'il ne s'agit pas d'un point de discontinuité de 1ère espèce. Autrement dit, s’il n’y a pas au moins une limite unilatérale, ou au moins une limite unilatérale en un point est égale à l’infini.

Propriétés des fonctions continues sur un intervalle

Définition d'une fonction continue sur un intervalle
Une fonction est dite continue sur un intervalle (at) si elle est continue en tous points de l'intervalle ouvert (at) et aux points a et b, respectivement.

Premier théorème de Weierstrass sur le caractère borné d'une fonction continue sur un intervalle
Si une fonction est continue sur un intervalle, alors elle est bornée sur cet intervalle.

Détermination de la possibilité d'atteindre le maximum (minimum)
Une fonction atteint son maximum (minimum) sur l'ensemble s'il existe un argument pour lequel
pour tous .

Détermination de l'accessibilité de la face supérieure (inférieure)
Une fonction atteint sa limite supérieure (inférieure) sur l'ensemble s'il existe un argument pour lequel
.

Deuxième théorème de Weierstrass sur le maximum et le minimum d'une fonction continue
Une fonction continue sur un segment atteint sur celui-ci ses bornes supérieure et inférieure ou, ce qui revient au même, atteint son maximum et son minimum sur le segment.

Théorème des valeurs intermédiaires de Bolzano-Cauchy
Soit la fonction continue sur le segment. Et soit C un nombre arbitraire situé entre les valeurs de la fonction aux extrémités du segment : et . Il y a alors un point pour lequel
.

Corollaire 1
Soit la fonction continue sur le segment. Et laissez les valeurs de fonction aux extrémités du segment avoir des signes différents : ou . Il y a alors un point auquel la valeur de la fonction est égale à zéro :
.

Corollaire 2
Soit la fonction continue sur le segment. Laisse tomber . Ensuite la fonction prend sur l'intervalle toutes les valeurs de et uniquement ces valeurs :
à .

Fonctions inverses

Définition d'une fonction inverse
Soit une fonction avoir un domaine de définition X et un ensemble de valeurs Y. Et laissez-lui la propriété :
pour tous .
Alors pour tout élément de l’ensemble Y on ne peut associer qu’un seul élément de l’ensemble X auquel . Cette correspondance définit une fonction appelée fonction inverseÀ . La fonction inverse est notée comme suit :
.

De la définition il résulte que
;
pour tous ;
pour tous .

Lemme sur la monotonie mutuelle des fonctions directes et inverses
Si une fonction est strictement croissante (décroissante), alors il existe une fonction inverse qui est également strictement croissante (décroissante).

Propriété de symétrie des graphiques de fonctions directes et inverses
Les graphiques des fonctions directes et inverses sont symétriques par rapport à la droite.

Théorème sur l'existence et la continuité d'une fonction inverse sur un intervalle
Soit la fonction continue et strictement croissante (décroissante) sur le segment. Ensuite, la fonction inverse est définie et continue sur le segment, qui augmente (diminue) strictement.

Pour une fonction croissante. Pour diminuer - .

Théorème sur l'existence et la continuité d'une fonction inverse sur un intervalle
Soit la fonction continue et strictement croissante (décroissante) sur un intervalle ouvert fini ou infini. Ensuite, la fonction inverse est définie et continue sur l'intervalle, qui augmente (diminue) strictement.

Pour une fonction croissante.
Pour diminuer : .

De la même manière, on peut formuler le théorème sur l'existence et la continuité de la fonction inverse sur un demi-intervalle.

Propriétés et continuité des fonctions élémentaires

Les fonctions élémentaires et leurs inverses sont continues dans leur domaine de définition. Ci-dessous, nous présentons les formulations des théorèmes correspondants et fournissons des liens vers leurs preuves.

Fonction exponentielle

Fonction exponentielle f (x) = un x, avec base un > 0 est la limite de la séquence
,
où est une séquence arbitraire de nombres rationnels tendant vers x :
.

Théorème. Propriétés de la fonction exponentielle
La fonction exponentielle a les propriétés suivantes :
(P.0) défini, pour , pour tous ;
(P.1) pour un ≠ 1 a de nombreuses significations ;
(P.2) augmente strictement à , diminue strictement à , est constant à ;
(P.3) ;
(P.3*) ;
(P.4) ;
(P.5) ;
(P.6) ;
(P.7) ;
(P.8) continu pour tous;
(P.9)à ;
à .

Logarithme

Fonction logarithmique, ou logarithme, y = bûche, avec base un est l'inverse de la fonction exponentielle de base a.

Théorème. Propriétés du logarithme
Fonction logarithmique de base a, y = enregistrer un x, possède les propriétés suivantes :
(L.1) défini et continu, pour et , pour les valeurs positives de l'argument ;
(L.2) a de nombreuses significations ;
(L.3) augmente strictement comme , diminue strictement comme ;
(L.4)à ;
à ;
(L.5) ;
(L.6)à ;
(L.7)à ;
(L.8)à ;
(L.9)à .

Exposant et logarithme népérien

Dans les définitions de la fonction exponentielle et du logarithme, une constante apparaît, appelée base de la puissance ou base du logarithme. En analyse mathématique, dans la grande majorité des cas, des calculs plus simples sont obtenus si le nombre e est utilisé comme base :
.
Une fonction exponentielle de base e est appelée un exposant : , et un logarithme de base e est appelé un logarithme népérien : .

Les propriétés de l'exposant et du logarithme népérien sont présentées sur les pages
"Exposant, e à la puissance x",
"Logarithme népérien, fonction ln x"

Fonction de puissance

Fonction puissance avec exposant p est la fonction f (x) = xp, dont la valeur au point x est égale à la valeur de la fonction exponentielle de base x au point p.
De plus, f (0) = 0 p = 0 pour p > 0 .

Ici, nous considérerons les propriétés de la fonction puissance y = x p pour des valeurs non négatives de l'argument. Pour m rationnel, pour m impair, la fonction puissance est également définie pour x négatif. Dans ce cas, ses propriétés peuvent être obtenues en utilisant des valeurs paires ou impaires.
Ces cas sont discutés en détail et illustrés sur la page « Fonction puissance, ses propriétés et graphiques ».

Théorème. Propriétés de la fonction puissance (x ≥ 0)
Une fonction puissance, y = x p, d'exposant p a les propriétés suivantes :
(C.1) défini et continu sur le plateau
à ,
à ".

Fonctions trigonométriques

Théorème sur la continuité des fonctions trigonométriques
Fonctions trigonométriques : sinus ( péché x), cosinus ( parce que x), tangente ( tgx) et cotangente ( ctg x

Théorème sur la continuité des fonctions trigonométriques inverses
Fonctions trigonométriques inverses : arc sinus ( arcsin x), arc cosinus ( arccos x), arctangente ( arctan x) et l'arc tangent ( arcctg x), sont continus dans leurs domaines de définition.

Les références:
O.I. Bessov. Cours sur l'analyse mathématique. Partie 1. Moscou, 2004.
L.D. Kudryavtsev. Cours d'analyse mathématique. Tome 1. Moscou, 2003.
CM. Nikolski. Cours d'analyse mathématique. Tome 1. Moscou, 1983.

Continuité de fonction. Points de rupture.

Le taureau marche, se balance, soupire en marchant :
- Oh, la planche s'épuise, maintenant je vais tomber !

Dans cette leçon, nous examinerons le concept de continuité d'une fonction, la classification des points de discontinuité et un problème pratique courant études de continuité des fonctions. D'après le nom même du sujet, beaucoup devinent intuitivement ce qui sera discuté et pensent que le matériel est assez simple. C'est vrai. Mais ce sont les tâches simples qui sont le plus souvent punies pour négligence et approche superficielle de leur résolution. Par conséquent, je vous recommande d'étudier l'article très attentivement et d'en saisir toutes les subtilités et techniques.

Que faut-il savoir et pouvoir faire ? Pas beaucoup. Pour bien apprendre la leçon, il faut comprendre de quoi il s'agit limite d'une fonction. Pour les lecteurs ayant un faible niveau de préparation, il suffit de comprendre l'article Limites de fonction. Exemples de solutions et regardez la signification géométrique de la limite dans le manuel Graphiques et propriétés des fonctions élémentaires. Il est également conseillé de se familiariser avec transformations géométriques de graphiques, puisque la pratique consiste dans la plupart des cas à construire un dessin. Les perspectives sont optimistes pour tout le monde, et même une bouilloire pleine sera capable de faire face seule à la tâche dans une heure ou deux !

Continuité de fonction. Points d'arrêt et leur classification

Notion de continuité de fonction

Considérons une fonction continue sur toute la droite numérique :

Ou, pour le dire plus succinctement, notre fonction est continue sur (l'ensemble des nombres réels).

Quel est le critère « philistin » de continuité ? Évidemment, le graphique d’une fonction continue peut être tracé sans retirer le crayon du papier.

Dans ce cas, deux notions simples doivent être clairement distinguées : domaine d'une fonction Et continuité de fonction. En général ce n'est pas la même chose. Par exemple:

Cette fonction est définie sur toute la droite numérique, c'est-à-dire pour tout le monde La signification de « x » a sa propre signification de « y ». En particulier, si , alors . A noter que l'autre point est ponctué, car par la définition d'une fonction, la valeur de l'argument doit correspondre à la seule chose valeur de la fonction. Ainsi, domaine notre fonction : .

Cependant cette fonction n'est pas activée en continu ! Il est bien évident qu'au moment où elle souffre écart. Le terme est également tout à fait intelligible et visuel ; en effet, ici, il faudra de toute façon arracher le crayon du papier. Un peu plus tard, nous examinerons la classification des points d'arrêt.

Continuité d'une fonction en un point et sur un intervalle

Dans un problème mathématique particulier, on peut parler de continuité d'une fonction en un point, de continuité d'une fonction sur un intervalle, un demi-intervalle, ou encore de continuité d'une fonction sur un segment. C'est, il n’y a pas de « simple continuité »– la fonction peut être continue QUELQUE PART. Et la « pierre angulaire » fondamentale de tout le reste est continuité de fonction à ce point .

La théorie de l'analyse mathématique donne une définition de la continuité d'une fonction en un point en utilisant les voisinages « delta » et « epsilon », mais en pratique il existe une définition différente en usage, à laquelle nous porterons une attention particulière.

Rappelons-nous d'abord limites unilatérales qui a fait irruption dans nos vies dès la première leçon à propos des graphiques de fonctions. Considérons une situation quotidienne :

Si l'on s'approche de l'axe jusqu'au point gauche(flèche rouge), puis les valeurs correspondantes des « jeux » iront le long de l'axe jusqu'au point (flèche cramoisie). Mathématiquement, ce fait est corrigé en utilisant limite à gauche:

Faites attention à l'entrée (lit "x tend vers ka à gauche"). L'« additif » « moins zéro » symbolise , cela signifie essentiellement que nous approchons du nombre du côté gauche.

De même, si vous approchez du point « ka » sur la droite(flèche bleue), alors les « jeux » auront la même valeur, mais le long de la flèche verte, et limite à droite sera formaté comme suit :

"Additif" symbolise , et l'entrée se lit comme suit : "x tend vers ka à droite."

Si les limites unilatérales sont finies et égales(comme dans notre cas) : , alors nous dirons qu'il existe une limite GÉNÉRALE. C'est simple, la limite générale est notre « habituelle » limite d'une fonction, égal à un nombre fini.

Notez que si la fonction n'est pas définie en (faites ressortir le point noir sur la branche du graphique), alors les calculs ci-dessus restent valables. Comme cela a déjà été souligné à plusieurs reprises, notamment dans l'article sur les fonctions infinitésimales, les expressions signifient que "x" infiniment proche aborde le sujet, tandis que N'IMPORTE PAS, que la fonction elle-même soit définie à un moment donné ou non. Un bon exemple sera trouvé dans le paragraphe suivant, lorsque la fonction sera analysée.

Définition: une fonction est continue en un point si la limite de la fonction en un point donné est égale à la valeur de la fonction en ce point : .

La définition est détaillée dans les termes suivants :

1) La fonction doit être définie au point, c'est-à-dire que la valeur doit exister.

2) Il doit y avoir une limite générale de la fonction. Comme indiqué ci-dessus, cela implique l'existence et l'égalité de limites unilatérales : .

3) La limite de la fonction en un point donné doit être égale à la valeur de la fonction en ce point : .

En cas de violation au moins un des trois conditions, alors la fonction perd la propriété de continuité au point .

Continuité d'une fonction sur un intervalle est formulée ingénieusement et très simplement : une fonction est continue sur l'intervalle si elle est continue en tout point de l'intervalle donné.

En particulier, de nombreuses fonctions sont continues sur un intervalle infini, c'est-à-dire sur l'ensemble des nombres réels. Il s'agit d'une fonction linéaire, polynômes, exponentielle, sinus, cosinus, etc. Et en général, tout fonction élémentaire continu sur son domaine de définition, par exemple, une fonction logarithmique est continue sur l'intervalle . J'espère que vous avez maintenant une assez bonne idée de ce à quoi ressemblent les graphiques des fonctions de base. Des informations plus détaillées sur leur continuité peuvent être obtenues auprès d'un homme aimable nommé Fichtenholtz.

Avec la continuité d'une fonction sur un segment et des demi-intervalles, tout n'est pas non plus difficile, mais il est plus approprié d'en parler en classe sur la recherche des valeurs minimales et maximales d'une fonction sur un segment, mais pour l’instant ne nous en inquiétons pas.

Classement des points de rupture

La vie passionnante des fonctions est riche de toutes sortes de particularités, et les points d'arrêt ne sont qu'une des pages de leur biographie.

Note : au cas où, je m'attarderai sur un point élémentaire : le point de rupture est toujours point unique– il n’y a pas de « plusieurs points de rupture d’affilée », c’est-à-dire qu’il n’existe pas d’« intervalle de pause ».

Ces points, à leur tour, sont divisés en deux grands groupes : ruptures du premier type Et ruptures du deuxième type. Chaque type d'écart a ses propres caractéristiques, que nous allons examiner tout de suite :

Point de discontinuité du premier type

Si la condition de continuité est violée en un point et limites unilatérales fini , alors on l'appelle point de discontinuité du premier type.

Commençons par le cas le plus optimiste. Selon l'idée originale de la leçon, je voulais raconter la théorie « en termes généraux », mais afin de démontrer la réalité de la matière, j'ai opté pour l'option avec des personnages spécifiques.

C'est triste, comme une photo de jeunes mariés sur fond de Flamme éternelle, mais le plan suivant est généralement accepté. Représentons le graphique de la fonction dans le dessin :


Cette fonction est continue sur toute la droite numérique, à l’exception du point. Et en fait, le dénominateur ne peut pas être égal à zéro. Cependant, conformément au sens de la limite, on peut infiniment proche approchez-vous de « zéro » à la fois par la gauche et par la droite, c'est-à-dire que des limites unilatérales existent et coïncident évidemment :
(La condition n°2 de continuité est satisfaite).

Mais la fonction n'est pas définie à ce point, par conséquent, la condition n° 1 de continuité est violée et la fonction souffre d'une discontinuité à ce point.

Une rupture de ce type (avec l'existant limite générale) sont appelés espace réparable. Pourquoi amovible ? Parce que la fonction peut redéfinir au point de rupture :

Est-ce que ça a l'air bizarre ? Peut être. Mais une telle notation de fonction ne contredit rien ! Maintenant, l'écart est comblé et tout le monde est content :


Effectuons un contrôle formel :

2) – il existe une limite générale ;
3)

Ainsi, les trois conditions sont satisfaites et la fonction est continue en un point par la définition de continuité d'une fonction en un point.

Cependant, les détracteurs du matan peuvent mal définir la fonction, par exemple :


Il est intéressant de noter que les deux premières conditions de continuité sont ici satisfaites :
1) – la fonction est définie en un point donné ;
2) – il existe une limite générale.

Mais la troisième frontière n'a pas été franchie : , c'est-à-dire la limite de la fonction au point inégal la valeur d'une fonction donnée en un point donné.

Ainsi, à un moment donné, la fonction subit une discontinuité.

Le deuxième cas, plus triste, s'appelle rupture du premier type avec un saut. Et la tristesse est évoquée par des limites unilatérales qui fini et différent. Un exemple est montré dans le deuxième dessin de la leçon. Un tel écart se produit généralement dans fonctions définies par morceaux, qui ont déjà été mentionnés dans l'article à propos des transformations graphiques.

Considérons la fonction par morceaux et nous terminerons son dessin. Comment construire un graphique ? Très simple. Sur un demi-intervalle, nous dessinons un fragment de parabole (vert), sur un intervalle - un segment de droite (rouge) et sur un demi-intervalle - une ligne droite (bleue).

De plus, en raison de l'inégalité, la valeur est déterminée pour la fonction quadratique (point vert), et en raison de l'inégalité, la valeur est déterminée pour la fonction linéaire (point bleu) :

Dans le cas le plus difficile, il faudra recourir à une construction point par point de chaque élément du graphique (voir le premier leçon sur les graphiques de fonctions).

Maintenant, nous ne nous intéresserons qu'au point. Examinons-le pour la continuité :

2) Calculons les limites unilatérales.

Sur la gauche, nous avons un segment de ligne rouge, donc la limite du côté gauche est :

A droite se trouve la droite bleue, et la limite de droite :

En conséquence, nous avons reçu nombres finis, et ils inégal. Depuis les limites unilatérales fini et différent: , alors notre fonction tolère discontinuité du premier type avec saut.

Il est logique que l'écart ne puisse pas être éliminé - la fonction ne peut vraiment pas être définie davantage et « collée ensemble », comme dans l'exemple précédent.

Points de discontinuité du deuxième type

Habituellement, tous les autres cas de rupture sont judicieusement classés dans cette catégorie. Je ne vais pas tout énumérer, car en pratique, dans 99% des problèmes que vous rencontrerez écart sans fin– qu’on soit gaucher ou droitier, et le plus souvent, les deux limites sont infinies.

Et bien sûr, l’image la plus évidente est l’hyperbole au point zéro. Ici, les deux limites unilatérales sont infinies : , la fonction subit donc une discontinuité du deuxième type au point .

J'essaie de remplir mes articles avec un contenu le plus diversifié possible, regardons donc le graphique d'une fonction qui n'a pas encore été rencontrée :

selon le schéma standard :

1) La fonction n'est pas définie à ce stade car le dénominateur tend vers zéro.

Bien sûr, on peut immédiatement conclure que la fonction subit une discontinuité au point , mais il serait bon de classifier la nature de la discontinuité, ce qui est souvent requis par la condition. Pour ça:

Permettez-moi de vous rappeler que par enregistrement, nous entendons nombre négatif infinitésimal, et sous l'entrée - nombre positif infinitésimal.

Les limites unilatérales sont infinies, ce qui signifie que la fonction subit une discontinuité de 2ème espèce au point . L'axe y est asymptote verticale pour le graphique.

Il n'est pas rare que les deux limites unilatérales existent, mais une seule d'entre elles est infinie, par exemple :

C'est le graphique de la fonction.

Nous examinons le point de continuité :

1) La fonction n'est pas définie à ce stade.

2) Calculons les limites unilatérales :

Nous parlerons de la méthode de calcul de ces limites unilatérales dans les deux derniers exemples de la conférence, bien que de nombreux lecteurs aient déjà tout vu et deviné.

La limite de gauche est finie et égale à zéro (on « ne va pas au point lui-même »), mais la limite de droite est infinie et la branche orange du graphe se rapproche de l'infini de sa asymptote verticale, donné par l'équation (ligne pointillée noire).

La fonction en souffre donc discontinuité de deuxième type au point .

Comme pour une discontinuité de 1ère espèce, la fonction peut être définie au point de discontinuité lui-même. Par exemple, pour une fonction par morceaux N'hésitez pas à mettre un point noir gras à l'origine des coordonnées. A droite se trouve une branche d'une hyperbole et la limite de droite est infinie. Je pense que presque tout le monde a une idée de ce à quoi ressemble ce graphique.

Ce que tout le monde attendait avec impatience :

Comment examiner la continuité d’une fonction ?

L'étude d'une fonction de continuité en un point s'effectue selon un schéma de routine déjà établi, qui consiste à vérifier trois conditions de continuité :

Exemple 1

Fonction Explorer

Solution:

1) Le seul point dans le champ d'application est celui où la fonction n'est pas définie.

2) Calculons les limites unilatérales :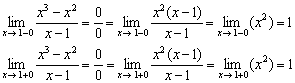

Les limites unilatérales sont finies et égales.

Ainsi, à ce moment-là, la fonction souffre d'une discontinuité amovible.

A quoi ressemble le graphique de cette fonction ?

je voudrais simplifier , et il semble qu'une parabole ordinaire soit obtenue. MAIS la fonction d'origine n'est pas définie au point , donc la clause suivante est requise :

Faisons le dessin :

Répondre: la fonction est continue sur toute la droite numérique sauf le point où elle subit une discontinuité amovible.

La fonction peut être définie plus en détail d'une manière bonne ou moins bonne, mais selon la condition, cela n'est pas requis.

Vous dites que c'est un exemple tiré par les cheveux ? Pas du tout. Cela s'est produit des dizaines de fois dans la pratique. La quasi-totalité des tâches du site proviennent de véritables travaux et tests indépendants.

Débarrassons-nous de nos modules préférés :

Exemple 2

Fonction Explorer pour la continuité. Déterminer la nature des discontinuités de fonction, si elles existent. Exécutez le dessin.

Solution: Pour une raison quelconque, les étudiants ont peur et n'aiment pas les fonctions avec un module, même si elles n'ont rien de compliqué. Nous avons déjà abordé un peu ces choses dans la leçon. Transformations géométriques des graphiques. Le module étant non négatif, il est développé comme suit : , où « alpha » est une expression. Dans ce cas, notre fonction doit être écrite par morceaux :

Mais les fractions des deux morceaux doivent être réduites de . La réduction, comme dans l’exemple précédent, ne se fera pas sans conséquences. La fonction d'origine n'est pas définie au point puisque le dénominateur tend vers zéro. Par conséquent, le système doit en outre spécifier la condition et rendre la première inégalité stricte :

Parlons maintenant d'une technique de décision TRÈS UTILE: avant de finaliser la tâche sur un brouillon, il est avantageux de faire un dessin (peu importe si les conditions l'exigent ou non). Cela aidera, d'une part, à voir immédiatement les points de continuité et les points de discontinuité, et, d'autre part, cela vous protégera à 100 % des erreurs lors de la recherche de limites unilatérales.

Faisons le dessin. Conformément à nos calculs, à gauche du point il faut dessiner un fragment de parabole (couleur bleue), et à droite - un morceau de parabole (couleur rouge), alors que la fonction n'est pas définie au point lui-même :

En cas de doute, prenez quelques valeurs x et branchez-les dans la fonction (en vous rappelant que le module détruit l'éventuel signe moins) et vérifiez le graphique.

Examinons analytiquement la fonction de continuité :

1) La fonction n'est pas définie au point, on peut donc immédiatement dire qu'elle n'y est pas continue.

2) Établissons la nature de la discontinuité ; pour ce faire, nous calculons des limites unilatérales :

Les limites unilatérales sont finies et différentes, ce qui fait que la fonction subit une discontinuité de 1ère espèce avec un saut au point . Notez encore une fois que lors de la recherche de limites, peu importe que la fonction au point d'arrêt soit définie ou non.

Il ne reste plus qu'à transférer le dessin du brouillon (il a été réalisé comme avec l'aide de la recherche ;-)) et à terminer la tâche :

Répondre: la fonction est continue sur toute la droite numérique sauf au point où elle subit une discontinuité de première espèce avec un saut.

Parfois, ils nécessitent une indication supplémentaire du saut de discontinuité. Il est calculé simplement - de la limite droite, vous devez soustraire la limite gauche : , c'est-à-dire qu'au point d'arrêt, notre fonction a sauté de 2 unités (comme nous l'indique le signe moins).

Exemple 3

Fonction Explorer pour la continuité. Déterminer la nature des discontinuités de fonction, si elles existent. Faites un dessin.

Ceci est un exemple à résoudre par vous-même, un exemple de solution à la fin de la leçon.

Passons à la version la plus populaire et la plus répandue de la tâche, lorsque la fonction se compose de trois parties :

Exemple 4

Examiner la continuité d'une fonction et tracer un graphique de la fonction .

Solution: il est évident que les trois parties de la fonction sont continues sur les intervalles correspondants, il ne reste donc plus qu'à vérifier deux points de « jonction » entre les pièces. Commençons par faire un brouillon de dessin, j'ai commenté la technique de construction de manière suffisamment détaillée dans la première partie de l'article. La seule chose est qu'il faut suivre attentivement nos points singuliers : en raison de l'inégalité, la valeur appartient à la droite (point vert), et en raison de l'inégalité, la valeur appartient à la parabole (point rouge) :


Bon, en principe, tout est clair =) Il ne reste plus qu'à formaliser la décision. Pour chacun des deux points « de jonction », on vérifie classiquement 3 conditions de continuité :

JE) Nous examinons le point de continuité

1)

Les limites unilatérales sont finies et différentes, ce qui fait que la fonction subit une discontinuité de 1ère espèce avec un saut au point .

Calculons le saut de discontinuité comme la différence entre les limites droite et gauche :
, c'est-à-dire que le graphique a augmenté d'une unité.

II) Nous examinons le point de continuité

1) – la fonction est définie en un point donné.

2) Trouvez des limites unilatérales :

– les limites unilatérales sont finies et égales, ce qui signifie qu’il existe une limite générale.

3) – la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Au stade final, nous transférons le dessin vers la version finale, après quoi nous mettons l'accord final :

Répondre: la fonction est continue sur toute la droite numérique, à l'exception du point où elle subit une discontinuité de première espèce avec un saut.

Exemple 5

Examiner une fonction pour la continuité et construire son graphique .

Ceci est un exemple de solution indépendante, une solution courte et un échantillon approximatif du problème à la fin de la leçon.

On peut avoir l’impression qu’à un moment donné la fonction doit être continue et à un autre il doit y avoir une discontinuité. En pratique, ce n’est pas toujours le cas. Essayez de ne pas négliger les exemples restants - il y aura plusieurs fonctionnalités intéressantes et importantes :

Exemple 6

Étant donné une fonction . Étudiez la fonction pour la continuité à certains points. Construisez un graphique.

Solution: et encore une fois, exécutez immédiatement le dessin sur le brouillon :

La particularité de ce graphique est que la fonction par morceaux est donnée par l'équation de l'axe des abscisses. Ici cette zone est dessinée en vert, mais dans un cahier elle est généralement soulignée en gras avec un simple crayon. Et bien sûr, n’oubliez pas nos béliers : la valeur appartient à la branche tangente (point rouge), et la valeur appartient à la droite.

Tout est clair sur le dessin - la fonction est continue sur toute la droite numérique, il ne reste plus qu'à formaliser la solution, qui est amenée à une automatisation complète littéralement après 3-4 exemples similaires :

JE) Nous examinons le point de continuité

1) – la fonction est définie en un point donné.

2) Calculons les limites unilatérales :

, ce qui signifie qu'il existe une limite générale.

Au cas où, permettez-moi de vous rappeler un fait trivial : la limite d'une constante est égale à la constante elle-même. Dans ce cas, la limite de zéro est égale à zéro lui-même (limite à gauche).

3) – la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Ainsi, une fonction est continue en un point par la définition de continuité d'une fonction en un point.

II) Nous examinons le point de continuité

1) – la fonction est définie en un point donné.

2) Trouvez des limites unilatérales :

Et ici – la limite d’un est égale à l’unité elle-même.

– il existe une limite générale.

3) – la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Ainsi, une fonction est continue en un point par la définition de continuité d'une fonction en un point.

Comme d'habitude, après recherche nous transférons notre dessin vers la version finale.

Répondre: la fonction est continue aux points.

Veuillez noter que dans la condition on ne nous a rien demandé sur l'étude de la continuité de la fonction entière, et il est considéré comme une bonne forme mathématique de formuler précis et clair la réponse à la question posée. À propos, si les conditions ne vous obligent pas à construire un graphique, vous avez parfaitement le droit de ne pas le construire (bien que plus tard, l'enseignant puisse vous forcer à le faire).

Un petit « virelangue » mathématique pour le résoudre vous-même :

Exemple 7

Étant donné une fonction . Étudiez la fonction pour la continuité à certains points. Classez les points d’arrêt, le cas échéant. Exécutez le dessin.

Essayez de "prononcer" tous les "mots" correctement =) Et dessinez le graphique plus précisément, avec précision, ce ne sera pas superflu partout ;-)

Comme vous vous en souvenez, j'ai recommandé de terminer immédiatement le dessin sous forme de brouillon, mais de temps en temps, vous rencontrez des exemples où vous ne pouvez pas comprendre immédiatement à quoi ressemble le graphique. Par conséquent, dans certains cas, il est avantageux de trouver d’abord les limites unilatérales et ensuite seulement, sur la base de l’étude, de représenter les branches. Dans les deux derniers exemples, nous apprendrons également une technique pour calculer certaines limites unilatérales :

Exemple 8

Examinez la continuité de la fonction et construisez son graphique schématique.

Solution: les mauvais points sont évidents : (réduit le dénominateur de l'exposant à zéro) et (réduit le dénominateur de la fraction entière à zéro). On ne sait pas exactement à quoi ressemble le graphique de cette fonction, ce qui signifie qu'il est préférable de faire d'abord quelques recherches.