Les séries Laurent isolent les points singuliers et leur classification. Point singulier

Les séries de Taylor constituent un outil efficace pour étudier les fonctions analytiques dans un cercle. Pour étudier les fonctions analytiques dans un domaine en anneau, il s'avère possible de construire des développements en puissances positives et négatives (z - zq) de la forme qui généralisent les développements de Taylor. La série (1), comprise comme la somme de deux séries, est appelée série de Laurent. Il est clair que la région de convergence de la série (1) est la partie commune des régions de convergence de chacune des séries (2). Trouvons-la. L'aire de convergence de la première série est un cercle dont le rayon est déterminé par la formule de Cauchy-Hadamard. A l'intérieur du cercle de convergence, la série (3) converge vers une fonction analytique, et dans tout cercle de rayon plus petit, elle converge absolument et uniformément. La deuxième rangée est série de puissance par rapport à une variable, la série (5) converge à l'intérieur de son cercle de convergence vers une fonction analytique d'une variable complexe m-*oo, et dans tout cercle de rayon plus petit elle converge de manière absolue et uniforme, ce qui signifie que l'aire de convergence de la série (4) est l'extérieur du cercle - Si alors existe l'aire commune de convergence des séries (3) et (4) est un anneau circulaire dans lequel la série (1) converge vers une fonction analytique. De plus, dans n'importe quel anneau, il converge de manière absolue et uniforme. Exemple 1. Déterminer la région de convergence des séries de Rad Laurent Points singuliers isolés et leur classification M La région de convergence de la première série est l'extérieur du cercle et la région de convergence de la deuxième série est l'intérieur du cercle Ainsi, cette série converge en cercles Théorème 15. Toute fonction f (z), univoque et apolitique dans un anneau circulaire peut être représentée dans cet anneau comme la somme d'une série convergente dont les coefficients Cn sont déterminés de manière unique et calculés selon les formules où 7p est un cercle de rayon m. Fixons un point arbitraire z à l'intérieur de l'anneau R. Construisons des cercles de centre au point r, dont les rayons satisfont aux inégalités et considérons un nouvel anneau. En utilisant le théorème intégral de Cauchy pour un domaine multiconnecté, nous avons Nous transformons séparément chacune des intégrales dans la somme (8). Pour tous les points £ le long du cercle 7d* la relation de somme de la série uniformément convergente 1 1 est satisfaite. Par conséquent, la fraction ^ peut être représentée dans vi- / "/ En multipliant les deux parties par une fonction continue (O et en effectuant En intégrant terme par terme le long du cercle, nous obtenons que nous effectuons la transformation de la seconde intégrale de manière quelque peu différente. Pour tous les points £ du cercle ir>, la relation est vraie. Par conséquent, la fraction ^ peut être représentée comme la somme de une série uniformément convergente. En multipliant les deux côtés par une fonction continue) et en intégrant par terme le long du cercle 7/, on obtient que Notez que les intégrandes dans les formules (10) et (12) sont des fonctions analytiques dans un anneau circulaire. Par conséquent, d'après la formule de Cauchy théorème, les valeurs des intégrales correspondantes ne changeront pas si l'on remplace les cercles 7/r et 7r/ par n'importe quel cercle. Cela nous permet de combiner les formules (10) et (12) , Remplacement des intégrales du côté droit de formule (8) avec leurs expressions (9) et (11), respectivement, on obtient le développement requis. Puisque z est un point arbitraire de l'anneau, il s'ensuit que la série (14) converge vers la fonction f(z) partout dans cet anneau, et dans tout anneau, la série converge absolument et uniformément vers cette fonction. Montrons maintenant que la décomposition de la forme (6) est unique. Supposons qu'il y ait encore une expansion, alors partout à l'intérieur de l'anneau R nous aurons Sur le cercle, les séries (15) convergent uniformément. Multiplions les deux côtés de l'égalité (où m est un entier fixe, et intégrons les deux séries terme par terme. En conséquence, nous obtenons à gauche et à droite - Sch. Ainsi, (4, = St. Puisque m est un nombre arbitraire, la dernière égalité prouve le caractère unique du développement. La série (6), dont les coefficients sont calculés à l'aide des formules (7), est appelée série de Laurent de la fonction f(z) dans l'anneau. ensemble de termes de cette série sans pouvoirs négatifs appelé la bonne partie Série Laurent, et avec les négatifs - sa partie principale. Les formules (7) pour les coefficients de la série Laurent sont rarement utilisées dans la pratique car, en règle générale, elles nécessitent des calculs fastidieux. Habituellement, si possible, des développements de Taylor prêts à l'emploi de fonctions élémentaires sont utilisés. Compte tenu du caractère unique de la décomposition, toute méthode juridique conduit au même résultat. Exemple 2. Considérons les développements de fonctions en série Laurent dans divers domaines, en supposant que Fuiscia /(r) a deux points singuliers : . Par conséquent, il existe trois régions annulaires, dont le centre est le point r = 0. Dans chacune d'elles, la fonction f(r) est analytique : a) un cercle est un anneau, l'extérieur d'un cercle (Fig. 27). Trouvons les développements de Laurent de la fonction /(z) dans chacune de ces régions. Représentons /(z) comme une somme de fractions élémentaires a) Cercle On transforme la relation (16) comme suit : En utilisant la formule de la somme des termes progression géométrique, on obtient Remplacer les développements trouvés par la formule (17) : Ce développement est la série de Taylor de la fonction /(z). b) L'anneau de la fonction -r reste convergent dans cet anneau, puisque la série (19) pour la fonction j^j pour |z| > 1 diverge. Par conséquent, nous transformons la fonction /(z) comme suit : en appliquant à nouveau la formule (19), nous obtenons que Cette série converge pour. En substituant les développements (18) et (21) dans la relation (20), nous obtenons c) L'extérieur du cercle pour la fonction -z pour |z| > 2 divergents, et série (21) pour la fonction Représentons la fonction /(z) sous la forme suivante : /<*>En utilisant les formules (18) et (19), on obtient OR 1 Cet exemple montre que pour la même fonction f(z) le développement de Laurent, d'une manière générale, a différentes sortes pour différentes bagues. Exemple 3. Trouver le développement de la 8ème série de Laurent d'une fonction Série de Laurent Points singuliers isolés et leur classification dans un domaine en anneau A On utilise la représentation de la fonction f(z) sous la forme suivante : et transformer le deuxième terme En utilisant le formule pour la somme des termes d'une progression géométrique, nous obtenons En remplaçant les expressions trouvées dans la formule (22), nous avons l'exemple 4. Développez la fonction dans la série de Laurent dans la région zq = 0. Pour tout complexe, nous avons Soit ceci l'expansion est valable pour tout point z Ф 0. Dans ce cas, la région annulaire représente l'ensemble du plan complexe avec un point z - 0 ignoré. Cette région peut être définie par la relation suivante : Cette fonction est analytique dans la région Des formules ( 13) pour les coefficients de la série de Laurent, en utilisant le même raisonnement que dans le paragraphe précédent, on peut obtenir les inégalités de Kouiw. si la fonction f(z) est bornée sur un cercle, où M est une constante), alors Points singuliers isolés Le point zo est appelé point singulier isolé de la fonction f(z) s'il existe un voisinage annulaire du point ( cet ensemble est parfois appelé voisinage perforé du point 2o), pour lequel la fonction f(z) est unique et analytique. Au point zo lui-même, la fonction est soit indéfinie, soit non univoque et analytique. Selon le comportement de la fonction /(r) à l'approche du point zo, on distingue trois types de points singuliers. Un point singulier isolé est appelé : 1) amovible s'il existe un fini 2) pmusach si 3) un point essentiellement singulier si la fonction f(z) n'a pas de limite à Le type d'un point singulier isolé est étroitement lié au nature de l'expansion laurentienne de la fonction par le centre perforé de . Théorème 16. Un point singulier isolé z0 d'une fonction f(z) est un point singulier amovible si et seulement si le développement de Laurent de la fonction f(z) au voisinage du point zo ne contient pas de partie principale, c'est-à-dire a la forme Soit zo un point singulier amovible. Alors il y a un fini, donc la fonction f(z) est bornée dans un voisinage prologique du point z. Nous mettons En vertu des inégalités de Cauchy Puisque p peut être choisi arbitrairement petit, alors tous les coefficients à des puissances négatives (z - 20) sont égaux à zéro : Inversement, soit Laurent le développement de la fonction /(r) au voisinage du point zq ne contient que la partie correcte, c'est-à-dire qu'elle a la forme (23) et est donc Taylor. Il est facile de voir que pour z -* z0 la fonction /(z) a une valeur limite : Théorème 17. Un point singulier isolé zq de la fonction f(z) est amovible si et seulement si la fonction J(z) est délimité dans quelque quartier perforé du point zq, Zgmechai pas. Soit r un point singulier amovible de la fonction /(r). En supposant que nous obtenions que la fonction /(r) est analytique dans un cercle dont le centre est le point r. Cela détermine le nom du point - amovible. Théorème 18. Un point singulier isolé zq d'une fonction f(z) est un pôle si et seulement si la partie principale du développement de Laurent de la fonction f(z) au voisinage du point contient un nombre fini (et positif) de termes non nuls, c'est-à-dire a la forme 4. Soit z0 un pôle. Depuis il existe un voisinage perforé du point z0 dans lequel la fonction f(z) est analytique et non nulle. Alors dans ce voisinage une fonction analytique est définie et donc, le point zq est un point singulier amovible (zéro) de la fonction ou où h(z) est une fonction analytique, h(z0) Φ 0. Alors h(zo) Φ 0 est aussi analytique, alors la fonction φ est analytique dans un voisinage du point zq, et donc, d'où on obtient que Supposons maintenant que la fonction f(z) ait un développement de la forme (24) dans un voisinage perforé de le point zо. Cela signifie que dans ce voisinage la fonction f(z) est analytique avec la fonction. Pour la fonction g(z) le développement est valide, d'où on peut voir que zq est un point singulier amovible de la fonction g(z) et existe. Alors la fonction en 0 tend à être le pôle de la fonction. est un autre fait simple. Le point Zq est un pôle de la fonction f(z) si et seulement si la fonction g(z) = yj peut être étendue à une fonction analytique au voisinage du point zq en posant g(z0) = 0. L'ordre du pôle de la fonction f(z) est appelé ordre zéro de la fonction jfa. L’énoncé suivant découle des théorèmes 16 et 18. Théorème 19. Un point singulier isolé est essentiellement singulier si et seulement si la partie principale du développement de Laurent dans un voisinage perforé de ce point contient une infinité de termes non nuls. Exemple 5. Le point singulier de la fonction est zo = 0. Nous avons la série Laurent Points singuliers isolés et leur classification Par conséquent, zo = O est un point singulier amovible. Le développement de la fonction /(z) dans une série de Laurent au voisinage du point zéro ne contient que la partie correcte : Exemple7. /(z) = Le point singulier de la fonction f(z) est zq = 0. Considérons le comportement de cette fonction sur les axes réel et imaginaire : sur l'axe réel en x 0, sur l'axe imaginaire Par conséquent, il y a n'est ni une limite finie ni une limite infinie pour f(z) à z -* 0 n'existe pas. Cela signifie que le point r = 0 est un point essentiellement singulier de la fonction f(z). Trouvons le développement de Laurent de la fonction f(z) au voisinage du point zéro. Pour tout complexe C, nous avons Set. Alors le développement de Laurent contient un nombre infini de termes de puissances négatives de z.

Modèles décrits par des systèmes de deux équations différentielles autonomes.

Plan de phase. Portrait de phase. Méthode Isoclin. Principales isoclines. Durabilité état stable. Systèmes linéaires. Types de points singuliers : nœud, selle, foyer, centre. Exemple: réactions chimiques Premier ordre.

Les résultats les plus intéressants sur la modélisation qualitative des propriétés des systèmes biologiques ont été obtenus à l'aide de modèles de deux équations différentielles permettant recherche qualitative en utilisant la méthode plan de phase. Considérons un système de deux équations différentielles ordinaires autonomes vue générale

(4.1)

P(x,y), Q(x,y)- fonctions continues, défini dans une zone g Plan euclidien ( x,y ‑ Coordonnées cartésiennes) et ayant dans cette région des dérivées continues d'ordre non inférieur au premier.

Région g peut être illimité ou limité. Si les variables x, y ont une signification biologique spécifique (concentrations de substances, nombre d'espèces) le plus souvent la zone g représente le quadrant positif du demi-plan droit :

0 £ X< ¥ ,0 £ oui< ¥ .

Les concentrations de substances ou le nombre d'espèces peuvent également être limitées d'en haut par le volume du navire ou la superficie de l'habitat. Alors la plage de variables a la forme :

0 £ X< x 0 , 0 £ oui< y 0 .

Variables x, y changement dans le temps conformément au système d'équations (4.1), de sorte que chaque état du système corresponde à une paire de valeurs variables ( x, y).

A l’inverse, chaque paire de variables ( x, y) correspond à un certain état du système.

Considérons un plan avec des axes de coordonnées sur lequel sont tracées les valeurs des variables x,y. Chaque point M ce plan correspond à un certain état du système. Ce plan est appelé plan de phase et représente la totalité de tous les états du système. Le point M(x,y) est appelé point représentant ou représentant.

Laissez au moment initial du temps t = t 0 coordonnées du point représentant M 0 (X(t 0), oui(t 0)). À chaque instant suivant dans le temps t le point représentatif se déplacera en fonction des changements dans les valeurs des variables X(t), oui(t). Collecte de points M(X(t), yt)) sur le plan de phase dont la position correspond aux états du système en train de changer de variables dans le temps x(t), yt) d’après les équations (4.1), est appelé trajectoire des phases.

L'ensemble des trajectoires de phase pour différentes valeurs initiales des variables donne un « portrait » facilement visible du système. Construction portrait de phase vous permet de tirer des conclusions sur la nature des changements dans les variables x, y sans connaissance des solutions analytiques du système d'équations d'origine(4.1).

Pour représenter un portrait de phase, il est nécessaire de construire un champ vectoriel de directions des trajectoires du système en chaque point du plan de phase. Réglage de l'incrémentD t>0,nous obtenons les incréments correspondants D X Et D ouià partir d'expressions :

D x=P(x,y)D t,

D y=Q(x,y)D t.

Direction du vecteur jour/dx au point ( x, y) dépend du signe des fonctions P(x, y), Q(x, y) et peut être donné par un tableau :

.(4.2)

Solution à cette équation y = y(x,c), ou implicitement F(x,y)=c, Où Avec– constante d'intégration, donne la famille des courbes intégrales de l'équation (4.2) - trajectoires de phases système (4.1) dans l'avion x, y.

Méthode isocline

Pour construire un portrait de phase, ils utilisent méthode isocline – des lignes sont tracées sur le plan de phase qui coupent les courbes intégrales à un angle spécifique. L’équation de l’isocline peut être facilement obtenue à partir de (4.2). Mettons

Où UN– une certaine valeur constante. Signification UN représente la tangente de l'angle d'inclinaison de la tangente à la trajectoire de la phase et peut prendre les valeurs de –¥ à + ¥ . Remplacer à la place jour/dx en (4.2) la quantité UN on obtient l'équation de l'isocline :

.(4.3)

L'équation (4.3) définit en chaque point du plan une tangente unique à la courbe intégrale correspondante, à l'exception du point où P(x,y)= 0,Q (x,y) = 0 , dans lequel la direction de la tangente devient incertaine, puisque la valeur de la dérivée devient incertaine :

.

Ce point est le point d'intersection de toutes les isoclines - point particulier. Dans ce document, les dérivées temporelles des variables disparaissent simultanément X Et oui.

Ainsi, en un point singulier, les taux de changement des variables sont nuls. Par conséquent, le point singulier des équations différentielles des trajectoires de phase (4.2) correspond à état stationnaire du système(4.1), et ses coordonnées sont les valeurs stationnaires des variables x, y.

Sont particulièrement intéressants isoclines principales :

dy/dx=0, P(x,y)=0 – isocline des tangentes horizontales et

jour/dx=¥ ,Q(x,y)=0 – isocline des tangentes verticales.

En construisant les isoclines principales et en trouvant leur point d'intersection (x,y), dont les coordonnées satisfont aux conditions :

on trouvera ainsi le point d'intersection de toutes les isoclines du plan de phase, dans lequel la direction des tangentes aux trajectoires de phase est incertaine. Ce - point singulier, ce qui correspond état stationnaire du système(Fig. 4.2).

Le système (4.1) possède autant d’états stationnaires qu’il y a de points d’intersection des isoclines principales sur le plan de phase.

Chaque trajectoire de phase correspond à un ensemble de mouvements d'un système dynamique, passant par les mêmes états et ne différant les uns des autres qu'au début du décompte du temps.

Si les conditions du théorème de Cauchy sont satisfaites, alors à travers chaque point de l’espace x, y, t il n'y a qu'une seule courbe intégrale. Il en est de même, du fait de l'autonomie, pour les trajectoires de phase : une trajectoire monophasée passe par chaque point du plan de phase.

Stabilité à l’état stable

Laissez le système être dans un état d’équilibre.

Alors le point représentatif est situé en un des points singuliers du système, auquel, par définition :

.

La stabilité ou non d'un point singulier est déterminée par le fait que le point représentatif quitte ou non l'état stationnaire avec un léger écart. Par rapport à un système de deux équations, la définition de la stabilité dans le langagee, dcomme suit.

L'état d'équilibre est stable si, pour une plage donnée d'écarts par rapport à l'état d'équilibre (e )vous pouvez spécifier la zone d (e ), entourant l'état d'équilibre et ayant la propriété qu'aucune trajectoire ne commence à l'intérieur de la région d , n'atteindra jamais la frontière e . (Fig. 4.4)

Pour une grande classe de systèmes - systèmes bruts – dont la nature du comportement ne change pas avec un petit changement dans la forme des équations, des informations sur le type de comportement au voisinage d'un état stationnaire peuvent être obtenues en examinant non pas l'original, mais un modèle simplifié linéarisé système.

Systèmes linéaires.

Considérons un système de deux équations linéaires:

.(4.4)

Ici a B c d- des constantes, x, y- Coordonnées cartésiennes sur le plan de phase.

Nous chercherons une solution générale sous la forme :

.(4.5)

Remplaçons ces expressions dans (4.4) et réduisons de e je t:

(4.6)

Système algébrique d'équations (4.6) à inconnues UN B n'a de solution non nulle que si son déterminant, composé des coefficients des inconnues, est égal à zéro :

.

En développant ce déterminant, on obtient l'équation caractéristique du système :

.(4.7)

La résolution de cette équation donne les valeurs des exposantsje 1,2 , pour lequel des valeurs non nulles sont possibles pour UN Et B solutions à l’équation (4.6). Ces significations sont

.(4.8)

Si l’expression radicale est négative, alorsje 1,2 nombres conjugués complexes. Supposons que les deux racines de l’équation (4.7) ont des parties réelles non nulles et qu’il n’y a pas de racines multiples. Alors la solution générale du système (4.4) peut être représentée comme une combinaison linéaire d'exponentielles avec des exposantsje 1 , je 2 :

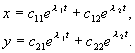(4.9)

Pour analyser la nature des trajectoires possibles du système sur le plan de phase, nous utilisons transformation de coordonnées homogènes linéaires, ce qui conduira le système à Forme canonique:

,(4.10)

permettant une représentation plus pratique sur le plan de phase par rapport au système original (4.4). Introduisons de nouvelles coordonnéesξ , η selon les formules :

(4.1)

Du cours d'algèbre linéaire, on sait que dans le cas d'inégalité mettre à zéro les parties réellesje 1 , je 2 le système original (4.4) peut toujours être transformé à l'aide de transformations (4.11) vers la forme canonique (4.10) et son comportement sur le plan des phases peut être étudiéξ , η . Considérons les différents cas qui peuvent se présenter ici.

Racines λ 1 , λ 2 – valide et du même signe

Dans ce cas les coefficients de transformation sont réels, on s'éloigne du plan réelx,yau plan réel ξ, η. En divisant la seconde des équations (4.10) par la première, on obtient:

.(4.12)

En intégrant cette équation, on trouve:

Où .(4.13)

Acceptons de comprendre par λ 2 la racine de l'équation caractéristique à grand module, ce qui ne viole pas la généralité de notre raisonnement. Alors, puisque dans le cas considéré les racines λ 1 , λ 2 – valide et de même signe,un>1 , et nous avons affaire à des courbes intégrales de type parabolique.

Toutes les courbes intégrales (sauf l'axe η , ce qui correspond à ) toucher à l'origine de l'axe ξ, qui est aussi la courbe intégrale de l’équation (4.11). L'origine des coordonnées est un point particulier.

Découvrons maintenant la direction de déplacement du point représentatif le long des trajectoires de phase. Si λ 1 , λ 2 sont donc négatifs, comme le montrent les équations (4.10), |ξ|, |η| diminuer avec le temps. Le point représentatif s'approche de l'origine des coordonnées, mais ne l'atteint jamais. Sinon, cela contredirait le théorème de Cauchy, qui stipule qu'une seule trajectoire de phase passe par chaque point du plan de phase.

Un point si particulier par lequel passent les courbes intégrales, tout comme une famille de paraboles passe par l’origine et est appelé nœud (Fig. 4.5)

État d'équilibre du type de nœud à λ 1 , λ 2 < 0 est Lyapunov stable, puisque le point représentatif se déplace le long de toutes les courbes intégrales vers l'origine des coordonnées. Ce nœud stable. Si λ 1 , λ 2 > 0, alors |ξ|, |η| augmentent avec le temps et le point représentatif s’éloigne de l’origine des coordonnées. Dans ce cas, le point particulier– nœud instable .

Sur le plan des phases x, y le caractère qualitatif général du comportement des courbes intégrales sera conservé, mais les tangentes aux courbes intégrales ne coïncideront pas avec les axes de coordonnées. L'angle d'inclinaison de ces tangentes sera déterminé par le rapport des coefficients α , β , γ , δ dans les équations (4.11).

Racines λ 1 , λ 2 – sont valables et de signes différents.

Convertir à partir de coordonnées x,y coordonner ξ, η encore une fois réel. Les équations pour les variables canoniques ont à nouveau la forme (4.10), mais maintenant les signes de λ 1 , λ 2 sont différents. L'équation des trajectoires de phase a la forme:

Où ,(4.14)

En intégrant (4.14), on trouve

(4.15)

Ce l'équation définit une famille de courbes de type hyperbolique, où les deux axes de coordonnées– asymptotes (à un=1 on aurait une famille d'hyperboles équilatérales). Les axes de coordonnées dans ce cas sont également des courbes intégrales– ce seront les seules courbes intégrales passant par l'origine. Chaquedont se compose de trajectoires en trois phases: de deux mouvements vers un état d'équilibre (ou depuis un état d'équilibre) et depuis un état d'équilibre. Toutes les autres courbes intégrales– sont des hyperboles qui ne passent pas par l'origine (Fig. 4.6) Ce point particulier est appelé "selle ». Les lignes de niveau près d'une selle de montagne se comportent de la même manière que les trajectoires de phase à proximité d'une selle.

Considérons la nature du mouvement du point représentatif le long de trajectoires de phase proches de l'état d'équilibre. Laissez, par exemple,λ 1 >0 , λ 2<0 . Puis le point représentant placé sur l'axe ξ , s'éloignera de l'origine, et se placera sur l'axe η – s'approchera indéfiniment de l'origine des coordonnées, sans l'atteindre dans un temps fini. Partout où se trouve le point représentatif au moment initial (à l'exception du point singulier et des points sur l'asymptote η =0), il finira par s'éloigner de l'état d'équilibre, même s'il se déplace initialement le long d'une des courbes intégrales vers le point singulier.

Il est évident que un point singulier comme une selle est toujours instable . Uniquement dans des conditions initiales spécialement sélectionnées à l'asymptoteη =0 le système s’approchera d’un état d’équilibre. Cependant, cela ne contredit pas l’affirmation sur l’instabilité du système. Si on compte, que tous les états initiaux du système sur le plan de phase sont également probables, alors la probabilité d'un tel état initial qui correspond au mouvement dans la directionÀ le point singulier est égal à zéro. Par conséquent, tout mouvement réel sortira le système de l’état d’équilibre.Revenir aux coordonnéesx, y,nous obtiendrons la même image qualitative de la nature du mouvement des trajectoires autour de l'origine des coordonnées.

La frontière entre les cas considérés d'un nœud et d'une selle est le cas Quand l'un des indicateurs caractéristiques, par exemple λ 1 , disparaît, ce qui se produit lorsque le déterminant du système- expression ad-bc=0(voir formule 4.8 ). Dans ce cas, les coefficients des membres droits des équations (4.4) sont proportionnels les uns aux autres:

et le système a pour états d'équilibre tous les points de la droite:

Les courbes intégrales restantes sont une famille de droites parallèles avec un coefficient angulaire , le long duquel les points représentatifs se rapprochent de l'état d'équilibre ou s'en éloignent, en fonction du signe de la racine seconde de l'équation caractéristique λ 2 = a+d.(Fig.4.7 ) Dans ce cas, les coordonnées de l'état d'équilibre dépendent de la valeur initiale des variables.

Racines λ 1 , λ 2 – complexeconjuguer

Dans ce cas, pour de vraiX Et oui nous allons avoir des conjugués complexes ξ , η (4.10) . Cependant, en introduisant une autre transformation intermédiaire, il est également possible dans ce cas de réduire la considération à une véritable transformation linéaire homogène. Mettons:

(4.16)

Où un B, Et toi, v – valeurs réelles. On peut montrer que la transformation dex,yÀ toi, v est, sous nos hypothèses, réel, linéaire, homogène avec un déterminant différent de zéro. Grâce aux équations(4.10, 4.16) on a :

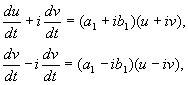
où

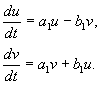(4.17)

Diviser la deuxième des équations par la première, on a:

qui est plus facile à intégrer, si on passe au système de coordonnées polaires (r, φ ) . Après remplacement on arrive d'où :

.(4.18)

Ainsi, sur le plan de phasetoi, vnous avons affaire à une famille de spirales logarithmiques dont chacune apoint asymptotique à l’origine.Un point singulier, qui est le point asymptotique de toutes les courbes intégrales ayant la forme de spirales, niché dans chacunmon ami, ça s'appelle se concentrer ( Figure 4.8 ) .

Considérons la nature du mouvement du point représentatif le long des trajectoires de phase. En multipliant la première des équations (4.17) partoi, et le deuxième sur v et en ajoutant, on obtient :

Où

Laisser un 1 < 0 (un 1 = Concernantλ ) . Le point représentatif se rapproche alors continuellement de l'origine des coordonnées sans l'atteindre à un instant fini. Cela signifie que les trajectoires des phases sont des spirales torsadées et correspondent à des oscillations amorties. variables. Ce - concentration constante .

Dans le cas d'un foyer stable, comme dans le cas d'un nœud stable, non seulement la condition de Lyapunov est satisfaite, mais également une exigence plus stricte. À savoir, pour tout écart initial, le système reviendra, au fil du temps, aussi près que souhaité de la position d’équilibre. Une telle stabilité, dans laquelle les écarts initiaux non seulement n'augmentent pas, mais décroissent, tendant vers zéro, est appelée stabilité absolue .

Si dans la formule (4.18) un 1 >0 , alors le point représentatif s'éloigne de l'origine, et nous avons affaire à mise au point instable . Lorsque vous quittez un aviontoi, vau plan de phaseX, ouiles spirales resteront également des spirales, mais seront déformées.

Considérons maintenant le cas oùun 1 =0 . Trajectoires de phase dans l'aviontoi, vil y aura des cercles qui dans l'avionx,ycorrespondent à des ellipses:

Ainsi, quandun 1=0 via un point spécialx= 0, y= 0 aucune courbe intégrale ne la traverse. Un tel point singulier isolé, près duquel les courbes intégrales sont des courbes fermées, en particulier des ellipses encastrées les unes dans les autres et entourant le point singulier, est appelé centre.

Ainsi, six types d'états d'équilibre sont possibles, selon la nature des racines de l'équation caractéristique (4.7). Vue des trajectoires de phases sur un avion x, y pour ces six cas est illustré à la Fig. 4.9.

Riz. 4.9.Types de portraits de phase au voisinage d'un état stationnaire pour un système d'équations linéaires (4.4).

Les cinq types d’états d’équilibre sont approximatifs ; leur caractère ne change pas avec des changements suffisamment faibles dans les membres droits des équations (4.4). Dans ce cas, les changements non seulement dans les membres droits, mais aussi dans leurs dérivées du premier ordre devraient être faibles. Le sixième état d’équilibre – le centre – n’est pas brutal. Avec de petits changements dans les paramètres du côté droit des équations, cela devient un foyer stable ou instable.

Diagramme de bifurcation

Introduisons la notation suivante :

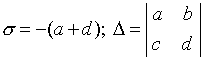. (4.11)

L’équation caractéristique s’écrira alors :

. (4.12)

Considérons un plan avec des coordonnées cartésiennes rectangulaires s , D et marquez dessus les zones correspondant à l'un ou l'autre type d'état d'équilibre, qui est déterminé par la nature des racines de l'équation caractéristique

.(4.13)

La condition de stabilité de l'état d'équilibre sera la présence d'une partie réelle négative de yje 1 et je 2 . Une condition nécessaire et suffisante pour cela est la réalisation des inégalitéss > 0, D > 0 . Dans le diagramme (4.15), cette condition correspond à des points situés dans le premier quart du plan paramètre. Un point singulier sera un focus sije 1 et je 2 complexe. Cette condition correspond aux points du plan pour lesquels , ceux. points entre deux branches d'une paraboles 2 = 4 D. Points d'essieu s = 0, D>0, correspondent à des états d’équilibre de type centre. De même,je 1 et je 2 - sont valables, mais de signes différents, c'est-à-dire un point singulier sera une selle si D<0, etc. En conséquence, nous obtiendrons un diagramme de la partition du plan paramètre s, D, en zones correspondant à différents types d’états d’équilibre.

Riz. 4.10. Diagramme de bifurcation

pour un système d'équations linéaires 4.4

Si les coefficients du système linéaire a B c d dépendent d'un certain paramètre, puis lorsque ce paramètre change, les valeurs changeront égalements , D . En franchissant les frontières, le caractère du portrait de phase change qualitativement. Par conséquent, ces limites sont appelées limites de bifurcation - sur les côtés opposés de la frontière, le système présente deux portraits de phase topologiquement différents et, par conséquent, deux types de comportement différents.

Le diagramme montre comment de tels changements peuvent se produire. Si l'on exclut les cas particuliers - l'origine des coordonnées - alors il est facile de voir que la selle peut se transformer en nœud, stable ou instable lors du franchissement de l'axe des ordonnées. Un nœud stable peut aller soit en selle, soit en foyer stable, etc. A noter que les transitions nœud stable - foyer stable et nœud instable - foyer instable ne sont pas des bifurcations, puisque la topologie de l'espace des phases ne change pas. Nous parlerons davantage de la topologie de l'espace des phases et des transitions de bifurcation dans la leçon 6.

Lors des transitions de bifurcation, la nature de la stabilité d'un point singulier change. Par exemple, une mise au point stable au centre peut se transformer en une mise au point instable. Cette bifurcation est appelée Bifurcation Andronov-Hopf par les noms des scientifiques qui l'ont étudié. Lors de cette bifurcation dans les systèmes non linéaires, un cycle limite naît et le système devient auto-oscillant (voir leçon 8).

Exemple. Système de réaction chimique linéaire

Substance X s'écoule de l'extérieur à vitesse constante, se transforme en substance Y et à une vitesse proportionnelle à la concentration de la substance Oui, est retiré de la sphère de réaction. Toutes les réactions sont du premier ordre, à l’exception de l’afflux de substance venant de l’extérieur, qui est d’ordre zéro. Le schéma de réaction ressemble à :

(4.14)

et est décrit par le système d'équations :

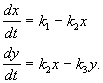(4.15)

On obtient des concentrations stationnaires en assimilant les membres droits à zéro :

.(4.16)

Considérons le portrait de phase du système. Divisons la deuxième équation du système (4.16) par la première. On a:

.(4.17)

L'équation (4.17) détermine le comportement des variables sur le plan de phase. Construisons un portrait de phase de ce système. Commençons par dessiner les principales isoclines sur le plan de phase. Équation de l'isocline des tangentes verticales :

Équation de l'isocline des tangentes horizontales :

Le point singulier (état stationnaire) se situe à l'intersection des isoclines principales.

Déterminons maintenant à quel angle les axes de coordonnées coupent les courbes intégrales.

Si x= 0, alors.

Ainsi, la tangente de la tangente aux courbes intégrales y=y(x), coupant l'axe des ordonnées x=0, est négatif dans le demi-plan supérieur (rappelons que les variables x, y ont des valeurs de concentration, et donc nous ne nous intéressons qu'au quadrant supérieur droit du plan de phase). Dans ce cas, la tangente de l’angle tangent augmente avec la distance à l’origine.

Considérons l'axe y= 0. Au point où cet axe coupe les courbes intégrales, celles-ci sont décrites par l'équation

À la tangente de la pente des courbes intégrales traversant l'axe des abscisses est positive et augmente de zéro à l'infini avec l'augmentation X.

À .

Puis, avec une nouvelle augmentation, la tangente de l'angle d'inclinaison diminue en valeur absolue, reste négative et tend vers -1 à X ® ¥ . Connaissant la direction des tangentes aux courbes intégrales sur les isoclines principales et sur les axes de coordonnées, il est facile de construire l'image complète des trajectoires de phase.

Établissons la nature de la stabilité du point singulier à l'aide de la méthode de Lyapunov. Le déterminant caractéristique du système a la forme :

.

En développant le déterminant, on obtient l'équation caractéristique du système : , c'est à dire. Les racines de l’équation caractéristique sont toutes deux négatives. Par conséquent, l’état stationnaire du système est un nœud stable. Dans ce cas, la concentration de la substance X tend vers un état stationnaire toujours de manière monotone, la concentration de la substance Y peut passer par min ou max. Les modes oscillatoires sont impossibles dans un tel système.

Point singulier

en mathématiques.

1) Un point singulier d'une courbe définie par l'équation F ( x, y) = 0, - point M 0 ( x 0 , oui 0), dans laquelle les deux dérivées partielles de la fonction F ( x, y) aller à zéro :

Sinon toutes les dérivées partielles secondes de la fonction F ( x, y) au point M 0 sont égaux à zéro, alors les O. t. sont appelés doubles. Si, avec les dérivées premières qui disparaissent au point M0, toutes les dérivées secondes, mais pas toutes les dérivées troisièmes, disparaissent, alors l'équation est appelée triple, etc. Lorsqu'on étudie la structure d'une courbe proche d'un double O.t., le signe de l'expression joue un rôle important

Si Δ > 0, alors l'espace ouvert est dit isolé ; par exemple, à la courbe oui 2 - x 4 + 4x 2= 0 l'origine des coordonnées est un O. t. isolé (voir. riz. 1 ). Si Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - un 4= 0 l'origine des coordonnées est le nœud O. t. (voir. riz. 2 ). Si Δ = 0, alors le point général de la courbe est soit isolé, soit caractérisé par le fait que différentes branches de la courbe ont une tangente commune en ce point, par exemple : a) point de rebroussement de 1ère espèce - différentes branches de les courbes sont situées sur les côtés opposés de la tangente commune et forment un point, comme une courbe oui 2 - x 3= 0 (voir riz. 3 , un); b) point de rebroussement de 2ème espèce - différentes branches de la courbe sont situées d'un côté de la tangente commune, comme une courbe (y-x 2)2-x5= 0 (voir riz. 3 , b); c) point d'auto-touche (pour une courbe oui 2 - x 4= 0 l'origine est le point de contact personnel ; (cm. riz. 3 , V). Outre l'O.t. indiqué, il existe de nombreux autres O.t. portant des noms spéciaux ; par exemple, le point asymptotique est le sommet d'une spirale avec un nombre infini de tours (voir. riz. 4 ), point de terminaison, point d'angle, etc.

2) Un point singulier d'une équation différentielle est le point auquel le numérateur et le dénominateur du côté droit de l'équation différentielle disparaissent simultanément (voir Équations différentielles)

où P et Q sont des fonctions continûment différentiables. En supposant que O. t. est situé à l'origine des coordonnées et en utilisant la formule de Taylor (voir formule de Taylor), nous pouvons représenter l'équation (1) sous la forme

où P 1 ( x, y) et Q 1 ( x, y) - infinitésimal par rapport à

À savoir, si λ 1 ≠ λ 2 et λ 1 λ 2 > 0 ou λ 1 = λ 2, alors O. t. est un nœud ; toutes les courbes intégrales passant par des points d'un voisinage suffisamment petit d'un nœud y entrent. Si λ 1 ≠ λ 2 et λ 1 λ 2 i β, α ≠ 0 et β ≠ 0, alors le point général est un foyer ; toutes les courbes intégrales passant par des points dans un voisinage suffisamment petit du foyer représentent des spirales avec un nombre infini de tours dans n'importe quel voisinage arbitrairement petit du foyer. Si finalement λ 1,2 = ± jeβ, β ≠ 0, alors le caractère de O. t. n'est pas déterminé uniquement par des termes linéaires dans les développements de P ( x, y) et Q ( x, y), comme ce fut le cas dans toutes les affaires ci-dessus ; ici, O. t. peut être un foyer ou un centre, ou il peut avoir plus de nature complexe. Au voisinage du centre, toutes les courbes intégrales sont fermées et contiennent le centre à l’intérieur d’elles. Ainsi, par exemple, le point (0, 0) est un nœud pour les équations à" = 2u/x(λ 1 = 1, λ 2 = 2 ; voir riz. 5 , a) et oui" = u/x(λ 1 = λ 2 = 1 ; voir riz. 5 , b), selle pour l'équation y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. riz. 6 ), le point central de l'équation y" =(x + y) / (x - y) (λ 1 = 1 - je, λ 2 = 1 + je; cm. riz. 7 ) et le centre de l'équation y" = -x/y(λ 1 = -je, λ 2 = je; cm. riz. 8 ).

Si x, y) et Q ( x, y) analytique, quartier O. t. ordre supérieur peut être divisé en régions : D 1 - rempli de courbes intégrales, les deux extrémités incluses dans l'O. t. (régions elliptiques), D 2 - rempli de courbes intégrales, une extrémité incluse dans l'O. t. (régions paraboliques), et D 3 - régions , délimitées par deux courbes intégrales incluses dans la théorie générale, entre lesquelles se situent des courbes intégrales de type hyperbole (régions hyperboliques) (voir riz. 9 ). S'il n'y a pas de courbes intégrales incluses dans un point général, alors le point général est appelé point de type stable. Le voisinage d'un oscillateur stable est constitué de courbes intégrales fermées contenant en elles-mêmes une osmose, entre lesquelles se trouvent des spirales (voir Fig. riz. dix ).

L'étude des équations différentielles, c'est-à-dire essentiellement l'étude du comportement des familles de courbes intégrales au voisinage des équations différentielles, constitue une des branches de la théorie qualitative des équations différentielles et joue un rôle important dans les applications, notamment dans questions de stabilité du mouvement (travaux de A. M. Lyapunov, A. Poincaré, etc.).

3) Un point singulier d'une fonction analytique à valeur unique est le point auquel l'analyticité de la fonction est violée (voir Fonctions analytiques). S'il existe un quartier d'O. t. un, libre des autres O. t., puis pointez UN appelé isolé O. t. Si UN- une théorie générale isolée et il existe un a fini est appelée théorie générale amovible. En changeant de manière appropriée la définition d'une fonction en un point a (ou en la redéfinissant à ce point, si la fonction en ce point n'est pas définie du tout), à savoir, en supposant F(un)=b, il est possible d'y parvenir un deviendra un point ordinaire de la fonction corrigée. Par exemple, point z= 0 est un O.t. amovible pour la fonction f 1 ( z) = F(z), Si z≠ 0, et F 1 (0), = 1, point z= 0 est un point ordinaire [ F 1 (z) est analytique au point z= 0]. Si UN- un O. t. et a isolés sont appelés un pôle ou un point essentiellement singulier d'une fonction F(z), si la série Laurent) fonctionne F(z) au voisinage d'un O. t. isolé ne contient pas de puissances négatives z - une, Si UN- O. t. amovible, contient un nombre fini de degrés négatifs z - une, Si UN- pôle (dans ce cas l'ordre du pôle R. défini comme plus haut degré a est un point essentiellement singulier. Par exemple, pour la fonction

p = 2, 3, …)

point z= 0 est le pôle d'ordre R., pour la fonction

point z= 0 est un point essentiellement singulier.

A la limite du cercle de convergence d'une série entière il doit y avoir au moins un O.t. de la fonction représentée dans ce cercle par la donnée série de puissance. Tous les points limites du domaine d'existence d'une fonction analytique unique (frontière naturelle) sont les limites de cette fonction. Ainsi, tous les points du cercle unité | z| = 1 sont spéciaux à la fonction

Pour une fonction analytique à valeurs multiples, le concept de « O. T." Plus difficile. En plus du O. t., dans les feuillets individuels de la surface de Riemann d'une fonction (c'est-à-dire le O. t. des éléments analytiques à valeur unique), chaque point de branchement est également le O. t. de la fonction. Les points de branchement isolés d'une surface de Riemann (c'est-à-dire des points de branchement tels que dans leur voisinage il n'y a aucune autre fonction O. t. dans aucune feuille) sont classés comme suit. Si a est un point de branchement isolé d’ordre fini et qu’il existe un a fini, on l’appelle un pôle critique. Si UN- un point de branchement isolé d'ordre infini et a est appelé un O.t transcendantal. Tous les autres points de branchement isolés sont appelés points critiques essentiellement singuliers. Exemples: point z= 0 est le point critique ordinaire de la fonction f ( z) = journal z et le point critique essentiellement singulier de la fonction F (z) = péché ln z.

Tout problème général, à l'exception d'un problème amovible, est un obstacle à la continuation analytique, c'est-à-dire que la continuation analytique le long d'une courbe passant par un problème général irréductible est impossible.

Grand Encyclopédie soviétique. - M. : Encyclopédie soviétique. 1969-1978 .

Voyez ce qu'est un « point singulier » dans d'autres dictionnaires :

Points ici. Voir aussi point singulier ( équations différentielles). Une caractéristique ou une singularité en mathématiques est un point auquel un objet mathématique (généralement une fonction) n'est pas défini ou a un comportement irrégulier (par exemple, un point auquel... ... Wikipedia

Une fonction analytique est un point auquel les conditions d’analyticité sont violées. Si la fonction analytique f(z) est donnée partout dans un certain voisinage du point z0... Encyclopédie physique

Une fonction analytique est le point auquel l'analyticité de la fonction est violée... Grand dictionnaire encyclopédique

point singulier- - [Ya.N.Luginsky, M.S.Fezi Zhilinskaya, Yu.S.Kabirov. Dictionnaire anglais-russe du génie électrique et du génie électrique, Moscou, 1999] Thèmes du génie électrique, concepts de base EN point singulier... Guide du traducteur technique

1) Une fonction analytique f(z) est un obstacle à la continuation analytique d'un élément d'une fonction f(z) d'une variable complexe z le long de tout chemin sur le plan de cette variable. Soit la fonction analytique f(z) définie par certains... ... Encyclopédie mathématique

Fonction analytique, le point auquel l'analyticité de la fonction est violée. * * * POINT UNIQUE POINT UNIQUE d'une fonction analytique, le point auquel l'analyticité de la fonction est violée... Dictionnaire encyclopédique

point singulier- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. point singulier vok. singulärer Punkt, m rus. point singulier, f pranc. point particulier, m; point singulier, m … Automatikos terminų žodynas

point singulier- ypatingasis taškas statusas T sritis fizika atitikmenys: engl. point singulier vok. singulärer Punkt, m rus. point singulier, f pranc. point singulier, m… Fizikos terminų žodynas

Concepts et définitions de base :

Le zéro de la fonction analytique f(z) est le point « a » pour lequel f(a)=0.

Un zéro d'ordre « n » d'une fonction f(z) est un point « a » si fn(a)¹0.

Un point singulier « a » est appelé point singulier isolé d'une fonction f(z) s'il existe un voisinage de ce point dans lequel il n'y a pas de points singuliers autres que « a ».

Il existe trois types de points singuliers isolés : .

1 points singuliers amovibles ;

3 points essentiellement singuliers.

Le type de point singulier peut être déterminé en fonction du comportement d'une fonction donnée au point singulier trouvé, ainsi qu'à partir de la forme de la série de Laurent obtenue pour la fonction au voisinage du point singulier trouvé.

Déterminer le type d'un point singulier par le comportement de la fonction sur celui-ci.

1. Points singuliers amovibles.

Un point singulier isolé a d'une fonction f(z) est dit amovible s'il existe une limite finie.

2.Pôles.

Un point singulier isolé a d'une fonction f(z) est appelé pôle si .

3. Points essentiellement singuliers.

Un point singulier isolé a d'une fonction f(z) est appelé un point essentiellement singulier s'il n'existe ni fini ni infini.

La relation suivante existe entre les zéros et les pôles de la fonction.

Pour que le point a soit un pôle d'ordre n de la fonction f(Z), il faut et suffisant que ce point soit un zéro d'ordre n pour la fonction .

Si n=1 le pôle est dit simple.

Définition: Un point singulier isolé de nature sans ambiguïté s'appelle :

a) amovible si l'essentiel de la décomposition est manquant ;

b) un pôle, si la partie principale contient un nombre fini de termes ;

c) un point essentiellement singulier si la partie principale contient un nombre infini de termes.

a) Ainsi, au voisinage d'un point singulier amovible, l'expansion a la forme :

il exprime la fonction en tous points du cercle |z-a|

Au centre z=a l'égalité n'est pas vraie, car la fonction en z=a a une discontinuité et le côté droit est continu. Si la valeur de la fonction au centre est modifiée, en la prenant égale à la valeur du côté droit, alors l'espace sera éliminé - d'où le nom - amovible.

b) Au voisinage d'un pôle d'ordre m, le développement en série de Laurent a la forme :

c) A proximité d'un simple poteau

Déductions et formules pour les calculer.

Le résidu d'une fonction analytique f(z) en un point singulier isolé z 0 est un nombre complexe égal à la valeur de l'intégrale , pris dans le sens positif le long du cercle L de centre au point z 0 situé dans le domaine d'analyticité de la fonction f(z) (c'est-à-dire dans l'anneau 0<|z-z0|

Le résidu de la fonction f(z) en un point singulier isolé z 0 est désigné par le symbole Res f(z 0) ou Res (f(z); z 0). Ainsi,

Rés f(z 0)= . (22.15.1)

Si on met n=-1 dans la formule (22.15.1), on obtient :

C-1 =

ou Res f(z 0)= C -1 ,

ceux. le résidu de la fonction f(z) par rapport au point singulier z 0 est égal au coefficient du premier terme d'exposant négatif dans le développement de la fonction f(z) dans la série de Laurent.

Calcul des déductions.

Points singuliers réguliers ou amovibles. Évidemment, si z=z 0 est un point singulier régulier ou amovible de la fonction f(z), alors Res f(z 0)=0 (le développement de Laurent dans ces cas n'a pas la partie principale, donc c-1=0) .

Pôle. Soit le point z 0 un pôle simple de la fonction f(z). Alors la série de Laurent pour la fonction f(z) au voisinage du point z 0 a la forme :

D'ici

Donc, en passant cette égalité à la limite en z --z 0, on obtient

Rés f(z0)=

Point essentiellement spécial. Si le point z 0 est un point essentiellement singulier de la fonction f(z), alors pour calculer le résidu de la fonction en ce point, le coefficient c-1 dans le développement en série de Laurent de la fonction est généralement directement déterminé.

Classement des événements. Somme, produit d'événements, leurs propriétés, représentation graphique.

Les événements sont divisés en :

1. Aléatoire

2. Fiable

3. Impossible

Fiable est un événement qui se produit nécessairement dans des conditions données (la nuit suit le matin).

Un événement aléatoire est un événement qui peut se produire ou non (réussite d'un examen).

Un événement impossible est un événement qui ne se produira pas dans des conditions données (sortir un crayon vert d'une boîte contenant uniquement des rouges).

Laisser zq est le point singulier de la fonction /(r), t.s. f(z) mais il est analytique à ce stade (en particulier, il peut ne pas y être défini). S'il y a un tel quartier perforé du point zq (c'est-à-dire l'ensemble O z - zq f(z) est aialitique, alors zo appelé point singulier isolé les fonctions f(z). Cette définition reste la même dans le cas de zn = oo, si l'iode est percé par le voisinage du point zq = oo comprendre ensemble z> je - l'extérieur d'un cercle avec son centre à l'origine. En d'autres termes, un point particulier zq est dit isolé s’il existe un voisinage de ce point dans lequel l’ensemble des autres points singuliers autres que zq. Dans tout ce qui suit nous ne considérerons que des points singuliers présentant un caractère unique (la fonction f(z) supposé sans ambiguïté).

En fonction du comportement de la fonction f(z)à z -> zq Il existe trois types de points singuliers. Point singulier isolé fonctions zq f(z) appelé:

1) point singulier amovible, s'il existe une limite finie

2) pôle, s'il y a une limite

3) essentiellement un point particulier, Si f(z) n’a ni limite finie ni infinie à z-> zq.

Exemple 26.1. Montrons que les trois types de points singuliers sont réalisés. Considérons F(z)= Point zq = 0 est isolé

point particulier de cette fonction. En utilisant la formule (22.12), on obtient le développement

d'où il résulte qu'il existe lim fi(z)= 1. Donc zq = 0 est

est un point singulier amovible de la fonction fi(z).

Fonction f‘j(z) =---a un poteau en un point zo= 1 parce que

2 r" X

Considérons maintenant la fonction )з(z)= e 1 ^ r et montrer que zo = O est un point essentiellement singulier de cette fonction. En s'efforçant z mettre à zéro le long de l'axe réel les limites gauche et droite de la fonction /z (z) différent : lim Avec 1 / 1 = 0, limite s 1 /* = os. Cela implique,

x->0-0 x->0+O

Quoi f:je(z) n'a ni limite finie ni infinie en 2 -> Oh, c'est vrai. zq = O est un point essentiellement singulier de cette fonction. (Notez que comme le point tend z - jeà zéro le long de la fonction de l'axe imaginaire

n'a aucune limite.)

Il existe bien entendu des points singuliers non isolés. Par exemple. la fonction a des pôles en des points z n = -, P.= ±1, ±2,...

Ainsi, Zq = 0 est un point singulier non isolé de cette fonction : dans tout voisinage (aussi petit soit-il) de ce point il existe d'autres points singuliers gp.

Laisser zo- point singulier isolé fini d'une fonction f(z). Alors f(z) est similaire dans certains quartiers perforés du point 0 Zo zo ce quartier peut être considéré comme un anneau de rayon interne r = 0. D'après le théorème 25.1, dans le quartier considéré la fonction f(z) peut être étendu en une série Laurent (25.2). Nous allons montrer que le comportement de la fonction à 2 -> zq (c'est à dire le type de point singulier zo) dépend du type de la partie principale de l'expansion (25.2) ; Cette circonstance explique l'origine du terme « partie principale ».

Théorème 2G.2. Un point singulier isolé zo d'une fonction f(z) est amovible si et seulement si le développement de Lorapov dans un voisinage perforé de ce point a oid

ceux. se compose uniquement de la bonne partie, et tous les coefficients de la partie principale sont égaux à la balle.

Preuve. 1. Laissez zo- point singulier amovible. Montrons que le développement de Laurent de la fonction f(z) a la forme (26.1). Depuis le point particulier zo amovible, alors il y a une limite finie f(z) = UNE. Ainsi, f(z) est délimité dans un voisinage perforé du point 0 z - zq zo, ceux. )(z) pour tout le monde z de ce voisinage. Prenons n'importe lequel R. U р /?|, et utiliser les formules (25.3) pour les coefficients de la série Laurent :

Pour les coefficients de la partie principale de l'expansion n =- 1,-2,... Pour de telles valeurs P. nous avons p ~ p-e 0 à R.-> 0. Puisque la valeur R. peut être choisi arbitrairement petit, alors Monsieur~" peut être aussi petit que souhaité. Depuis |s t,| ^ M~p et c" ne dépendent pas de p, alors c" = 0 à Et= - 1, -2,..., c'est ce qu'il fallait prouver.

2. Supposons maintenant que le développement de Laurent a la forme (26.1). La série (26.1) est une série entière et. par conséquent, il converge non seulement dans la zone perforée, mais également dans tout le voisinage z-zq y compris le point zo; son montant S(z) est analytique à z et S(z) = )(z)à 0 z - zo R. Il existe donc une limite finie lim )(z)= Pt 5(g) = 5(th) - Donc le point singulier zq

Z->Zo Z-*Zo

amovible. Le théorème a été prouvé.

Commentaire. De la preuve du théorème il résulte que dans un voisinage perforé 0 z - zo d'un point singulier amovible la fonction f(z) coïncide avec la fonction 5(r), qui est analytique dans tout le voisinage z - zo. Par conséquent, si nous posons /(th) = S(zq), puis, sans changer les valeurs de la fonction f(z) en tout point du voisinage perforé, nous rendrons cette fonction analytique en Go, c'est-à-dire « Éliminons » cette fonctionnalité. Ceci explique le terme « fonctionnalité amovible ». Il est naturel de considérer de tels points comme des points réguliers et non singuliers de la fonction f(z).

Prenons par exemple la fonction

Dans l'exemple 26.1, il a été montré que Pm Nr) = 1. c'est-à-dire point singulier

zq = 0 amovible. En mettant /i(0) = 1, nous éliminons ainsi la singularité et obtenons une fonction analytique au point zq = 0 (et dans tout le plan C).

Caractérisons maintenant les pôles en termes de développements de Laurent.

Théorème 26.3. Un point singulier isolé Zo d'une fonction f(z) est un pôle si et seulement si, lorsque la partie principale du développement de Laurent de centre Zq n'a qu'un nombre fini de points distincts

à partir de coefficients nuls avec n :

Preuve. 1. Laissez zq - pôle, c'est-à-dire lim/( z) = oh.

Montrons que le développement de Laurent de la fonction f(z) a la forme (2G.2). Depuis lim f(z)= oh. alors il y a un voisinage perforé du point

ki zq. où f(z) est analytique et n’a pas de zéros. Alors la fonction g(z) = 1 /f(z) sera également analytique dans ce quartier perforé, et lim g(z)= 0. Par conséquent, Zo est amovible *-? *0

point singulier de la fonction g(z). Définissons g(z)à ce point zo, en mettant g(zo)= 0. Alors g(z) deviendra analytique dans tout le voisinage du point (non percé) z 0 , et z 0 sera son zéro isolé. Notons par N multiplicité (ordre) de ce zéro. Comme cela a été montré au §23, au voisinage du point fonction zq g(z) peut être représenté sous la forme (voir (23.2))

et (z$)f 0 et y>(z) est analytique dans un certain voisinage du point zo- Parce que IP(z) continu en un point zo Et g>(zo) Ф 0" alors IP(z) n'a pas de zéros dans certains voisinages de ce point. Donc fonction 1 /-p(z) sera également analytique dans ce quartier et, par conséquent, s'y développera dans une série de Taylor :

En ouvrant les parenthèses et en changeant les désignations des coefficients, nous écrivons le dernier développement sous la forme

où c_jv = 1>de 0. Ainsi, la partie principale du développement de Laurent de la fonction /(r) ne contient qu'un nombre fini de termes ; nous sommes arrivés à l'égalité souhaitée (26.2).

2. Laisser entrer le voisinage perforé des points ème fonction )(z) est représenté par le développement de Laurent (26.2) (pour une forme plus détaillée, voir (26.3)), dont la partie principale ne contient qu'un nombre fini de termes, et Avec- d" F 0. Il faut prouver que Zq - pôle de fonction f(z). Multiplier l'égalité (26.3) par (G - g o) iV , on obtient la fonction

La série dans (26.4) est une série entière qui converge vers une fonction analytique non seulement dans le point perforé, mais aussi dans tout le voisinage du point Zq. Donc la fonction h(z) deviendra analytique dans ce quartier si nous le définissons plus en détail en mettant h(zo)= s_dg F 0. Alors

Ainsi, le point th est un pôle, et le théorème 26.3 est prouvé.

Multiplicité (ordre) de la fonction zéro g(z)= 1//(g) est appelé ordre des pôlesème fonction /(r). Si N- l'ordre du pôle de th, alors g(z)= (g- Zo) Nip(z), et aller) F 0, et, comme le montre la première partie de la preuve du théorème 26.3, le développement de la fonction /(r) a la forme (26.3), où c_/v F 0. Inversement, si /(r) est développé dans la série (26.3) et e-i F 0, alors

c.t. N- ordre du pôle de la fonction /(r). Ainsi, ordre des pôles de la fonction zq/(G) égal au numéro du coefficient non nul le plus élevé de la partie principale du développement de Laurent au voisinage perforé du point zq(c'est-à-dire égal à ce nombre N, qu'est-ce que c'est F 0 et Esp.= 0 à P. > N).

Démontrons l'énoncé suivant, qui convient aux applications.

Corollaire 26.4. Le point zq est un pôle d'ordre N de la fiction/(G) alors et seulement quand/(G) représentable sous la forme

où h(z) est une fonction analytique au voisinage du pointème et h(zo)f 0.

Preuve. Fonction cp(z) = l/h(z) est analytique dans un certain voisinage du point h. La condition du corollaire 26.4 est équivalente à la suivante :

C'est pourquoi zq - multiplicité nulle N les fonctions g(z). et donc le pôle de multiplicité N fonctions /(2).

II Exemple 26.5. Trouver des points singuliers isolés d'une fonction et déterminer leur type.

Solution : Les points auxquels (z 2 + 1 )(z+ Z) 2 = 0. Si z 2 L- 1 = 0, alors 2 = ± g Si (z 4- 3) 2 = 0, alors z= -3. La fonction possède donc trois points singuliers z= g, 22 = -g, Z3 = - 3. Considérez z:

G - pôle de premier ordre (nous avons utilisé le corollaire 26.4). On peut prouver de la même manière que 22 = -jeégalement un pôle de premier ordre. Pour 2z on a :

Passons maintenant à des points essentiellement singuliers.

Théorème 26.6. Un point singulier isolé zq d'une fonction f(z) est essentiellement singulier si et seulement si la partie principale du développement de Laurent de centre zq a une infinité de distincts. zéro, coefficients de p.

Preuve. Le théorème 26.6 découle directement des théorèmes 26.2 et 26.3. En effet, si le point zq est essentiellement spécial, alors la partie principale du développement de Laurent ne peut pas être absente ou contenir un nombre fini de termes (sinon le point Zq sera soit amovible, soit un poteau). Par conséquent, le nombre de termes dans la partie principale doit être infini.

Inversement, si la partie principale contient une infinité de termes, alors Zq ne peut être ni une pointe amovible ni un poteau. Il s’ensuit que ce point est essentiellement particulier.

Selon la définition, un point essentiellement singulier se caractérise par le fait que la fonction /(2) n'a ni limite finie ni infinie pour z ->zq. Une idée plus complète de l'irrégularité du comportement d'une fonction au voisinage d'un point essentiellement singulier est donnée par le théorème suivant.

Théorème 26.7 (théorème de Sokhotsky). Si zq est essentiel aux personnes, l’intérêt de la fonction f(z), alors pour tout nombre complexe L, dont A = Oh, il existe une séquence de points z n telle que z n -> zo et lim f(zn) = UN.

p->os

Preuve. Considérons d'abord le cas UNE = ouh. Dans la première partie de la preuve du théorème 2G.2 nous avons établi que si f(z) est délimité dans un voisinage perforé du point r, alors tous les coefficients c", n = - 1,- 2,... de la partie principale sont égaux à zéro (et donc la singularité en aller est amovible). Puisque par condition th est un point singulier essentiel, alors dans tout voisinage perforé du point th la fonction f(r) est illimitée. Prenons un voisinage fort 0 Z tel que f(zi) > 1 (si |/(r)| z - zo I/2 il y a un point z-2 , dans lequel |/(yy)| > 2, etc. : dans le quartier perforé O 71. Il est évident que r„ -e go et lim /(r“) = oo. Ainsi, dans le cas A = oo, le Théorème 26.7

éprouvé.

Laisse-le maintenant Un F ouh. Supposons d'abord qu'il existe un voisinage perforé 0

= -aaa---- sera analytique dans ce quartier perforé et, par conséquent,

/(G) - UN

Par conséquent, go est un point singulier isolé de la fonction Φ(r). Nous allons vous montrer. que r est un point essentiellement singulier de Φ(r). Cela n'est peut-être pas vrai. Alors il existe une limite lim Ф(r), finie ou infinie. Pendant un certain temps

/(r) = A + , alors il y a aussi Hsh /(r), ce qui contredit la condition

F(g) ~ :-*z 0

Je vois le théorème. Ainsi, r0 est un point essentiellement singulier de la fonction Φ(r). D'après ce qui a été prouvé ci-dessus, il existe une suite de points r n telle que r n th et lim Ф(r n) = oo. D'ici

Nous avons prouvé l’énoncé requis sous l’hypothèse que /(r) FA dans un quartier perforé du point aller- Supposons maintenant que cela soit faux, c'est-à-dire dans tout voisinage perforé arbitrairement petit du point où il existe un tel point G", que /(r") = L. Alors pour tout P. dans le quartier perforé 0 f(z u) = A. Ainsi, l'énoncé souhaité est vrai P.-yuo

dans tous les cas, et le théorème 26.7 est prouvé.

D'après le théorème 26.7 (Sokhotsky), dans tout voisinage perforé (arbitrairement petit) d'un point essentiellement singulier, la fonction /(r) prend des valeurs arbitrairement proches de n'importe quel nombre du plan complexe étendu C.

Pour étudier des points singuliers isolés, les développements de Taylor déjà connus des fonctions élémentaires de base sont souvent utiles.

Exemple 2G.8. Déterminer le type de point singulier zq = 0 pour la fonction

Résolu et e. Développons le numérateur et le dénominateur en une série de Taylor en puissances de g. En remplaçant dans (22.11) 3 z au lieu de r et en soustrayant 1, on obtient

En utilisant (22.12), on obtient le développement du dénominateur :

Les séries de ces développements convergent dans tout le plan complexe €. Nous avons

et /2(2) sont anaritiques au voisinage du point zo = 0 (et même dans tout le plan) et /2(20) F 0, alors h(z) est également analytique dans un certain voisinage du point gF 0. D'après le corollaire 26.4, le point Zo = 0 est le pôle de l'ordre N=4.

II Exemple 26.9. Trouver les points singuliers d'une fonction f(z)= sin j - et déterminez leur type.

R e in e i e. La fonction a un seul point singulier fini zq = 1. En d'autres points de C la fonction w =--- analytique; d'où la fonction sin w sera analytique.

En remplaçant - au lieu de r dans le développement du sinus (22.12), nous obtenons

Nous avons obtenu le développement de la fonction sin en une série de Laurent dans un voisinage perforé du point 2o = 1. Puisque le développement résultant contient une infinité de termes de puissances négatives (r - 1), alors zq = 1 est un point essentiellement singulier (dans ce cas, le développement de Laurent n'est constitué que de la partie principale, et la partie régulière est manquante).

A noter qu'il a été possible d'établir la nature de la singularité dans ce cas directement à partir de la définition, sans recourir au développement en série. En effet, il existe des séquences (r") et (2") convergeant vers zo= 1, et tel que f(z"n)= 1, /(2") = 0 (indiquez vous-même ces séquences). Donc, f(z) n'a pas de limite à z -> 1 et donc point zq - 1 est essentiellement spécial.

Introduisons la notion de développement de Laurent d'une fonction au voisinage d'un point Zq = 00 et considérons le lien entre l'expansion et la nature de la singularité à ce stade. Notez que les définitions d'un point singulier isolé et de son type (amovible, polaire ou essentiellement singulier) s'appliquent au cas zq = oc sans modifications. Mais les théorèmes 26.2. 26.3 et 26.6, liés à la nature des extensions de Laurent, doivent être modifiés. Le fait est que les membres cn(z- 2o)p. P.= -1,-2,..., partie principale, définissant « l'irrégularité » de la fonction près du point final Zq, comme 2 tend vers oo, ils se comporteront « correctement » (tendront vers 0). Au contraire, les membres de la bonne partie avec P.= 1,2,... aura tendance à oo ; ils déterminent la nature de la fonctionnalité dans Zq = oo. Par conséquent, la majeure partie de l’expansion au voisinage de oo sera constituée de termes avec des puissances positives P, et le bon - avec des négatifs.

Introduisons une nouvelle variable w = 12. Fonction télé = 1/2, étendu de sorte que u(oo) = 0, un à un et mappe le quartier de manière conforme z > R points zq = 00 au voisinage de |w| wq = 0. Si la fonction f(z) analyses dans le quartier perforé R. z Zq = oc, alors la fonction G(w) = f(l/w) sera analytique dans le grand voisinage 0 wo = 0. Puisqu'à 2 -> oo il y aura w-> 0, alors

C'est pourquoi G(w) a au point wq = 0 est une caractéristique du même type que f(z)à ce point Zq = 00. Développons la fonction G(w) en une série de Laurent dans un voisinage perforé du point wo = 0 :

Les sommes du côté droit de (26.5) représentent respectivement les parties régulière et principale du développement. Passons à la variable z, remplacement w = 1/z :

Désignation P.= -A*, 6* = 6_„ = s p et remarquant que G(l/z) = f(z), on a

La décomposition (2G.G) est appelée Développement de Laurent de la fonction f(z) dans un voisinage perforé du point zq= oh. La première somme de (2G.6) s’appelle la bonne partie, et la deuxième somme est partie principale de cette décomposition. Puisque ces sommes correspondent aux parties correctes et principales du développement (26.5), alors les analogues des théorèmes 26.2, 26.3 et 26.6 sont valables pour le développement (26.6). Ainsi, le théorème suivant sera un analogue du théorème 26.2.

Théorème 26.10. Point singulier isoléZq - Système d'exploitation (les fonctions/(G) est amovible si et seulement si l'expansion de Laurent dans un voisinage percé de ce point a la forme

c.t. se compose uniquement de la partie correcte.

Mettons /(oo) = co. Fonction définie par des séries (26.7) convergeant dans le voisinage z > R point 2o = oc, appelé analytique au point z o = oo. (Notez que cette définition est équivalente à l'analyticité de la fonction G(w) au point oh = 0.)

Exemple 26.11. Étudier le point singulier zq = oo de la fonction

Puisque la limite est finie, alors zo = oo est un point singulier amovible de la fonction /(r). Si on met /(oo) = lim J(z)= 0, alors f(z) deviendra analytique

tic au point Zo= os. Indiquons comment trouver le développement correspondant (26.7). Passons à la variable w = 1 fz. Remplacement z= 1 /?е, on obtient

(la dernière égalité est valable dans un voisinage perforé du point wо = 0, mais nous définirons plus loin (7(0) = 0). La fonction résultante a des points singuliers w =±je, w =-1/3, et au point Wq = 0 est analytique. Fonction de dépliage G(w) graduellement w(comme cela a été fait dans l'exemple 25.7) et en substituant dans la série de puissances résultante w = 1/z, on peut obtenir le développement (26.7) de la fonction f(z).

Théorème 26.3 pour le cas zo= oo sera réécrit sous la forme suivante.

Théorème 26.12. Point singulier isolé e = os la fonction f(z) est un pôle si et seulement si la partie principale du développement de Laurent (26.6) n'a qu'un nombre fini de coefficients non nuls Avec":

Ici, la série est la partie régulière et le polynôme entre parenthèses est la partie principale du développement. La multiplicité polaire en oc est définie comme la multiplicité polaire wq = 0 fonctions G(z). Il est facile de voir que la multiplicité du pôle coïncide avec le nombre N dans (26.8).

Q p | (je 2 + 1)(z+3) 2

Tâche. Montrer que la fonction f(z) =-- -- a dans

indiquer zo = oo pôle d'ordre 3.

Le théorème 26.6 sur un point essentiellement singulier peut être réécrit pour le cas zo= os presque mot pour mot, et nous ne nous attarderons pas là-dessus en détail.