Trois définitions équivalentes d'une fonction continue en un point. Fonction continue

Théorème. Laissez la fonction x=φ(t) continu en un point un, et la fonction y=f(x) continu en un point b = φ (une). Alors la fonction complexe y=f[φ(t)]=F(t) continu en un point un.

Laisser x=φ(t) Et y=f(x)- les fonctions élémentaires les plus simples, avec de nombreuses valeurs (X) les fonctions x=φ(t) est la portée de la fonction y=f(x). Comme nous le savons, les fonctions élémentaires sont continues en tout point du domaine donné. Donc, d’après le théorème précédent, la fonction complexe y=f(φ(t)), c'est-à-dire la superposition de deux fonctions élémentaires, est continue. Par exemple, une fonction est continue en tout point x ≠ 0, comme fonction complexe de deux fonctions élémentaires x=t-1 Et y = péché x. Fonctionne également y=ln péché x continue en tout point dans les intervalles (2kπ,(2k+1)π), k ∈Z (péché x>0).

1. Introduction.

2. Détermination de la continuité d'une fonction.

3. Classement des points de rupture

4. Propriétés des fonctions continues.

5. Le sens économique de la continuité.

6. Conclusion.

10.1. Introduction

Chaque fois que nous évaluons les changements inévitables dans le monde qui nous entoure au fil du temps, nous essayons d’analyser les processus en cours afin de mettre en évidence leurs caractéristiques les plus significatives. L’une des premières questions qui se posent tout au long de ce chemin est : Comment des changements caractéristiques de ce phénomène se produisent - en continu ou discrètement, c'est à dire. spasmodiquement. Le taux de change se déprécie-t-il ou s’effondre-t-il uniformément, y a-t-il une évolution progressive ou un bond révolutionnaire ? Afin d'unifier les évaluations qualitatives et quantitatives de ce qui se passe, il convient de faire abstraction du contenu spécifique et d'étudier le problème en termes de dépendance fonctionnelle. Cela peut être réalisé grâce à la théorie des limites, dont nous avons discuté dans la dernière leçon.

10.2. Définition de la continuité d'une fonction

La continuité d'une fonction est intuitivement liée au fait que son graphique est une courbe continue qui ne se rompt nulle part. Nous dessinons un graphique d’une telle fonction sans lever la plume du papier. Si une fonction est donnée dans un tableau, alors, à proprement parler, sa continuité ne peut pas être jugée, car pour une étape donnée du tableau, le comportement de la fonction dans les intervalles n'est pas défini.

En réalité, avec continuité, la circonstance suivante se produit : si les paramètres caractérisant la situation Un peu change alors Un peu la situation va changer. L’important ici n’est pas que la situation change, mais qu’elle change « un peu ».

Formulons le concept de continuité dans le langage des incréments. Laissez un phénomène être décrit par une fonction et un point un appartient au domaine de définition de la fonction. La différence s'appelle incrément d'argumentà ce point un, différence - incrément de fonctionà ce point un.

Définition 10.1.Fonction continu en un point a, s'il est défini à ce stade et qu'un incrément infinitésimal dans l'argument correspond à un incrément infinitésimal dans la fonction :

Exemple 10.1. Examinez la continuité de la fonction à ce point.

Solution. Construisons un graphique de la fonction et marquons dessus les incréments D X et D oui(Fig. 10.1).

Le graphique montre que plus l'incrément D est petit X, moins D oui. Montrons cela analytiquement. L'incrément de l'argument est égal à , alors l'incrément de la fonction à ce stade sera égal à

De là, il est clair que si , alors et :

.

Donnons une autre définition de la continuité d'une fonction.

Définition 10.2.La fonction s'appelle continu au point a si :

1) il est défini au point a et certains de ses environs ;

2) des limites unilatérales existent et sont égales entre elles :

;

3) limite de la fonction en x® a est égal à la valeur de la fonction à ce stade :

.

Si au moins une de ces conditions est violée, alors la fonction est dite subir écart.

Cette définition est opérationnelle pour établir une continuité en un point. En suivant son algorithme et en notant les coïncidences et les divergences entre les exigences de la définition et un exemple précis, nous pouvons conclure que la fonction est continue en un point.

Dans la définition 2, l’idée de proximité émerge clairement lorsque l’on introduit la notion de limite. Avec une approximation illimitée de l'argument Xà la valeur limite un, continu en un point un fonction F(X) se rapproche arbitrairement de la valeur limite F(un).

10.3. Classement des points de rupture

Les points auxquels les conditions de continuité d'une fonction sont violées sont appelés points de rupture cette fonction. Si X 0 est le point d'arrêt de la fonction ; au moins une des conditions de continuité de la fonction n'est pas remplie. Considérez l'exemple suivant.

1. La fonction est définie dans un certain voisinage du point un, mais non défini au point lui-même un. Par exemple, la fonction n'est pas définie au point un=2, subit donc une discontinuité (voir Fig. 10.2).

Riz. 10.2 Fig. 10.3

2. La fonction est définie en un point un et dans certains de ses environs, ses limites unilatérales existent, mais ne sont pas égales les unes aux autres : , alors la fonction subit une discontinuité. Par exemple, la fonction

est défini au point, mais au niveau de la fonction subit une discontinuité (voir Fig. 10.3), car

Et ().

3. La fonction est définie en un point un et dans un certain voisinage de celui-ci, il y a une limite de la fonction en , mais cette limite n'est pas égale à la valeur de la fonction au point un:

.

Par exemple, la fonction (voir Fig. 10.4)

Voici le point de rupture :

,

Tous les points de discontinuité sont divisés en points de discontinuité amovibles, points de discontinuité du premier et du deuxième type.

Définition 10.1. Le point d'arrêt s'appelle le point espace réparable , si à ce stade il y a des limites finies de la fonction à gauche et à droite, égales entre elles :

.

La limite de la fonction à ce point existe, mais n'est pas égale à la valeur de la fonction au point limite (si la fonction est définie au point limite), ou la fonction au point limite n'est pas définie.

En figue. 10.4 au moment où les conditions de continuité sont violées et la fonction présente une discontinuité. Point sur le graphique (0 ; 1) arraché. Cependant, cet écart peut être facilement éliminé - il suffit de redéfinir cette fonction, en la fixant à ce stade égale à sa limite, c'est-à-dire mettre . Par conséquent, ces espaces sont appelés amovibles.

Définition 10.2. Le point de rupture s’appelle point de discontinuité du 1er type , si à ce stade il y a des limites finies de la fonction à gauche et à droite, mais qu'elles ne sont pas égales entre elles :

.

À ce stade, on dit que la fonction éprouve saut.

En figue. 10.3 la fonction présente une discontinuité de 1ère espèce au point. Les limites gauche et droite à ce stade sont égales :

Et .

Le saut de la fonction au point de discontinuité est égal à .

Il est impossible de définir une telle fonction comme continue. Le graphique est constitué de deux demi-lignes séparées par un saut.

Définition 10.3. Le point de rupture s’appelle point de discontinuité du 2ème type , si au moins une des limites unilatérales de la fonction (gauche ou droite) n'existe pas ou est égale à l'infini.

Sur la figure 10.3, la fonction en un point présente une discontinuité du 2ème type. La fonction considérée at est infiniment grande et n'a de limite finie ni à droite ni à gauche. Il n’est donc pas nécessaire de parler de continuité à ce stade.

Exemple 10.2. Construisez un graphique et déterminez la nature des points de rupture :

Solution. Traçons la fonction F(X) (Figure 10.5).

La figure montre que la fonction d'origine présente trois points de discontinuité : , X 2 = 1,
X 3 = 3. Considérons-les dans l'ordre.

Le point a donc rupture du 2ème type.

a) La fonction est définie à ce stade : F(1) = –1.

b) , ,

ceux. à ce point X 2 = 1 disponible espace réparable. En redéfinissant la valeur de la fonction à ce stade : F(1) = 5, la discontinuité est éliminée et la fonction devient à ce stade continue.

a) La fonction est définie à ce stade : F(3) = 1.

Donc, au point X 1 = 3 disponibles rupture du 1er type. La fonction subit à ce stade un saut égal à D oui= –2–1 = –3.

10.4. Propriétés des fonctions continues

En rappelant les propriétés correspondantes des limites, nous concluons que les fonctions qui sont le résultat d'opérations arithmétiques sur des fonctions continues en un même point sont également continues. Note:

1) si les fonctions et sont continues au point un, alors les fonctions , et (à condition que ) soient également continues à ce stade ;

2) si la fonction est continue au point un et la fonction est continue au point , alors la fonction complexe est continue au point un Et

,

ceux. le signe limite peut être placé sous le signe d'une fonction continue.

Ils disent ça une fonction est continue sur un ensemble si elle est continue en tout point de cet ensemble. Le graphique d’une telle fonction est une ligne continue qui peut être barrée d’un seul trait de stylo.

Tous majeurs les fonctions élémentaires sont continues en tous points où elles sont définies.

Fonctions, continues sur le segment, possèdent un certain nombre de propriétés distinctives importantes. Formulons des théorèmes exprimant certaines de ces propriétés.

Théorème 10.1 (Théorème de Weierstrass ). Si une fonction est continue sur un segment, alors elle atteint ses valeurs minimale et maximale sur ce segment.

Théorème 10.2 (Théorème de Cauchy ). Si une fonction est continue sur un intervalle, alors sur cet intervalle toutes les valeurs intermédiaires entre les plus petites et les plus grandes valeurs.

La propriété importante suivante découle du théorème de Cauchy.

Théorème 10.3. Si une fonction est continue sur un segment et prend des valeurs de signes différents aux extrémités du segment, alors entre a et b il y a un point c auquel la fonction disparaît :.

La signification géométrique de ce théorème est évidente : si le graphique d'une fonction continue va du demi-plan inférieur au demi-plan supérieur (ou vice versa), alors au moins en un point il coupera l'axe Bœuf(Fig. 10.6).

Exemple 10.3. Calculer approximativement la racine de l'équation

, (c'est-à-dire remplacer approximativement) polynôme du degré correspondant.

C'est une propriété très importante des fonctions continues pour la pratique. Par exemple, très souvent les fonctions continues sont spécifiées par des tableaux (données observationnelles ou expérimentales). Ensuite, en utilisant une méthode, vous pouvez remplacer la fonction tabulée par un polynôme. Conformément au théorème 10.3, cela peut toujours être fait avec une précision suffisamment élevée. Travailler avec une fonction définie analytiquement (en particulier un polynôme) est beaucoup plus facile.

10.5. Signification économique de la continuité

La plupart des fonctions utilisées en économie sont continues, ce qui permet de faire des déclarations assez significatives sur le contenu économique.

Pour illustrer, considérons l’exemple suivant.

Taux d'imposition N a à peu près le même graphique que sur la Fig. 10.7a.

Aux extrémités des intervalles elle est discontinue et ces discontinuités sont de la 1ère espèce. Toutefois, le montant de l'impôt sur le revenu lui-même P.(Fig. 10.7b) est une fonction continue du revenu annuel Q. De là, en particulier, il s'ensuit que si les revenus annuels de deux personnes diffèrent de manière insignifiante, alors la différence entre les montants de l'impôt sur le revenu qu'elles doivent payer devrait également différer de manière insignifiante. Il est intéressant de noter que la grande majorité des gens perçoivent cette circonstance comme tout à fait naturelle, à laquelle ils ne pensent même pas.

10.6. Conclusion

Vers la fin, accordons-nous une petite retraite.

Voici comment exprimer graphiquement le triste constat des anciens :

Sic transit Gloria mundi...

(C'est ainsi que passe la gloire terrestre …)

Fin du travail -

Ce sujet appartient à la section :

Notion de fonction

Le concept de fonction.. tout coule et tout change Héraclite.. tableau x x x x y y y y y..

Si vous avez besoin de matériel supplémentaire sur ce sujet, ou si vous n'avez pas trouvé ce que vous cherchiez, nous vous recommandons d'utiliser la recherche dans notre base de données d'œuvres :

Que ferons-nous du matériel reçu :

Si ce matériel vous a été utile, vous pouvez l'enregistrer sur votre page sur les réseaux sociaux :

Définition
Fonction f (X) appelé continu au point x 0 voisinage de ce point, et si la limite lorsque x tend vers x 0 égal à la valeur de la fonction en x 0 :
.

En utilisant les définitions de Cauchy et Heine de la limite d’une fonction, nous pouvons donner définitions élargies de la continuité d'une fonction en un point .

Nous pouvons formuler le concept de continuité dans en termes d'incréments. Pour ce faire, nous introduisons une nouvelle variable, appelée l'incrément de la variable x au point. Alors la fonction est continue au point si
.
Introduisons une nouvelle fonction :
.
Ils l'appellent incrément de fonction au point . Alors la fonction est continue au point si
.

Définition de la continuité à droite (gauche)
Fonction f (X) appelé continue à droite (gauche) au point x 0 , s'il est défini sur un voisinage droit (gauche) de ce point, et si la limite droite (gauche) au point x 0 égal à la valeur de la fonction en x 0 :
.

Théorème sur le caractère limité d'une fonction continue
Soit la fonction f (X) est continue au point x 0 . Alors il y a un quartier U (x0), sur lequel la fonction est limitée.

Théorème sur la préservation du signe d'une fonction continue
Soit la fonction continue au point. Et laissez-le avoir une valeur positive (négative) à ce stade :
.
Il existe alors un voisinage du point où la fonction a une valeur positive (négative) :
à .

Propriétés arithmétiques des fonctions continues
Laissez les fonctions et être continues au point .
Alors les fonctions , et sont continues au point .
Si , alors la fonction est continue au point .

Propriété de continuité gauche-droite
Une fonction est continue en un point si et seulement si elle est continue à droite et à gauche.

Des preuves des propriétés sont données sur la page « Propriétés des fonctions continues en un point ».

Continuité d'une fonction complexe

Théorème de continuité pour une fonction complexe
Soit la fonction continue au point. Et que la fonction soit continue au point.
Alors la fonction complexe est continue en ce point.

Limite d'une fonction complexe

Théorème sur la limite d'une fonction continue d'une fonction
Soit une limite de la fonction en , et elle est égale à :
.
Voici le point t 0 peut être fini ou infiniment distant : .
Et que la fonction soit continue au point.
Alors il existe une limite d’une fonction complexe, et elle est égale à :
.

Théorème sur la limite d'une fonction complexe
Laissez la fonction avoir une limite et mappez un voisinage perforé d'un point sur un voisinage perforé d'un point. Laissez la fonction être définie sur ce quartier et ayez une limite sur celui-ci.
Voici les points finaux ou infiniment éloignés : . Les quartiers et leurs limites correspondantes peuvent être bilatéraux ou unilatéraux.
Alors il existe une limite d’une fonction complexe et elle est égale à :
.

Points de rupture

Détermination du point de rupture
Laissez la fonction être définie sur un voisinage perforé du point. Le point s'appelle point d'arrêt de fonction, si l'une des deux conditions suivantes est remplie :
1) non défini dans ;
2) est défini en , mais ne l'est pas à ce stade.

Détermination du point de discontinuité de 1ère espèce
Le point s'appelle point de discontinuité du premier type, if est un point de rupture et il y a des limites unilatérales finies à gauche et à droite :
.

Définition d'un saut de fonction
Fonction de saut Δ en un point est la différence entre les limites à droite et à gauche
.

Détermination du point de rupture
Le point s'appelle point de rupture amovible, s'il y a une limite
,
mais la fonction en ce point soit n'est pas définie, soit n'est pas égale à la valeur limite : .

Ainsi, le point de discontinuité amovible est le point de discontinuité de 1ère espèce, auquel le saut de la fonction est égal à zéro.

Détermination du point de discontinuité du 2ème type
Le point s'appelle point de discontinuité du deuxième type, s'il ne s'agit pas d'un point de discontinuité de 1ère espèce. Autrement dit, s’il n’y a pas au moins une limite unilatérale, ou au moins une limite unilatérale en un point est égale à l’infini.

Propriétés des fonctions continues sur un intervalle

Définition d'une fonction continue sur un intervalle
Une fonction est dite continue sur un intervalle (at) si elle est continue en tous points de l'intervalle ouvert (at) et aux points a et b, respectivement.

Premier théorème de Weierstrass sur le caractère borné d'une fonction continue sur un intervalle
Si une fonction est continue sur un intervalle, alors elle est bornée sur cet intervalle.

Détermination de la possibilité d'atteindre le maximum (minimum)
Une fonction atteint son maximum (minimum) sur l'ensemble s'il existe un argument pour lequel
pour tous .

Détermination de l'accessibilité de la face supérieure (inférieure)
Une fonction atteint sa limite supérieure (inférieure) sur l'ensemble s'il existe un argument pour lequel
.

Deuxième théorème de Weierstrass sur le maximum et le minimum d'une fonction continue
Une fonction continue sur un segment atteint sur celui-ci ses bornes supérieure et inférieure ou, ce qui revient au même, atteint son maximum et son minimum sur le segment.

Théorème des valeurs intermédiaires de Bolzano-Cauchy
Soit la fonction continue sur le segment. Et soit C un nombre arbitraire situé entre les valeurs de la fonction aux extrémités du segment : et . Il y a alors un point pour lequel
.

Corollaire 1
Soit la fonction continue sur le segment. Et laissez les valeurs de fonction aux extrémités du segment avoir des signes différents : ou . Il y a alors un point auquel la valeur de la fonction est égale à zéro :
.

Corollaire 2
Soit la fonction continue sur le segment. Laisse tomber . Ensuite la fonction prend sur l'intervalle toutes les valeurs de et uniquement ces valeurs :
à .

Fonctions inverses

Définition d'une fonction inverse
Soit une fonction avoir un domaine de définition X et un ensemble de valeurs Y. Et laissez-lui la propriété :
pour tous .
Alors pour tout élément de l’ensemble Y on ne peut associer qu’un seul élément de l’ensemble X auquel . Cette correspondance définit une fonction appelée fonction inverseÀ . La fonction inverse est notée comme suit :
.

De la définition il résulte que
;
pour tous ;
pour tous .

Lemme sur la monotonie mutuelle des fonctions directes et inverses
Si une fonction est strictement croissante (décroissante), alors il existe une fonction inverse qui est également strictement croissante (décroissante).

Propriété de symétrie des graphiques de fonctions directes et inverses
Les graphiques des fonctions directes et inverses sont symétriques par rapport à la droite.

Théorème sur l'existence et la continuité d'une fonction inverse sur un intervalle
Soit la fonction continue et strictement croissante (décroissante) sur le segment. Ensuite, la fonction inverse est définie et continue sur le segment, qui augmente (diminue) strictement.

Pour une fonction croissante. Pour diminuer - .

Théorème sur l'existence et la continuité d'une fonction inverse sur un intervalle
Soit la fonction continue et strictement croissante (décroissante) sur un intervalle ouvert fini ou infini. Ensuite, la fonction inverse est définie et continue sur l'intervalle, qui augmente (diminue) strictement.

Pour une fonction croissante.
Pour diminuer : .

De la même manière, on peut formuler le théorème sur l'existence et la continuité de la fonction inverse sur un demi-intervalle.

Propriétés et continuité des fonctions élémentaires

Les fonctions élémentaires et leurs inverses sont continues dans leur domaine de définition. Ci-dessous, nous présentons les formulations des théorèmes correspondants et fournissons des liens vers leurs preuves.

Fonction exponentielle

Fonction exponentielle f (x) = hache, avec base un > 0 est la limite de la séquence
,
où est une séquence arbitraire de nombres rationnels tendant vers x :
.

Théorème. Propriétés de la fonction exponentielle
La fonction exponentielle a les propriétés suivantes :
(P.0) défini, pour , pour tous ;
(P.1) pour un ≠ 1 a de nombreuses significations ;
(P.2) augmente strictement à , diminue strictement à , est constant à ;
(P.3) ;
(P.3*) ;
(P.4) ;
(P.5) ;
(P.6) ;
(P.7) ;
(P.8) continu pour tous ;
(P.9)à ;
à .

Logarithme

Fonction logarithmique, ou logarithme, y = bûche, avec base un est l'inverse de la fonction exponentielle de base a.

Théorème. Propriétés du logarithme
Fonction logarithmique de base a, y = enregistrer un x, possède les propriétés suivantes :
(L.1) défini et continu, pour et , pour les valeurs positives de l'argument ;
(L.2) a de nombreuses significations ;
(L.3) augmente strictement comme , diminue strictement comme ;
(L.4)à ;
à ;
(L.5) ;
(L.6)à ;
(L.7)à ;
(L.8)à ;
(L.9)à .

Exposant et logarithme népérien

Dans les définitions de la fonction exponentielle et du logarithme, une constante apparaît, appelée base de la puissance ou base du logarithme. En analyse mathématique, dans la grande majorité des cas, des calculs plus simples sont obtenus si le nombre e est utilisé comme base :
.
Une fonction exponentielle de base e est appelée un exposant : , et un logarithme de base e est appelé un logarithme népérien : .

Les propriétés de l'exposant et du logarithme népérien sont présentées sur les pages
"Exposant, e à la puissance x",
"Logarithme népérien, fonction ln x"

Fonction de puissance

Fonction puissance avec exposant p est la fonction f (x) = xp, dont la valeur au point x est égale à la valeur de la fonction exponentielle de base x au point p.
De plus, f (0) = 0 p = 0 pour p > 0 .

Ici, nous considérerons les propriétés de la fonction puissance y = x p pour des valeurs non négatives de l'argument. Pour les rationnels, pour m impair, la fonction puissance est également définie pour x négatif. Dans ce cas, ses propriétés peuvent être obtenues en utilisant des valeurs paires ou impaires.
Ces cas sont discutés en détail et illustrés sur la page « Fonction puissance, ses propriétés et graphiques ».

Théorème. Propriétés de la fonction puissance (x ≥ 0)
Une fonction puissance, y = x p, d'exposant p a les propriétés suivantes :
(C.1) défini et continu sur le plateau
à ,
à ".

Fonctions trigonométriques

Théorème sur la continuité des fonctions trigonométriques
Fonctions trigonométriques : sinus ( péché x), cosinus ( parce que x), tangente ( tgx) et cotangente ( ctg x

Théorème sur la continuité des fonctions trigonométriques inverses
Fonctions trigonométriques inverses : arc sinus ( arc péché x), arc cosinus ( arccos x), arctangente ( arctan x) et l'arc tangent ( arcctg x), sont continus dans leurs domaines de définition.

Les références:
O.I. Bessov. Cours sur l'analyse mathématique. Partie 1. Moscou, 2004.
L.D. Kudryavtsev. Cours d'analyse mathématique. Tome 1. Moscou, 2003.
CM. Nikolski. Cours d'analyse mathématique. Tome 1. Moscou, 1983.

Considérons deux fonctions dont les graphiques sont présentés sur la Fig. 1 et 2. Le graphique de la première fonction peut être dessiné sans retirer le crayon du papier. Cette fonction peut être dite continue. Il est impossible de tracer un graphique d’une autre fonction comme celle-ci. Il se compose de deux pièces continues, et en un point il présente une discontinuité, et nous appellerons la fonction discontinue.

Une telle définition visuelle de la continuité ne peut en aucun cas convenir aux mathématiques, car elle contient des concepts totalement non mathématiques de « crayon » et de « papier ». La définition mathématique exacte de la continuité est donnée sur la base du concept de limite et est la suivante.

Soit une fonction définie sur un segment et soit un point de ce segment. Une fonction est dite continue en un point si, comme elle tend vers (considérée uniquement à partir du segment), les valeurs de la fonction tendent vers, c'est-à-dire Si

. (1)

Une fonction est dite continue sur un segment si elle est continue en chaque point.

Si l'égalité (1) n'est pas satisfaite en un point, la fonction est dite discontinue en ce point.

Comme on le voit, mathématiquement, la propriété de continuité d'une fonction sur un segment est déterminée par la propriété locale de continuité en un point.

La valeur est appelée l'incrément de l'argument, la différence entre les valeurs de la fonction est appelée l'incrément de la fonction et est notée . Évidemment, comme tend l'argument, l'incrément tend vers zéro : .

Réécrivons l'égalité (1) sous la forme équivalente

.

En utilisant la notation introduite, il peut être réécrit comme suit :

Ainsi, si la fonction est continue, alors lorsque l’incrément de l’argument tend vers zéro, l’incrément de la fonction tend vers zéro. On dit aussi d'une autre manière : un petit incrément dans l'argument correspond à un petit incrément dans la fonction. En figue. La figure 3 montre un graphique d'une fonction continue en un point ; l'incrément correspond à l'incrément de la fonction. En figue. 4 incrément correspond à un tel incrément de la fonction qui, aussi petit soit-il, ne sera pas inférieur à la moitié de la longueur du segment ; la fonction est discontinue au point .

Notre idée d'une fonction continue en tant que fonction dont le graphique peut être dessiné sans lever le crayon du papier est parfaitement confirmée par les propriétés des fonctions continues, prouvées en analyse mathématique. Notons, par exemple, de telles propriétés.

1. Si une fonction continue sur un segment prend des valeurs de signes différents aux extrémités du segment, alors à un moment donné de ce segment, elle prend une valeur égale à zéro.

2. Une fonction continue sur le segment prend toutes les valeurs intermédiaires entre les valeurs aux points terminaux, c'est-à-dire Entre et .

3. Si une fonction est continue sur un segment, alors sur ce segment elle atteint sa valeur maximale et sa valeur minimale, c'est-à-dire si est la plus petite et a est la plus grande valeur de la fonction sur le segment , alors sur ce segment il y a des points et tels que et .

La signification géométrique de la première de ces affirmations est tout à fait claire : si une courbe continue passe d'un côté à l'autre d'un axe, alors elle coupe cet axe (Fig. 5). Une fonction discontinue n'a pas cette propriété, ce qui est confirmé par le graphique de la fonction de la Fig. 2, ainsi que les propriétés 2 et 3. Sur la Fig. La fonction 2 ne prend pas de valeur, même si elle est comprise entre et. En figue. La figure 6 montre un exemple de fonction discontinue (partie fractionnaire d'un nombre) qui n'atteint pas sa plus grande valeur.

L'addition, la soustraction, la multiplication de fonctions continues sur le même segment conduisent à nouveau à des fonctions continues. Lors de la division de deux fonctions continues, le résultat est une fonction continue si le dénominateur est partout différent de zéro.

Les mathématiques sont parvenues au concept de fonction continue en étudiant tout d’abord diverses lois du mouvement. L'espace et le temps sont continus, et la dépendance, par exemple, d'un chemin au temps, exprimée par une loi, fournit un exemple de fonction continue.

Les fonctions continues sont utilisées pour décrire les états et les processus dans les solides, les liquides et les gaz. Les sciences qui les étudient - la théorie de l'élasticité, de l'hydrodynamique et de l'aérodynamique - sont réunies sous un seul nom - « mécanique des continus ».

Dans cette leçon, nous apprendrons comment établir la continuité d'une fonction. Nous le ferons en utilisant des limites, unilatérales en plus - droite et gauche, qui ne font pas du tout peur, malgré le fait qu'elles s'écrivent comme et .

Mais qu’est-ce que la continuité d’une fonction ? En attendant d'arriver à une définition stricte, il est plus facile d'imaginer une ligne qui peut être tracée sans retirer le crayon du papier. Si une telle ligne est tracée, alors elle est continue. Cette droite est le graphique d’une fonction continue.

Graphiquement, une fonction est continue en un point si son graphique ne se « casse » pas en ce point. Le graphique d’une telle fonction continue est illustré dans la figure ci-dessous.

Détermination de la continuité d'une fonction à travers une limite. Une fonction est continue en un point si trois conditions sont remplies :

1. La fonction est définie au point .

Si au moins une des conditions énumérées n’est pas remplie, la fonction n’est pas continue à ce stade. Dans ce cas, ils disent que la fonction souffre d'une discontinuité, et les points du graphique où le graphique est interrompu sont appelés points de discontinuité de la fonction. Le graphique d'une telle fonction qui subit une discontinuité au point x=2 est dans la figure ci-dessous.

Exemple 1. Fonction F(X) est défini comme suit :

Cette fonction sera-t-elle continue à chacun des points limites de ses branches, c'est-à-dire aux points X = 0 , X = 1 , X = 3 ?

Solution. Nous vérifions les trois conditions pour la continuité d'une fonction à chaque point limite. La première condition est remplie, puisque quoi fonction définieà chacun des points limites découle de la définition de la fonction. Reste à vérifier les deux conditions restantes.

Point X= 0 . Trouvons la limite de gauche à ce stade :

.

Trouvons la limite de droite :

X= 0 doit être trouvé pour la branche de la fonction qui inclut ce point, c'est-à-dire la deuxième branche. On les retrouve :

Comme on peut le voir, la limite de la fonction et la valeur de la fonction au point X= 0 sont égaux. La fonction est donc continue au point X = 0 .

Point X= 1 . Trouvons la limite de gauche à ce stade :

Trouvons la limite de droite :

Limite d'une fonction et valeur d'une fonction en un point X= 1 doit être trouvé pour la branche de la fonction qui inclut ce point, c'est-à-dire la deuxième branche. On les retrouve :

.

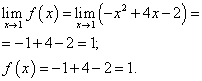Limite d'une fonction et valeur d'une fonction en un point X= 1 sont égaux. La fonction est donc continue au point X = 1 .

Point X= 3 . Trouvons la limite de gauche à ce stade :

Trouvons la limite de droite :

Limite d'une fonction et valeur d'une fonction en un point X= 3 doit être trouvé pour la branche de la fonction qui inclut ce point, c'est-à-dire la deuxième branche. On les retrouve :

.

Limite d'une fonction et valeur d'une fonction en un point X= 3 sont égaux. La fonction est donc continue au point X = 3 .

La conclusion principale : cette fonction est continue en chaque point frontière.

Établissez vous-même la continuité d'une fonction en un point, puis regardez la solution

Un changement continu dans une fonction peut être défini comme un changement progressif, sans sauts, dans lequel un petit changement dans l'argument entraîne un petit changement dans la fonction.

Illustrons ce changement continu de fonction par un exemple.

Laissez un poids pendre à un fil au-dessus de la table. Sous l'influence de cette charge, le fil s'étire, donc la distance je la charge à partir du point de suspension du fil est fonction de la masse de la charge m, c'est je = F(m) , m≥0 .

Si vous modifiez légèrement la masse de la charge, alors la distance je changera peu : petits changements m de petits changements correspondent je. Cependant, si la masse de la charge est proche de la résistance à la traction du filetage, alors une légère augmentation de la masse de la charge peut provoquer la rupture du filetage : distance je augmentera brusquement et deviendra égale à la distance entre le point de suspension et la surface de la table. Graphique d'une fonction je = F(m) montré sur la figure. Au niveau d'une section, ce graphique est une ligne continue (solide) et à un moment donné, il est interrompu. Le résultat est un graphe composé de deux branches. En tout point sauf , la fonction je = F(m) est continu, mais en un point il présente une discontinuité.

L'étude de la continuité d'une fonction peut être soit une tâche indépendante, soit l'une des étapes d'une étude complète de la fonction et de la construction de son graphique.

Continuité d'une fonction sur un intervalle

Laissez la fonction oui = F(X) défini dans l'intervalle ] un, b[ et est continue en tout point de cet intervalle. Alors on l'appelle continu dans l'intervalle ] un, b[ . La notion de continuité d'une fonction sur des intervalles de la forme ]- ∞ se définit de la même manière, b[ , ]un, + ∞[ , ]- ∞, + ∞[ . Laissez maintenant la fonction oui = F(X) défini sur l'intervalle [ un, b] . La différence entre un intervalle et un segment : les points limites d'un intervalle ne sont pas inclus dans l'intervalle, mais les points limites d'un segment sont inclus dans le segment. Il convient ici de mentionner ce qu'on appelle la continuité unilatérale : au point un, restant sur le segment [ un, b] , on ne peut approcher que par la droite, et au point b- seulement à gauche. La fonction est dite continue sur l’intervalle [ un, b] , s'il est continu en tous les points intérieurs de ce segment, continu à droite au point un et reste continu au point b.

Un exemple de fonction continue peut être n'importe laquelle des fonctions élémentaires. Chaque fonction élémentaire est continue sur tout intervalle sur lequel elle est définie. Par exemple, les fonctions et sont continues sur n'importe quel intervalle [ un, b], la fonction est continue sur l'intervalle [ 0 , b] , la fonction est continue sur tout segment ne contenant pas de point un = 2 .

Exemple 4. Examinez la continuité de la fonction.

Solution. Vérifions la première condition. La fonction n'est pas définie aux points - 3 et 3. Au moins une des conditions de continuité de la fonction sur toute la droite numérique n'est pas remplie. Cette fonction est donc continue sur les intervalles

Exemple 5. Déterminer à quelle valeur du paramètre un continu tout au long domaine de définition fonction

Solution.

Trouvons la limite de droite à :

.

Évidemment, la valeur au point X= 2 devrait être égal hache :

un = 1,5 .

Exemple 6. Déterminer à quelles valeurs de paramètre un Et b continu tout au long domaine de définition fonction

Solution.
Trouvons la limite gauche de la fonction au point :

.

Par conséquent, la valeur au point doit être 1 :

Trouvons la fonction de gauche au point :

Évidemment, la valeur de la fonction en un point doit être égale à :

Réponse : la fonction est continue sur tout le domaine de définition lorsque un = 1; b = -3 .

Propriétés de base des fonctions continues

Les mathématiques sont parvenues au concept de fonction continue en étudiant tout d’abord diverses lois du mouvement. L'espace et le temps sont infinis, et la dépendance, par exemple, des chemins s de temps t, exprimé par la loi s = F(t) , donne un exemple d'un continu les fonctions F(t) . La température de l’eau chauffée change également de façon continue ; c’est aussi une fonction continue du temps : T = F(t) .

En analyse mathématique, certaines propriétés des fonctions continues sont prouvées. Présentons la plus importante de ces propriétés.

1. Si une fonction continue sur un intervalle prend des valeurs de signes différents aux extrémités de l'intervalle, alors à un moment donné de cet intervalle, elle prend une valeur égale à zéro. De manière plus formelle, cette propriété est donnée dans un théorème connu sous le nom de premier théorème de Bolzano-Cauchy.

2. Fonction F(X) , continue sur l'intervalle [ un, b] , prend toutes les valeurs intermédiaires entre les valeurs aux points finaux, c'est-à-dire entre F(un) Et F(b) . Dans une formulation plus formelle, cette propriété est donnée dans un théorème connu sous le nom de deuxième théorème de Bolzano-Cauchy.