Намерете условния екстремум и екстремните стойности. Условен екстремум

Пример

Намерете екстремума на функцията при условие, че хИ приса свързани с отношението: . Геометрично задачата означава следното: върху елипса
самолет
.

Този проблем може да се реши по този начин: от уравнението
намираме
х:

при условие че
, сведен до проблема за намиране на екстремума на функция на една променлива в интервала
.

Геометрично задачата означава следното: върху елипса , получен чрез пресичане на цилиндъра
самолет
, трябва да намерите максималната или минималната стойност на приложението (фиг.9). Този проблем може да се реши по този начин: от уравнението
намираме
. Замествайки намерената стойност на y в уравнението на равнината, получаваме функция на една променлива х:

По този начин проблемът за намиране на екстремума на функцията
при условие че
, сведен до проблема за намиране на екстремума на функция на една променлива на интервал.

Така, проблемът за намиране на условен екстремум– това е задачата за намиране на екстремума на целевата функция
, при условие че променливите хИ припредмет на ограничение
, Наречен уравнение на връзката.

Да кажем това точка
, удовлетворяващ уравнението за свързване, е точката на локалния условен максимум (минимум), ако има квартал
така че за всякакви точки
, чиито координати удовлетворяват уравнението на връзката, неравенството е изпълнено.

Ако от уравнението на свързване може да се намери израз за при, след това чрез заместване на този израз в оригиналната функция, ние превръщаме последната в сложна функция на една променлива Х.

Общият метод за решаване на проблема с условния екстремум е Метод на умножителя на Лагранж. Нека създадем спомагателна функция, където ─ някакво число. Тази функция се нарича Функция на Лагранж, А ─ Множител на Лагранж. По този начин задачата за намиране на условен екстремум е сведена до намиране на локални точки на екстремум за функцията на Лагранж. За да намерите възможни точки на екстремум, трябва да решите система от 3 уравнения с три неизвестни x, yИ.

Тогава трябва да използвате следното достатъчно условие за екстремум.

ТЕОРЕМА. Нека точката е възможна точка на екстремум за функцията на Лагранж. Да приемем, че в околността на точката
има непрекъснати частни производни от втория ред на функциите И . Нека обозначим

Тогава ако
, Че
─ условна точка на екстремум на функцията
с уравнението на свързване
в този случай, ако
, Че
─ условна минимална точка, ако
, Че
─ условна максимална точка.

§8. Градиент и производна на посоката

Нека функцията
определени в някакъв (отворен) регион. Помислете за всяка точка
тази област и всяка насочена права линия (ос) , минаваща през тази точка (фиг. 1). Позволявам
- някаква друга точка на тази ос,
– дължина на отсечката между
И
, взети със знак плюс, ако посоката
съвпада с посоката на оста , и със знак минус, ако посоките им са противоположни.

Позволявам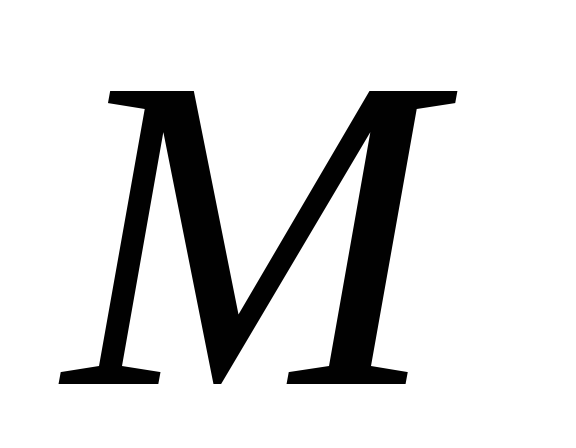
подходи за неопределено време
. Лимит

Наречен производна на функция
към (или по оста ) и се означава по следния начин:

.

Тази производна характеризира "скоростта на промяна" на функцията в точката
към . По-специално обикновените частни производни ,могат също да се разглеждат като производни "по отношение на посоката".

Нека сега приемем, че функцията
има непрекъснати частични производни в разглеждания регион. Нека оста образува ъгли с координатните оси
И . При направените предположения производната по посока съществува и се изразява с формулата

.

Ако векторът
даден от неговите координати
, след това производната на функцията
по посока на вектора
може да се изчисли по формулата:

.

Вектор с координати
Наречен градиентен векторфункции
в точката
. Градиентният вектор показва посоката на най-бързото нарастване на функцията в дадена точка.

Пример

Дадена е функция, точка A(1, 1) и вектор
. Намерете: 1)grad z в точка A; 2) производна в точка А по посока на вектора .

Частни производни на дадена функция в точка
:

;
.

Тогава градиентният вектор на функцията в тази точка е:
. Градиентният вектор може също да бъде написан чрез векторно разлагане И :

. Производна на функция по посока на вектора :

Така,
,
.◄

Условен екстремум.

Екстремуми на функция на няколко променливи

Метод на най-малките квадрати.

Локален екстремум на FNP

Нека функцията е дадена И= f(P), РÎDÌR ни нека точка P 0 ( А 1 , А 2 , ..., a p) –вътрешниточка на множество D.

Определение 9.4.

1) Точка P 0 се нарича максимална точка функции И= f(P), ако съществува околност на тази точка U(P 0) М D такава, че за всяка точка P( х 1 , х 2 , ..., x n)О U(P 0) , Р¹Р 0 , условието е изпълнено f(P)£ f(P 0) . Значение f(P 0) се извиква функция в максималната точка максимум на функцията и е обозначен f(P0) = макс f(P) .

2) Точка P 0 се нарича минимална точка функции И= f(P), ако има околност на тази точка U(P 0)Ì D такава, че за всяка точка P( х 1 , х 2 , ..., x n)ОU(P 0), Р¹Р 0 , условието е изпълнено f(P)³ f(P 0) . Значение f(P 0) се извиква функция в минималната точка минимална функция и е обозначен f(P 0) = мин f(P).

Точките на минимум и максимум на функция се наричат екстремни точки, стойностите на функцията в екстремните точки се наричат екстремуми на функцията.

Както следва от определението, неравенствата f(P)£ f(P 0) , f(P)³ f(P 0) трябва да бъде изпълнено само в определена околност на точката P 0, а не в цялата област на дефиниране на функцията, което означава, че функцията може да има няколко екстремума от същия тип (няколко минимума, няколко максимума) . Следователно дефинираните по-горе екстремуми се наричат местен(локални) крайности.

Теорема 9.1 (необходимо условие за екстремума на FNP)

Ако функцията И= f(х 1 , х 2 , ..., x n) има екстремум в точката P 0 , тогава неговите частни производни от първи ред в тази точка са или равни на нула, или не съществуват.

Доказателство.Нека в точка P 0 ( А 1 , А 2 , ..., a p) функция И= f(P) има екстремум, например максимум. Нека оправим аргументите х 2 , ..., x n, поставяне х 2 =А 2 ,..., x n = a p. Тогава И= f(P) = f 1 ((х 1 , А 2 , ..., a p) е функция на една променлива х 1 . Тъй като тази функция има х 1 = А 1 екстремум (максимум), тогава f 1 ¢=0 или не съществува, когато х 1 =А 1 (необходимо условие за съществуването на екстремум на функция на една променлива). Но това означава или не съществува в точка P 0 - екстремалната точка. По подобен начин можем да разгледаме частични производни по отношение на други променливи. CTD.

Точките в областта на функция, в които частни производни от първи ред са равни на нула или не съществуват, се наричат критични точки тази функция.

Както следва от теорема 9.1, екстремалните точки на FNP трябва да се търсят сред критичните точки на функцията. Но що се отнася до функция на една променлива, не всяка критична точка е точка на екстремум.

Теорема 9.2 (достатъчно условие за екстремума на FNP)

Нека P 0 е критичната точка на функцията И= f(P) и е диференциал от втори ред на тази функция. Тогава

и ако д 2 u(P 0) > 0 при , тогава P 0 е точка минимумфункции И= f(P);

б) ако д 2 u(P0)< 0 при , то Р 0 – точка максимумфункции И= f(P);

в) ако д 2 u(P 0) не е дефиниран със знак, тогава P 0 не е точка на екстремум;

Ще разгледаме тази теорема без доказателство.

Имайте предвид, че теоремата не разглежда случая, когато д 2 u(P 0) = 0 или не съществува. Това означава, че въпросът за наличието на екстремум в точката P 0 при такива условия остава отворен - необходими са допълнителни изследвания, например изследване на увеличението на функцията в тази точка.

В по-подробни курсове по математика е доказано, че по-специално за функцията z = f(х,г) на две променливи, чийто диференциал от втори ред е сбор от формата

изследването на наличието на екстремум в критичната точка P 0 може да бъде опростено.

Нека означим , , . Да съставим детерминанта

.

Оказа се:

д 2 z> 0 в точка P 0, т.е. P 0 – минимална точка, ако А(P 0) > 0 и D(P 0) > 0;

д 2 z < 0 в точке Р 0 , т.е. Р 0 – точка максимума, если А(P0)< 0 , а D(Р 0) > 0;

ако D(P 0)< 0, то д 2 zв близост до точка P 0 променя знака и в точка P 0 няма екстремум;

ако D(Р 0) = 0, тогава са необходими допълнителни изследвания на функцията в близост до критичната точка Р 0.

По този начин, за функцията z = f(х,г) от две променливи имаме следния алгоритъм (нека го наречем „алгоритъм D“) за намиране на екстремум:

1) Намерете областта на дефиницията D( f) функции.

2) Намерете критични точки, т.е. точки от D( f), за които и са равни на нула или не съществуват.

3) Във всяка критична точка P 0 проверете достатъчните условия за екстремума. За да направите това, намерете , където , , и изчислява D(P 0) и А(P 0). Тогава:

ако D(P 0) >0, тогава в точка P 0 има екстремум и ако А(P 0) > 0 – тогава това е минимумът и ако А(P 0)< 0 – максимум;

ако D(P 0)< 0, то в точке Р­ 0 нет экстремума;

Ако D(P 0) = 0, тогава са необходими допълнителни изследвания.

4) В намерените точки на екстремум изчислете стойността на функцията.

Пример 1.

Намерете екстремума на функцията z = х 3 + 8г 3 – 3xy .

Решение.Областта на дефиниране на тази функция е цялата координатна равнина. Да намерим критичните точки.

, , Þ P 0 (0,0) , .

Нека проверим дали са изпълнени достатъчните условия за екстремума. Ще намерим

6х, = -3, = 48приИ = 288xy – 9.

Тогава D(P 0) = 288×0×0 – 9 = -9< 0 , значит, в точке Р 0 экстремума нет.

D(Р 1) = 36-9>0 – в точка Р 1 има екстремум, а тъй като А(P 1) = 3 >0, тогава този екстремум е минимум. Значи мин z=z(P 1) = .

Пример 2.

Намерете екстремума на функцията .

Решение: D( f) =R 2 . Критични точки: ; не съществува кога при= 0, което означава, че P 0 (0,0) е критичната точка на тази функция.

2, = 0, = , = , но D(P 0) не е дефиниран, така че изучаването на неговия знак е невъзможно.

По същата причина е невъзможно теорема 9.2 да се приложи директно - д 2 zне съществува в този момент.

Нека разгледаме нарастването на функцията f(х, г) в точка P 0 . Ако Д f =f(P) – f(P 0)>0 "P, тогава P 0 е минималната точка, но ако D f < 0, то Р 0 – точка максимума.

В нашия случай имаме

д f = f(х, г) – f(0, 0) = f(0+D х,0+D г) – f(0, 0) = .

В Д х= 0,1 и D г= -0,008 получаваме D f = 0,01 – 0,2 < 0, а при Dх= 0,1 и D г= 0,001 D f= 0,01 + 0,1 > 0, т.е. в близост до точка P 0 нито едно условие D не е изпълнено f <0 (т.е. f(х, г) < f(0, 0) и следователно P 0 не е максимална точка), нито условие D f>0 (т.е. f(х, г) > f(0, 0) и тогава P 0 не е минимална точка). Това означава, че по дефиниция на екстремум тази функция няма екстремуми.

Условен екстремум.

Разглежданият екстремум на функцията се нарича безусловен, тъй като не се налагат ограничения (условия) върху аргументите на функцията.

Определение 9.2.Екстремум на функцията И = f(х 1 , х 2 , ... , x n), намерени при условие, че неговите аргументи х 1 , х 2 , ... , x nудовлетворяват уравненията j 1 ( х 1 , х 2 , ... , x n) = 0, …, j T(х 1 , х 2 , ... , x n) = 0, където P ( х 1 , х 2 , ... , x n) О D( f), Наречен условен екстремум .

Уравнения j к(х 1 , х 2 , ... , x n) = 0 , к = 1, 2,..., м, са наречени уравнения на връзката.

Нека да разгледаме функциите z = f(х,г) две променливи. Ако уравнението на връзката е едно, т.е. , тогава намирането на условен екстремум означава, че екстремумът се търси не в цялата област на дефиниране на функцията, а върху някаква крива, лежаща в D( f) (т.е. не е най-високият или най-високият ниски точкиповърхности z = f(х,г), и най-високите или най-ниските точки сред точките на пресичане на тази повърхност с цилиндъра, фиг. 5).

Условен екстремум на функция z = f(х,г) от две променливи може да се намери по следния начин( метод на елиминиране). От уравнението изразете една от променливите като функция на друга (например напишете ) и, замествайки тази стойност на променливата във функцията, напишете последната като функция на една променлива (в разглеждания случай ). Намерете екстремума на получената функция на една променлива.

Първо, нека разгледаме случая на функция на две променливи. Условният екстремум на функция $z=f(x,y)$ в точка $M_0(x_0;y_0)$ е екстремумът на тази функция, постигнат при условие, че променливите $x$ и $y$ в околностите на тази точка отговарят на уравнението за връзка $\ varphi (x,y)=0$.

Името „условен“ екстремум се дължи на факта, че върху променливите е наложено допълнително условие $\varphi(x,y)=0$. Ако една променлива може да бъде изразена от уравнението на връзката чрез друга, тогава проблемът за определяне на условния екстремум се свежда до проблема за определяне на обичайния екстремум на функция на една променлива. Например, ако уравнението на връзката предполага $y=\psi(x)$, тогава замествайки $y=\psi(x)$ в $z=f(x,y)$, получаваме функция на една променлива $z =f\left (x,\psi(x)\right)$. В общия случай обаче този метод е малко полезен, така че се налага въвеждането на нов алгоритъм.

Метод на умножителя на Лагранж за функции на две променливи.

Методът на умножителя на Лагранж се състои от конструиране на функция на Лагранж за намиране на условен екстремум: $F(x,y)=f(x,y)+\lambda\varphi(x,y)$ (параметърът $\lambda$ се нарича множител на Лагранж). Необходимите условия за екстремума се определят от система от уравнения, от които се определят стационарните точки:

$$ \left \( \begin(aligned) & \frac(\partial F)(\partial x)=0;\\ & \frac(\partial F)(\partial y)=0;\\ & \varphi (x,y)=0. \end(aligned) \right. $$

Достатъчно условие, от което може да се определи естеството на екстремума, е знакът $d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy) ^("" )dy^2$. Ако в стационарна точка $d^2F > 0$, тогава функцията $z=f(x,y)$ има условен минимум в тази точка, но ако $d^2F< 0$, то условный максимум.

Има и друг начин да се определи естеството на екстремума. От уравнението на свързване получаваме: $\varphi_(x)^(")dx+\varphi_(y)^(")dy=0$, $dy=-\frac(\varphi_(x)^("))( \varphi_ (y)^("))dx$, следователно във всяка неподвижна точка имаме:

$$d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=F_(xx)^( "")dx^2+2F_(xy)^("")dx\left(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\right)+ F_(yy)^("")\left(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\right)^2=\\ =-\frac (dx^2)(\left(\varphi_(y)^(") \right)^2)\cdot\left(-(\varphi_(y)^("))^2 F_(xx)^(" ")+2\varphi_(x)^(")\varphi_(y)^(")F_(xy)^("")-(\varphi_(x)^("))^2 F_(yy)^ ("") \вдясно)$$

Вторият фактор (разположен в скоби) може да бъде представен в следната форма:

Елементите на детерминантата $\left| са маркирани в червено. \begin(масив) (cc) F_(xx)^("") & F_(xy)^("") \\ F_(xy)^("") & F_(yy)^("") \end (масив)\right|$, което е хесианът на функцията на Лагранж. Ако $H > 0$, тогава $d^2F< 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F >0$, т.е. имаме условен минимум на функцията $z=f(x,y)$.

Бележка относно записа на детерминанта $H$. Покажи скрий

$$ H=-\left|\begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_ (xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \ край (масив) \right| $$

В тази ситуация правилото, формулирано по-горе, ще се промени, както следва: ако $H > 0$, тогава функцията има условен минимум и ако $H< 0$ получим условный максимум функции $z=f(x,y)$. При решении задач следует учитывать такие нюансы.

Алгоритъм за изследване на функция на две променливи за условен екстремум

1. Съставете функцията на Лагранж $F(x,y)=f(x,y)+\lambda\varphi(x,y)$
2. Решете системата $ \left \( \begin(aligned) & \frac(\partial F)(\partial x)=0;\\ & \frac(\partial F)(\partial y)=0;\\ & \ varphi (x,y)=0. \end(aligned) \right.$
3. Определете естеството на екстремума във всяка от стационарните точки, намерени в предходния параграф. За да направите това, използвайте някой от следните методи:
   • Съставете детерминантата на $H$ и намерете знака му
   • Като вземете предвид уравнението за свързване, изчислете знака на $d^2F$

Метод на множителя на Лагранж за функции на n променливи

Да кажем, че имаме функция от $n$ променливи $z=f(x_1,x_2,\ldots,x_n)$ и $m$ уравнения за свързване ($n > m$):

$$\varphi_1(x_1,x_2,\ldots,x_n)=0; \; \varphi_2(x_1,x_2,\ldots,x_n)=0,\ldots,\varphi_m(x_1,x_2,\ldots,x_n)=0.$$

Означавайки множителите на Лагранж като $\lambda_1,\lambda_2,\ldots,\lambda_m$, съставяме функцията на Лагранж:

$$F(x_1,x_2,\ldots,x_n,\lambda_1,\lambda_2,\ldots,\lambda_m)=f+\lambda_1\varphi_1+\lambda_2\varphi_2+\ldots+\lambda_m\varphi_m$$

Необходимите условия за наличие на условен екстремум се дават от система от уравнения, от които се намират координатите на стационарни точки и стойностите на множителите на Лагранж:

$$\left\(\begin(aligned) & \frac(\partial F)(\partial x_i)=0; (i=\overline(1,n))\\ & \varphi_j=0; (j=\ overline(1,m)) \end(aligned) \right.$$

Можете да разберете дали функцията има условен минимум или условен максимум в намерената точка, както преди, като използвате знака $d^2F$. Ако в намерената точка $d^2F > 0$, тогава функцията има условен минимум, но ако $d^2F< 0$, - то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:

Детерминанта на матрицата $\left| \begin(масив) (ccccc) \frac(\partial^2F)(\partial x_(1)^(2)) & \frac(\partial^2F)(\partial x_(1)\partial x_(2) ) & \frac(\partial^2F)(\partial x_(1)\partial x_(3)) &\ldots & \frac(\partial^2F)(\partial x_(1)\partial x_(n)) \\ \frac(\partial^2F)(\partial x_(2)\partial x_1) & \frac(\partial^2F)(\partial x_(2)^(2)) & \frac(\partial^2F )(\partial x_(2)\partial x_(3)) &\ldots & \frac(\partial^2F)(\partial x_(2)\partial x_(n))\\ \frac(\partial^2F )(\partial x_(3) \partial x_(1)) & \frac(\partial^2F)(\partial x_(3)\partial x_(2)) & \frac(\partial^2F)(\partial x_(3)^(2)) &\ldots & \frac(\partial^2F)(\partial x_(3)\partial x_(n))\\ \ldots & \ldots & \ldots &\ldots & \ ldots\\ \frac(\partial^2F)(\partial x_(n)\partial x_(1)) & \frac(\partial^2F)(\partial x_(n)\partial x_(2)) & \ frac(\partial^2F)(\partial x_(n)\partial x_(3)) &\ldots & \frac(\partial^2F)(\partial x_(n)^(2))\\ \end( масив) \right|$, подчертано в червено в матрицата $L$, е Хесианът на функцията на Лагранж. Използваме следното правило:

• Ако знаците на ъгловите минори $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ матрици $L$ съвпадат със знака на $(-1)^m$, тогава изследваната стационарна точка е условната минимална точка на функцията $ z=f(x_1,x_2 ,x_3,\ldots,x_n)$.
• Ако знаците на ъгловите минори $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ се редуват и знакът на второстепенното $H_(2m+1)$ съвпада със знака на числото $(-1)^(m+1 )$, тогава стационарната точка е условната максимална точка на функцията $z=f(x_1,x_2,x_3,\ldots,x_n)$.

Пример №1

Намерете условния екстремум на функцията $z(x,y)=x+3y$ при условие $x^2+y^2=10$.

Геометричната интерпретация на тази задача е следната: изисква се да се намерят най-голямата и най-малката стойност на апликацията на равнината $z=x+3y$ за точките на нейното пресичане с цилиндъра $x^2+y ^2=10$.

Донякъде е трудно да изразим една променлива чрез друга от уравнението за свързване и да я заместим във функцията $z(x,y)=x+3y$, така че ще използваме метода на Лагранж.

Означавайки $\varphi(x,y)=x^2+y^2-10$, съставяме функцията на Лагранж:

$$ F(x,y)=z(x,y)+\lambda \varphi(x,y)=x+3y+\lambda(x^2+y^2-10);\\ \frac(\partial F)(\partial x)=1+2\lambda x; \frac(\partial F)(\partial y)=3+2\lambda y. $$

Нека напишем система от уравнения за определяне на стационарните точки на функцията на Лагранж:

$$ \left \( \begin(aligned) & 1+2\lambda x=0;\\ & 3+2\lambda y=0;\\ & x^2+y^2-10=0. \end (подравнено)\вдясно.$$

Ако приемем $\lambda=0$, тогава първото уравнение става: $1=0$. Полученото противоречие показва, че $\lambda\neq 0$. При условието $\lambda\neq 0$, от първото и второто уравнение имаме: $x=-\frac(1)(2\lambda)$, $y=-\frac(3)(2\lambda) $. Замествайки получените стойности в третото уравнение, получаваме:

$$ \left(-\frac(1)(2\lambda) \right)^2+\left(-\frac(3)(2\lambda) \right)^2-10=0;\\ \frac (1)(4\lambda^2)+\frac(9)(4\lambda^2)=10; \lambda^2=\frac(1)(4); \left[ \begin(aligned) & \lambda_1=-\frac(1)(2);\\ & \lambda_2=\frac(1)(2). \end(aligned) \right.\\ \begin(aligned) & \lambda_1=-\frac(1)(2); \; x_1=-\frac(1)(2\lambda_1)=1; \; y_1=-\frac(3)(2\lambda_1)=3;\\ & \lambda_2=\frac(1)(2); \; x_2=-\frac(1)(2\lambda_2)=-1; \; y_2=-\frac(3)(2\lambda_2)=-3.\край (подравнено) $$

И така, системата има две решения: $x_1=1;\; y_1=3;\; \lambda_1=-\frac(1)(2)$ и $x_2=-1;\; y_2=-3;\; \lambda_2=\frac(1)(2)$. Нека разберем природата на екстремума във всяка стационарна точка: $M_1(1;3)$ и $M_2(-1;-3)$. За да направим това, ние изчисляваме детерминантата на $H$ във всяка точка.

$$ \varphi_(x)^(")=2x;\; \varphi_(y)^(")=2y;\; F_(xx)^("")=2\ламбда;\; F_(xy)^("")=0;\; F_(yy)^("")=2\lambda.\\ H=\left| \begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \end(array) \right|= \ляво| \begin(масив) (ccc) 0 & 2x & 2y\\ 2x & 2\lambda & 0 \\ 2y & 0 & 2\lambda \end(масив) \right|= 8\cdot\left| \begin(масив) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(масив) \right| $$

В точка $M_1(1;3)$ получаваме: $H=8\cdot\left| \begin(масив) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(масив) \right|= 8\cdot\left| \begin(array) (ccc) 0 & 1 & 3\\ 1 & -1/2 & 0 \\ 3 & 0 & -1/2 \end(array) \right|=40 > 0$, така че при точка $M_1(1;3)$ функцията $z(x,y)=x+3y$ има условен максимум, $z_(\max)=z(1;3)=10$.

По същия начин в точка $M_2(-1,-3)$ намираме: $H=8\cdot\left| \begin(масив) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(масив) \right|= 8\cdot\left| \begin(array) (ccc) 0 & -1 & -3\\ -1 & 1/2 & 0 \\ -3 & 0 & 1/2 \end(array) \right|=-40$. От $H< 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{\min}=z(-1;-3)=-10$.

Отбелязвам, че вместо да се изчислява стойността на детерминантата $H$ във всяка точка, е много по-удобно да се разшири в общ изглед. За да не претрупвам текста с подробности, ще скрия този метод под бележка.

Записване на детерминантата $H$ в общ вид. Покажи скрий

$$ H=8\cdot\left|\begin(array)(ccc)0&x&y\\x&\lambda&0\\y&0&\lambda\end(array)\right| =8\cdot\left(-\lambda(y^2)-\lambda(x^2)\right) =-8\lambda\cdot\left(y^2+x^2\right). $$

По принцип вече е очевидно какъв знак има $H$. Тъй като нито една от точките $M_1$ или $M_2$ не съвпада с началото, то $y^2+x^2>0$. Следователно знакът на $H$ е противоположен на знака на $\lambda$. Можете да завършите изчисленията:

$$ \begin(aligned) &H(M_1)=-8\cdot\left(-\frac(1)(2)\right)\cdot\left(3^2+1^2\right)=40;\ \ &H(M_2)=-8\cdot\frac(1)(2)\cdot\left((-3)^2+(-1)^2\right)=-40. \end(подравнено) $$

Въпросът за природата на екстремума в стационарните точки $M_1(1;3)$ и $M_2(-1;-3)$ може да бъде решен без използване на детерминантата $H$. Нека намерим знака на $d^2F$ във всяка неподвижна точка:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=2\lambda \left( dx^2+dy^2\right) $$

Нека отбележа, че записът $dx^2$ означава точно $dx$, повдигнат на втора степен, т.е. $\left(dx \right)^2$. Следователно имаме: $dx^2+dy^2>0$, следователно с $\lambda_1=-\frac(1)(2)$ получаваме $d^2F< 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.

Отговор: в точка $(-1;-3)$ функцията има условен минимум, $z_(\min)=-10$. В точка $(1;3)$ функцията има условен максимум, $z_(\max)=10$

Пример №2

Намерете условния екстремум на функцията $z(x,y)=3y^3+4x^2-xy$ при условие $x+y=0$.

Първи метод (метод на умножителя на Лагранж)

Означавайки $\varphi(x,y)=x+y$, съставяме функцията на Лагранж: $F(x,y)=z(x,y)+\lambda \varphi(x,y)=3y^3+ 4x^2 -xy+\lambda(x+y)$.

$$ \frac(\partial F)(\partial x)=8x-y+\lambda; \; \frac(\partial F)(\partial y)=9y^2-x+\lambda.\\ \left \( \begin(aligned) & 8x-y+\lambda=0;\\ & 9y^2-x+\ ламбда=0; \\ & x+y=0. \end(подравнено) \right. $$

След като решихме системата, получаваме: $x_1=0$, $y_1=0$, $\lambda_1=0$ и $x_2=\frac(10)(9)$, $y_2=-\frac(10)( 9)$ , $\lambda_2=-10$. Имаме две стационарни точки: $M_1(0;0)$ и $M_2 \left(\frac(10)(9);-\frac(10)(9) \right)$. Нека открием природата на екстремума във всяка стационарна точка, като използваме детерминантата $H$.

$$H=\ляво| \begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \end(array) \right|= \ляво| \begin(масив) (ccc) 0 & 1 & 1\\ 1 & 8 & -1 \\ 1 & -1 & 18y \end(масив) \right|=-10-18y $$

В точка $M_1(0;0)$ $H=-10-18\cdot 0=-10< 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{\min}=0$. В точке $M_2\left(\frac{10}{9};-\frac{10}{9}\right)$ $H=10 >0$, следователно в тази точка функцията има условен максимум, $z_(\max)=\frac(500)(243)$.

Ние изследваме природата на екстремума във всяка точка, използвайки различен метод, базиран на знака на $d^2F$:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=8dx^2-2dxdy+ 18ydy ^2 $$

От уравнението на връзката $x+y=0$ имаме: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.

$$ d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2 $$

Тъй като $ d^2F \Bigr|_(M_1)=10 dx^2 > 0$, тогава $M_1(0;0)$ е условната минимална точка на функцията $z(x,y)=3y^3+ 4x^ 2-xy$. По същия начин $d^2F \Bigr|_(M_2)=-10 dx^2< 0$, т.е. $M_2\left(\frac{10}{9}; -\frac{10}{9} \right)$ - точка условного максимума.

Втори начин

От уравнението на връзката $x+y=0$ получаваме: $y=-x$. Замествайки $y=-x$ във функцията $z(x,y)=3y^3+4x^2-xy$, получаваме някаква функция на променливата $x$. Нека означим тази функция като $u(x)$:

$$ u(x)=z(x,-x)=3\cdot(-x)^3+4x^2-x\cdot(-x)=-3x^3+5x^2. $$

Така сведохме проблема за намиране на условния екстремум на функция на две променливи до проблема за определяне на екстремума на функция на една променлива.

$$ u_(x)^(")=-9x^2+10x;\\ -9x^2+10x=0; \; x\cdot(-9x+10)=0;\\ x_1=0; \ ; y_1=-x_1=0;\\ x_2=\frac(10)(9);\; y_2=-x_2=-\frac(10)(9). $$

Получихме точки $M_1(0;0)$ и $M_2\left(\frac(10)(9); -\frac(10)(9)\right)$. Допълнителни изследвания са известни от курса на диференциалното смятане на функциите на една променлива. Като изследваме знака на $u_(xx)^("")$ във всяка неподвижна точка или проверяваме промяната в знака на $u_(x)^(")$ в намерените точки, получаваме същите заключения, както когато решаване по първия начин. Например ще проверим знак $u_(xx)^("")$:

$$u_(xx)^("")=-18x+10;\\ u_(xx)^("")(M_1)=10;\;u_(xx)^("")(M_2)=- 10.$$

Тъй като $u_(xx)^("")(M_1)>0$, тогава $M_1$ е минималната точка на функцията $u(x)$ и $u_(\min)=u(0)=0 $ . Тъй като $u_(xx)^("")(M_2)<0$, то $M_2$ - точка максимума функции $u(x)$, причём $u_{\max}=u\left(\frac{10}{9}\right)=\frac{500}{243}$.

Стойностите на функцията $u(x)$ за дадено условие на свързване съвпадат със стойностите на функцията $z(x,y)$, т.е. намерените екстремуми на функцията $u(x)$ са търсените условни екстремуми на функцията $z(x,y)$.

Отговор: в точката $(0;0)$ функцията има условен минимум, $z_(\min)=0$. В точката $\left(\frac(10)(9); -\frac(10)(9) \right)$ функцията има условен максимум, $z_(\max)=\frac(500)(243 )$.

Нека разгледаме друг пример, в който ще изясним природата на екстремума чрез определяне на знака на $d^2F$.

Пример №3

Намерете най-голямата и най-малката стойност на функцията $z=5xy-4$, ако променливите $x$ и $y$ са положителни и удовлетворяват уравнението за свързване $\frac(x^2)(8)+\frac( y^2)(2) -1=0$.

Нека съставим функцията на Лагранж: $F=5xy-4+\lambda \left(\frac(x^2)(8)+\frac(y^2)(2)-1 \right)$. Нека намерим стационарните точки на функцията на Лагранж:

$$ F_(x)^(")=5y+\frac(\lambda x)(4); \; F_(y)^(")=5x+\lambda y.\\ \left \( \begin(aligned) & 5y+\frac(\lambda x)(4)=0;\\ & 5x+\lambda y=0;\\ & \frac(x^2)(8)+\frac(y^2)(2)- 1=0;\\ & x > 0; \;y > 0. \end(aligned) \right. $$

Всички следващи трансформации се извършват, като се вземе предвид $x > 0; \; y > 0$ (това е посочено в формулировката на проблема). От второто уравнение изразяваме $\lambda=-\frac(5x)(y)$ и заместваме намерената стойност в първото уравнение: $5y-\frac(5x)(y)\cdot \frac(x)(4 )=0$ , $4y^2-x^2=0$, $x=2y$. Като заместим $x=2y$ в третото уравнение, получаваме: $\frac(4y^2)(8)+\frac(y^2)(2)-1=0$, $y^2=1$, $y =1$.

Тъй като $y=1$, тогава $x=2$, $\lambda=-10$. Ние определяме природата на екстремума в точката $(2;1)$ въз основа на знака на $d^2F$.

$$ F_(xx)^("")=\frac(\lambda)(4); \; F_(xy)^("")=5; \; F_(yy)^("")=\ламбда. $$

Тъй като $\frac(x^2)(8)+\frac(y^2)(2)-1=0$, тогава:

$$ d\left(\frac(x^2)(8)+\frac(y^2)(2)-1\right)=0; \; d\left(\frac(x^2)(8) \right)+d\left(\frac(y^2)(2) \right)=0; \; \frac(x)(4)dx+ydy=0; \; dy=-\frac(xdx)(4y). $$

По принцип тук можете веднага да замените координатите на стационарната точка $x=2$, $y=1$ и параметъра $\lambda=-10$, получавайки:

$$ F_(xx)^("")=\frac(-5)(2); \; F_(xy)^("")=-10; \; dy=-\frac(dx)(2).\\ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^(" ")dy^2=-\frac(5)(2)dx^2+10dx\cdot \left(-\frac(dx)(2) \right)-10\cdot \left(-\frac(dx) (2) \right)^2=\\ =-\frac(5)(2)dx^2-5dx^2-\frac(5)(2)dx^2=-10dx^2. $$

Въпреки това, в други задачи на условен екстремум може да има няколко стационарни точки. В такива случаи е по-добре да представите $d^2F$ в общ вид и след това да замените координатите на всяка от намерените неподвижни точки в получения израз:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=\frac(\lambda) (4)dx^2+10\cdot dx\cdot \frac(-xdx)(4y) +\lambda\cdot \left(-\frac(xdx)(4y) \right)^2=\\ =\frac (\lambda)(4)dx^2-\frac(5x)(2y)dx^2+\lambda \cdot \frac(x^2dx^2)(16y^2)=\left(\frac(\lambda )(4)-\frac(5x)(2y)+\frac(\lambda \cdot x^2)(16y^2) \right)\cdot dx^2 $$

Замествайки $x=2$, $y=1$, $\lambda=-10$, получаваме:

$$ d^2 F=\left(\frac(-10)(4)-\frac(10)(2)-\frac(10 \cdot 4)(16) \right)\cdot dx^2=- 10dx^2. $$

Тъй като $d^2F=-10\cdot dx^2< 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{\max}=10-4=6$.

Отговор: в точка $(2;1)$ функцията има условен максимум, $z_(\max)=6$.

В следващата част ще разгледаме приложението на метода на Лагранж за функции на по-голям брой променливи.

Екстремуми на функции на няколко променливи. Необходимо условие за екстремум. Достатъчно условие за екстремум. Условен екстремум. Метод на умножителя на Лагранж. Намиране на най-голямата и най-малката стойност.

Лекция 5.

Определение 5.1.Точка M 0 (x 0, y 0)Наречен максимална точкафункции z = f (x, y),Ако f (x o, y o) > f(x,y)за всички точки (x, y) М 0.

Определение 5.2.Точка M 0 (x 0, y 0)Наречен минимална точкафункции z = f (x, y),Ако f (x o, y o) < f(x,y)за всички точки (x, y)от някаква околност на точка М 0.

Забележка 1. Максималните и минималните точки се извикват екстремни точкифункции на няколко променливи.

Забележка 2. Точката на екстремум за функция на произволен брой променливи се определя по подобен начин.

Теорема 5.1 (необходимите условияекстремум). Ако M 0 (x 0, y 0)– екстремна точка на функцията z = f (x, y),тогава в този момент частните производни от първи ред на тази функция са равни на нула или не съществуват.

Доказателство.

Нека фиксираме стойността на променливата при, броене y = y 0. След това функцията f (x, y 0)ще бъде функция на една променлива х, за което x = x 0е екстремната точка. Следователно, по теоремата на Ферма, или не съществува. Същото твърдение се доказва по подобен начин за .

Определение 5.3.Точките, принадлежащи към областта на функция на няколко променливи, в които частните производни на функцията са равни на нула или не съществуват, се наричат стационарни точкитази функция.

Коментирайте. Така екстремумът може да бъде достигнат само в стационарни точки, но не е задължително да се наблюдава във всяка от тях.

Теорема 5.2(достатъчни условия за екстремум). Нека в някои околности на точката M 0 (x 0, y 0), която е неподвижна точка на функцията z = f (x, y),тази функция има непрекъснати частни производни до 3-ти ред включително. Нека означим тогава:

1) f(x,y)има в точката М 0максимум ако AC–B² > 0, А < 0;

2) f(x,y)има в точката М 0минимум ако AC–B² > 0, А > 0;

3) няма екстремум в критичната точка, ако AC–B² < 0;

4) ако AC–B² = 0, необходими са допълнителни изследвания.

Доказателство.

Нека напишем формулата на Тейлър от втори ред за функцията f(x,y),запомняйки, че в стационарна точка частните производни от първи ред са равни на нула:

Където Ако ъгълът между сегмента М 0 М, Където M (x 0 +Δ x, y 0 +Δ при), и оста O хобозначават φ, тогава Δ x =Δ ρ cos φ, Δ y =Δρsinφ. В този случай формулата на Тейлър ще приеме формата: . Нека Тогава можем да разделим и умножим израза в скоби по А. Получаваме:

Нека сега разгледаме четири възможни случая:

1) AC-B² > 0, А < 0. Тогда , и при достатъчно малък Δρ. Следователно в някакъв квартал M 0 f (x 0 + Δ x, y 0 +Δ y)< f (x 0, y 0), това е М 0– максимална точка.

2) Нека AC–B² > 0, А > 0.Тогава , И М 0– минимална точка.

3) Нека AC-B² < 0, А> 0. Разгледайте нарастването на аргументите по лъча φ = 0. Тогава от (5.1) следва, че , тоест при движение по този лъч функцията нараства. Ако се движим по лъч, така че tg φ 0 = -A/B,Че , следователно при движение по този лъч функцията намалява. И така, точка М 0не е екстремна точка.

3`) Кога AC–B² < 0, А < 0 доказательство отсутствия экстремума проводится

подобен на предишния.

3``) Ако AC–B² < 0, А= 0, тогава . При което . Тогава за достатъчно малко φ изразът 2 б cosφ + ° С sinφ е близо до 2 IN, тоест запазва постоянен знак, но sinφ променя знака в близост до точката М 0.Това означава, че нарастването на функцията променя знака в близост до стационарна точка, която следователно не е точка на екстремум.

4) Ако AC–B² = 0 и , , тоест знакът на нарастването се определя от знака на 2α 0. В същото време са необходими допълнителни изследвания за изясняване на въпроса за съществуването на екстремум.

Пример. Нека намерим точките на екстремума на функцията z = x² - 2 xy + 2г² + 2 х.За да намерим стационарни точки, решаваме системата . И така, неподвижната точка е (-2,-1). При което А = 2, IN = -2, СЪС= 4. Тогава AC–B² = 4 > 0, следователно в стационарна точка се достига екстремум, а именно минимум (тъй като А > 0).

Определение 5.4.Ако аргументите на функцията f (x 1, x 2,…, x n)са обвързани с допълнителни условия във формуляра муравнения ( м< n) :

φ 1 ( x 1, x 2,…, x n) = 0, φ 2 ( x 1, x 2,…, x n) = 0, …, φ m ( x 1, x 2,…, x n) = 0, (5.2)

където функциите φ i имат непрекъснати частни производни, тогава се наричат ​​уравнения (5.2). уравнения на връзката.

Определение 5.5.Екстремум на функцията f (x 1, x 2,…, x n)когато са изпълнени условията (5.2), се извиква условен екстремум.

Коментирайте. Можем да предложим следната геометрична интерпретация на условния екстремум на функция от две променливи: нека аргументите на функцията f(x,y)свързани с уравнението φ (x,y)= 0, определяща някаква крива в равнината O xy. Възстановяване на перпендикуляри към равнина O от всяка точка на тази крива xyдокато се пресече с повърхността z = f (x,y),получаваме пространствена крива, лежаща на повърхността над кривата φ (x,y)= 0. Задачата е да се намерят точките на екстремум на получената крива, които, разбира се, в общия случай не съвпадат с безусловните точки на екстремум на функцията f(x,y).

Нека определим необходимите условия за условен екстремум за функция на две променливи, като първо въведем следното определение:

Определение 5.6.функция L (x 1 , x 2 ,…, x n) = f (x 1 , x 2 ,…, x n) + λ 1 φ 1 (x 1 , x 2 ,…, x n) +

+ λ 2 φ 2 (x 1 , x 2 ,…, x n) +…+λ m φ m (x 1 , x 2 ,…, x n), (5.3)

Където λi –някои са постоянни, т.нар Функция на Лагранж, и числата λ i– неопределени множители на Лагранж.

Теорема 5.3(необходими условия за условен екстремум). Условен екстремум на функция z = f (x, y)в присъствието на уравнението на свързване φ ( x, y)= 0 може да се постигне само в стационарни точки на функцията на Лагранж L (x, y) = f (x, y) + λφ (x, y).

Доказателство. Уравнението на свързване определя имплицитна връзка приот х, следователно ще приемем, че приима функция от х: y = y(x).Тогава zима сложна функция от х, а неговите критични точки се определят от условието: . (5.4) От уравнението за свързване следва, че . (5.5)

Нека умножим равенството (5.5) по някакво число λ и го съберем с (5.4). Получаваме:

, или .

Последното равенство трябва да бъде изпълнено в стационарни точки, от което следва:

(5.6)

Получава се система от три уравнения за три неизвестни: x, yи λ, а първите две уравнения са условията за стационарната точка на функцията на Лагранж. Като изключим спомагателното неизвестно λ от системата (5.6), намираме координатите на точките, в които оригиналната функция може да има условен екстремум.

Забележка 1. Наличието на условен екстремум в намерената точка може да се провери чрез изследване на частните производни от втори ред на функцията на Лагранж по аналогия с теорема 5.2.

Забележка 2. Точки, в които може да се достигне условният екстремум на функцията f (x 1, x 2,…, x n)когато са изпълнени условията (5.2), могат да бъдат определени като решения на системата (5.7)

Пример. Нека намерим условния екстремум на функцията z = xyпредвид това x + y= 1. Нека съставим функцията на Лагранж L(x, y) = xy + λ (x + y – 1). Система (5.6) изглежда така:

Където -2λ=1, λ=-0,5, x = y = -λ = 0,5. При което L(x,y)могат да бъдат представени във формата L(x, y) = - 0,5 (x–y)² + 0,5 ≤ 0,5, следователно в намерената неподвижна точка L(x,y)има максимум и z = xy –условен максимум.

Достатъчно условие за екстремум на функция на две променливи

1. Нека функцията е непрекъснато диференцируема в някаква околност на точката и има непрекъснати частни производни от втори ред (чисти и смесени).

2. Нека означим с детерминанта от втори ред

екстремна променлива лекционна функция

Теорема

Ако точката с координати е неподвижна точка за функцията, тогава:

А) При него е точка на локален екстремум, а при локален максимум е локален минимум;

В) в точката не е локална точка на екстремум;

В) ако, може и двете.

Доказателство

Нека напишем формулата на Тейлър за функцията, като се ограничим до два члена:

Тъй като според условията на теоремата точката е неподвижна, частните производни от втори ред са равни на нула, т.е. И. Тогава

Нека обозначим

Тогава увеличението на функцията ще приеме формата:

Поради непрекъснатостта на частичните производни от втори ред (чисти и смесени), съгласно условията на теоремата в точка, можем да запишем:

Къде или; ,

1. Нека и, т.е. или.

2. Умножете увеличението на функцията и разделете на, получаваме:

3. Нека добавим израза във къдрави скоби към пълния квадрат на сумата:

4. Изразът във фигурни скоби е неотрицателен, тъй като

5. Следователно, ако a означава и, тогава и, следователно, според дефиницията, точката е локална минимална точка.

6. Ако a означава и, тогава според дефиницията точката с координати е точка на локален максимум.

2. Разгледайте квадратния трином, неговия дискриминант, .

3. Ако, тогава има такива точки, че полиномът

4. Записваме общото увеличение на функцията в точка в съответствие с израза, получен в I като:

5. Поради непрекъснатостта на частните производни от втори ред, съгласно условията на теоремата в точка, можем да напишем, че

Следователно има околност на точка, така че за всяка точка квадратният трином е по-голям от нула:

6. Разгледайте околността на точка.

Нека изберем произволна стойност, така че точка. Ако приемем, че във формулата за нарастване на функцията

Какво получаваме:

7. От тогава.

8. Като спорим по подобен начин за корена, откриваме, че във всяка -околост на точка има точка, за която следователно в околността на точката не се запазва знак, следователно няма екстремум в точката.

Условен екстремум на функция на две променливи

При намиране на екстремуми на функция на две променливи често възникват проблеми, свързани с така наречения условен екстремум. Тази концепция може да бъде обяснена с помощта на примера на функция на две променливи.

Нека функция и права L са дадени в равнината 0xy. Задачата е да се намери точка P (x, y) на линия L, в която стойността на функцията е най-голямата или най-малката в сравнение със стойностите на тази функция в точки на линия L, разположени близо до точка P. Такива точки P се наричат ​​условни екстремални точки функции на линия L. За разлика от обичайната екстремна точка, стойността на функцията в условната екстремална точка се сравнява със стойностите на функцията не във всички точки от нейния съсед, а само в тези, които лежат на линия L.

Абсолютно ясно е, че точката на обикновен екстремум (те казват още безусловен екстремум) е и точка на условен екстремум за всяка права, минаваща през тази точка. Обратното, разбира се, не е вярно: условната точка на екстремум може да не е обикновената точка на екстремум. Нека илюстрираме това с пример.

Пример №1.Графиката на функцията е горната полусфера (фиг. 2).

Ориз. 2.

Тази функция има максимум в началото; той съответства на върха М на полукълбото. Ако линията L е права линия, минаваща през точки A и B (нейното уравнение), тогава е геометрично ясно, че за точките на тази права най-голямата стойност на функцията се постига в точката, разположена по средата между точките A и B , Това е точката на условния екстремум (максимум) на тази линия; тя съответства на точка М 1 на полусферата и от фигурата става ясно, че тук не може да се говори за обикновен екстремум.

Имайте предвид, че в последната част на задачата за намиране на най-големите и най-малките стойности на функция в затворена област, трябва да намерим екстремните стойности на функцията на границата на тази област, т.е. на някаква линия и по този начин решаване на проблема с условния екстремум.

Определение 1.Те казват, че където има в точка, удовлетворяваща уравнението, условен или относителен максимум (минимум): ако за всяка точка, удовлетворяваща уравнението, неравенството

Определение 2.Уравнение от формата се нарича уравнение на ограничение.

Теорема

Ако функциите и са непрекъснато диференцируеми в околността на точка и частната производна и точката е условна точка на екстремум на функцията по отношение на уравнението на ограничението, тогава детерминантата от втори ред е равна на нула:

Доказателство

1. Тъй като според условията на теоремата, частната производна и стойността на функцията, тогава в определен правоъгълник

дефинирана неявна функция

Сложна функция на две променливи в точка ще има локален екстремум, следователно, или.

2. Действително, според свойството за инвариантност на диференциалната формула от първи ред

3. Уравнението на връзката може да бъде представено в тази форма, което означава

4. Умножете уравнение (2) по и (3) по и ги добавете

Следователно, когато

произволен. и т.н.

Последица

Търсенето на условни точки на екстремум на функция на две променливи на практика се извършва чрез решаване на система от уравнения

И така, в горния пример № 1 от уравнението на връзката имаме. От тук е лесно да се провери при какво достига максимум. Но тогава от комуникационното уравнение. Получаваме точка P, намерена геометрично.

Пример №2.Намерете условните точки на екстремум на функцията спрямо уравнението на свързване.

Нека намерим частните производни дадена функцияи свързващи уравнения:

Нека създадем детерминанта от втори ред:

Нека напишем система от уравнения за намиране на условни точки на екстремум:

Това означава, че има четири точки от условния екстремум на функцията с координати: .

Пример №3.Намерете точките на екстремума на функцията.

Приравнявайки частните производни на нула: , намираме една неподвижна точка - началото. Тук,. Следователно точката (0, 0) не е точка на екстремум. Уравнението е уравнението на хиперболичен параболоид (фиг. 3) от фигурата се вижда, че точката (0, 0) не е точка на екстремум.

Ориз. 3.

Най-голямата и най-малката стойност на функция в затворена област

1. Нека функцията е дефинирана и непрекъсната в ограничена затворена област D.

2. Нека функцията има крайни частни производни в тази област, с изключение на отделни точки от областта.

3. В съответствие с теоремата на Вайерщрас в тази област има точка, в която функцията приема най-големи и най-малки стойности.

4. Ако тези точки са вътрешни точки на областта D, тогава очевидно те ще имат максимум или минимум.

5. В този случай точките, които ни интересуват, са сред подозрителните точки в екстремума.

6. Функцията обаче може също да приеме най-голямата или най-малката стойност на границата на област D.

7. За да намерите най-голямата (най-малката) стойност на функция в област D, трябва да намерите всички вътрешни точки, подозрителни за екстремум, да изчислите стойността на функцията в тях, след което да сравните със стойността на функцията в гранични точки на региона и най-голямата от всички намерени стойности ще бъде най-голямата в затворения регион D.

8. Методът за намиране на локален максимум или минимум беше обсъден по-рано в раздел 1.2. и 1.3.

9. Остава да разгледаме метода за намиране на най-големия и най-ниска стойностфункционира на границата на района.

10. В случай на функция на две променливи, областта обикновено е ограничена от крива или няколко криви.

11. По такава крива (или няколко криви) променливите и или зависят една от друга, или и двете зависят от един параметър.

12. Така на границата функцията се оказва зависима от една променлива.

13. Метод на търсене най-висока стойностфункции на една променлива бяха обсъдени по-рано.

14. Нека границата на област D е дадена чрез параметрични уравнения:

Тогава върху тази крива функцията на две променливи ще бъде сложна функцияот параметър: . За такава функция най-големите и най-малките стойности се определят с помощта на метода за определяне на най-големите и най-малките стойности за функция на една променлива.