McLareni lagunemine. Funktsioonide laiendamine võimsusridadesse

Kui funktsioon f(x) on mõnel intervallil, mis sisaldab punkti A, kõigi järkude tuletised, siis saab sellele rakendada Taylori valemit:

Kus r n– seeria nn jääk liige või jääk, seda saab hinnata Lagrange'i valemi abil:

, kus arv x on vahel X Ja A.

Kui mõne väärtuse eest x r n®0 kl n®¥, siis limiidis muutub Taylori valem selle väärtuse koonduvaks valemiks Taylori sari:

Seega funktsioon f(x) saab kõnealuses punktis laiendada Taylori seeriaks X, Kui:

1) tal on kõikide järjekordade tuletised;

2) konstrueeritud jada selles punktis koondub.

Kell A=0 saame seeria nimega Maclaurini lähedal:

Näide 1 f(x)= 2x.

Lahendus. Leiame funktsiooni ja selle tuletiste väärtused aadressil X=0

f(x) = 2x, f( 0) = 2 0 =1;

f¢(x) = 2x ln2, f¢( 0) = 2 0 ln2 = ln2;

f¢¢(x) = 2x 2 2, f¢¢( 0) = 2 0 ln 2 2 = ln 2 2;

f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2 = ln n 2.

Asendades saadud tuletiste väärtused Taylori seeria valemiga, saame:

Selle seeria lähenemisraadius võrdub lõpmatusega, seega kehtib see laiendus –¥<x<+¥.

Näide 2 X+4) funktsiooni jaoks f(x)= e x.

Lahendus. Funktsiooni e tuletiste leidmine x ja nende väärtused hetkel X=-4.

f(x)= e x, f(-4) = e -4 ;

f¢(x)= e x, f¢(-4) = e -4 ;

f¢¢(x)= e x, f¢¢(-4) = e -4 ;

f(n)(x)= e x, f(n)( -4) = e -4 .

Seetõttu on funktsiooni nõutav Taylori seeria vorm:

See laiendus kehtib ka -¥ jaoks<x<+¥.

Näide 3 . Laiendage funktsiooni f(x)=ln x volituste seerias ( X- 1),

(st Taylori seerias punkti läheduses X=1).

Lahendus. Leia selle funktsiooni tuletised.

Asendades need väärtused valemisse, saame soovitud Taylori seeria:

Kasutades d'Alemberti testi, saate kontrollida, kas seeria koondub millal

½ X- 1½<1. Действительно,

Seeria koondub, kui ½ X- 1½<1, т.е. при 0<x<2. При X=2 saame vahelduva jada, mis vastab Leibnizi kriteeriumi tingimustele. Kell X=0 funktsioon pole määratletud. Seega on Taylori rea konvergentsi piirkonnaks poolavatud intervall (0;2]).

Esitagem sel viisil saadud laiendused Maclaurini seeriasse (s.o. punkti läheduses X=0) mõne elementaarfunktsiooni jaoks:

(2) ,

(3) ,

( nimetatakse viimast lagunemist binoomne jada)

Näide 4 . Laiendage funktsioon astmeseeriaks

Lahendus. Laienduses (1) asendame X peal - X 2, saame:

Näide 5 . Laiendage funktsiooni Maclaurini seerias

Lahendus. Meil on

Kasutades valemit (4), saame kirjutada:

selle asemel asendades X valemisse -X, saame:

Siit leiame:

Sulgusid avades, sarja tingimusi ümber paigutades ja sarnaseid termineid tuues saame

See seeria läheneb intervallile

(-1;1), kuna see on saadud kahest seeriast, millest igaüks koondub selles intervallis.

Kommenteeri .

Valemeid (1)-(5) saab kasutada ka vastavate funktsioonide laiendamiseks Taylori seeriaks, s.t. funktsioonide laiendamiseks positiivsete täisarvude astmetes ( Ha). Selleks on vaja antud funktsioonil sooritada sellised identsed teisendused, et saada üks funktsioonidest (1)-(5), milles selle asemel X maksab k( Ha) m , kus k on konstantne arv, m on positiivne täisarv. Sageli on mugav muuta muutujat t=Ha ja laiendage saadud funktsiooni t suhtes Maclaurini seerias.

See meetod illustreerib teoreemi funktsiooni astmerea laienduse unikaalsuse kohta. Selle teoreemi olemus seisneb selles, et sama punkti naabruses ei ole võimalik saada kahte erinevat astmerida, mis läheneksid samale funktsioonile, olenemata sellest, kuidas seda laiendatakse.

Näide 6 . Laiendage funktsiooni Taylori seerias punkti läheduses X=3.

Lahendus. Selle probleemi saab nagu varemgi lahendada Taylori seeria definitsiooni abil, mille jaoks peame leidma funktsiooni tuletised ja nende väärtused X=3. Siiski on lihtsam kasutada olemasolevat laiendust (5):

Saadud seeria koondub kell või –3<x- 3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

Näide 7 . Kirjutage Taylori seeria võimsustes ( X-1) funktsioonid .

Lahendus.

Seeria koondub kell või 2< x 5 naela.

Funktsionaalsete seeriate hulgas on kõige olulisem koht võimsusseeriatel.

Võimseeria on seeria

mille terminid on kasvavate mittenegatiivsete täisarvude astmetena järjestatud astmefunktsioonid x, A c0 , c 1 , c 2 , c n - konstantsed väärtused. Numbrid c1 , c 2 , c n - seerialiikmete koefitsiendid, c0 - tasuta liige. Astumusrea tingimused on määratletud tervel arvureal.

Tutvume kontseptsiooniga astmeridade lähenemisalad. See on muutuvate väärtuste kogum x, mille jaoks seeria koondub. Võimsusridadel on üsna lihtne lähenemispiirkond. Reaalsete muutujate väärtuste jaoks x lähenemispiirkond koosneb kas ühest punktist või on teatud intervall (konvergentsivahemik) või langeb kokku kogu teljega Ox .

Väärtuste asendamisel võimsusreadesse x= 0 annab tulemuseks arvuseeria

c0 +0+0+...+0+... ,

mis koondub.

Seetõttu, millal x= 0 mis tahes astmerida läheneb ja seetõttu selle lähenemisala ei saa olla tühi komplekt. Kõigi astmeridade lähenemispiirkonna struktuur on sama. Selle saab kindlaks teha järgmise teoreemi abil.

1. teoreem (Abeli ​​teoreem). Kui astmerida läheneb mingile väärtusele x = x 0 , erineb nullist, siis see läheneb ja pealegi absoluutselt kõigi väärtuste puhul |x| < |x 0 | . Pange tähele: nii algväärtust “X on null” kui ka mis tahes “X” väärtust, mida võrreldakse algväärtusega, võetakse modulo – märki arvesse võtmata.

Tagajärg. Kui võimsusseeria lahkneb mingis väärtuses x = x 1 , siis see erineb kõigi väärtuste puhul |x| > |x 1 | .

Nagu me juba varem teada saime, koondub mis tahes astmerida väärtusele x= 0. On astmeridu, mis koonduvad ainult siis, kui x= 0 ja muude väärtuste puhul lahknevad X. Jättes selle juhtumi vaatlusest välja, eeldame, et astmerida läheneb mingile väärtusele x = x 0 , erineb nullist. Siis koondub see vastavalt Abeli ​​teoreemile intervalli ]-| kõikides punktides x0 |, |x 0 |[ (intervall, mille vasak ja parem piir on x väärtused, mille juures astmerida koondub, võttes vastavalt miinus- ja plussmärgiga), sümmeetriline lähtekoha suhtes.

Kui võimsusseeria teatud väärtuse juures lahkneb x = x 1 , siis Abeli ​​teoreemi järelduvuse põhjal lahkneb see kõigis punktides väljaspool lõiku [-| x1 |, |x 1 |] . Sellest järeldub, et iga astmerea jaoks on alguspunkti suhtes sümmeetriline intervall, nn konvergentsi intervall , mille igas punktis seeria koondub, piiridel võib see läheneda või lahkneda, ja mitte tingimata samal ajal, ja väljaspool lõiku seeria lahkneb. Number R nimetatakse astmeridade lähenemisraadiuseks.

Erijuhtudel astmeridade lähenemisintervall võib degenereeruda punktini (siis seeria koondub ainult siis, kui x= 0 ja seda peetakse R= 0) või esindavad tervet arvjoont (siis seeria koondub arvjoone kõikidesse punktidesse ja eeldatakse, et ).

Seega seisneb astmerea konvergentsipiirkonna määramine selle määramises lähenemisraadius R ja ridade konvergentsi uurimine lähenemisintervalli (at ) piiridel.

2. teoreem. Kui kõik astmerea koefitsiendid, alates teatud ühest, erinevad nullist, siis on selle lähenemisraadius võrdne piirväärtusega seeria ühiste järgmiste liikmete koefitsientide absoluutväärtuste suhtes. , st.

Näide 1. Leidke astmeridade konvergentsi piirkond

Lahendus. Siin

Kasutades valemit (28), leiame selle seeria lähenemisraadiuse:

Uurime ridade konvergentsi lähenemisintervalli otstes. Näide 13 näitab, et see jada koondub punktis x= 1 ja lahkneb juures x= -1. Järelikult on lähenemispiirkond poolintervall.

Näide 2. Leidke astmeridade konvergentsi piirkond

Lahendus. Seeria koefitsiendid on positiivsed ja

Leiame selle suhte piiri, s.o. astmeridade lähenemisraadius:

Uurime jada konvergentsi intervalli otstes. Väärtuste asendamine x= -1/5 ja x= 1/5 selles reas annab:

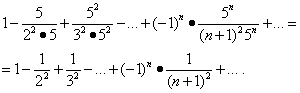
Esimene neist seeriatest läheneb (vt näide 5). Kuid siis lõigu "Absoluutne konvergents" teoreemi kohaselt koondub ka teine ​​seeria ja selle koondumispiirkond on segment

Näide 3. Leidke astmeridade konvergentsi piirkond

Lahendus. Siin

Valemi (28) abil leiame jada lähenemisraadiuse:

Uurime väärtuste seeriate konvergentsi. Asendades need selles seerias, saame vastavalt

Mõlemad seeriad lahknevad seetõttu, et konvergentsi vajalik tingimus ei ole täidetud (nende ühised tingimused ei kipu punktis nullini). Seega see jada lähenemisintervalli mõlemas otsas lahkneb ja selle lähenemispiirkond on intervall.

Näide 5. Leidke astmeridade konvergentsi piirkond

Lahendus. Leiame seose, kus , ja :

Vastavalt valemile (28) selle jada lähenemisraadius

,

see tähendab, et seeria koondub ainult siis, kui x= 0 ja erineb teiste väärtuste puhul X.

Näited näitavad, et lähenemisintervalli lõpus käituvad jadad erinevalt. Näites 1 seeria lähenemisintervalli ühes otsas läheneb ja teises lahkneb; näites 2 koondub see mõlemas otsas; näites 3 see lahkneb mõlemas otsas.

Astumusrea lähenemisraadiuse valem saadakse eeldusel, et kõik seerialiikmete koefitsiendid, alates teatud punktist, erinevad nullist. Seetõttu on valemi (28) kasutamine lubatud ainult nendel juhtudel. Kui seda tingimust rikutakse, tuleks astmeridade lähenemisraadiust otsida kasutades d'Alemberti märk või muutuja asendamisega teisendada seeria vormile, milles määratud tingimus on täidetud.

Näide 6. Leidke astmeridade konvergentsi intervall

Lahendus. See seeria ei sisalda paaritu kraadiga termineid X. Seetõttu muudame seeria, seade . Siis saame sarja

mille konvergentsiraadiuse leidmiseks saame rakendada valemit (28). Kuna , a , siis selle rea lähenemisraadius

Võrdsuselt saame Seega see seeria koondub intervallile .

Jõuridade summa. Astmete ridade diferentseerimine ja integreerimine

Olgu võimuseeria jaoks

lähenemisraadius R> 0, st. see seeria läheneb intervallile .

Siis iga väärtus X konvergentsivahemikust vastab rea teatud summale. Seetõttu on astmeridade summa funktsioon X konvergentsi intervallil. Tähistades seda f(x), saame kirjutada võrdsuse

mõista seda selles mõttes, et seeriate summa igas punktis X konvergentsi intervallist on võrdne funktsiooni väärtusega f(x) sel hetkel. Samas tähenduses ütleme, et astmerida (29) läheneb funktsioonile f(x) lähenemisvahemikul.

Väljaspool konvergentsivahemikku pole võrdusel (30) mõtet.

Näide 7. Leidke astmeridade summa

Lahendus. See on geomeetriline seeria, mille jaoks a= 1, a q= x. Seetõttu on selle summa funktsioon . Seeria läheneb, kui , ja on selle lähenemisintervall. Seega võrdsus

kehtib ainult väärtuste puhul, kuigi funktsioon määratletud kõigi väärtuste jaoks X, välja arvatud X= 1.

Võib tõestada, et astmeridade summa f(x) on pidev ja diferentseeruv lähenemisintervalli mis tahes intervallil, eriti jada lähenemisintervalli mis tahes punktis.

Esitame teoreemid astmeridade terminite kaupa diferentseerimise ja integreerimise kohta.

1. teoreem. Haarusrida (30) selle koondumisvahemikus saab diferentseerida terminite kaupa piiramatu arv kordi ja saadud astmeridade lähenemisraadius on sama kui algsel jada ja nende summad on vastavalt võrdsed .

2. teoreem. Võimsussarja (30) saab integreerida terminite kaupa piiramatu arv kordi vahemikus 0 kuni X, kui , ja saadud astmeridadel on sama lähenemisraadius kui algsel seerial ning nende summad on vastavalt võrdsed

Funktsioonide laiendamine võimsusridadesse

Olgu funktsioon antud f(x), mis vajab laiendamist võimsusreaks, s.o. esindama kujul (30):

Ülesanne on määrata koefitsiendid rida (30). Selleks, eristades võrdsust (30) termini kaupa, leiame järjekindlalt:

……………………………………………….. (31)

Eeldades võrdsustes (30) ja (31) X= 0, leiame

Asendades leitud avaldised võrdsusega (30), saame

(32)

Leiame mõne elementaarfunktsiooni Maclaurini seeria laienduse.

Näide 8. Laiendage funktsiooni Maclaurini seerias

Lahendus. Selle funktsiooni tuletised langevad kokku funktsiooni endaga:

Seetõttu, millal X= 0 meil on

Asendades need väärtused valemiga (32), saame soovitud laienduse:

(33)

See jada koondub tervele arvujoonele (selle lähenemisraadiusele).

16.1. Elementaarfunktsioonide laiendamine Taylori seeriasse ja

Maclaurin

Näitame, et kui hulgal on defineeritud suvaline funktsioon
, punkti läheduses
sellel on palju tuletisi ja see on astmerea summa:

siis leiate selle seeria koefitsiendid.

Asendame võimsusreas
. Siis
.

Leiame funktsiooni esimese tuletise
:

Kell
:
.

Teise tuletise jaoks saame:

Kell
:
.

Selle protseduuri jätkamine n kui saame:
.

Nii saime astmerea kujul:

,

mida nimetatakse Taylori kõrval funktsiooni jaoks
punkti läheduses
.

Taylori seeria erijuhtum on Maclaurin seeria juures
:

Ülejäänud osa Taylori (Maclaurin) seeriast saadakse põhiseeria äraviskamisel n esimesed liikmed ja seda tähistatakse kui
. Siis funktsioon
saab kirjutada summana n sarja esimesed liikmed
ja ülejäänud
:,

.

Ülejäänud on tavaliselt
väljendatakse erinevates valemites.

Üks neist on Lagrange'i kujul:

, Kus
.
.

Pange tähele, et praktikas kasutatakse Maclaurini seeriat sagedamini. Seega funktsiooni kirjutamiseks
astmerea summa kujul on vajalik:

1) leida Maclaurini (Taylori) seeria koefitsiendid;

2) leida saadud astmeridade konvergentsipiirkond;

3) tõestada, et see jada koondub funktsioonile
.

Teoreem1 (vajalik ja piisav tingimus Maclaurini seeria konvergentsi jaoks). Olgu seeria lähenemisraadius
. Selleks, et see seeria intervallis koonduks
funktsioneerima
, tingimuse täitmiseks on vajalik ja piisav:
määratud intervalliga.

2. teoreem. Kui funktsiooni mis tahes järgu tuletised
mingil intervallil
absoluutväärtuses piiratud sama arvuga M, see on
, siis selles intervallis funktsioon
saab laiendada Maclaurini sarjaks.

Näide1 . Laiendage Taylori seerias punkti ümber
funktsiooni.

Lahendus.

.

,;

,
;

,
;

,

.......................................................................................................................................

,
;

Lähenemispiirkond
.

Näide2 . Laiendage funktsiooni Taylori seerias punkti ümber
.

Lahendus:

Leia funktsiooni ja selle tuletiste väärtus kohas
.

,
;

,
;

...........……………………………

,
.

Paneme need väärtused ritta. Saame:

või
.

Leiame selle seeria konvergentsipiirkonna. D'Alemberti testi järgi koondub jada, kui

.

Seetõttu mis tahes see piir on väiksem kui 1 ja seetõttu on seeria konvergentsi vahemik:
.

Vaatleme mitmeid näiteid põhiliste elementaarfunktsioonide laiendamisest Maclaurini seerias. Tuletage meelde, et Maclaurini seeria:

.

koondub intervallile
funktsioneerima
.

Pange tähele, et funktsiooni laiendamiseks seeriasse on vaja:

a) leidke selle funktsiooni jaoks Maclaurini rea koefitsiendid;

b) arvutab saadud jada konvergentsiraadiuse;

c) tõestada, et saadud seeria koondub funktsioonile
.

Näide 3. Mõelge funktsioonile
.

Lahendus.

Arvutame funktsiooni ja selle tuletiste väärtuse at
.

Siis on seeria arvulised koefitsiendid kujul:

kellelegi n. Asendame leitud koefitsiendid Maclaurini seeriaga ja saame:

Leiame saadud seeria lähenemisraadiuse, nimelt:

.

Seetõttu koondub seeria intervallile
.

See seeria läheneb funktsioonile mis tahes väärtuste jaoks , sest igal intervallil
funktsiooni ja selle absoluutväärtuse tuletisinstrumentide arv on piiratud .

Näide4 . Mõelge funktsioonile
.

Lahendus.

:

On lihtne näha, et tuletised on ühtlase järjekorraga
, ja tuletised on paaritu järjestusega. Asendame leitud koefitsiendid Maclaurini seeriaga ja saame laienduse:

Leiame selle jada konvergentsi intervalli. D'Alemberti märgi järgi:

kellelegi . Seetõttu koondub seeria intervallile
.

See seeria läheneb funktsioonile
, sest kõik selle tuletised piirduvad ühtsusega.

Näide5 .
.

Lahendus.

Leiame funktsiooni ja selle tuletiste väärtuse at
:

Seega on selle seeria koefitsiendid:
Ja
, seega:

Sarnaselt eelmisele reale, lähenemisala
. Seeria koondub funktsioonile
, sest kõik selle tuletised piirduvad ühtsusega.

Pange tähele, et funktsioon
paaritu ja seeria laiendamine paaritu astmetes, funktsioon
– ühtlane ja laienemine sarjaks ühtlastes võimsustes.

Näide6 . Binoomseeria:
.

Lahendus.

Leiame funktsiooni ja selle tuletiste väärtuse at
:

Sellest on näha, et:

Asendame need koefitsientide väärtused Maclaurini seeriaga ja saame selle funktsiooni laiendamise astmereaks:

Leiame selle seeria lähenemisraadiuse:

Seetõttu koondub seeria intervallile
. Piiravatel punktidel kl
Ja
jada võib olenevalt eksponendist läheneda või mitte
.

Uuritud seeria koondub intervallile
funktsioneerima
, see tähendab seeriate summat
juures
.

Näide7 . Laiendame funktsiooni Maclaurini seerias
.

Lahendus.

Selle funktsiooni jadaks laiendamiseks kasutame binoomjada at
. Saame:

Tuginedes astmeridade omadusele (võib integreerida astmerida selle konvergentsi piirkonda), leiame selle jada vasaku ja parema külje integraali:

Leiame selle seeria lähenemisala:
,

see tähendab, et selle seeria lähenemisala on intervall
. Määrame jada konvergentsi intervalli otstes. Kell

. See sari on harmooniline sari, see tähendab, et see lahkneb. Kell
saame ühise terminiga arvuseeria
.

Seeria koondub Leibnizi testi järgi. Seega on selle seeria lähenemispiirkond intervall
.

16.2. Võimsusridade rakendamine ligikaudsetes arvutustes

Ligikaudsetes arvutustes on võimsusridadel äärmiselt oluline roll. Nende abiga on koostatud trigonomeetriliste funktsioonide tabelid, logaritmitabelid, muude funktsioonide väärtuste tabelid, mida kasutatakse erinevates teadmiste valdkondades, näiteks tõenäosusteoorias ja matemaatilises statistikas. Lisaks on funktsioonide laiendamine astmereaks kasulik nende teoreetiliseks uurimiseks. Peamine probleem astmeridade kasutamisel ligikaudsetes arvutustes on vea hindamise küsimus rea summa asendamisel selle esimese summaga. n liikmed.

Vaatleme kahte juhtumit:

funktsioon on laiendatud märgi-vahelduvaks seeriaks;

funktsioon on laiendatud konstantse märgi seeriaks.

Arvutamine vahelduvate seeriate abil

Laske funktsioonil
laiendati vahelduvvõimsuse seeriaks. Siis selle funktsiooni arvutamisel konkreetse väärtuse jaoks saame arvuseeria, millele saame rakendada Leibnizi kriteeriumi. Selle kriteeriumi kohaselt, kui rea summa asendatakse selle esimese summaga n termineid, siis absoluutviga ei ületa selle seeria ülejäänud osa esimest liiget, see tähendab:
.

Näide8 . Arvutama
täpsusega 0,0001.

Lahendus.

Kasutame Maclaurini seeriat
, asendades nurga väärtuse radiaanides:

Kui võrrelda antud rea esimest ja teist liiget etteantud täpsusega, siis: .

Kolmas laienemise tähtaeg:

väiksem kui määratud arvutustäpsus. Seetõttu arvutada
piisab, kui jätta seeria kaks terminit, st

.

Seega
.

Näide9 . Arvutama
täpsusega 0,001.

Lahendus.

Kasutame binoomrea valemit. Selleks kirjutame
nagu:
.

Selles väljendis
,

Võrdleme seeria kõiki tingimusi määratud täpsusega. Selge see
. Seetõttu arvutada
piisab, kui jätta seeria kolm terminit.

või
.

Arvutamine positiivsete seeriate abil

Näide10 . Arvutage arv täpsusega 0,001.

Lahendus.

Funktsiooni reas
asendame
. Saame:

Hinnakem viga, mis tekib rea summa asendamisel esimese summaga liikmed. Paneme kirja ilmse ebavõrdsuse:

see on 2<<3. Используем формулу остаточного члена ряда в форме Лагранжа:
,
.

Vastavalt probleemile tuleb leida n nii, et kehtiks järgmine ebavõrdsus:
või
.

Seda on lihtne kontrollida, millal n= 6:
.

Seega
.

Näide11 . Arvutama
täpsusega 0,0001.

Lahendus.

Pange tähele, et logaritmide arvutamiseks võib funktsiooni jaoks kasutada seeriat
, kuid see jada koondub väga aeglaselt ja etteantud täpsuse saavutamiseks oleks vaja võtta 9999 terminit! Seetõttu kasutatakse logaritmide arvutamiseks reeglina funktsiooni seeriat
, mis läheneb intervallile
.

Arvutame
seda sarja kasutades. Lase
, Siis .

Seega
,

Selleks, et arvutada
antud täpsusega võtke esimese nelja liikme summa:
.

Ülejäänud seeria
jätame selle kõrvale. Hindame viga. See on ilmne

või
.

Seega piisas arvutuses kasutatud seerias funktsiooni 9999 asemel võtta ainult neli esimest liiget.
.

Enesediagnostika küsimused

1. Mis on Taylori sari?

2. Millises vormis oli Maclaurini sari?

3. Sõnasta teoreem funktsiooni laiendamise kohta Taylori reas.

4. Kirjutage üles põhifunktsioonide Maclaurini seeria laiendus.

5. Märkige vaadeldavate ridade konvergentsi alad.

6. Kuidas hinnata ligikaudsete arvutuste viga võimsusridade abil?

Funktsiooni laiendamine Taylori, Maclaurini ja Laurenti seeriateks praktiliste oskuste koolitamise saidil. Funktsiooni seeria laiendus võimaldab matemaatikutel hinnata funktsiooni ligikaudset väärtust selle määratluspiirkonna teatud hetkel. Sellist funktsiooni väärtust on palju lihtsam arvutada võrreldes arvutitehnoloogia ajastul nii ebaolulise Bredise tabeli kasutamisega. Funktsiooni laiendamine Taylori seeriasse tähendab selle seeria lineaarfunktsioonide koefitsientide arvutamist ja selle õigel kujul kirjutamist. Õpilased ajavad need kaks seeriat segamini, mõistmata, mis on üldjuhtum ja mis teise puhul erijuhtum. Tuletame teile lõplikult meelde, et Maclaurini seeria on Taylori seeria erijuhtum, see tähendab, et see on Taylori seeria, kuid punktis x = 0. Kõik lühikirjed tuntud funktsioonide laiendamiseks, nagu e^x, Sin(x), Cos(x) ja teised, need on Taylori seeria laiendused, kuid argumendi punktis 0. Keerulise argumendi funktsioonide puhul on Laurent'i seeria TFCT-s kõige levinum probleem, kuna see esindab kahepoolset lõpmatut jada. See on kahe seeria summa. Soovitame vaadata lagundamise näidet otse veebisaidil; seda on väga lihtne teha, klõpsates suvalise numbriga "Näide" ja seejärel nupul "Lahendus". Just see funktsiooni laiendamine jadaks, mis on seotud suuremate jadatega, piirab algfunktsiooni teatud piirkonnas piki ordinaattelge, kui muutuja kuulub abstsisspiirkonda. Vektoranalüüsi võrreldakse teise huvitava matemaatika distsipliiniga. Kuna iga terminit tuleb uurida, võtab protsess üsna palju aega. Mis tahes Taylori seeriat saab seostada Maclaurini seeriaga, asendades x0 nulliga, kuid Maclaurini seeria puhul pole mõnikord ilmne, et Taylori seeriat tagurpidi kujutataks. Justkui seda puhtal kujul ei nõutagi, on see huvitav üldiseks enesearenguks. Iga Laurent'i seeria vastab kahepoolsele lõpmatule astmereale z-a täisarvudes, teisisõnu sama Taylori tüüpi, kuid koefitsientide arvutamisel veidi erinevale jadale. Laurenti seeria konvergentsipiirkonnast räägime veidi hiljem, pärast mitmeid teoreetilisi arvutusi. Nagu eelmisel sajandil, on vaevalt võimalik funktsiooni järkjärgulist jadaks laiendamist saavutada lihtsalt terminite viimisega ühisele nimetajale, kuna nimetajates olevad funktsioonid on mittelineaarsed. Funktsionaalse väärtuse ligikaudne arvutamine on vajalik ülesannete sõnastamiseks. Mõelge sellele, et kui Taylori seeria argument on lineaarne muutuja, siis laienemine toimub mitmes etapis, kuid pilt on täiesti erinev, kui laiendatava funktsiooni argumendiks on kompleksne või mittelineaarne funktsioon, siis protsess sellise funktsiooni esitamine astmereas on ilmne, kuna sel viisil on seega lihtne arvutada, ehkki ligikaudne väärtus, mis tahes punktis definitsioonipiirkonnas minimaalse veaga, millel on vähe mõju edasistele arvutustele. See kehtib ka Maclaurini seeria kohta. kui on vaja arvutada funktsioon nullpunktis. Laurenti seeriat ennast esindab siin aga laiendus lennukis mõtteliste üksustega. Samuti ei jää eduta probleemi õige lahendamine kogu protsessi käigus. Seda lähenemist matemaatikas ei tunta, kuid see on objektiivselt olemas. Selle tulemusena võite jõuda nn punktipõhiste alamhulkade järeldusele ja funktsiooni laiendamisel reas peate kasutama selle protsessi jaoks tuntud meetodeid, näiteks tuletiste teooria rakendamist. Taaskord veendume, et õigus oli õpetajal, kes tegi oma oletused järelarvutuste tulemuste kohta. Pangem tähele, et kõigi matemaatika kaanonite järgi saadud Taylori seeria on olemas ja on määratletud kogu numbriteljel, kuid kallid saiditeenuse kasutajad, ärge unustage algse funktsiooni tüüpi, sest see võib osutuda et esialgu on vaja paika panna funktsiooni definitsioonipiirkond ehk kirjutada ja jätta edasisest vaatlusest välja need punktid, kus funktsioon ei ole reaalarvude valdkonnas defineeritud. Nii-öelda näitab see teie tõhusust probleemi lahendamisel. Nullargumendi väärtusega Maclaurini seeria konstrueerimine ei ole erand sellest, mida on öeldud. Funktsiooni määratluspiirkonna leidmise protsess ei ole katkestatud ja sellele matemaatilisele tehtele tuleb suhtuda täie tõsidusega. Põhiosa sisaldava Laurent'i seeria puhul nimetatakse parameetrit "a" isoleeritud ainsuse punktiks ja Laurent'i seeriat laiendatakse ringina - see on selle osade lähenemisalade ristumiskoht, seega järgneb vastav teoreem. Kuid kõik pole nii keeruline, kui kogenematule õpilasele esmapilgul võib tunduda. Olles uurinud Taylori seeriat, saate hõlpsasti mõista Laurenti seeriat - üldistatud juhtumit numbrite ruumi laiendamiseks. Funktsiooni mis tahes jadalaiendust saab teostada ainult funktsiooni määratluspiirkonna punktis. Arvesse tuleks võtta funktsioonide omadusi, nagu perioodilisus või lõpmatu diferentseeritavus. Samuti soovitame teil kasutada Taylori seeria valmis elementaarfunktsioonide laienduste tabelit, kuna ühte funktsiooni saab esitada kuni kümnete erinevate astmeridadega, nagu on näha meie veebikalkulaatorist. Maclaurini veebiseeriat on lihtne kindlaks teha, kui kasutate ainulaadset veebisaiditeenust, peate lihtsalt sisestama õige kirjaliku funktsiooni ja saate esitatud vastuse mõne sekundiga, see on garanteeritud, et see on täpne ja korrektne. standardne kirjalik vorm. Saate kopeerida tulemuse otse puhtasse koopiasse, et see õpetajale esitada. Õige oleks esmalt määrata kõnealuse funktsiooni analüütilisus rõngastes ja seejärel ühemõtteliselt väita, et see on Laurent'i seerias laiendatav kõigis sellistes rõngastes. Oluline on mitte unustada negatiivseid jõude sisaldavaid Laurenti seeria tingimusi. Keskenduge sellele nii palju kui võimalik. Kasutage hästi Laurenti teoreemi funktsiooni laiendamise kohta täisarvude astmetes.

Kui funktsioonil f(x) on teatud intervalli, mis sisaldab punkti a, kõigi järkude tuletised, saab sellele rakendada Taylori valemit:
,
Kus r n– seeria nn jääk liige või jääk, seda saab hinnata Lagrange'i valemi abil:
, kus arv x on x ja a vahel.

Funktsioonide sisestamise reeglid:

Kui mõne väärtuse eest X r n→0 kl n→∞, siis piirväärtuses muutub Taylori valem selle väärtuse jaoks koonduvaks Taylori sari:
,
Seega saab funktsiooni f(x) vaadeldavas punktis x laiendada Taylori seeriaks, kui:
1) tal on kõikide järjekordade tuletised;
2) konstrueeritud jada selles punktis koondub.

Kui a = 0, saame jada nimega Maclaurini lähedal:
,
Maclaurini seeria kõige lihtsamate (elementaarsete) funktsioonide laiendamine:
Eksponentfunktsioonid
, R=∞
Trigonomeetrilised funktsioonid
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funktsioon actgx ei laiene x astmetes, sest ctg0=∞
Hüperboolsed funktsioonid


Logaritmilised funktsioonid
, -1
Binoomjada
.

Näide nr 1. Laiendage funktsioon astmeseeriaks f(x)= 2x.
Lahendus. Leiame funktsiooni ja selle tuletiste väärtused aadressil X=0
f(x) = 2x, f( 0) = 2 0 =1;
f"(x) = 2x ln2, f"( 0) = 2 0 ln2 = ln2;
f""(x) = 2x 2 2, f""( 0) = 2 0 ln 2 2 = ln 2 2;
…
f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2 = ln n 2.
Asendades saadud tuletiste väärtused Taylori seeria valemiga, saame:

Selle jada lähenemisraadius on võrdne lõpmatusega, seetõttu kehtib see laiendus -∞<x<+∞.

Näide nr 2. Kirjutage Taylori seeria võimsustes ( X+4) funktsiooni jaoks f(x)= e x.
Lahendus. Funktsiooni e tuletiste leidmine x ja nende väärtused hetkel X=-4.
f(x)= e x, f(-4) = e -4 ;
f"(x)= e x, f"(-4) = e -4 ;
f""(x)= e x, f""(-4) = e -4 ;
…
f(n)(x)= e x, f(n)( -4) = e -4 .
Seetõttu on funktsiooni nõutav Taylori seeria vorm:

See laiendus kehtib ka -∞ korral<x<+∞.

Näide nr 3. Laiendage funktsiooni f(x)=ln x volituste seerias ( X- 1),
(st Taylori seerias punkti läheduses X=1).
Lahendus. Leia selle funktsiooni tuletised.
f(x)=lnx , , , ,

f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Asendades need väärtused valemisse, saame soovitud Taylori seeria:

D'Alemberti testi abil saate kontrollida, et seeria koondub ½x-1½<1 . Действительно,

Seeria koondub, kui ½ X- 1½<1, т.е. при 0<x<2. При X=2 saame vahelduva jada, mis vastab Leibnizi kriteeriumi tingimustele. Kui x=0, ei ole funktsioon defineeritud. Seega on Taylori rea konvergentsi piirkonnaks poolavatud intervall (0;2]).

Näide nr 4. Laiendage funktsioon astmeseeriaks.
Lahendus. Laienduses (1) asendame x väärtusega -x 2, saame:
, -∞

Näide nr 5. Laiendage funktsiooni Maclaurini seeriaks.
Lahendus. Meil on
Kasutades valemit (4), saame kirjutada:

asendades valemis x asemel -x, saame:

Siit leiame: ln(1+x)-ln(1-x) = -
Sulgusid avades, sarja tingimusi ümber paigutades ja sarnaseid termineid tuues saame
. See jada koondub intervallisse (-1;1), kuna see saadakse kahest seeriast, millest igaüks läheneb selles intervallis.

Kommenteeri .
Valemeid (1)-(5) saab kasutada ka vastavate funktsioonide laiendamiseks Taylori seeriaks, s.t. funktsioonide laiendamiseks positiivsete täisarvude astmetes ( Ha). Selleks on vaja antud funktsioonil sooritada sellised identsed teisendused, et saada üks funktsioonidest (1)-(5), milles selle asemel X maksab k( Ha) m , kus k on konstantne arv, m on positiivne täisarv. Sageli on mugav muuta muutujat t=Ha ja laiendage saadud funktsiooni t suhtes Maclaurini seerias.

See meetod põhineb teoreemil funktsiooni laiendamise kordumatuse kohta astmereas. Selle teoreemi olemus seisneb selles, et sama punkti naabruses ei ole võimalik saada kahte erinevat astmerida, mis läheneksid samale funktsioonile, olenemata sellest, kuidas seda laiendatakse.

Näide nr 5a. Laiendage funktsiooni Maclaurini seerias ja märkige lähenemispiirkond.
Lahendus. Kõigepealt leiame 1-x-6x 2 =(1-3x)(1+2x) , .
algklassidesse:

Murdu 3/(1-3x) võib lugeda lõpmatult kahaneva geomeetrilise progressiooni summaks nimetajaga 3x, kui |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

konvergentsipiirkonnaga |x|< 1/3.

Näide nr 6. Laiendage funktsioon Taylori seeriaks punkti x = 3 läheduses.
Lahendus. Selle probleemi saab nagu varemgi lahendada Taylori seeria definitsiooni abil, mille jaoks peame leidma funktsiooni tuletised ja nende väärtused X=3. Siiski on lihtsam kasutada olemasolevat laiendust (5):
=
Saadud jada läheneb või –3

Näide nr 7. Kirjutage Taylori seeria funktsiooni ln(x+2) astmetes (x -1).
Lahendus.


Seeria läheneb väärtusele , või -2< x < 5.

Näide nr 8. Laiendage funktsioon f(x)=sin(πx/4) Taylori jadaks punkti x =2 läheduses.
Lahendus. Teeme asenduseks t=x-2:

Kasutades laiendust (3), milles asendame x asemel π / 4 t, saame:

Saadud seeria koondub antud funktsioonile punktis -∞< π / 4 t<+∞, т.е. при (-∞Seega
, (-∞

Ligikaudsed arvutused võimsusridade abil

• kui saadud seeria on vahelduv, kasutatakse järgmist omadust: vahelduva seeria puhul, mis vastab Leibnizi tingimustele, ei ületa ülejäänud seeria absoluutväärtuses esimest kõrvalejäetud liiget.
• kui antud jada on konstantse märgiga, võrreldakse kõrvalejäetud terminitest koosnevat jada lõpmatult kahaneva geomeetrilise progressiooniga.
• Üldjuhul saate ülejäänud Taylori seeria hindamiseks kasutada Lagrange'i valemit: a x ).

Näide nr 1. Arvutage ln(3) 0,01 täpsusega.
Lahendus. Kasutame laiendust, kus x=1/2 (vt eelmise teema näidet 5):

Kontrollime, kas saame ülejäänud kolme laiendusliikme järel kõrvale jätta, selleks hindame seda lõpmatult kahaneva geomeetrilise progressiooni summaga:

Seega võime selle jäägi ära visata ja saada

Näide nr 2. Arvutage 0,0001 täpsusega.
Lahendus. Kasutame binoomjada. Kuna 5 3 on 130-le lähim täisarvu kuup, on soovitav esitada arvu 130 kujul 130 = 5 3 +5.



kuna juba Leibnizi kriteeriumile vastava tulemuseks oleva vahelduva seeria neljas liige on nõutavast täpsusest väiksem:
, seega võib selle ja sellele järgnevatest terminitest loobuda.
Paljusid praktiliselt vajalikke kindlaid või ebaõigeid integraale ei saa arvutada Newtoni-Leibnizi valemi abil, sest selle rakendamine on seotud antiderivaadi leidmisega, millel elementaarfunktsioonides sageli avaldist ei ole. Juhtub ka seda, et antiderivaadi leidmine on võimalik, kuid see on tarbetult töömahukas. Kui aga integrandfunktsioon on laiendatud astmereaks ja integreerimise piirid kuuluvad selle jada konvergentsi intervalli, siis on integraali ligikaudne arvutamine etteantud täpsusega võimalik.

Näide nr 3. Arvutage integraal ∫ 0 1 4 sin (x) x täpsusega 10 -5 .
Lahendus. Vastavat määramatut integraali ei saa väljendada elementaarfunktsioonides, s.t. tähistab "mittepüsivat integraali". Newtoni-Leibnizi valemit ei saa siin rakendada. Arvutame integraali ligikaudselt.
Patu jada termini kaupa x peal x, saame:

Integreerides selle seeria termini kaupa (see on võimalik, kuna integreerimise piirid kuuluvad selle seeria lähenemisvahemikku), saame:

Kuna saadud seeria vastab Leibnizi tingimustele ja soovitud väärtuse saamiseks etteantud täpsusega piisab, kui võtta kahe esimese liikme summa.
Seega leiame
.

Näide nr 4. Arvutage integraal ∫ 0 1 4 e x 2 täpsusega 0,001.
Lahendus.
. Kontrollime, kas saame ülejäänud osa ära visata pärast saadud seeria teist liiget.
0,0001<0.001. Следовательно, .