Etsi varianssi ja keskihajonta. Keskihajonnan laskenta Microsoft Excelissä

Vastaukset kansanterveyttä ja terveydenhuoltoa koskeviin tenttikysymyksiin.
1. Kansanterveys ja terveydenhuolto tieteenä ja käytännön toiminnan alana. Päätavoitteet. Objekti, tutkimuskohde. menetelmät.
2. Terveydenhuolto. Määritelmä. Terveydenhuollon kehityksen historia. Nykyaikaiset terveydenhuoltojärjestelmät, niiden ominaisuudet.
3. Valtion politiikka kansanterveyden suojelun alalla (Valko-Venäjän tasavallan terveydenhuoltolaki). Julkisen terveydenhuollon organisaatioperiaatteet.
4. Vakuutukset ja yksityiset terveydenhuollon muodot.
5. Ennaltaehkäisy, määritelmä, periaatteet, nykyajan ongelmat. Ennaltaehkäisyn tyypit, tasot, ohjeet.
6. Kansalliset ehkäisyohjelmat. Niiden rooli kansanterveyden parantamisessa.
7. Lääketieteellinen etiikka ja deontologia. Käsitteen määritelmä. Nykyajan lääketieteen etiikan ja deontologian ongelmat, ominaisuudet.
8. Terveet elämäntavat, käsitteen määrittely. Terveiden elämäntapojen sosiaaliset ja lääketieteelliset näkökohdat (terveelliset elämäntavat).
9. Hygieniakoulutus, määritelmä, perusperiaatteet. Hygieniakoulutuksen ja -kasvatuksen menetelmät ja keinot. Luennon vaatimukset, terveystiedote.
10. Väestön terveys, kansanterveyteen vaikuttavat tekijät. Terveyskaava. Kansanterveyttä kuvaavat indikaattorit. Analyysikaavio.
11. Väestötiede tieteenä, määritelmä, sisältö. Väestötietojen merkitys terveydenhuollossa.
12. Väestötilasto, tutkimusmenetelmät. Väestölaskennat. Väestön ikärakenteiden tyypit.
13. Väestön mekaaninen liike. Muuttoliikeprosessien ominaisuudet, niiden vaikutukset väestön terveysindikaattoreihin.
14. Hedelmällisyys lääketieteellisenä ja sosiaalisena ongelmana. Indikaattorien laskentamenetelmät. Hedelmällisyystasot WHO:n tietojen mukaan. Moderneja suuntauksia.
15. Erityiset hedelmällisyysindikaattorit (hedelmällisyysindikaattorit). Väestön lisääntyminen, lisääntymistyypit. Indikaattorit, laskentamenetelmät.
16. Kuolleisuus lääketieteellisenä ja sosiaalisena ongelmana. Tutkimusmetodologia, indikaattorit. Kokonaiskuolleisuus WHO:n tietojen mukaan. Moderneja suuntauksia.
17. Imeväiskuolleisuus lääketieteellisenä ja sosiaalisena ongelmana. Sen tason määräävät tekijät.
18. Äitiys- ja perinataalikuolleisuus, tärkeimmät syyt. Indikaattorit, laskentamenetelmät.
19. Väestön luonnollinen liikkuvuus, siihen vaikuttavat tekijät. Indikaattorit, laskentamenetelmät. Luonnollisen liikkeen perusmallit Valko-Venäjällä.
20. Perhesuunnittelu. Määritelmä. Nykyajan ongelmat. Lääketieteelliset organisaatiot ja perhesuunnittelupalvelut Valko-Venäjän tasavallassa.
21. Sairastavuus lääketieteellisenä ja sosiaalisena ongelmana. Modernit trendit ja piirteet Valko-Venäjän tasavallassa.
22. Väestön neuropsyykkisen terveyden lääketieteelliset ja sosiaaliset näkökohdat. Psykoneurologisen hoidon järjestäminen
23. Alkoholismi ja huumeriippuvuus lääketieteellisenä ja sosiaalisena ongelmana
24. Verenkiertoelinten sairaudet lääketieteellisenä ja sosiaalisena ongelmana. Riskitekijät. Ennaltaehkäisyn ohjeet. Sydänhoidon järjestäminen.
25. Pahanlaatuiset kasvaimet lääketieteellisenä ja sosiaalisena ongelmana. Ennaltaehkäisyn pääsuunnat. Onkologisen hoidon järjestäminen.
26. Kansainvälinen tilastollinen sairauksien luokittelu. Rakentamisen periaatteet, käyttötapa. Sen merkitys väestön sairastuvuuden ja kuolleisuuden tutkimuksessa.
27. Väestön sairastuvuuden tutkimusmenetelmät, niiden vertailuominaisuudet.
Metodologia yleisen ja primaarisen sairastuvuuden tutkimiseksi
Yleisen ja ensisijaisen sairastuvuuden indikaattorit.
Tartuntatautien indikaattorit.
Pääindikaattorit, jotka kuvaavat tärkeintä ei-epideemista sairastuvuutta.
Tärkeimmät "sairaalapotilaiden" indikaattorit:
4) Sairaudet, joilla on tilapäinen vamma (kysymys 30)
Tärkeimmät indikaattorit sairastuvuuden analysointiin VUT:n kanssa.
31. Sairastavuuden tutkimus väestön ennaltaehkäisevien tutkimusten perusteella, ennaltaehkäisevien tutkimusten tyypit, menettelytapa. Terveysryhmät. Käsite "patologinen kiintymys".
32. Sairastavuus kuolinsyytietojen mukaan. Tutkimusmetodologia, indikaattorit. Lääketieteellinen kuolintodistus.
Tärkeimmät kuolinsyihin perustuvat sairastuvuusindikaattorit:
33. Vammaisuus lääketieteellisenä ja sosiaalisena ongelmana Käsitteen määritelmä, indikaattorit. Vammaissuuntaukset Valko-Venäjän tasavallassa.
Vammaissuuntaukset Valko-Venäjän tasavallassa.
34. Perusterveydenhuolto, määritelmä, sisältö, rooli ja paikka väestön terveydenhuoltojärjestelmässä. Päätoiminnot.
35. Perusterveydenhuollon perusperiaatteet. Perusterveydenhuollon lääketieteelliset organisaatiot.
36. Väestölle avohoidossa annettavan sairaanhoidon järjestäminen. Perusperiaatteet. toimielimet.
37. Lääkärinhoidon järjestäminen sairaalaympäristössä. toimielimet. Sairaalahoidon tarjoamisen indikaattorit.
38. Sairaanhoidon tyypit. Erityissairaanhoidon järjestäminen väestölle. Erikoissairaanhoidon keskukset, niiden tehtävät.
39. Pääsuunnat laitoshoidon ja erikoissairaanhoidon parantamiseksi Valko-Venäjän tasavallassa.
40. Naisten ja lasten terveyden suojelu Valko-Venäjän tasavallassa. Ohjaus. Lääketieteelliset organisaatiot.
41. Naisten terveyden nykyajan ongelmat. Synnytys- ja gynekologisen hoidon järjestäminen Valko-Venäjän tasavallassa.
42. Lasten lääketieteellisen ja ennaltaehkäisevän hoidon järjestäminen. Johtavat ongelmat lasten terveydessä.
43. Maaseutuväestön terveydenhuollon järjestäminen, maaseudun asukkaiden sairaanhoidon perusperiaatteet. Tasot. Organisaatiot.
Vaihe II – alueellinen lääkäriliitto (TMO).
Vaihe III – aluesairaala ja alueelliset hoitolaitokset.
45. Lääketieteellinen ja sosiaalinen tutkimus (MSE), määritelmä, sisältö, peruskäsitteet.
46. Kuntoutus, määritelmä, tyypit. Valko-Venäjän tasavallan laki "vammaisten henkilöiden vammaisuuden ehkäisystä ja kuntouttamisesta".
47. Lääketieteellinen kuntoutus: käsitteen määrittely, vaiheet, periaatteet. Lääketieteellinen kuntoutuspalvelu Valko-Venäjän tasavallassa.
48. Kaupungin klinikka, rakenne, tehtävät, johtaminen. Klinikan keskeiset suoritusindikaattorit.
Klinikan keskeiset suoritusindikaattorit.
49. Paikallinen periaate väestön avohoidon järjestämisestä. Tonttien tyypit. Alueellinen terapeuttinen alue. Standardit. Paikallisen lääkäri-terapeutin työn sisältö.
Paikallisen terapeutin työn organisointi.
50. Klinikan tartuntatautitoimisto. Lääkärin työskentelytavat ja työtavat tartuntatautien toimistossa.
52. Tärkeimmät indikaattorit, jotka kuvaavat ambulanssihavainnoinnin laatua ja tehokkuutta. Niiden laskentamenetelmä.
53. Klinikan lääketieteellisen kuntoutuksen (MR) osasto. Rakenne, tehtävät. Menettely potilaiden lähettämiseksi OMR:ään.
54. Lastenklinikka, rakenne, tehtävät, työosuudet. Lasten sairaanhoidon ominaisuudet avohoidossa.
55. Paikallisen lastenlääkärin työn pääkohdat. Hoidon ja ennaltaehkäisevän työn sisältö. Viestintä työssä muiden hoito- ja ehkäisylaitosten kanssa. Dokumentointi.
56. Paikallisen lastenlääkärin ennaltaehkäisevän työn sisältö. Vastasyntyneiden sairaanhoidon järjestäminen.
57. Synnytysneuvolan työn rakenne, organisaatio, sisältö. Indikaattorit raskaana olevien naisten palvelutyöstä. Dokumentointi.
58. Synnytyssairaala, rakenne, työn organisointi, johtaminen. Synnytyssairaalan suorituskykymittarit. Dokumentointi.
59. Kaupungin sairaala, sen tehtävät, rakenne, keskeiset tunnusluvut. Dokumentointi.
60. Sairaalan vastaanottoosaston työn organisointi. Dokumentointi. Toimenpiteet sairaalainfektioiden ehkäisemiseksi. Terapeuttinen ja suojaava järjestelmä.
Osa 1. Tiedot hoito- ja ehkäisyorganisaation osastoista ja asennuksista.
Kohta 2. Hoito- ja ehkäisyorganisaation henkilöstö kertomusvuoden lopussa.
Osa 3. Klinikan lääkäreiden työ (poliklinikka), ambulanssi, konsultaatiot.
§ 4. Ennaltaehkäisevät lääkärintarkastukset ja lääketieteellisen ja ennaltaehkäisevän organisaation hammaslääketieteen (hammaslääkärin) ja kirurgian toimistojen työ.
Osa 5. Lääketieteellisten ja apuosastojen (toimistojen) työ.
Osa 6. Diagnostisten osastojen toiminta.
62. Vuosikertomus sairaalan toiminnasta (lomake 14), valmistelumenettely, rakenne. Sairaalan keskeiset suoritusindikaattorit.
Osa 1. Sairaalassa olevien potilaiden kokoonpano ja hoidon tulokset
2 § Muihin sairaaloihin 0-6 vuorokauden iässä siirrettyjen sairaiden vastasyntyneiden kokoonpano ja hoidon tulokset
Osa 3. Sänkykapasiteetti ja sen käyttö
Osa 4. Sairaalan kirurgiset työt
63. Raportti raskaana olevien, synnyttävien ja synnyttäneiden naisten sairaanhoidosta (f. 32), rakenne. Perusindikaattorit.
Osa I. Synnytysneuvolan toiminta.
Osa II. Synnytys sairaalassa
Osa III. Äitiyskuolleisuus
IV jakso. Tietoa synnytyksistä
64. Lääketieteellinen geneettinen neuvonta, päälaitokset. Sen rooli perinataalisen ja lapsikuolleisuuden ehkäisyssä.
65. Lääketieteellinen tilasto, sen osat, tehtävät. Tilastollisen menetelmän rooli väestön terveyden ja terveydenhuoltojärjestelmän suorituskyvyn tutkimuksessa.
66. Tilastollinen perusjoukko. Määritelmä, tyypit, ominaisuudet. Otospopulaation tilastollisen tutkimuksen ominaisuudet.
67. Otospopulaatio, sen vaatimukset. Otospopulaation muodostamisen periaate ja menetelmät.
68. Havaintoyksikkö. Määritelmä, kirjanpitoominaisuuksien ominaisuudet.
69. Tilastollisen tutkimuksen organisointi. Vaiheiden ominaisuudet.
70. Tilastollisen tutkimuksen suunnitelman ja ohjelman sisältö. Tilastollisten tutkimussuunnitelmien tyypit. Tarkkailuohjelma.
71. Tilastollinen havainto. Jatkuva ja ei-jatkuva tilastollinen tutkimus. Epätäydellisen tilastollisen tutkimuksen tyypit.
72. Tilastollinen havainnointi (aineiston kerääminen). Virheitä tilastollisissa havainnoissa.
73. Tilastollinen ryhmittely ja yhteenveto. Typologinen ja vaihteleva ryhmittely.
74. Tilastotaulukot, tyypit, rakennevaatimukset.

81. Keskihajonta, laskentamenetelmä, sovellus.

Likimääräinen menetelmä variaatiosarjan vaihtelun arvioimiseksi on rajan ja amplitudin määrittäminen, mutta sarjan muunnelman arvoja ei oteta huomioon. Yleisin yleisesti hyväksytty kvantitatiivisen ominaisuuden vaihtelun mitta variaatiosarjassa on keskihajonta (σ - sigma). Mitä suurempi keskihajonta, sitä suurempi on tämän sarjan vaihteluaste.

Keskihajonnan laskentamenetelmä sisältää seuraavat vaiheet:

1. Etsi aritmeettinen keskiarvo (M).

2. Määritä yksittäisten vaihtoehtojen poikkeamat aritmeettisesta keskiarvosta (d=V-M). Lääketieteessä poikkeamat keskiarvosta merkitään d:llä (poikkeama). Kaikkien poikkeamien summa on nolla.

3. Neliöi jokainen poikkeama d 2.

4. Kerro poikkeamien neliöt vastaavilla taajuuksilla d 2 *p.

5. Laske tulojen summa (d 2 *p)

6. Laske standardipoikkeama kaavalla:

kun n on suurempi kuin 30, tai
kun n on pienempi tai yhtä suuri kuin 30, missä n on kaikkien vaihtoehtojen lukumäärä.

Keskihajonnan arvo:

1. Keskihajonta kuvaa muunnelman hajoamista suhteessa keskiarvoon (eli variaatiosarjan vaihteluun). Mitä suurempi sigma, sitä suurempi on tämän sarjan monimuotoisuus.

2. Keskihajonnan avulla arvioidaan vertailevasti aritmeettisen keskiarvon vastaavuusastetta variaatiosarjaan, jolle se on laskettu.

Massailmiöiden vaihtelut noudattavat normaalijakauman lakia. Tätä jakaumaa edustava käyrä näyttää sileältä kellon muotoiselta symmetriseltä käyrältä (Gaussin käyrä). Todennäköisyysteorian mukaan ilmiöissä, jotka noudattavat normaalijakauman lakia, aritmeettisen keskiarvon ja keskihajonnan välillä on tiukka matemaattinen suhde. Homogeenisen variaatiosarjan variantin teoreettinen jakauma noudattaa kolmen sigman sääntöä.

Jos suorakaiteen muotoisessa koordinaattijärjestelmässä kvantitatiivisen ominaisuuden (muunnelmien) arvot piirretään abskissa-akselille ja variaatiosarjan muunnelman esiintymistiheys piirretään ordinaatta-akselille, niin variantit, joissa on suurempi ja pienempi arvot sijaitsevat tasaisesti aritmeettisen keskiarvon sivuilla.

On todettu, että ominaisuuden normaalijakaumalla:

68,3 % option arvoista on M1:n sisällä

95,5 % option arvoista on M2:n sisällä

99,7 % option arvoista on M3:n sisällä

3. Keskihajonnan avulla voit määrittää normaaliarvot kliinisille ja biologisille parametreille. Lääketieteessä väli M1 otetaan yleensä tutkittavan ilmiön normaalialueeksi. Arvioidun arvon poikkeama aritmeettisesta keskiarvosta yli 1 tarkoittaa tutkitun parametrin poikkeamaa normista.

4. Lääketieteessä kolmen sigman sääntöä käytetään pediatriassa lasten fyysisen kehityksen yksilölliseen arviointiin (sigmapoikkeamamenetelmä), lastenvaatteiden standardien kehittämiseen.

5. Keskihajonta on tarpeen tutkittavan ominaisuuden monimuotoisuuden karakterisoimiseksi ja aritmeettisen keskiarvon virheen laskemiseksi.

Keskihajonnan arvoa käytetään yleensä vertaamaan samantyyppisten sarjojen vaihtelua. Jos verrataan kahta sarjaa, joilla on erilaiset ominaisuudet (pituus ja paino, sairaalahoidon keskimääräinen kesto ja sairaalakuolleisuus jne.), sigman kokojen suora vertailu on mahdotonta , koska keskihajonta on nimetty arvo, joka ilmaistaan absoluuttisina lukuina. Käytä näissä tapauksissa variaatiokerroin (CV) , joka on suhteellinen arvo: keskihajonnan prosentuaalinen suhde aritmeettiseen keskiarvoon.

Variaatiokerroin lasketaan kaavalla:

Mitä suurempi variaatiokerroin , mitä suurempi tämän sarjan vaihtelu on. Uskotaan, että yli 30 %:n variaatiokerroin osoittaa populaation laadullisen heterogeenisyyden.

Standardipoikkeama(synonyymit: keskihajonta, keskihajonta, neliöpoikkeama; liittyvät termit: keskihajonta, standardi leviäminen) - todennäköisyysteoriassa ja tilastoissa yleisin indikaattori satunnaismuuttujan arvojen hajoamisesta suhteessa sen matemaattiseen odotukseen. Rajoitetuille arvonäytteiden ryhmille sen sijaan matemaattinen odotus käytetään otosjoukon aritmeettista keskiarvoa.

Tietosanakirja YouTube

1 / 5

Keskihajonta mitataan itse mittayksiköissä Satunnaismuuttuja ja sitä käytetään laskettaessa aritmeettisen keskiarvon keskivirhettä, muodostettaessa luottamusväliä, testattaessa tilastollisesti hypoteeseja, mitattaessa satunnaismuuttujien välistä lineaarista suhdetta. Määritetään satunnaismuuttujan varianssin neliöjuureksi.

Vakiopoikkeama:

s = n n − 1 σ 2 = 1 n − 1 ∑ i = 1 n (x i − x ¯) 2 ; (\displaystyle s=(\sqrt ((\frac (n)(n-1))\sigma ^(2)))=(\sqrt ((\frac (1)(n-1))\sum _( i=1)^(n)\vasen(x_(i)-(\bar (x))\oikea)^(2)));)

Huomautus: Hyvin usein MSD:n (Root Mean Square Deviation) ja STD:n (Standard Deviation) nimissä on eroja kaavoineen. Esimerkiksi Python-ohjelmointikielen numPy-moduulissa std()-funktio on kuvattu "standardipoikkeamaksi", kun taas kaava heijastaa keskihajontaa (jako näytteen juurella). Excelissä STANDARDEVAL()-funktio on erilainen (jako n-1:n juurella).

Standardipoikkeama(arvio satunnaismuuttujan keskihajonnasta x suhteessa sen matemaattiseen odotukseen, joka perustuu sen varianssin puolueettomaan arvioon) s (\displaystyle s):

σ = 1 n ∑ i = 1 n (x i − x ¯) 2 . (\displaystyle \sigma =(\sqrt ((\frac (1)(n))\sum _(i=1)^(n)\left(x_(i)-(\bar (x))\oikea) ^(2))).)

Missä σ 2 (\displaystyle \sigma ^(2))- dispersio; x i (\displaystyle x_(i)) - i valinnan th elementti; n (\displaystyle n)- otoskoko; - otoksen aritmeettinen keskiarvo:

x ¯ = 1 n ∑ i = 1 n x i = 1 n (x 1 + … + x n). (\displaystyle (\bar (x))=(\frac (1)(n))\sum _(i=1)^(n)x_(i)=(\frac (1)(n))(x_ (1)+\lpisteet +x_(n)).)

On huomattava, että molemmat arviot ovat puolueellisia. Yleisessä tapauksessa on mahdotonta muodostaa puolueetonta arviota. Puolueettomaan varianssiestimaattiin perustuva arvio on kuitenkin johdonmukainen.

Standardin GOST R 8.736-2011 mukaisesti standardipoikkeama lasketaan käyttämällä tämän osan toista kaavaa. Tarkista tulokset.

Kolmen sigman sääntö

Kolmen sigman sääntö (3 σ (\displaystyle 3\sigma)) - lähes kaikki normaalijakauman satunnaismuuttujan arvot ovat välissä (x ¯ − 3 σ ; x ¯ + 3 σ) (\displaystyle \left((\bar (x))-3\sigma ;(\bar (x))+3\sigma \oikea)). Tarkemmin sanottuna - noin todennäköisyydellä 0,9973, normaalijakauman satunnaismuuttujan arvo on määritetyllä välillä (edellyttäen, että arvo x ¯ (\displaystyle (\bar (x))) totta, eikä saatu näytekäsittelyn tuloksena).

Jos todellinen arvo x ¯ (\displaystyle (\bar (x))) on tuntematon, sinun ei pitäisi käyttää σ (\displaystyle \sigma ), A s. Siten kolmen sigman sääntö muuttuu kolmen sigman säännöksi s .

Keskihajonnan arvon tulkinta

Suurempi keskihajonnan arvo osoittaa suuremman arvojen leviämisen esitetyssä joukossa joukon keskiarvolla; vastaavasti pienempi arvo osoittaa, että joukon arvot on ryhmitelty keskiarvon ympärille.

Meillä on esimerkiksi kolme numerojoukkoa: (0, 0, 14, 14), (0, 6, 8, 14) ja (6, 6, 8, 8). Kaikilla kolmella joukolla on keskiarvot, jotka ovat yhtä suuria kuin 7, ja standardipoikkeamat vastaavasti 7, 5 ja 1. Viimeisellä joukolla on pieni keskihajonta, koska joukon arvot on ryhmitelty keskiarvon ympärille; ensimmäisessä sarjassa on eniten hyvin tärkeä keskihajonta - joukon arvot poikkeavat suuresti keskiarvosta.

Yleisesti ottaen standardipoikkeamaa voidaan pitää epävarmuuden mittana. Esimerkiksi fysiikassa keskihajontaa käytetään jonkin suuren peräkkäisten mittausten sarjan virheen määrittämiseen. Tämä arvo on erittäin tärkeä määritettäessä tutkittavan ilmiön uskottavuutta verrattuna teorian ennustamaan arvoon: jos mittausten keskiarvo poikkeaa suuresti teorian ennustamista arvoista (suuri keskihajonta), sitten saadut arvot tai menetelmä niiden saamiseksi on tarkistettava uudelleen. tunnistaa portfolioriskin kanssa.

Ilmasto

Oletetaan, että kahdessa kaupungissa on sama keskimääräinen vuorokauden enimmäislämpötila, mutta toinen sijaitsee rannikolla ja toinen tasangolla. Tiedetään, että rannikolla sijaitsevissa kaupungeissa on monia erilaisia maksimipäivälämpötiloja, jotka ovat alhaisempia kuin sisämaassa sijaitsevissa kaupungeissa. Siksi rannikkokaupungin vuorokausilämpötilojen keskihajonta on pienempi kuin toisen kaupungin huolimatta siitä, että niiden keskiarvo on sama, mikä käytännössä tarkoittaa, että todennäköisyys, että Maksimilämpötila kunkin päivän ilma eroaa voimakkaammin keskiarvosta, korkeampi mantereen sisällä sijaitsevan kaupungin osalta.

Urheilu

Oletetaan, että on olemassa useita jalkapallojoukkueita, jotka on luokiteltu joillakin parametreilla, esimerkiksi tehtyjen ja päästettyjen maalien lukumäärällä, maalintekomahdollisuuksilla jne. On todennäköistä, että tämän ryhmän parhaalla joukkueella on paremmat arvot useammalla parametrilla. Mitä pienempi joukkueen keskihajonta kullekin esitetylle parametrille on, sitä ennakoitavampi on joukkueen tulos; tällaiset joukkueet ovat tasapainoisia. Toisaalta suuren keskihajonnan omaavan joukkueen tulosta on vaikea ennustaa, mikä puolestaan selittyy epätasapainolla, esimerkiksi vahvalla puolustuksella mutta heikolla hyökkäyksellä.

Joukkueparametrien keskihajonnan avulla voidaan tavalla tai toisella ennustaa kahden joukkueen välisen ottelun tulos arvioimalla vahvuuksia ja heikkoja puolia komennot ja siten valitut taistelutavat.

Yksi tilastollisen analyysin tärkeimmistä työkaluista on keskihajonnan laskenta. Tämän indikaattorin avulla voit arvioida otoksen tai populaation keskihajonnan. Opitaan käyttämään keskihajonnan kaavaa Excelissä.

Selvitetään heti, mikä keskihajonna on ja miltä sen kaava näyttää. Tämä arvo on keskiarvon neliöjuuri aritmeettinen luku sarjan kaikkien arvojen ja niiden aritmeettisen keskiarvon välisen eron neliöt. Tälle indikaattorille on identtinen nimi - keskihajonta. Molemmat nimet ovat täysin samanarvoisia.

Mutta luonnollisesti Excelissä käyttäjän ei tarvitse laskea tätä, koska ohjelma tekee kaiken hänen puolestaan. Opitaan laskemaan keskihajonta Excelissä.

Laskenta Excelissä

Voit laskea määritetyn arvon Excelissä käyttämällä kahta erikoisfunktiota STDEV.V(otosjoukon perusteella) ja STDEV.G(perustuen yleiseen väestöön). Niiden toimintaperiaate on täysin sama, mutta niitä voidaan kutsua kolmella tavalla, joista keskustelemme alla.

Tapa 1: Ohjattu toimintotoiminto

Menetelmä 2: Kaavat-välilehti

Tapa 3: Syötä kaava manuaalisesti

On myös tapa, jolla sinun ei tarvitse kutsua argumenttiikkunaa ollenkaan. Tätä varten sinun on syötettävä kaava manuaalisesti.

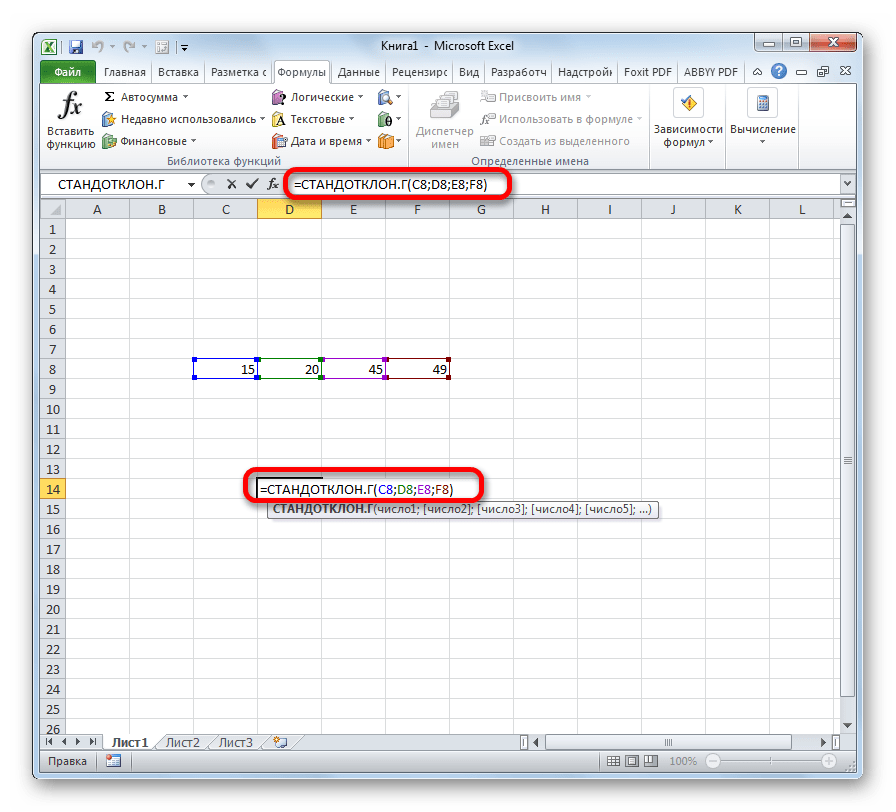
Kuten näet, mekanismi keskihajonnan laskemiseksi Excelissä on hyvin yksinkertainen. Käyttäjän tarvitsee vain syöttää numeroita populaatiosta tai viittauksia niitä sisältäviin soluihin. Kaikki laskelmat suorittaa ohjelma itse. On paljon vaikeampaa ymmärtää, mikä on laskettu indikaattori ja miten laskentatuloksia voidaan soveltaa käytännössä. Mutta tämän ymmärtäminen liittyy jo enemmän tilastoalaan kuin ohjelmiston kanssa työskentelyn oppimiseen.

Oppitunti nro 4

Aihe: "Kuvaustilastot. Ominaisuuksien monimuotoisuuden indikaattorit kokonaisuutena"

Tärkeimmät kriteerit ominaisuuden monimuotoisuudelle tilastollisessa perusjoukossa ovat: raja, amplitudi, keskihajonta, värähtelykerroin ja variaatiokerroin. Edellisellä oppitunnilla keskusteltiin siitä, että keskiarvot antavat vain yleisen ominaisuuden tutkittavalle ominaisuudelle aggregaatissa eivätkä ota huomioon sen yksittäisten muunnelmien arvoja: minimi- ja maksimiarvot, keskiarvon yläpuolella, alle keskimäärin jne.

Esimerkki. Kahden eri numerosarjan keskiarvot: -100; -20; 100; 20 ja 0,1; -0,2; 0.1 ovat täysin identtisiä ja samanarvoisiaNOIN.Näiden suhteellisten keskimääräisten sekvenssitietojen sironta-alueet ovat kuitenkin hyvin erilaisia.

Ominaisuuden monimuotoisuuden lueteltujen kriteerien määrittäminen tapahtuu ensisijaisesti ottaen huomioon sen arvo tilastollisen perusjoukon yksittäisissä elementeissä.

Indikaattorit piirteen vaihtelun mittaamiseksi ovat ehdoton Ja suhteellinen. Muutoksen absoluuttisia indikaattoreita ovat: vaihteluväli, raja, keskihajonta, hajonta. Variaatiokerroin ja värähtelykerroin viittaavat suhteellisiin variaatiomittauksiin.

Raja (lim) – Tämä on kriteeri, jonka määrittävät muunnelman ääriarvot variaatiosarjassa. Toisin sanoen tätä kriteeriä rajoittavat määritteen vähimmäis- ja enimmäisarvot:

Amplitudi (am) tai vaihteluväli - Tämä on ero äärimmäisten vaihtoehtojen välillä. Tämän kriteerin laskenta suoritetaan vähentämällä sen vähimmäisarvo attribuutin enimmäisarvosta, jonka avulla voimme arvioida vaihtoehdon hajontaasteen:

Rajan ja amplitudin haittana vaihtelukriteereinä on, että ne riippuvat täysin vaihtelusarjan ominaisuuden ääriarvoista. Tässä tapauksessa sarjan sisällä olevia attribuuttiarvojen vaihteluita ei oteta huomioon.

Täydellisen kuvauksen piirteen monimuotoisuudesta tilastollisessa populaatiossa tarjoaa keskihajonta(sigma), joka on yleinen mitta option poikkeamalle sen keskiarvosta. Standardipoikkeamaa kutsutaan usein keskihajonta.

Keskihajonta perustuu kunkin vaihtoehdon vertailuun tietyn perusjoukon aritmeettiseen keskiarvoon. Koska aggregaatissa on aina vaihtoehtoja sekä vähemmän että enemmän kuin se, poikkeamien summa merkillä "" kumotaan poikkeamien summalla merkillä "", ts. kaikkien poikkeamien summa on nolla. Erojen etumerkkien vaikutuksen välttämiseksi otetaan poikkeamat aritmeettisen keskiarvon neliöstä, ts. . Poikkeamien neliösumma ei ole nolla. Saadaksesi kertoimen, joka voi mitata vaihtelua, ota neliöiden summan keskiarvo - tätä arvoa kutsutaan varianssit:

Pohjimmiltaan dispersio on ominaisuuden yksittäisten arvojen poikkeamien keskimääräinen neliö sen keskiarvosta. Dispersio – keskihajonnan neliö.

Varianssi on mittasuure (nimetty). Joten jos lukusarjan muunnelmat ilmaistaan metreinä, niin varianssi antaa neliömetriä; jos vaihtoehdot ilmaistaan kilogrammoina, niin varianssi antaa tämän mittarin neliön (kg 2) jne.

Standardipoikkeama – Neliöjuuri dispersiosta:

, silloin kun lasketaan dispersiota ja keskihajontaa murtoluvun nimittäjässä, sen sijaan, ettätäytyy laittaa.

Keskihajonnan laskenta voidaan jakaa kuuteen vaiheeseen, jotka on suoritettava tietyssä järjestyksessä:

Keskihajonnan soveltaminen:

a) variaatiosarjojen vaihtelun arvioimiseen ja aritmeettisten keskiarvojen tyypillisyyden (representatiivisuuden) vertailemiseen. Tämä on tarpeen erotusdiagnoosissa määritettäessä oireiden vakautta.

b) rekonstruoida variaatiosarja, ts. sen taajuusvasteen palauttaminen kolme sigma sääntöä. Välillä (М±3σ) 99,7 % sarjan kaikista versioista sijaitsee välissä (М±2σ) - 95,5 % ja välillä (М±1σ) - 68,3 % riviversio(Kuva 1).

c) tunnistaa "ponnahdusikkunat".

d) määrittää normin ja patologian parametrit sigmaestimaateilla

e) laskea variaatiokerroin

f) laskea aritmeettisen keskiarvon keskimääräinen virhe.

Luonnehditaan mitä tahansa väestöä, jolla onnormaalijakauman tyyppi , riittää kun tietää kaksi parametria: aritmeettinen keskiarvo ja keskihajonta.

Kuva 1. Kolmen sigman sääntö

Esimerkki.

Pediatriassa keskihajonnan avulla arvioidaan lasten fyysistä kehitystä vertaamalla tietyn lapsen tietoja vastaaviin standardiindikaattoreihin. Standardiksi otetaan terveiden lasten fyysisen kehityksen aritmeettinen keskiarvo. Indikaattorien vertailu standardeihin tehdään erityisillä taulukoilla, joissa standardit on annettu niitä vastaavien sigma-asteikkojen kanssa. Uskotaan, että jos lapsen fyysisen kehityksen indikaattori on standardin (aritmeettinen keskiarvo) ±σ sisällä, niin lapsen fyysinen kehitys (tämän indikaattorin mukaan) vastaa normia. Jos osoitin on standardin ±2σ sisällä, on pieni poikkeama normista. Jos indikaattori ylittää nämä rajat, lapsen fyysinen kehitys eroaa jyrkästi normista (patologia on mahdollista).

Absoluuttisilla arvoilla ilmaistujen variaatioindikaattoreiden lisäksi tilastotutkimuksessa käytetään suhteellisilla arvoilla ilmaistuja variaatioindikaattoreita. Värähtelykerroin - tämä on vaihtelualueen suhde ominaisuuden keskiarvoon. Variaatiokerroin - tämä on keskihajonnan suhde ominaisuuden keskiarvoon. Tyypillisesti nämä arvot ilmaistaan prosentteina.

Kaavat suhteellisten vaihteluindikaattoreiden laskemiseksi:

Yllä olevista kaavoista on selvää, että mitä suurempi kerroin V on lähempänä nollaa, sitä pienempi on ominaisuuden arvojen vaihtelu. Sitä enemmän V, sitä vaihtelevampi merkki.

Tilastokäytännössä käytetään useimmiten variaatiokerrointa. Sitä ei käytetä vain vaihtelun vertailevaan arviointiin, vaan myös populaation homogeenisuuden karakterisointiin. Populaatio katsotaan homogeeniseksi, jos variaatiokerroin ei ylitä 33 % (lähellä normaalijakaumia). Aritmeettisesti σ:n ja aritmeettisen keskiarvon suhde neutraloi näiden ominaisuuksien itseisarvon vaikutuksen, ja prosenttisuhde tekee variaatiokertoimesta dimensiottoman (nimettömän) arvon.

Tuloksena oleva variaatiokertoimen arvo arvioidaan piirteen monimuotoisuusasteen likimääräisten asteiden mukaan:

Heikko - jopa 10%

Keskiarvo - 10 - 20 %

Vahva - yli 20 %

Variaatiokertoimen käyttö on suositeltavaa tapauksissa, joissa on tarpeen verrata kooltaan ja mitoiltaan erilaisia ominaisuuksia.

Variaatiokertoimen ja muiden sirontakriteerien välinen ero on selvästi osoitettu esimerkki.

pöytä 1

Teollisuusyritysten työntekijöiden kokoonpano

Esimerkissä annettujen tilastollisten ominaisuuksien perusteella voimme tehdä johtopäätöksen yrityksen työntekijöiden ikäjakauman ja koulutustason suhteellisesta homogeenisuudesta, kun otetaan huomioon tutkittavan joukon alhainen ammatillinen vakaus. On helppo nähdä, että yritys arvioida näitä yhteiskunnallisia suuntauksia keskihajonnan perusteella johtaisi virheelliseen johtopäätökseen, ja yritys verrata kirjanpidon ominaisuuksia "työkokemus" ja "ikä" kirjanpitoindikaattoriin "koulutus" olisi yleensä virheellinen näiden ominaisuuksien heterogeenisyyden vuoksi.

Mediaani ja prosenttipisteet

Järjestysjakaumissa, joissa sarjan keskikohdan kriteeri on mediaani, keskihajonta ja hajonta eivät voi toimia muunnelman hajonnan ominaisuuksina.

Sama pätee avoimiin variaatiosarjoihin. Tämä seikka johtuu siitä, että poikkeamat, joista varianssi ja σ lasketaan, mitataan aritmeettisesta keskiarvosta, jota ei lasketa avoimissa variaatiosarjoissa ja kvalitatiivisten ominaisuuksien jakaumien sarjoissa. Siksi jakaumien pakattuun kuvaukseen käytetään toista sirontaparametria - kvantiili(synonyymi - "prosenttipiste"), sopii kuvaamaan laadullisia ja määrällisiä ominaisuuksia niiden jakautumisen missä tahansa muodossa. Tätä parametria voidaan käyttää myös kvantitatiivisten ominaisuuksien muuntamiseen laadullisiksi. Tässä tapauksessa tällaiset arvosanat määritetään sen mukaan, mitä kvantiilin järjestystä tietty vaihtoehto vastaa.

Biolääketieteellisen tutkimuksen käytännössä käytetään useimmiten seuraavia kvantiileja:

– mediaani;

, – kvartiilit (neljännekset), missä – alempi kvartiili, – ylin kvartiili.

Kvantiilit jakavat vaihtelusarjan mahdollisten muutosten alueen tiettyihin intervalleihin. Mediaani (kvantiili) on vaihtoehto, joka on variaatiosarjan keskellä ja jakaa tämän sarjan kahtia kahteen yhtä suureen osaan ( 0,5 Ja 0,5 ). Kvartiili jakaa sarjan neljään osaan: ensimmäinen osa (alempi kvartiili) on optio, joka erottaa optiot, joiden numeeriset arvot eivät ylitä 25 % tietyn sarjan suurimmasta mahdollisesta; kvartiili erottaa optiot, joiden numeerinen arvo on jopa 50 % mahdollisesta enimmäismäärästä. Ylempi kvartiili () erottaa vaihtoehdot 75 %:iin asti maksimiarvoista.

Epäsymmetrisen jakauman tapauksessa muuttuja suhteessa aritmeettiseen keskiarvoon, sen karakterisoimiseen käytetään mediaania ja kvartiileja. Tässä tapauksessa käytetään seuraavaa keskiarvon näyttötapaa - meh (;). Esimerkiksi, tutkittavalla ominaisuudella – "ajanjaksolla, jolloin lapsi alkoi kävellä itsenäisesti" – on epäsymmetrinen jakautuminen tutkimusryhmässä. Samaan aikaan alempi kvartiili () vastaa kävelyn alkua - 9,5 kuukautta, mediaani - 11 kuukautta, ylempi kvartiili () - 12 kuukautta. Vastaavasti määritetyn attribuutin keskimääräisen trendin ominaisuus esitetään muodossa 11 (9,5; 12) kuukautta.

Tutkimustulosten tilastollisen merkitsevyyden arviointi

Tiedon tilastollinen merkitsevyys ymmärretään sen asteena, missä määrin se vastaa näytettävää todellisuutta, ts. Tilastollisesti merkitseviä tietoja ovat tiedot, jotka eivät vääristä ja kuvastavat oikein objektiivista todellisuutta.

Tutkimustulosten tilastollisen merkittävyyden arvioiminen tarkoittaa sen määrittämistä, millä todennäköisyydellä otosjoukosta saadut tulokset on mahdollista siirtää koko perusjoukolle. Tilastollisen merkittävyyden arvioiminen on välttämätöntä, jotta voidaan ymmärtää, kuinka paljon ilmiöstä voidaan arvioida ilmiötä kokonaisuutena ja sen malleja.

Tutkimustulosten tilastollisen merkitsevyyden arviointi koostuu seuraavista:

1. edustavuusvirheet (keskiarvojen ja suhteellisten arvojen virheet) - m;

2. keskimääräisten tai suhteellisten arvojen luottamusrajat;

3. keskimääräisten tai suhteellisten arvojen eron luotettavuus kriteerin mukaan t.

Aritmeettisen keskiarvon standardivirhe tai edustavuusvirhe luonnehtii keskiarvon vaihtelua. On huomattava, että mitä suurempi otoskoko on, sitä pienempi on keskiarvojen hajonta. Keskiarvon keskivirhe lasketaan kaavalla:

Nykyaikaisessa tieteellisessä kirjallisuudessa aritmeettinen keskiarvo kirjoitetaan edustavuusvirheen kanssa:

tai yhdessä keskihajonnan kanssa:

Tarkastellaan esimerkiksi tietoja maan 1 500 kaupunkiklinikasta (yleinen väestö). Keskimääräinen potilasmäärä klinikalla on 18 150 henkilöä. Satunnainen valinta 10 % paikoista (150 klinikkaa) antaa keskimääräiseksi potilaiden lukumääräksi 20 051 henkilöä. Näytteenottovirhe, joka johtuu ilmeisesti siitä, että kaikki 1500 klinikkaa eivät olleet mukana otoksessa, on yhtä suuri kuin näiden keskiarvojen erotus - yleinen keskiarvo ( M geeni) ja näytteen keskiarvo ( M valittu). Jos muodostamme populaatiostamme toisen samankokoisen otoksen, se antaa erilaisen virhearvon. Kaikki nämä näytteenottovälineet, riittävän suurilla näytteillä, jakautuvat normaalisti yleisen keskiarvon ympärille riittävän suurella määrällä otoksen toistoja samasta määrästä esineitä yleisestä populaatiosta. Keskiarvon standardivirhe m- tämä on väistämätön näytekeskiarvojen leviäminen yleisen keskiarvon ympärille.

Siinä tapauksessa, että tutkimustulokset esitetään suhteellisina määrinä (esimerkiksi prosentteina) - laskettu murto-osan standardivirhe:

missä P on indikaattori %, n on havaintojen lukumäärä.

Tulos näytetään muodossa (P ± m) %. Esimerkiksi, toipumisprosentti potilailla oli (95,2±2,5) %.

Siinä tapauksessa, että väestön elementtien lukumäärä, silloin kun lasketaan keskiarvon ja murtoluvun keskivirheitä murto-osan nimittäjässä, sen sijaan, ettätäytyy laittaa.

Normaalijakaumassa (otoskeskiarvojakauma on normaali) tiedämme, mikä osa populaatiosta kuuluu mihin tahansa keskiarvon ympärillä olevaan väliin. Erityisesti:

Käytännössä ongelmana on, että yleisen perusjoukon ominaisuudet ovat meille tuntemattomia ja otos tehdään juuri niiden estimointia varten. Tämä tarkoittaa, että jos teemme samankokoisia näytteitä n yleisestä populaatiosta, niin 68,3 %:ssa tapauksista väli sisältää arvon M(95,5 %:ssa tapauksista se tulee väliin ja 99,7 %:ssa – intervalliin).

Koska todellisuudessa otetaan vain yksi näyte, tämä väite on muotoiltu todennäköisyydellä: 68,3 %:n todennäköisyydellä määritteen keskiarvo perusjoukossa on välissä, todennäköisyydellä 95,5 %. - välissä jne.

Käytännössä näytearvon ympärille rakennetaan intervalli siten, että tietyllä (riittävän suurella) todennäköisyydellä luottamustodennäköisyys -"kattaisi" tämän parametrin todellisen arvon yleisessä populaatiossa. Tätä väliä kutsutaan luottamusväli.

Luottamuksen todennäköisyysP – tämä on luottamusaste siihen, että luottamusväli todella sisältää perusjoukon parametrin todellisen (tuntemattoman) arvon.

Esimerkiksi jos luottamustodennäköisyys R on 90%, mikä tarkoittaa, että 90 näytettä 100:sta antaa oikean arvion perusjoukon parametrista. Vastaavasti virheen todennäköisyys, ts. otoksen yleisen keskiarvon virheellinen arvio on yhtä suuri prosentteina: . Tässä esimerkissä tämä tarkoittaa, että 10 näytettä 100:sta antaa väärän arvion.

Ilmeisesti luottamusaste (luottamustodennäköisyys) riippuu intervallin koosta: mitä leveämpi intervalli on, sitä suurempi on luottamus siihen, että populaation tuntematon arvo putoaa siihen. Käytännössä vähintään kaksinkertaista näytteenottovirhettä käytetään luomaan luottamusväli, joka antaa vähintään 95,5 %:n luotettavuuden.

Keskiarvojen ja suhteellisten arvojen luottamusrajojen määrittäminen antaa mahdollisuuden löytää niiden kaksi ääriarvoa - pienin mahdollinen ja suurin mahdollinen, joiden sisällä tutkittu indikaattori voi esiintyä koko väestössä. Tämän perusteella, luottamusrajat (tai luottamusväli)- nämä ovat keskimääräisten tai suhteellisten arvojen rajoja, joiden ylittämisen todennäköisyys on satunnaisten vaihtelujen vuoksi merkityksetön.

Luottamusväli voidaan kirjoittaa uudelleen muotoon: , missä t– luottamuskriteeri.

Perusjoukon aritmeettisen keskiarvon luottamusrajat määritetään kaavalla:

M geeni = M valitse + t m M

suhteelliselle arvolle:

R geeni = P valitse + t m R

Missä M geeni Ja R geeni- keskimääräisten ja suhteellisten arvojen arvot väestölle; M valitse Ja R valitse- näytepopulaatiosta saatujen keskiarvojen ja suhteellisten arvojen arvot; m M Ja m P- keskiarvojen ja suhteellisten arvojen virheet; t- luottamuskriteeri (tarkkuuskriteeri, joka määritetään tutkimusta suunniteltaessa ja voi olla 2 tai 3); t m- tämä on luottamusväli tai Δ - näytetutkimuksessa saadun indikaattorin maksimivirhe.

On huomattava, että kriteerin arvo t liittyy jossain määrin virheettömän ennusteen todennäköisyyteen (p), prosentteina ilmaistuna. Sen valitsee tutkija itse, ohjaten tarve saada tulos vaaditulla tarkkuudella. Siten 95,5 %:n virheettömän ennusteen todennäköisyydelle kriteerin arvo t on 2, 99,7 % - 3.

Annetut luottamusvälin estimaatit ovat hyväksyttäviä vain tilastollisille populaatioille, joissa on yli 30 havaintoa, pienemmällä populaatiokoolla (pienet otokset) t-kriteerin määrittämiseen käytetään erityisiä taulukoita. Näissä taulukoissa haluttu arvo sijaitsee populaation kokoa vastaavan viivan leikkauskohdassa (n-1), ja sarake, joka vastaa tutkijan valitseman virheettömän ennusteen todennäköisyystasoa (95,5 %; 99,7 %). Lääketieteellisessä tutkimuksessa luotettavuusrajoja määritettäessä mille tahansa indikaattorille virheettömän ennusteen todennäköisyys on 95,5 % tai enemmän. Tämä tarkoittaa, että otosjoukosta saadun indikaattorin arvon tulee löytyä yleisjoukosta vähintään 95,5 %:ssa tapauksista.

Kysymyksiä oppitunnin aiheesta:

Ominaisuuksien monimuotoisuuden indikaattoreiden merkitys tilastoväestössä.

Yleiset luonteenpiirteet absoluuttiset indikaattorit muunnelmat.

Keskihajonta, laskenta, soveltaminen.

Suhteelliset vaihtelumitat.

Mediaani, kvartiilipisteet.

Opintotulosten tilastollisen merkitsevyyden arviointi.

Aritmeettisen keskiarvon keskivirhe, laskentakaava, käyttöesimerkki.

Suhteen ja sen keskivirheen laskeminen.

Luottamustodennäköisyyden käsite, esimerkki käytöstä.

10. Luottamusvälin käsite, sen soveltaminen.

Aiheen testitehtävät vakiovastauksilla:

1. ABSOLUUTTISET VAIHTO-INDIKAATTORIT, JOITA KATSO

1) variaatiokerroin

2) värähtelykerroin

4) mediaani

2. SUHTEELLISET VAIHTO-INDIKAATTORIT RELATE

1) dispersio

4) variaatiokerroin

3. KRITEERI, JOKA MÄÄRITÄÄN VARIAATIOSARJAN VAIHTOEHTOJEN ÄRIARVOJEN

2) amplitudi

3) dispersio

4) variaatiokerroin

4. Äärimmäisten vaihtoehtojen EROTUS ON

2) amplitudi

3) keskihajonta

4) variaatiokerroin

5. OMINAISUUDEN YKSITTÄISTEN ARVOJEN KESKIMÄÄRÄISTÄ POIKKEAMIEN KESKIMÄÄRÄINEN neliö ON

1) värähtelykerroin

2) mediaani

3) dispersio

6. VAIHTO-ASteikon SUHDE HAHMEN KESKIMÄÄRÄISEEN ARVOON ON

1) variaatiokerroin

2) keskihajonta

4) värähtelykerroin

7. KESKIMÄÄRÄISEN NELIÖPOIKKAAN SUHDE OMINAISUUDEN KESKIMÄÄRÄISEEN ARVOON ON

1) dispersio

2) variaatiokerroin

3) värähtelykerroin

4) amplitudi

8. VAIHTOEHTO, JOKA ON KESKELMÄSSÄ VARIATIOSARJAA JA JAKAA SEN KAHEEN TASASUUREEN OSAAN ON

1) mediaani

3) amplitudi

9. LÄÄKETIETEELLISSÄ TUTKIMUKSEESSA MÄÄRITETTÄESSÄ LUOTTAMISRAJAA JOHDANKAAN INDIKAATTORILLE, VIRHEETTÖMÄN ENNUSTUKSEN TODENNÄKÖISYYS HYVÄKSYTÄÄN

10. JOS 90 NÄYTTÖÄ 100:STA ANTAA OIKEA ARVIOIN PARAMETRISTA POPULAATIOSSA, TÄMÄ TARKAA, ETTÄ LUOTTAVUUS TODENNÄKÖISYYS P YHTÄ SUURI

11. JOS 10 NÄYTTÖÄ 100:STA ANTAA VÄÄRÄN ARVIOIN, VIRHEEN TODENNÄKÖISYYS ON

12. KESKIARVOJEN TAI SUHTEISTEN ARVOJEN RAJAT, JOIDEN YLIMÄÄN SATUNNAISISTA VÄRINNÖistä ON PIENI TODENNÄKÖISYYS – TÄMÄ ON

1) luottamusväli

2) amplitudi

4) variaatiokerroin

13. PIENÄ OOTANNEKSI PIDÄÄN SEKÄ KANSSA, JOSSA

1) n on pienempi tai yhtä suuri kuin 100

2) n on pienempi tai yhtä suuri kuin 30

3) n on pienempi tai yhtä suuri kuin 40

4) n on lähellä nollaa

14. VIRHEETTÖMÄN ENNUSTEEN TODENNÄKÖISYYDEN 95 % ERIKOISARVO t ON

15. VIRHEETTÖMÄN ENNUSTEEN TODENNÄKÖISYYDEN 99 % EHDOTARVO t ON

16. LÄHELLÄ NORMAALIA OLEVIEN JAKELUJEN KÄYTTÖÖN VÄESTÖN KATSELLA ON HOMOGEENINEN, JOS VAIHTOKERROIN EI YLITÄ

17. VAIHTOEHTO, EROTTELUOPTIOT, JOIDEN NUMEROARVO EI YLITÄ 25 % TIETTYÄ SARJASTA MAHDOLLISISTA MAHDOLLISISTA – TÄMÄ ON

2) alempi kvartiili

3) ylempi kvartiili

4) kvartiili

18. TIETOA, JOKA EI VÄÄRÄ JA OIKEIN VASTAA OBJEKTIIVISTA TODELLISUUDESTA, KUTSUU

1) mahdotonta

2) yhtä mahdollista

3) luotettava

4) satunnainen

19. "KOLME SigMA" -SÄÄNNÖN MUKAAN, JOLLA OMINAISUUDET ON NORMAALI JAKELU
SIJOITTAAN

1) 68,3 % optio

Dispersio. Standardipoikkeama

Dispersio on kunkin attribuutin arvon neliöityjen poikkeamien aritmeettinen keskiarvo kokonaiskeskiarvosta. Lähdetiedoista riippuen varianssi voi olla painottamaton (yksinkertainen) tai painotettu.

Varianssi lasketaan seuraavilla kaavoilla:

· ryhmittämättömille tiedoille

· ryhmitellyille tiedoille

Painotetun varianssin laskentamenetelmä:

1. määrittää aritmeettinen painotettu keskiarvo

2. määritetään muunnelman poikkeamat keskiarvosta

3. neliötä kunkin vaihtoehdon poikkeama keskiarvosta

4. kerro poikkeamien neliöt painoilla (taajuuksilla)

5. Tee yhteenveto tuloksena olevista tuotteista

6. saatu määrä jaetaan asteikkojen summalla

Varianssin määrityskaava voidaan muuntaa seuraavaksi kaavaksi:

- yksinkertainen

Varianssin laskentamenettely on yksinkertainen:

1. määrittää aritmeettinen keskiarvo

2. neliöi aritmeettinen keskiarvo

3. neliöi jokainen rivin vaihtoehto

4. Etsi neliöiden summa -vaihtoehto

5. jaa neliöiden summa niiden lukumäärällä, ts. määrittää keskineliön

6. määritä ominaisuuden keskineliön ja keskiarvon neliön välinen ero

Myös painotetun varianssin määrityskaava voidaan muuntaa seuraavaksi kaavaksi:

nuo. dispersio on yhtä suuri kuin attribuutin neliöarvojen keskiarvon ja aritmeettisen keskiarvon neliön välinen ero. Käytettäessä muunnettua kaavaa eliminoituu lisämenettely ominaisuuden yksittäisten arvojen poikkeamien laskemiseksi x:stä ja poikkeamien pyöristämiseen liittyvä laskuvirhe poistetaan.

Dispersiolla on useita ominaisuuksia, joista osa helpottaa laskemista:

1) vakioarvon varianssi on nolla;

2) jos kaikkia attribuuttiarvojen muunnelmia vähennetään samalla numerolla, varianssi ei pienene;

3) jos kaikkia attribuuttiarvojen muunnelmia pienennetään saman verran (kertaa), niin varianssi pienenee kertoimella

Keskihajonta S- edustaa varianssin neliöjuurta:

· ryhmittämättömille tiedoille:

;

· variaatiosarjalle:

Vaihtelun vaihteluväli, lineaarinen keskiarvo ja keskihajonta on nimetty suureiksi. Niillä on samat mittayksiköt kuin yksittäisiä arvoja merkki.

Varianssi ja keskihajonta ovat yleisimmin käytetyt variaatiomitat. Tämä selittyy sillä, että ne sisältyvät useimpiin todennäköisyysteorian lauseisiin, jotka toimivat perustana matemaattiset tilastot. Lisäksi varianssi voidaan jakaa osatekijät, jonka avulla voidaan arvioida erilaisten tekijöiden vaikutusta, jotka aiheuttavat vaihtelua ominaisuudessa.

Pankkien variaatioindikaattoreiden laskeminen voittomarginaalin mukaan ryhmiteltynä on esitetty taulukossa.

Voiton määrä, miljoonaa ruplaa.	Pankkien lukumäärä	laskettuja indikaattoreita

3,7 - 4,6 (-)		4,15	8,30	-1,935	3,870	7,489
4,6 - 5,5		5,05	20,20	- 1,035	4,140	4,285
5,5 - 6,4		5,95	35,70	- 0,135	0,810	0,109
6,4 - 7,3		6,85	34,25	+0,765	3,825	2,926
7,3 - 8,2		7,75	23,25	+1,665	4,995	8,317
Kaikki yhteensä:			121,70		17,640	23,126

Keskimääräinen lineaarinen ja keskihajonta osoittavat, kuinka paljon ominaisuuden arvo vaihtelee keskimäärin yksiköiden ja tutkittavan perusjoukon välillä. Joten tässä tapauksessa keskimääräinen voiton vaihtelu on: keskimääräisen lineaarisen poikkeaman mukaan 0,882 miljoonaa ruplaa; keskihajonnan mukaan - 1,075 miljoonaa ruplaa. Keskihajonta on aina suurempi kuin keskimääräinen lineaarinen poikkeama. Jos ominaisuuden jakauma on lähellä normaalia, niin S:n ja d:n välillä on suhde: S=1,25d tai d=0,8S. Keskihajonta osoittaa, kuinka suurin osa perusjoukon yksiköistä sijaitsee suhteessa aritmeettiseen keskiarvoon. Jakauman muodosta riippumatta 75 attribuutin arvoa kuuluu väliin x 2S ja vähintään 89 kaikista arvoista väliin x 3S (P.L. Chebyshev'n lause).