Trigonometrisen funktion määrittelemätön integraali. Trigonometristen funktioiden integraalit

Tehtäviä tulee myös mm itsenäinen päätös, joihin näet vastaukset.

Integrandi voidaan muuntaa trigonometristen funktioiden tulosta summaksi

Tarkastellaan integraaleja, joissa integrandi on x:n ensimmäisen asteen sinien ja kosinien tulo kerrottuna eri tekijöillä, eli muodon integraaleja

Käyttämällä tunnettuja trigonometrisiä kaavoja

(2)
(3)
(4)
jokainen tuote muodon (31) integraaleissa voidaan muuttaa muotoon (31). algebrallinen summa ja integroi kaavojen avulla

(5)

(6)

Esimerkki 1. löytö

Ratkaisu. Kaavan (2) mukaan klo

Esimerkki 2. löytö trigonometrisen funktion integraali

Ratkaisu. Kaavan (3) mukaan klo

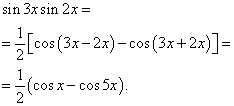
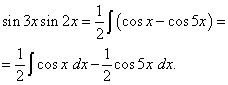
Esimerkki 3. löytö trigonometrisen funktion integraali

Ratkaisu. Kaavan (4) mukaan klo saamme seuraavan integrandin muunnoksen:

Kaavaa (6) soveltamalla saadaan

Integraali saman argumentin sinin ja kosinin potenssien tulosta

Tarkastellaan nyt funktioiden integraaleja, jotka ovat saman argumentin sinin ja kosinin potenssien tuloja, ts.

(7)

Erityistapauksissa yksi indikaattoreista ( m tai n) voi olla nolla.

Tällaisia ​​funktioita integroitaessa käytetään sitä, että kosinin parillinen potenssi voidaan ilmaista sinin kautta ja sinin differentiaali on yhtä suuri kuin cos x dx(tai jopa sinin potenssi voidaan ilmaista kosinina, ja kosinin differentiaali on yhtä suuri kuin - sin x dx ) .

On syytä erottaa kaksi tapausta: 1) vähintään yksi indikaattoreista m Ja n outo; 2) molemmat indikaattorit ovat parillisia.

Tapahtukoon ensimmäinen tapaus, nimittäin indikaattori n = 2k+ 1 - pariton. Sitten sen huomioon ottaen

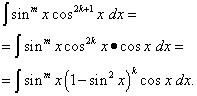
Integrandi esitetään siten, että yksi sen osa on vain sinin funktio ja toinen on sinin differentiaali. Nyt käytetään muuttujakorvaamista t= synti x ratkaisu pelkistyy integroimaan polynomin suhteessa t. Jos vain tutkinto m on outoa, he tekevät samoin eristäen syntitekijän x, joka ilmaisee loput integrandista cos-arvona x ja uskoa t=cos x. Tätä tekniikkaa voidaan käyttää myös silloin, kun integroimalla sinin ja kosinin osamääräpotenssit , Kun ainakin yksi indikaattoreista on pariton . Koko pointti on se sinin ja kosinin potenssien osamäärä on erikoistapaus heidän töitään : Kun trigonometrinen funktio on integrandin nimittäjässä, sen aste on negatiivinen. Mutta on myös yksityisiä tapauksia trigonometriset funktiot, kun niiden asteet ovat vain parillisia. Tietoja heistä - seuraavassa kappaleessa.

Jos molemmat indikaattorit m Ja n– jopa trigonometrisiä kaavoja käyttäen

pienennä sinin ja kosinin eksponenttia, minkä jälkeen saadaan samantyyppinen integraali kuin edellä. Siksi integraatiota tulisi jatkaa saman kaavan mukaan. Jos yksi parillisista eksponenteista on negatiivinen, eli otetaan huomioon sinin ja kosinin parillisten potenssien osamäärä, tämä kaavio ei sovellu . Tällöin käytetään muuttujan muutosta sen mukaan, kuinka integrandi voidaan muuntaa. Tällaista tapausta tarkastellaan seuraavassa kappaleessa.

Esimerkki 4. löytö trigonometrisen funktion integraali

Ratkaisu. Kosinieksponentti on pariton. Siksi kuvitellaan

t= synti x(Sitten dt=cos x dx ). Sitten saamme

Palaamme vanhaan muuttujaan, löydämme lopulta

Esimerkki 5. löytö trigonometrisen funktion integraali

.

Ratkaisu. Kosinieksponentti, kuten edellisessä esimerkissä, on pariton, mutta suurempi. Kuvitellaanpa

ja muuta muuttujaa t= synti x(Sitten dt=cos x dx ). Sitten saamme

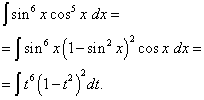
Avataan sulut

ja saamme

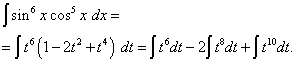
Palattuaan vanhaan muuttujaan, saamme ratkaisun

Esimerkki 6. löytö trigonometrisen funktion integraali

Ratkaisu. Sinin ja kosinin eksponentit ovat parillisia. Siksi muunnamme integrand-funktion seuraavasti:

Sitten saamme

Toisessa integraalissa muutamme muuttujaa, asetusta t= sin2 x. Sitten (1/2)dt= cos2 x dx . Siten,

Lopulta saamme

Muuttujan korvausmenetelmän käyttäminen

Muuttujan korvausmenetelmä integroitaessa trigonometrisia funktioita, sitä voidaan käyttää tapauksissa, joissa integrandi sisältää vain sinin tai vain kosinin, sinin ja kosinin tulon, jossa joko sini tai kosini on ensimmäisessä asteessa, tangentti tai kotangentti, sekä osamäärä jopa yhden ja saman argumentin sinin ja kosinin potenssit. Tässä tapauksessa on mahdollista suorittaa permutaatioita ei vain syntiä x = t ja syntiä x = t, mutta myös tg x = t ja ctg x = t .

Esimerkki 8. löytö trigonometrisen funktion integraali

.

Ratkaisu. Muutetaan muuttuja: , sitten . Tuloksena oleva integrandi voidaan integroida helposti integraalitaulukon avulla:

.

Esimerkki 9. löytö trigonometrisen funktion integraali

Ratkaisu. Muunnetaan tangentti sinin ja kosinin suhteeksi:

Muutetaan muuttuja: , sitten . Tuloksena oleva integrandi on pöydän integraali miinusmerkillä:

.

Palataksemme alkuperäiseen muuttujaan, saamme lopulta:

.

Esimerkki 10. löytö trigonometrisen funktion integraali

Ratkaisu. Muutetaan muuttuja: , sitten .

Muunnetaan integrandi soveltamaan trigonometristä identiteettiä :

Muutamme muuttujaa unohtamatta laittaa miinusmerkkiä integraalin eteen (katso yllä, mikä on yhtä kuin dt). Seuraavaksi otamme huomioon integrandin ja integroimme taulukon mukaan:

Palataksemme alkuperäiseen muuttujaan, saamme lopulta:

.

Etsi itse trigonometrisen funktion integraali ja katso sitten ratkaisua

Universaali trigonometrinen substituutio

Universaali trigonometrinen substituutio voidaan käyttää tapauksissa, joissa integrandi ei kuulu edellisissä kappaleissa käsiteltyjen tapausten piiriin. Periaatteessa, kun sini tai kosini (tai molemmat) on murtoluvun nimittäjässä. On todistettu, että sini ja kosini voidaan korvata toisella lausekkeella, joka sisältää puolen alkuperäisen kulman tangentin seuraavasti:

Mutta huomaa, että universaali trigonometrinen substituutio sisältää usein melko monimutkaisia ​​algebrallisia muunnoksia, joten sitä on parasta käyttää, kun mikään muu menetelmä ei toimi. Katsotaanpa esimerkkejä, joissa universaalin trigonometrisen substituution kanssa käytetään substituutiota differentiaalimerkin alla ja epämääräisten kertoimien menetelmää.

Esimerkki 12. löytö trigonometrisen funktion integraali

.

Ratkaisu. Ratkaisu. Hyödynnetään universaali trigonometrinen substituutio. Sitten
.

Kerrotaan osoittajan ja nimittäjän murtoluvut luvulla, otetaan kaksi pois ja asetetaan integraalimerkin eteen. Sitten

Trigonometriset peruskaavat ja peruskorvaukset esitetään. Menetelmät trigonometristen funktioiden integroimiseksi on hahmoteltu - integrointi rationaalisia toimintoja, sin x:n ja cos x:n potenssifunktioiden tulo, polynomin, eksponentiaalin ja sinin tai kosinin tulo, käänteisten trigonometristen funktioiden integrointi. Tämä vaikuttaa epästandardeihin menetelmiin.

Vakiomenetelmät trigonometristen funktioiden integroimiseksi

Yleinen lähestymistapa

Ensin integrandi on tarvittaessa muutettava siten, että trigonometriset funktiot riippuvat yhdestä argumentista, joka on sama kuin integraatiomuuttuja.

Esimerkiksi, jos integrandi riippuu synti(x+a) Ja cos(x+b), sinun tulee suorittaa muunnos:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + synti ( x+a ) synti (b-a).
Korvaa sitten z = x+a. Tämän seurauksena trigonometriset funktiot riippuvat vain integrointimuuttujasta z.

Kun trigonometriset funktiot riippuvat yhdestä argumentista, joka osuu yhteen integrointimuuttujan kanssa (oletetaan, että se on z), eli integrandi koostuu vain funktioista, kuten sin z, cos z, tg z, ctg z, sinun on suoritettava vaihto
.
Tällainen substituutio johtaa rationaalisten tai irrationaalisten funktioiden integrointiin (jos on juuria) ja mahdollistaa integraalin laskemisen, jos se on integroitu alkeisfunktioihin.

Voit kuitenkin usein löytää muita menetelmiä, joiden avulla voit laskea integraalin enemmän lyhyt tie, joka perustuu integrandin ominaisuuksiin. Alla on yhteenveto tärkeimmistä tällaisista menetelmistä.

Menetelmät sin x:n ja cos x:n rationaalisten funktioiden integroimiseksi

Rationaaliset funktiot alkaen synti x Ja cos x ovat funktioita, jotka on muodostettu synti x, cos x ja kaikki vakiot, jotka käyttävät yhteen-, vähennys-, kerto-, jakolasku- ja kokonaislukupotenssiin korottamista. Ne on nimetty seuraavasti: R (sin x, cos x). Tämä voi sisältää myös tangentit ja kotangentit, koska ne muodostetaan jakamalla sini kosinilla ja päinvastoin.
Rationaalisten funktioiden integraaleilla on muoto:
.

Menetelmät rationaalisten trigonometristen funktioiden integroimiseksi ovat seuraavat.
1) Korvaus johtaa aina integraaliin rationaalinen murto-osa. Joissakin tapauksissa on kuitenkin korvauksia (nämä on esitetty alla), jotka johtavat lyhyempiin laskelmiin.
2) Jos R (sin x, cos x) cos x → - cos x synti x.
3) Jos R (sin x, cos x) kerrottuna -1:llä vaihdettaessa sin x → - sin x, niin substituutio t = cos x.
4) Jos R (sin x, cos x) ei muutu kuin samanaikaisen vaihdon yhteydessä cos x → - cos x, Ja sin x → - sin x, niin substituutio t = tg x tai t = ctg x.

Esimerkkejä:
, , .

Cos x:n ja sin x:n potenssifunktioiden tulo

Lomakkeen integraalit

ovat rationaalisten trigonometristen funktioiden integraaleja. Siksi niihin voidaan soveltaa edellisessä osassa esitettyjä menetelmiä. Tällaisten integraalien erityispiirteisiin perustuvia menetelmiä käsitellään alla.

Jos m ja n - rationaalisia lukuja, sitten yksi substituutioista t = synti x tai t = cos x integraali pelkistetään differentiaalibinomiaalin integraaliksi.

Jos m ja n ovat kokonaislukuja, integrointi suoritetaan pelkistyskaavojen avulla:

;
;
;
.

Esimerkki:
.

Polynomin ja sinin tai kosinin tulon integraalit

Lomakkeen integraalit:
, ,
missä P(x) on x:n polynomi, integroidaan osilla. Tämä antaa seuraavat kaavat:

;
.

Esimerkkejä:
, .

Polynomin, eksponentiaalin ja sinin tai kosinin tulon integraalit

Lomakkeen integraalit:
, ,
jossa P(x) on polynomi x:ssä, integroitu Eulerin kaavalla
e iax = cos ax + isin ax(jossa i 2 = - 1 ).
Tätä varten laske integraali edellisessä kappaleessa kuvatulla menetelmällä
.
Erottamalla reaali- ja imaginaariosa tuloksesta saadaan alkuperäiset integraalit.

Esimerkki:
.

Epätyypilliset menetelmät trigonometristen funktioiden integroimiseksi

Alla on joukko epätyypillisiä menetelmiä, joiden avulla voit suorittaa tai yksinkertaistaa trigonometristen funktioiden integrointia.

Riippuvuus (a sin x + b cos x)

Jos integrandi riippuu vain a sin x + b cos x, niin on hyödyllistä käyttää kaavaa:
,
Missä .

Esimerkiksi

Murtolukujen erottaminen sinistä ja kosineista yksinkertaisemmiksi murtoiksi

Harkitse integraalia
.
Yksinkertaisin integrointimenetelmä on jakaa murto yksinkertaisemmiksi muunnolla:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Ensimmäisen asteen murto-osien integrointi

klo integraalilaskenta
,
on kätevää eristää murto-osan kokonaislukuosa ja nimittäjän derivaatta
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)′ .
Vakiot A ja B saadaan vertaamalla vasenta ja oikeaa puolta.

Viitteet:
N.M. Gunther, R.O. Kuzmin, Korkeamman matematiikan tehtäväkokoelma, "Lan", 2003.

Rationaalisten funktioiden integroimiseksi muotoa R(sin x, cos x) käytetään substituutiota, jota kutsutaan universaaliksi trigonometriseksi substituutioksi. Sitten . Universaali trigonometrinen korvaaminen johtaa usein suuriin laskelmiin. Siksi, aina kun mahdollista, käytä seuraavia korvauksia.

Trigonometrisista funktioista rationaalisesti riippuvaisten funktioiden integrointi

Muunnetaan trigonometristen funktioiden tulo niiden summaksi kaavoilla:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

Esimerkkejä
1. Laske integraali ∫ cos 4 x·sin 3 xdx .
Teemme korvauksen cos(x)=t. Sitten ∫ cos 4 x sin 3 xdx =
2. Laske integraali.
Tehdään korvaus sin x=t , saamme

Integrointilausekkeet muotoa R(sinx, cosx)

Esimerkki nro 1. Laske integraalit:

Ratkaisu.
a) Muodon R(sinx, cosx) lausekkeiden integraatiot, joissa R on sin x:n ja cos x:n rationaalinen funktio, muunnetaan rationaalisten funktioiden integraaleiksi käyttämällä universaalia trigonometristä substituutiota tg(x/2) = t.
Sitten meillä on

• Jos yhtälö R(-sin x, cos x) = -R(sin x, cos x)dx täyttyy, käytetään substituutiota cos x = t.
• Jos yhtälö R(sin x, -cos x) = -R(sin x, cos x)dx pätee, niin substituutio sin x = t.
• Jos yhtälö R(-sin x, -cos x) = R(sin x, cos x)dx pätee, niin substituutio tgx = t tai ctg x = t.

Käytännössä on usein tarpeen laskea transsendenttisten funktioiden integraalit, jotka sisältävät trigonometrisia funktioita. Osana tätä materiaalia kuvataan tärkeimmät integrointifunktioiden tyypit ja näytetään, millä menetelmillä ne voidaan integroida.

Integroi sini, kosini, tangentti ja kotangentti

Aloitetaan menetelmillä integroida trigonometriset perusfunktiot - sin, cos, t g, c t g. Antiderivaatataulukon avulla kirjoitetaan heti, että ∫ sin x d x = - cos x + C ja ∫ cos x d x = sin x + C.

Laskeaksesi funktioiden t g ja c t g epämääräiset integraalit, voit käyttää differentiaalimerkkiä:

∫ t g x d x = ∫ sin x cos x d x = d (cos x) = - sin x d x = = - ∫ d (cos x) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d (sin x) = cos x d x = = ∫ d (sin x) sin x = ln sin x + C

Kuinka saimme antiderivaatataulukosta otetut kaavat ∫ d x sin x = ln 1 - cos x sin x + C ja ∫ d x cos x = ln 1 + sin x cos x + C? Selitäkäämme vain yksi tapaus, koska toinen on selkeä analogisesti.

Korvausmenetelmää käyttämällä kirjoitamme:

∫ d x sin x = sin x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2

Tässä meidän on integroitava irrationaalinen funktio. Käytämme samaa korvausmenetelmää:

∫ d t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = = ∫ - z d z z 1 - z 2 1 - z 2 = 1 - z 2 1 - z 2 -1 ∫ d z (z - 1) (z +) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C

Nyt teemme käänteisen substituution z = 1 - t 2 ja t = sin x:

∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C

Analysoimme erikseen tapaukset integraaleilla, jotka sisältävät trigonometristen funktioiden potenssit, kuten ∫ sin n x d x, ∫ cos n x d x, ∫ d x sin n x, ∫ d x cos n x.

Voit lukea niiden laskemisesta oikein artikkelista, joka käsittelee integrointia toistuvuuskaavojen avulla. Jos tiedät kuinka nämä kaavat johdetaan, voit helposti ottaa integraalit, kuten ∫ sin n x · cos m x d x luonnollisella m:llä ja n:llä.

Jos meillä on trigonometristen funktioiden yhdistelmä polynomien tai eksponenttifunktioiden kanssa, ne on integroitava osittain. Suosittelemme lukemaan artikkelin, joka käsittelee integraalien ∫ P n (x) · sin (a x) d x , ∫ P n (x) · cos (a x) d x, ∫ e a · x · sin (a x) d x, ∫ e a etsimistä. · x · cos (a x) d x .

Vaikeimmat ongelmat ovat ne, joissa integrandi sisältää trigonometrisiä funktioita eri argumenteilla. Tätä varten sinun on käytettävä perustrigonometrian kaavoja, joten on suositeltavaa muistaa ne ulkoa tai pitää muistiinpanot käsillä.

Esimerkki 1

Laske funktion y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) antiderivaatojen joukko.

Ratkaisu

Käytetään kaavoja asteen pienentämiseen ja kirjoitetaan, että cos 2 x 2 = 1 + cos x 2 ja cos 2 2 x = 1 + cos 4 x 2. tarkoittaa,

y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) = sin (4 x) + 2 1 + cos 4 x 2 sin x cos (3 x) + 2 1 + cos x 2 - 1 sin (3 x) = = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x)

Nimittäjässä meillä on kaava summan sinille. Sitten voit kirjoittaa sen näin:

y = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x ) = = 1 + cos (4 x) sin (4 x)

Saimme 3 integraalin summan.

∫ sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) d x = = ∫ d x + cos (4 x) d x sin (4 x) + ∫ d x sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C

Joissakin tapauksissa integraalin alla olevat trigonometriset funktiot voidaan pelkistää murto-osiksi rationaalisiksi lausekkeiksi käyttämällä standardikorvausmenetelmää. Otetaan ensin kaavat, jotka ilmaisevat sin, cos ja t g puoliargumentin tangentin kautta:

sin x = 2 t g x 2 1 + t g 2 x 2 , sin x = 1 - t g 2 x 2 1 + t g 2 x 2 , t g x = 2 t g x 2 1 - t g 2 x 2

Meidän on myös ilmaistava differentiaali d x puolikulman tangentin avulla:

Koska d t g x 2 = t g x 2 "d x = d x 2 cos 2 x 2, niin

d x = 2 cos 2 x 2 d t g x 2 = 2 p t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 p t g x 2 1 + t g 2 x 2

Siten sin x = 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t g x 2 z 1 - z 2, d x = 2 d z 1 + z 2 kohdassa z = t g x 2.

Esimerkki 2

Etsi epämääräinen integraali ∫ d x 2 sin x + cos x + 2 .

Ratkaisu

Käytämme standarditrigonometrisen substituution menetelmää.

2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 d z z 2 + 4 z + 3

Saadaan, että ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .

Nyt voimme laajentaa integrandin yksinkertaisiksi murtoluvuiksi ja saada kahden integraalin summan:

∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C l n + z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C

∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C

Vastaus: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C

On tärkeää huomata, että ne kaavat, jotka ilmaisevat funktioita puoliargumentin tangentin kautta, eivät ole identiteettiä, joten tuloksena oleva lauseke ln t g x 2 + 1 t g x 2 + 3 + C on funktion y = 1 2 antiderivaatat. sin x + cos x + 2 vain määritelmäalueella.

Voit ratkaista muuntyyppisiä ongelmia käyttämällä perusintegrointimenetelmiä.

Jos huomaat tekstissä virheen, korosta se ja paina Ctrl+Enter

Trigonometristen funktioiden integraalit.
Esimerkkejä ratkaisuista

Päällä tämä oppitunti tarkastellaan trigonometristen funktioiden integraaleja, eli integraalien täyttö tulee olemaan sinejä, kosineja, tangentteja ja kotangentteja erilaisissa yhdistelmissä. Kaikki esimerkit analysoidaan yksityiskohtaisesti, helposti saatavilla ja ymmärrettäviä jopa teekannulle.

Trigonometristen funktioiden integraalien tutkiminen onnistuneesti edellyttää, että sinulla on hyvä käsitys yksinkertaisimmista integraaleista sekä hallittava joitain integrointitekniikoita. Näihin materiaaleihin voi tutustua luennoilla Epämääräinen integraali. Esimerkkejä ratkaisuista Ja .

Ja nyt tarvitsemme: Integraalien taulukko, Johdannaisten taulukko Ja Trigonometristen kaavojen hakemisto. Kaikki menetelmäkäsikirjoja löytyy sivulta Matemaattiset kaavat ja taulukot. Suosittelen tulostamaan kaiken. Keskityn erityisesti trigonometrisiin kaavoihin, niiden pitäisi olla silmiesi edessä– ilman tätä työn tehokkuus laskee huomattavasti.

Mutta ensin, mitä integraalit ovat tässä artikkelissa Ei. Muodolla ei ole integraaleja, - kosini, sini, kerrottuna jollain polynomilla (harvemmin jotain, jossa on tangentti tai kotangentti). Tällaiset integraalit integroidaan osittain, ja oppiaksesi menetelmän, vieraile oppitunnilla Integrointi osittain. Esimerkkejä ratkaisuista Myöskään tässä ei ole integraaleja "kaareilla" - arktangentti, arcsini jne., ne on myös useimmiten integroitu osilla.

Kun etsitään trigonometristen funktioiden integraaleja, käytetään useita menetelmiä:

(4) Käytämme taulukkokaavaa , ainoa ero on, että "X":n sijasta meillä on monimutkainen lauseke.

Esimerkki 2

Esimerkki 3

Etsi epämääräinen integraali.

Genren klassikko niille, jotka hukkuvat kilpailuun. Kuten luultavasti huomasit, integraalitaulukossa ei ole tangentin ja kotangentin integraalia, mutta tällaisia ​​integraaleja löytyy kuitenkin.

(1) Käytämme trigonometristä kaavaa

(2) Tuomme funktion differentiaalimerkin alle.

(3) Käytämme taulukkointegraalia .

Esimerkki 4

Etsi epämääräinen integraali.

Tämä on esimerkki itsenäisestä ratkaisusta, koko ratkaisu ja vastaus ovat oppitunnin lopussa.

Esimerkki 5

Etsi epämääräinen integraali.

Tutkintomme nousee vähitellen =).
Ensin ratkaisu:

(1) Käytämme kaavaa

(2) Käytämme trigonometristä päätunnusta , josta se seuraa .

(3) Jaa osoittaja termillä nimittäjän termillä.

(4) Käytämme epämääräisen integraalin lineaarisuusominaisuutta.

(5) Integroimme taulukon avulla.

Esimerkki 6

Etsi epämääräinen integraali.

Tämä on esimerkki itsenäisestä ratkaisusta, koko ratkaisu ja vastaus ovat oppitunnin lopussa.

On myös tangenttien ja kotangenttien integraaleja, joita on enemmän korkeat asteet. Tangentin kuution integraalia käsitellään oppitunnilla Kuinka laskea tasaisen hahmon pinta-ala? Neljännen ja viidennen potenssin tangentin (kotangentin) integraalit löytyvät sivulta Monimutkaiset integraalit.

Integrandin asteen vähentäminen

Tämä tekniikka toimii, kun integrandifunktiot on täytetty sinillä ja kosinilla jopa astetta. Voit pienentää astetta käyttämällä trigonometrisiä kaavoja , ja , ja viimeistä kaavaa käytetään usein päinvastaiseen suuntaan: .

Esimerkki 7

Etsi epämääräinen integraali.

Ratkaisu:

Periaatteessa tässä ei ole mitään uutta, paitsi että sovelsimme kaavaa (alentaa integrandin astetta). Huomaa, että olen lyhentänyt ratkaisua. Kokemuksen myötä integraali löytyy suullisesti, mikä säästää aikaa ja on täysin hyväksyttävää tehtävien viimeistelyssä. Tässä tapauksessa on suositeltavaa olla kuvailematta sääntöä , otamme ensin sanallisesti integraalin 1, sitten .

Esimerkki 8

Etsi epämääräinen integraali.

Tämä on esimerkki itsenäisestä ratkaisusta, koko ratkaisu ja vastaus ovat oppitunnin lopussa.

Tämä on luvattu tutkinnonkorotus:

Esimerkki 9

Etsi epämääräinen integraali.

Ensin ratkaisu, sitten kommentit:

(1) Valmistele integrandi soveltamaan kaavaa .

(2) Käytämme itse asiassa kaavaa.

(3) Nelitetään nimittäjä ja otetaan vakio pois integraalimerkistä. Sen olisi voinut tehdä hieman toisin, mutta mielestäni se oli kätevämpi.

(4) Käytämme kaavaa

(5) Kolmannella termillä pienennämme taas astetta, mutta käyttämällä kaavaa .

(6) Esittelemme samanlaisia ​​termejä (tässä jaoin termit termeiltä ja teki lisäyksen).

(7) Itse asiassa otamme integraalin, lineaarisuussäännön ja menetelmä funktion liittämiseksi erotusmerkin alle suoritetaan suullisesti.

(8) Vastauksen yhdistäminen.

! SISÄÄN epämääräinen integraali Usein vastaus voidaan kirjoittaa monella tavalla

Juuri tarkasteltavassa esimerkissä lopullinen vastaus olisi voitu kirjoittaa eri tavalla - avaamalla sulut ja jopa tekemällä tämän ennen lausekkeen integrointia, eli seuraava esimerkin lopetus on täysin hyväksyttävä:

On täysin mahdollista, että tämä vaihtoehto on vielä kätevämpi, selitin sen vain tavalla, jolla olen tottunut ratkaisemaan sen itse). Tässä on toinen tyypillinen esimerkki itsenäisestä ratkaisusta:

Esimerkki 10

Etsi epämääräinen integraali.

Tämä esimerkki voidaan ratkaista kahdella tavalla, ja saatat onnistua kaksi täysin erilaista vastausta(tarkemmin sanottuna ne näyttävät täysin erilaisilta, mutta matemaattisesta näkökulmasta ne ovat vastaavia). Todennäköisesti et näe järkevintä menetelmää ja kärsit sulujen avaamisesta ja muiden trigonometristen kaavojen käytöstä. Suurin osa tehokas ratkaisu annetaan oppitunnin lopussa.

Yhteenvetona kappaleesta päätämme: mikä tahansa lomakkeen integraali , missä ja - jopa numerot, ratkaistaan ​​menetelmällä, jolla vähennetään integrandin astetta.
Käytännössä törmäsin integraaleihin, joissa on 8 ja 10 astetta, ja minun piti ratkaista niiden kauhea sotku alentamalla astetta useita kertoja, mikä johti pitkiin, pitkiin vastauksiin.

Muuttujan korvausmenetelmä

Kuten artikkelissa mainittiin Muuttujan muutosmenetelmä määrittelemättömässä integraalissa, korvausmenetelmän käytön pääedellytys on se, että integrandissa on tietty funktio ja sen derivaatta:
(toiminnot eivät välttämättä ole tuotteessa)

Esimerkki 11

Etsi epämääräinen integraali.

Katsomme johdannaisten taulukkoa ja huomaamme kaavat, , eli integrandissamme on funktio ja sen derivaatta. Näemme kuitenkin, että differentioinnin aikana kosini ja sini muuttuvat toisiaan, ja herää kysymys: kuinka tehdä muuttujan muutos ja mitä tarkoitamme sinillä tai kosinilla?! Kysymys voidaan ratkaista tieteellisellä näkemisellä: jos suoritamme vaihdon väärin, siitä ei seuraa mitään hyvää.

Yleinen ohje: vastaavissa tapauksissa sinun on määritettävä nimittäjässä oleva funktio.

Keskeytämme ratkaisun ja teemme vaihdon

Nimittäjässä kaikki on kunnossa, kaikki riippuu vain , nyt on vielä selvitettävä, mitä siitä tulee.
Tätä varten löydämme eron:

Tai lyhyesti sanottuna:
Tuloksena olevasta yhtäläisyydestä ilmaisemme suhteesääntöä käyttäen tarvitsemamme lausekkeen:

Niin:

Nyt koko integrandimme riippuu vain ja voimme jatkaa ratkaisemista

Valmis. Muistutan, että korvaamisen tarkoituksena on yksinkertaistaa integradia; tässä tapauksessa kaikki meni integraatioon tehotoiminto taulukon mukaan.

Ei ole sattumaa, että kuvailin tätä esimerkkiä niin yksityiskohtaisesti; tämä tehtiin oppitunnin materiaalien toiston ja vahvistamisen vuoksi Muuttujan muutosmenetelmä määrittelemättömässä integraalissa.

Ja nyt kaksi esimerkkiä omasta ratkaisustasi:

Esimerkki 12

Etsi epämääräinen integraali.

Esimerkki 13

Etsi epämääräinen integraali.

Täydelliset ratkaisut ja vastaukset oppitunnin lopussa.

Esimerkki 14

Etsi epämääräinen integraali.

Tässä taas integrandissa on sini ja kosini (funktio, jolla on derivaatta), mutta tulossa syntyy dilemma - mitä tarkoitamme sinillä tai kosinilla?

Voit yrittää suorittaa korvauksen tieteellisellä menetelmällä, ja jos mikään ei toimi, määritä se toiseksi toiminnoksi, mutta siellä on:

Yleinen ohje: sinun on määritettävä toiminto, joka on kuvaannollisesti "epämukavassa asennossa".

Näemme, että tässä esimerkissä opiskelijakosini "kärsii" tutkinnosta ja sini istuu vapaasti, itsestään.

Tehdään siis korvaava:

Jos jollakin on edelleen vaikeuksia muuttujan korvaamisen ja differentiaalin löytämisen algoritmin kanssa, sinun tulee palata oppitunnille Muuttujan muutosmenetelmä määrittelemättömässä integraalissa.

Esimerkki 15

Etsi epämääräinen integraali.

Analysoidaan integrandia, mitä pitäisi merkitä?
Muistetaan ohjeemme:
1) Funktio on todennäköisimmin nimittäjässä;
2) Toiminto on "epämukavassa asennossa".

Muuten, nämä ohjeet eivät päde vain trigonometrisille funktioille.

Sini sopii molempiin kriteereihin (etenkin toiseen), joten korvaaminen ehdottaa itseään. Periaatteessa vaihto voidaan jo suorittaa, mutta ensin olisi mukava selvittää, mitä tehdä? Ensin "nipistetään" yksi kosini:

Varaamme oman "tulevaisuuden" erotuksen

Ja ilmaisemme sen sinin kautta käyttämällä main trigonometrinen identiteetti:

Tässä nyt korvaava:

Yleissääntö: Jos integrandissa yksi trigonometrisista funktioista (sini tai kosini) on sisällä outo aste, sinun on "purrattava" yksi funktio parittomasta asteesta ja määritettävä toinen funktio sen taakse. Puhumme vain integraaleista, joissa on kosinit ja sinit.

Tarkastetussa esimerkissä meillä oli kosini parittomalla potenssilla, joten poimimme potenssista yhden kosinin ja nimesimme sen siniksi.

Esimerkki 16

Etsi epämääräinen integraali.

Asteet ovat nousussa =).
Tämä on esimerkki, jonka voit ratkaista itse. Koko ratkaisu ja vastaus oppitunnin lopussa.

Universaali trigonometrinen substituutio

Universaali trigonometrinen substituutio on yleinen tapaus muuttujakorvausmenetelmässä. Voit yrittää käyttää sitä, kun "et tiedä mitä tehdä". Mutta itse asiassa sen soveltamiseen on joitain ohjeita. Tyypillisiä integraaleja, joissa universaalia trigonometristä substituutiota on käytettävä, ovat seuraavat integraalit: , , , jne.

Esimerkki 17

Etsi epämääräinen integraali.

Universaali trigonometrinen substituutio toteutetaan tässä tapauksessa seuraavalla tavalla. Korvataan: . En käytä kirjainta, mutta kirjainta, tämä ei ole mikään sääntö, vaan taas olen tottunut ratkaisemaan asioita tällä tavalla.

Tässä on helpompi löytää ero; tätä varten ilmaisen tasa-arvosta:
Liitän molempiin osiin arctangentin:

Arktangentti ja tangentti kumoavat toisensa:

Täten:

Käytännössä sinun ei tarvitse kuvata sitä niin yksityiskohtaisesti, vaan käytä vain lopputulosta:

! Lauseke on voimassa vain, jos sinien ja kosinien alla on yksinkertaisesti "X" integraalille (josta puhumme myöhemmin) kaikki on hieman erilaista!

Korvattaessa sinit ja kosinit muuttuvat seuraaviksi murtoiksi:
, , nämä yhtäläisyydet perustuvat hyvin tunnettuihin trigonometrisiin kaavoihin: ,

Lopullinen malli voisi siis näyttää tältä:

Suoritetaan universaali trigonometrinen korvaus: