Laurent-sarjan eristetyt pisteet ja niiden luokittelu. Yksittäinen piste

Taylor-sarjat toimivat tehokkaana työkaluna tutkia funktioita, jotka ovat analyyttisiä ympyrässä zol Rengasalueella analyyttisten funktioiden tutkimiseksi on mahdollista rakentaa laajennuksia muodon positiivisiin ja negatiivisiin potenssiin (z - zq). jotka yleistävät Taylorin laajennuksia. Sarjaa (1), joka ymmärretään kahden sarjan summana, kutsutaan Laurent-sarjaksi. On selvää, että sarjan (1) konvergenssialue on kunkin sarjan (2) konvergenssialueiden yhteinen osa. Etsitään hänet. Ensimmäisen sarjan konvergenssialue on ympyrä, jonka säde määräytyy Cauchyn-Hadamardin kaavan mukaan. Konvergenssiympyrän sisällä sarja (3) konvergoi analyyttiseksi funktioksi ja missä tahansa pienemmän säteen ympyrässä se suppenee ehdottomasti ja yhtenäisesti. Toinen rivi on teho sarja suhteessa muuttujaan sarja (5) konvergoituu konvergenssiympyränsä sisällä kompleksisen muuttujan m-*oo analyyttiseen funktioon ja missä tahansa pienemmän säteen ympyrässä se konvergoi absoluuttisesti ja tasaisesti, mikä tarkoittaa, että konvergenssialue sarjasta (4) on ympyrän ulkopuoli - Jos silloin on olemassa, sarjojen (3) ja (4) yhteinen konvergenssialue on ympyrärengas, jossa sarja (1) konvergoi analyyttiseksi funktioksi. Lisäksi missä tahansa renkaassa se suppenee ehdottomasti ja tasaisesti. Esimerkki 1. Määritä Rad Laurent -sarjan konvergenssialue Eristetyt yksittäispisteet ja niiden luokittelu M Ensimmäisen sarjan konvergenssialue on ympyrän ulkopuoli ja toisen sarjan konvergenssialue on ympyrän sisäpuoli. tämä sarja konvergoi ympyröiksi Lause 15. Mikä tahansa funktio f (z), yksiselitteinen ja apoliittinen ympyrärenkaassa, voidaan esittää tässä renkaassa konvergentin sarjan summana, jonka kertoimet Cn on määritetty yksiselitteisesti ja laskettu kaavojen mukaan missä 7p on ympyrä, jonka säde on m. Kiinnitetään mielivaltainen piste z renkaan R sisälle. Muodostetaan ympyröitä, joiden keskipisteet ovat pisteessä r, joiden säteet täyttävät epäyhtälöt ja tarkastelemme uutta rengasta Cauchyn integraalilausetta käyttämällä kerroinliitetylle alueelle, meillä on Muunnetaan erikseen jokainen summan (8) integraali. Kaikille ympyrän 7d* pisteille £ tasaisesti suppenevan sarjan 1 1 summasuhde täyttyy. Siksi murto-osa ^ voidaan esittää vi- / "/ kertomalla molemmat osat jatkuvalla funktiolla (O ja suorittamalla termi kerrallaan ympyrää pitkin, saadaan, että suoritamme toisen integraalin muunnoksen hieman eri tavalla. Kaikille ympyrän ir> pisteille £ suhde pätee. Siksi murto-osa ^ voidaan esittää summana Kertomalla molemmat puolet jatkuvalla funktiolla) ja integroimalla termisesti ympyrää 7/ pitkin saadaan, että Huomaa, että kaavojen (10) ja (12) integrandit ovat analyyttisiä funktioita ympyrärenkaassa. Siksi Cauchyn mukaan lause, vastaavien integraalien arvot eivät muutu, jos korvaamme ympyrät 7/r ja 7r/ millä tahansa ympyrällä. Näin voimme yhdistää kaavat (10) ja (12) , Korvaa integraalit oikealla puolella kaava (8) niiden lausekkeineen (9) ja (11), vastaavasti, saadaan vaadittu laajennus Koska z on mielivaltainen renkaan piste, tästä seuraa, että sarja (14) konvergoi funktioon f(z) kaikkialla tämä rengas, ja missä tahansa renkaassa sarja konvergoi ehdottomasti ja tasaisesti tähän funktioon. Osoittakaamme nyt, että muodon (6) hajoaminen on ainutlaatuinen. Oletetaan, että on vielä yksi laajennus, jolloin kaikkialla renkaan R sisällä on Ympyrällä sarjat (15) suppenevat tasaisesti. Kerrotaan yhtälön molemmat puolet (jossa m on kiinteä kokonaisluku ja integroidaan molemmat sarjat termi kerrallaan. Tuloksena saadaan vasemmalla puolella ja oikealla - Sch. Siten (4, = St. Koska m on mielivaltainen luku, viimeinen yhtälö todistaa laajennuksen yksilöllisyyden. Sarjaa (6), jonka kertoimet lasketaan kaavojen (7) avulla, kutsutaan renkaan f(z)-funktion Laurent-sarjaksi. tämän sarjan ehdot nro negatiivisia voimia nimeltään oikea osa Laurent-sarja, ja negatiivisten kanssa - sen pääosa. Laurent-sarjan kertoimien kaavoja (7) käytetään harvoin käytännössä, koska ne vaativat pääsääntöisesti hankalia laskelmia. Yleensä, jos mahdollista, käytetään valmiita perusfunktioiden Taylor-laajennuksia. Hajoamisen ainutlaatuisuuden perusteella mikä tahansa laillinen menetelmä johtaa samaan tulokseen. Esimerkki 2. Tarkastellaan Laurent-sarjan funktioiden laajennuksia eri alueilla, olettaen, että Fuiscia /(r):llä on kaksi yksikköpistettä: . Siten on kolme rengasmaista aluetta, joiden keskipiste on pisteessä r = 0. Jokaisessa niistä funktio f(r) on analyyttinen: a) ympyrä on rengas, ympyrän ulkopuoli (kuva 27). Etsitään funktion /(z) Laurent-laajennukset jokaiselta näistä alueista. Esitetään /(z) alkeismurtolukujen summana a) Ympyrä Muunnetaan relaatio (16) seuraavasti. Termien summan kaavalla geometrinen eteneminen, saadaan Korvaa löydetyt laajennukset kaavaan (17): Tämä laajennus on funktion /(z) Taylor-sarja. b) Funktion -r rengas pysyy suppenevana tässä renkaassa, koska sarja (19) funktiolle j^j |z| > 1 eroaa. Siksi muunnamme funktion /(z) seuraavasti: jälleen soveltamalla kaavaa (19) saadaan, että Tämä sarja konvergoi for. Korvaamalla laajennukset (18) ja (21) suhteeksi (20), saadaan c) Ympyrän ulkopuoli funktiolle -z |z|:lle. > 2 hajoaa, ja sarja (21) funktiolle- Esitetään funktio /(z) seuraavassa muodossa: /<*>Käyttämällä kaavoja (18) ja (19) saadaan TAI 1 Tämä esimerkki osoittaa, että samalle funktiolle f(z) Laurent-laajennuksella on yleisesti ottaen erilainen erilaisille renkaille. Esimerkki 3. Etsi funktion 8. Laurent-sarjan laajennus Laurent-sarja Eristetyt singulaaripisteet ja niiden luokittelu rengasalueella A Käytämme funktion f(z) esitystä seuraavassa muodossa: ja muunna toinen termi käyttämällä kaava geometrisen progression termien summalle, saadaan Korvaamalla löydetyt lausekkeet kaavaan (22), meillä on esimerkki 4. Laajenna funktio Laurent-sarjassa alueella zq = 0. Jokaiselle kompleksille on Let This laajennus pätee mille tahansa pisteelle z Ф 0. Tässä tapauksessa rengasalue edustaa koko kompleksista tasoa yhdellä hylätyllä pisteellä z - 0. Tämä alue voidaan määritellä seuraavalla suhteella: Tämä funktio on analyyttinen alueella From kaavoja ( 13) Laurent-sarjan kertoimille voidaan saada Kouiw-epäyhtälöt käyttämällä samaa päättelyä kuin edellisessä kappaleessa. jos funktio f(z) on rajattu ympyrään, jossa M on vakio), niin eristetyt pisteet Pistettä zo kutsutaan funktion f(z) eristetyksi singulaaripisteeksi, jos pisteen ( tätä joukkoa kutsutaan joskus pisteen 2o punkturoiduksi ympäristöksi, jossa funktio f(z) on ainutlaatuinen ja analyyttinen. Itse pisteessä zo funktio on joko määrittelemätön tai ei yksiselitteinen ja analyyttinen. Riippuen funktion /(r) käyttäytymisestä lähestyttäessä pistettä zo, erotellaan kolmenlaisia ​​yksittäispisteitä. Eristetyn singulaaripisteen sanotaan olevan: 1) irrotettava, jos on äärellinen 2) pmusach, jos 3) oleellisesti singulaaripiste, jos funktiolla f(z) ei ole rajaa kohdassa Eristetyn singulaaripisteen tyyppi liittyy läheisesti funktion Laurent-laajennuksen luonne pisteen keskellä. Laurent 16. Funktion f(z) eristetty singulaaripiste z0 on irrotettava piste, jos ja vain, jos funktion f(z) Laurentin laajennus pisteen zo lähistöllä ei sisällä pääosaa, ts. on muotoa Olkoon zo irrotettava yksikköpiste. Silloin on äärellinen, joten funktio f(z) on rajoitettu pisteen z prokologiseen ympäristöön. Laitamme Cauchyn epäyhtälöiden perusteella Koska p voidaan valita mielivaltaisen pieneksi, niin kaikki kertoimet negatiivisilla potenssilla (z) - 20) ovat yhtä suuria kuin nolla: päinvastoin, olkoon Laurentin funktion /(r) laajennus pisteen zq ympäristössä sisältää vain oikean osan, eli sillä on muoto (23) ja siksi on Taylor. On helppo nähdä, että z -* z0 funktiolla /(z) on raja-arvo: Lause 17. Funktion f(z) eristetty singulaaripiste zq on poistettavissa silloin ja vain, jos funktio J(z) on rajoittuu johonkin pisteen zq puhkaistuun alueeseen, Zgmechai ei. Olkoon r funktion /(r) irrotettava singulaaripiste. Olettaen, että funktio /(r) on analyyttinen jossain ympyrässä, jonka keskipiste on pisteessä r. Tämä määrittää pisteen nimen - irrotettava. Laurenti 18. Funktion f(z) eristetty singulaaripiste zq on napa silloin ja vain, jos funktion f(z) Laurentin laajennuksen pääosa pisteen läheisyydessä sisältää äärellisen (ja positiivisen) luvun nollasta poikkeavia termejä, eli sen muoto on 4 Olkoon z0 napa. Siitä lähtien pisteellä z0 on punkturoitu ympäristö, jossa funktio f(z) on analyyttinen ja ei-nolla. Sitten tässä naapurustossa määritellään analyyttinen funktio ja siksi piste zq on funktion irrotettava yksikköpiste (nolla) tai missä h(z) on analyyttinen funktio, h(z0) Φ 0. Sitten h(zo) Φ 0 on myös analyyttinen, silloin funktio φ on analyyttinen pisteen zq läheisyydessä, ja siksi mistä saamme sen. Oletetaan nyt, että funktiolla f(z) on muodon (24) laajennus pisteen pisteytetyssä ympäristössä. kohta zо. Tämä tarkoittaa, että tässä naapurustossa funktio f(z) on analyyttinen yhdessä funktion kanssa. Funktiolle g(z) pätee laajennus, josta voidaan nähdä, että zq on funktion g(z) irrotettava singulaaripiste ja on olemassa. Silloin funktio 0:ssa pyrkii olemaan funktion napa. on toinen yksinkertainen tosiasia. Piste Zq on funktion f(z) napa, jos ja vain jos funktio g(z) = yj voidaan laajentaa analyyttiseksi funktioksi pisteen zq läheisyydessä asettamalla g(z0) = 0. Järjestys funktion f(z) napaa kutsutaan funktion jfa nollakertaiseksi. Seuraava lause seuraa lauseista 16 ja 18. Laurent 19. Eristetty singulaaripiste on oleellisesti singulaarinen, jos ja vain jos Laurentin laajennuksen pääosa tämän pisteen puhkaisualueella sisältää äärettömän monta nollasta poikkeavaa termiä. Esimerkki 5. Funktion singulaaripiste on zo = 0. Meillä on Laurent-sarja Eristetyt singulaaripisteet ja niiden luokittelu Siksi zo = O on irrotettava singulaaripiste. Toiminnon /(z) laajennus Laurent-sarjaksi nollapisteen läheisyydessä sisältää vain oikean osan: Esimerkki7. /(z) = Funktion f(z) singulaaripiste on zq = 0. Tarkastellaan tämän funktion käyttäytymistä reaali- ja imaginaariakselilla: reaaliakselilla kohdassa x 0, imaginaariakselilla Näin ollen ei ole äärellinen eikä ääretön raja f(z):lle kohdassa z -* 0 ei ole olemassa. Tämä tarkoittaa, että piste r = 0 on funktion f(z) oleellisesti singulaaripiste. Etsitään funktion f(z) Laurentin laajennus nollapisteen läheisyydestä. Kaikille monimutkaisille C:lle olemme asettaneet. Sitten Laurentin laajennus sisältää äärettömän määrän termejä, joiden potenssit ovat negatiiviset z.

Kahden autonomisen differentiaaliyhtälön järjestelmillä kuvatut mallit.

Vaiheen taso. Vaihe muotokuva. Isoclin menetelmä. Pääisokliinit. Kestävyys vakaa tila. Lineaariset järjestelmät. Yksittäisten pisteiden tyypit: solmu, satula, tarkennus, keskus. Esimerkki: kemialliset reaktiot ensimmäinen tilaus.

Mielenkiintoisimmat tulokset biologisten järjestelmien ominaisuuksien kvalitatiivisesta mallintamisesta saatiin käyttämällä kahden differentiaaliyhtälön malleja, jotka mahdollistavat laadullinen tutkimus menetelmää käyttämällä vaihetaso. Tarkastellaan kahden autonomisen tavallisen differentiaaliyhtälön järjestelmää yleisnäkymä

(4.1)

P(x,y), Q(x,y)- jatkuvat toiminnot, määritelty jollain alueella G Euklidinen taso ( x,y ‑ Suorakulmaiset koordinaatit) ja joilla on tällä alueella jatkuvia derivaattoja, joiden kertaluokka on vähintään ensimmäinen.

Alue G voi olla joko rajoittamaton tai rajoitettu. Jos muuttujat x, y niillä on erityinen biologinen merkitys (ainepitoisuudet, lajien lukumäärä) useimmiten alueella G edustaa oikean puolitason positiivista kvadranttia:

0 £ x< ¥ ,0 £ y< ¥ .

Ainepitoisuuksia tai lajien lukumäärää voidaan rajoittaa myös ylhäältä aluksen tilavuudella tai elinympäristön pinta-alalla. Sitten muuttujien valikoimalla on muoto:

0 £ x< x 0 , 0 £ y< y 0 .

Muuttujat x, y muuttaa ajassa yhtälöjärjestelmän (4.1) mukaisesti niin, että jokainen järjestelmän tila vastaa muuttujaarvoparia ( x, y).

Toisaalta jokainen muuttujapari ( x, y) vastaa järjestelmän tiettyä tilaa.

Tarkastellaan tasoa koordinaattiakselilla, jolle muuttujien arvot piirretään x,y. Jokainen piste M tämä taso vastaa tiettyä järjestelmän tilaa. Tätä tasoa kutsutaan vaihetasoksi ja se edustaa järjestelmän kaikkien tilojen kokonaisuutta. Pistettä M(x,y) kutsutaan edustavaksi tai edustavaksi pisteeksi.

Anna heti alkuhetkellä t = t 0 edustavan pisteen koordinaatit M 0 (x(t 0), y(t 0)). Jokaisena seuraavana hetkenä t edustava piste siirtyy muuttujien arvojen muutosten mukaan x(t), y(t). Pisteiden kerääminen M(x(t), y(t)) vaihetasolla, jonka sijainti vastaa järjestelmän tiloja muuttujan muuttuessa ajan myötä x(t), y(t) yhtälöiden (4.1) mukaan kutsutaan vaiheen liikerata.

Vaihekulkureittien joukko muuttujien eri alkuarvoille antaa helposti näkyvän "muotokuvan" järjestelmästä. Rakentaminen vaiheen muotokuva voit tehdä johtopäätöksiä muuttujien muutosten luonteesta x, y tietämättä alkuperäisen yhtälöjärjestelmän analyyttisiä ratkaisuja(4.1).

Vaihemuotokuvan kuvaamiseksi on tarpeen rakentaa vektorikenttä järjestelmän liikeradan suunnista vaihetason jokaiseen pisteeseen. Lisäyksen asettaminenD t>0,saamme vastaavat lisäykset D x Ja D y ilmauksista:

D x=P(x,y)D t,

D y=Q(x,y)D t.

Vektorin suunta dy/dx kohdassa ( x, y) riippuu funktioiden etumerkistä P(x, y), Q(x, y) ja voidaan antaa taulukosta:

.(4.2)

Ratkaisu tähän yhtälöön y = y(x, c), tai implisiittisesti F(x,y)=c, Missä Kanssa– integrointivakio, antaa yhtälön (4.2) integraalikäyrien perheen - vaiheradat järjestelmä (4.1) koneessa x, y.

Isokliininen menetelmä

He käyttävät vaihekuvan rakentamiseen isokliinimenetelmä - vaihetasolle piirretään viivat, jotka leikkaavat integraalikäyrät tietyssä kulmassa. Isookliiniyhtälö voidaan helposti saada kohdasta (4.2). Laitetaan

Missä A– tietty vakioarvo. Merkitys A edustaa vaiheradan tangentin kaltevuuskulman tangenttia ja voi ottaa arvoja seuraavista:¥ kohtaan + ¥ . Korvaaminen sen sijaan dy/dx kohdassa (4.2) määrä A saamme isokliiniyhtälön:

.(4.3)

Yhtälö (4.3) määrittää jokaisessa tason pisteessä yksilöllisen tangentin vastaavalle integraalikäyrälle, lukuun ottamatta pistettä, jossa P(x,y)= 0, Q (x,y) = 0 , jossa tangentin suunta tulee epävarmaksi, koska derivaatan arvosta tulee epävarma:

.

Tämä piste on kaikkien isokliinien leikkauspiste - erityinen kohta. Siinä muuttujien aikaderivaatat katoavat samanaikaisesti x Ja y.

Siten yksittäisessä pisteessä muuttujien muutosnopeudet ovat nolla. Näin ollen vaiheratojen (4.2) differentiaaliyhtälöiden singulaaripiste vastaa järjestelmän paikallaan oleva tila(4.1), ja sen koordinaatit ovat muuttujien stationäärisiä arvoja x, y.

Erityisen kiinnostavia ovat pääisokliinit:

dy/dx=0, P(x,y)=0 – vaakasuuntaisten tangenttien isokliini ja

dy/dx=¥ ,Q(x,y)=0 – pystytangenttien isokliini.

Rakentamalla pääisokliinit ja etsimällä niiden leikkauspiste (x,y), jonka koordinaatit täyttävät ehdot:

löydämme siten vaihetason kaikkien isokliinien leikkauspisteen, jossa vaiheratojen tangenttien suunta on epävarma. Tämä - yksittäinen piste, joka vastaa järjestelmän paikallaan oleva tila(Kuva 4.2).

Järjestelmässä (4.1) on niin monta stationääristä tilaa kuin on pääisokliinien leikkauspisteitä vaihetasolla.

Jokainen vaiherata vastaa dynaamisen järjestelmän liikkeitä, jotka kulkevat samojen tilojen läpi ja eroavat toisistaan ​​vain aikalaskennan alussa.

Jos Cauchyn lauseen ehdot täyttyvät, niin jokaisen avaruuden pisteen kautta x, y, t on vain yksi integraalikäyrä. Sama pätee autonomian vuoksi vaiheratojen kohdalla: yksivaiheinen liikerata kulkee vaihetason jokaisen pisteen läpi.

Vakaustilan vakaus

Olkoon systeemi tasapainotilassa.

Tällöin edustava piste sijaitsee yhdessä järjestelmän singulaaripisteistä, jossa määritelmän mukaan:

.

Se, onko singulaaripiste stabiili vai ei, määräytyy sen mukaan, lähteekö edustava piste pienellä poikkeamalla paikallaan olevasta tilasta vai ei. Kahden yhtälön järjestelmän suhteen kielen stabiilisuuden määritelmäe, dseuraavasti.

Tasapainotila on stabiili, jos millä tahansa tietyllä tasapainotilasta poikkeavalla alueella (e )voit määrittää alueen d (e ), joka ympäröi tasapainotilaa ja jolla on ominaisuus, ettei alueen sisällä alkavaa liikerataa d , ei koskaan saavuta rajaa e . (Kuva 4.4)

Suurelle järjestelmäryhmälle - karkeita järjestelmiä – joiden käyttäytymisen luonne ei muutu pienellä yhtälöiden muodon muutoksella, tietoa käyttäytymisen tyypistä stationaarisen tilan läheisyydessä voidaan saada tutkimalla ei alkuperäistä, vaan yksinkertaistettua linearisoitu järjestelmä.

Lineaariset järjestelmät.

Harkitse kahden hengen järjestelmää lineaariset yhtälöt:

.(4.4)

Tässä a, b, c, d- vakiot, x, y- Suorakulmaiset koordinaatit vaihetasolla.

Etsimme yleistä ratkaisua muodossa:

.(4.5)

Korvataan nämä lausekkeet arvolla (4.4) ja vähennetään e l t:

(4.6)

Algebrallinen yhtälöjärjestelmä (4.6) tuntemattomien kanssa A, B sillä on nollasta poikkeava ratkaisu vain, jos sen determinantti, joka koostuu tuntemattomien kertoimista, on yhtä suuri kuin nolla:

.

Laajentamalla tätä determinanttia, saamme järjestelmän ominaisyhtälön:

.(4.7)

Tämän yhtälön ratkaiseminen antaa eksponenttiarvotl 1,2 , joille nollasta poikkeavat arvot ovat mahdollisia A Ja B yhtälön (4.6) ratkaisut. Nämä merkitykset ovat

.(4.8)

Jos radikaalilauseke on negatiivinen, niinl 1,2 kompleksikonjugaattiluvut. Oletetaan, että yhtälön (4.7) molemmilla juurilla on nollasta poikkeavat reaaliosat ja että useita juuria ei ole. Tällöin järjestelmän (4.4) yleinen ratkaisu voidaan esittää eksponentiaalien ja eksponentien lineaarisena yhdistelmänäl 1 , l 2 :

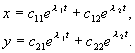(4.9)

Käytämme analysoidaksemme järjestelmän mahdollisten liikeratojen luonnetta vaihetasolla lineaarinen homogeeninen koordinaattimuunnos, joka johtaa järjestelmän kanoninen muoto:

,(4.10)

mahdollistaa kätevämmän esityksen vaihetasolla alkuperäiseen järjestelmään verrattuna (4.4). Otetaan käyttöön uudet koordinaatitξ , η kaavojen mukaan:

(4.1)

Lineaarialgebran kulusta tiedetään, että epäyhtälön tapauksessa reaaliosat nollataanl 1 , l 2 alkuperäinen järjestelmä (4.4) voidaan aina muuntaa muunnoksilla (4.11) kanoniseen muotoon (4.10) ja tutkia sen käyttäytymistä vaihetasollaξ , η . Tarkastellaanpa erilaisia ​​tapauksia, jotka voivat esiintyä tässä.

Juuret λ 1 , λ 2 – voimassa ja samalla merkillä

Tässä tapauksessa muunnoskertoimet ovat todellisia, siirrytään reaalitasostax,ytodelliseen tasoon ξ, η. Jakamalla toisen yhtälön (4.10) ensimmäisellä, saadaan:

.(4.12)

Integroimalla tämän yhtälön löydämme:

Missä .(4.13)

Sovitaan, että ymmärrämme λ:lla 2 ominaisyhtälön juuri, jolla on suuri moduuli, joka ei riko päättelymme yleisyyttä. Sitten, koska tarkasteltavassa tapauksessa juuret λ 1 , λ 2 – voimassa ja samalla merkillä,a>1 , ja käsittelemme parabolisia integraalikäyriä.

Kaikki integraalikäyrät (paitsi akseli η , joka vastaa ) kosketa akselin alkupisteessä ξ, joka on myös yhtälön (4.11) integraalikäyrä. Koordinaattien origo on erityinen piste.

Selvitetään nyt edustavan pisteen liikesuunta vaiheratoja pitkin. Jos λ 1, λ 2 ovat negatiivisia, niin, kuten yhtälöistä (4.10) voidaan nähdä, |ξ|, |η| pienenee ajan myötä. Edustuspiste lähestyy koordinaattien origoa, mutta ei kuitenkaan koskaan saavuta sitä. Muuten tämä olisi ristiriidassa Cauchyn lauseen kanssa, jonka mukaan vain yksi vaiherata kulkee vaihetason kunkin pisteen läpi.

Tällainen erityinen piste, jonka läpi integraalikäyrät kulkevat, aivan kuin paraabeliperhe kulkee origon läpi ja sitä kutsutaan solmuksi (kuva 1). 4.5)

Solmutyypin tasapainotila kohdassa λ 1, λ 2 < 0 on Ljapunov stabiili, koska edustava piste liikkuu kaikkia integraalikäyriä pitkin kohti koordinaattien origoa. Tämä vakaa solmu. Jos λ 1, λ 2 > 0 siis |ξ|, |η| kasvaa ajan myötä ja edustava piste siirtyy pois koordinaattien origosta. Tässä tapauksessa erityinen kohta– epävakaa solmu .

Vaihetasolla x, y integraalikäyrien käyttäytymisen yleinen kvalitatiivinen luonne säilyy, mutta integraalikäyrien tangentit eivät ole yhteensopivia koordinaattiakseleiden kanssa. Näiden tangenttien kaltevuuskulma määräytyy kertoimien suhteen α , β , γ , δ yhtälöissä (4.11).

Juuret λ 1 , λ 2 – ovat voimassa ja eri merkkejä.

Muunna kohteesta koordinaatit x,y koordinaatteihin ξ, η taas todellista. Kanonisten muuttujien yhtälöt ovat jälleen muodossa (4.10), mutta nyt λ:n merkit 1, λ 2 ovat erilaisia. Vaihekulkureittien yhtälöllä on muoto:

Missä , (4.14)

Integroimalla (4.14), löydämme

(4.15)

Tämä yhtälö määrittelee hyperbolisen tyyppisen käyräperheen, jossa molemmat koordinaattiakselit ovat– asymptootit (at a=1 meillä olisi tasasivuisten hyperbolien perhe). Koordinaattiakselit ovat myös tässä tapauksessa integraalikäyriä– nämä ovat ainoat integraalikäyrät, jotka kulkevat origon läpi. Jokainenjoista koostuu kolmesta vaiheesta: kaksi liikettä tasapainotilaan (tai tasapainotilasta) ja tasapainotilasta. Kaikki muut integraalikäyrät– ovat hyperboleja, jotka eivät kulje origon läpi (kuva 1). 4.6) Tämä erikoispiste on ns "satula ». Vuoristosatulan lähellä olevat tasoviivat käyttäytyvät samalla tavalla kuin vaiheradat satulan läheisyydessä.

Tarkastellaan edustavan pisteen liikkeen luonnetta vaiheratoja pitkin lähellä tasapainotilaa. Olkoon esim.λ 1 > 0, λ 2<0 . Sitten edustava piste sijoitetaan akselille ξ , siirtyy pois origosta ja sijoitetaan akselille η – lähestyy loputtomasti koordinaattien alkupistettä, saavuttamatta sitä rajallisessa ajassa. Missä tahansa edustava piste on alkuhetkellä (lukuun ottamatta singulaaripistettä ja asymptootin pisteitä η =0), se siirtyy lopulta pois tasapainotilasta, vaikka se aluksi liikkuisi yhtä integraalikäyristä kohti singulaaripistettä.

Se on selvää yksittäinen piste, kuten satula, on aina epävakaa . Vain erityisesti valituissa alkuolosuhteissa asymptootissaη =0 järjestelmä lähestyy tasapainotilaa. Tämä ei kuitenkaan ole ristiriidassa väitteen kanssa järjestelmän epävakaudesta. Jos laskemme, että kaikki järjestelmän alkutilat vaihetasolla ovat yhtä todennäköisiä, sitten sellaisen alkutilan todennäköisyys, joka vastaa liikettä suunnassa Vastaanottaja yksikköpiste on yhtä suuri kuin nolla. Siksi mikä tahansa todellinen liike poistaa järjestelmän tasapainotilasta.Palataan koordinaatteihinx,y,saamme saman laadullisen kuvan liikeradan liikkeen luonteesta koordinaattien origon ympärillä.

Solmun ja satulan tarkasteltujen tapausten välinen raja on tapaus Kun esimerkiksi yksi tunnusomaisista indikaattoreista λ 1 , katoaa, mikä tapahtuu, kun järjestelmän determinantti- ilmaisu ad-bc=0(katso kaava 4.8 ). Tässä tapauksessa yhtälöiden (4.4) oikeanpuoleisten kertoimet ovat verrannollisia toisiinsa:

ja järjestelmän tasapainotiloina ovat kaikki suoran pisteet:

Loput integraalikäyrät ovat ryhmä yhdensuuntaisia ​​suoria viivoja, joilla on kulmakerroin , jota pitkin edustavat pisteet joko lähestyvät tasapainotilaa tai siirtyvät siitä pois, riippuen ominaisyhtälön λ toisen juuren merkistä 2 = a+d.(Kuva 4. 7 ) Tässä tapauksessa tasapainotilan koordinaatit riippuvat muuttujien alkuarvosta.

Juuret λ 1 , λ 2 – monimutkainenkonjugaatti

Tässä tapauksessa ihan oikeastix Ja y me teemme niillä on monimutkaisia ​​konjugaatteja ξ , η (4.10) . Kuitenkin ottamalla käyttöön toinen välimuunnos on myös tässä tapauksessa mahdollista pelkistää harkinta todelliseksi lineaariseksi homogeeniseksi muunnokseksi. Laitetaan:

(4.16)

Missä a,b, Ja u, v – todelliset arvot. Voidaan osoittaa, että muunnos alkaenx,y Vastaanottaja u, v on oletuksiemme mukaan todellinen, lineaarinen, homogeeninen, jonka determinantti on eri kuin nolla. Yhtälöiden perusteella(4.10, 4.16) meillä on:

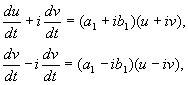
missä

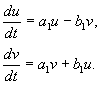(4.17)

Jakamalla toinen yhtälöstä ensimmäisellä, saamme:

joka on helpompi integroida, jos mennään napakoordinaatistoon (r, φ ) . Vaihdon jälkeen saamme mistä:

.(4.18)

Siis vaihetasollau, vkyseessä on logaritmisen spiraalien perhe, joista jokaisella onasymptoottinen piste alkuperässä.Yksittäinen piste, joka on asymptoottinen piste kaikista integraalikäyristä, jotka ovat spiraalin muotoisia, sisäkkäin jokaisessaystäväni, sitä kutsutaan keskittyä ( Kuva 4.8 ) .

Tarkastellaan edustavan pisteen liikkeen luonnetta vaiheratoja pitkin. Kerrotaan ensimmäinen yhtälöistä (4.17) luvullau, ja toinen päällä v ja lisäämällä saamme:

Missä

Antaa a 1 < 0 (a 1 = Reλ ) . Esittävä piste lähestyy sitten jatkuvasti koordinaattien origoa saavuttamatta sitä äärellisessä ajassa. Tämä tarkoittaa, että vaiheradat ovat kiertyviä spiraaleja ja vastaavat vaimennettuja värähtelyjä muuttujia. Tämä - vakaa keskittyminen .

Vakaan fokuksen tapauksessa, kuten stabiilin solmun tapauksessa, ei ainoastaan ​​Lyapunov-ehto täyty, vaan myös tiukempi vaatimus. Nimittäin mahdollisilla alkupoikkeamilla järjestelmä palaa ajan myötä niin lähelle tasapainoasemaa kuin halutaan. Sellaista vakautta, jossa alkupoikkeamat eivät vain kasva, vaan heikkenevät nollaan, kutsutaan absoluuttinen vakaus .

Jos kaavassa (4.18) a 1 >0 , silloin edustava piste siirtyy pois origosta, ja olemme tekemisissä epävakaa tarkennus . Kun siirrytään lentokoneestau, vvaihetasollex, yspiraalit pysyvät myös spiraaleina, mutta ne vääntyvät.

Tarkastellaanpa nyt tapausta, jolloina 1 =0 . Vaiheen liikeradat koneessau, vtulee olemaan ympyröitä joka lentokoneessax,yvastaavat ellipsiä:

Siis milloina 1=0 erityisen pisteen kauttax= 0, y= 0 integraalikäyrä ei kulje läpi. Tällaista eristettyä singulaaripistettä, jonka lähellä integraalikäyrät ovat suljettuja käyriä, erityisesti toisiinsa upotettuja ja singulaaripisteen sulkevia ellipsejä, kutsutaan keskipisteeksi.

Siten kuusi tyyppistä tasapainotilaa on mahdollista, riippuen ominaisyhtälön (4.7) juurien luonteesta. Näkymä vaiheradoista tasossa x, y näille kuudelle tapaukselle on esitetty kuvassa. 4.9.

Riisi. 4.9.Vaihemuotokuvien tyypit kiinteän tilan läheisyydessä lineaariyhtälöjärjestelmälle (4.4).

Viisi tasapainotilatyyppiä ovat karkeita, niiden luonne ei muutu riittävän pienillä muutoksilla yhtälöiden (4.4) oikealla puolella. Tässä tapauksessa muutosten ei vain oikealla puolella, vaan myös niiden ensimmäisen kertaluvun johdannaisissa tulisi olla pieniä. Kuudes tasapainotila – keskus – ei ole karkea. Pienillä muutoksilla yhtälöiden oikean puolen parametreissa siitä tulee vakaa tai epävakaa fokus.

Bifurkaatiokaavio

Otetaan käyttöön seuraava merkintä:

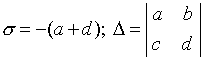. (4.11)

Sitten ominaisyhtälö kirjoitetaan seuraavasti:

. (4.12)

Tarkastellaan tasoa, jolla on suorakulmaiset suorakulmaiset koordinaatit s , D ja merkitse siihen alueet, jotka vastaavat yhtä tai toista tasapainotilatyyppiä, joka määräytyy ominaisyhtälön juurien luonteen mukaan

.(4.13)

Tasapainotilan stabiilisuuden ehtona on y:n negatiivisen reaaliosan läsnäolol 1 ja l 2 . Välttämätön ja riittävä ehto tälle on eriarvoisuuksien täyttyminens > 0, D > 0 . Kaaviossa (4.15) tämä ehto vastaa parametritason ensimmäisellä neljänneksellä olevia pisteitä. Yksittäinen piste on painopiste, josl 1 ja l 2 monimutkainen. Tämä ehto vastaa niitä tason pisteitä, joille , nuo. pisteet paraabelin kahden haaran välissäs 2 = 4 D. Akselipisteet s = 0, D>0, vastaavat keskustyypin tasapainotiloja. Samoinl 1 ja l 2 - ovat voimassa, mutta eri merkkisiä, ts. yksittäinen piste on satula jos D<0, jne. Tuloksena saamme kaavion parametritason osiosta s, D, alueiksi, jotka vastaavat erityyppisiä tasapainotiloja.

Riisi. 4.10. Bifurkaatiokaavio

lineaariselle yhtälöjärjestelmälle 4.4

Jos lineaarisen järjestelmän kertoimet a, b, c, d riippuu tietystä parametrista, sitten kun tämä parametri muuttuu, myös arvot muuttuvats , D . Rajat ylittäessä vaihekuvan luonne muuttuu laadullisesti. Siksi tällaisia ​​rajoja kutsutaan bifurkaatiorajoilla - rajan vastakkaisilla puolilla järjestelmässä on kaksi topologisesti erilaista vaihekuvaa ja vastaavasti kaksi erilaista käyttäytymistä.

Kaavio näyttää, kuinka tällaiset muutokset voivat tapahtua. Jos jätetään pois erikoistapaukset - koordinaattien origo - niin on helppo nähdä, että satula voi muuttua solmuksi, vakaaksi tai epävakaaksi, kun se ylittää ordinaatta-akselin. Vakaa solmu voi mennä joko satulaan tai vakaaseen fokukseen jne. Huomaa, että siirtymät stabiili solmu - vakaa fokus ja epävakaa solmu - epävakaa fokus eivät ole bifurkaatioita, koska vaiheavaruuden topologia ei muutu. Puhumme lisää vaiheavaruuden topologiasta ja bifurkaatiosiirtymistä luennossa 6.

Bifurkaatiosiirtymien aikana singulaaripisteen stabiilisuuden luonne muuttuu. Esimerkiksi vakaa tarkennus keskustan läpi voi muuttua epävakaaksi tarkennuksena. Tätä bifurkaatiota kutsutaan Andronov-Hopf haarautuminen sitä tutkineiden tiedemiesten nimien mukaan. Tämän bifurkaation aikana epälineaarisissa järjestelmissä syntyy rajasykli ja järjestelmä muuttuu itsevärähteleväksi (ks. luento 8).

Esimerkki. Lineaarinen kemiallinen reaktiojärjestelmä

Aine X virtaa ulkopuolelta vakionopeudella, muuttuu aineeksi Y ja aineen pitoisuuteen verrannollisella nopeudella Y, poistetaan reaktioalueelta. Kaikki reaktiot ovat ensiluokkaisia, paitsi ulkopuolelta tuleva aineen sisäänvirtaus, joka on nollakertaa. Reaktiokaavio näyttää tältä:

(4.14)

ja sitä kuvaa yhtälöjärjestelmä:

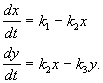(4.15)

Saamme kiinteät pitoisuudet rinnastamalla oikeanpuoleiset puolet nollaan:

.(4.16)

Tarkastellaan järjestelmän vaihekuvaa. Jaetaan järjestelmän (4.16) toinen yhtälö ensimmäisellä. Saamme:

.(4.17)

Yhtälö (4.17) määrittää muuttujien käyttäytymisen vaihetasolla. Tehdään tästä järjestelmästä vaihekuva. Piirretään ensin pääisokliinit vaihetasolle. Pystytangenttien isokliinin yhtälö:

Vaakasuuntaisten tangenttien isokliinin yhtälö:

Singulaarinen piste (stationaaritila) sijaitsee pääisokliinien leikkauskohdassa.

Määritetään nyt, missä kulmassa koordinaattiakselit leikkaavat integraalikäyrien kanssa.

Jos x= 0, siis.

Siten integraalikäyrien tangentin tangentti y=y(x), leikkaavat ordinaattisen akselin x=0, on negatiivinen ylemmässä puolitasossa (muista, että muuttujat x, y niillä on pitoisuusarvot, ja siksi olemme kiinnostuneita vain vaihetason oikeasta yläkvadrantista). Tässä tapauksessa tangentin kulman tangentti kasvaa etäisyyden myötä origosta.

Harkitse akselia y= 0. Kohdassa, jossa tämä akseli leikkaa integraalikäyrät, ne kuvataan yhtälöllä

klo abskissa-akselin ylittävien integraalikäyrien kaltevuuden tangentti on positiivinen ja kasvaa nollasta äärettömään kasvaessa x.

klo .

Tämän jälkeen kaltevuuskulman tangentti pienenee itseisarvossa, kun sitä kasvaa edelleen, pysyen negatiivisena ja pyrkii arvoon -1 x ® ¥ . Kun tiedät integraalikäyrien tangenttien suunnan pääisokliinilla ja koordinaattiakseleilla, on helppo muodostaa kokonaiskuva vaihereitoista.

Selvitetään singulaaripisteen stabiilisuuden luonne Lyapunov-menetelmällä. Järjestelmän ominaisdeterminantti on muotoa:

.

Laajentamalla determinanttia, saamme järjestelmän ominaisyhtälön: , eli Karakteriyhtälön juuret ovat molemmat negatiivisia. Näin ollen järjestelmän stationaaritila on vakaa solmu. Tässä tapauksessa aineen pitoisuus X pyrkii liikkumattomaan tilaan aina monotonisesti, aineen Y pitoisuus voi kulkea min tai max. Värähtelytilat ovat mahdottomia sellaisessa järjestelmässä.

Yksittäinen piste

matematiikassa.

1) Yhtälön F määrittämän käyrän singulaaripiste ( x, y) = 0, - piste M 0 ( x 0, y 0), jossa molemmat funktion F ( x, y) siirry nollaan:

Jos eivät kaikki funktion F ( x, y) pisteessä M 0 ovat yhtä suuret kuin nolla, niin O. t.:tä kutsutaan kaksinkertaiseksi. Jos ensimmäisten derivaattojen kanssa, jotka katoavat pisteessä M0, katoavat kaikki toiset, mutta eivät kaikki kolmannet derivaatat, yhtälöä kutsutaan kolmiosaiseksi jne. Kun tutkitaan käyrän rakennetta lähellä kaksois-O.t.:tä, lausekkeen etumerkillä on tärkeä rooli

Jos Δ > 0, niin avointa tilaa kutsutaan eristettyksi; esimerkiksi kaaressa v 2 - x 4 + 4x 2= 0 koordinaattien origo on eristetty O. t. (katso. riisi. 1 ). Jos Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - 4= 0 koordinaattien origo on solmu O. t. (katso. riisi. 2 ). Jos Δ = 0, käyrän yleinen piste on joko eristetty tai sille on tunnusomaista se, että käyrän eri haaroilla on tässä kohdassa yhteinen tangentti, esimerkiksi: a) 1. lajin kärkipiste - käyrän eri haarat käyrät sijaitsevat yhteisen tangentin vastakkaisilla puolilla ja muodostavat pisteen, kuten käyrän v 2 - x 3= 0 (katso riisi. 3 , a); b) 2. tyyppinen kärkipiste - käyrän eri haarat sijaitsevat yhteisen tangentin toisella puolella, kuten käyrä (y - x 2)2-x5= 0 (katso riisi. 3 , b); c) itsekosketuspiste (käyrää varten v 2 - x 4= 0 origo on itsekosketuspiste; (cm. riisi. 3 , V). Ilmoitetun O. t.:n ohella on monia muita erityisnimillä varustettuja O. t.:itä; Esimerkiksi asymptoottinen piste on spiraalin kärki, jossa on ääretön määrä kierroksia (ks. riisi. 4 ), päätepiste, kulmapiste jne.

2) Differentiaaliyhtälön singulaaripiste on piste, jossa differentiaaliyhtälön oikean puolen osoittaja ja nimittäjä katoavat samanaikaisesti (katso Differentiaaliyhtälöt)

jossa P ja Q ovat jatkuvasti differentioituvia funktioita. Olettaen, että O. t. sijaitsee koordinaattien origossa ja käyttämällä Taylorin kaavaa (katso Taylorin kaava), voimme esittää yhtälön (1) muodossa

missä P 1 ( x, y) ja Q 1 ( x, y) - äärettömän pieni suhteessa

Nimittäin jos λ 1 ≠ λ 2 ja λ 1 λ 2 > 0 tai λ 1 = λ 2, niin O.t. on solmu; kaikki integraalikäyrät, jotka kulkevat solmun riittävän pienen lähialueen pisteiden läpi, tulevat siihen. Jos λ 1 ≠ λ 2 ja λ 1 λ 2 i β, α ≠ 0 ja β ≠ ​​0, niin yleinen piste on fokus; kaikki integraalikäyrät, jotka kulkevat pisteiden läpi riittävän pienellä tarkennusalueella, edustavat spiraaleja, joissa on ääretön määrä kierroksia missä tahansa mielivaltaisen pienessä fokuksen ympäristössä. Jos lopulta λ 1,2 = ± iβ, β ≠ 0, silloin O. t:n luonnetta ei määritetä pelkästään lineaarisilla termeillä P ( x, y) ja Q ( x, y), kuten kaikissa edellä mainituissa tapauksissa; tässä O. t. voi olla painopiste tai keskus tai siinä voi olla enemmän monimutkainen luonne. Keskustan läheisyydessä kaikki integraalikäyrät ovat suljettuja ja sisältävät keskuksen sisällään. Joten esimerkiksi piste (0, 0) on yhtälöiden solmu klo" = 2u/x(λ 1 = 1, λ 2 = 2; katso riisi. 5 , a) ja y" = u/x(λ 1 = λ 2 = 1; katso riisi. 5 , b), yhtälön satula y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. riisi. 6 ), yhtälön painopiste y" =(x + y) / (x - y) (λ 1 = 1 - i, λ 2 = 1 + i; cm. riisi. 7 ) ja yhtälön keskipiste y" = -x/y(λ 1 = -i, λ 2 = i; cm. riisi. 8 ).

Jos x, y) ja Q ( x, y) analyyttinen, naapuruston O. t. ylempi määräys voidaan jakaa alueisiin: D 1 - täytetty integraalikäyrillä, molemmat päät sisältyvät O. t.:iin (elliptiset alueet), D 2 - täytetty integraalikäyrillä, toinen pää sisältyy O. t.:iin (paraboliset alueet), ja D 3 - alueet , joita rajoittaa kaksi yleiseen teoriaan sisältyvää integraalikäyrää, joiden välissä sijaitsevat hyperbolatyyppiset integraalikäyrät (hyperboliset alueet) (ks. riisi. 9 ). Jos yleispisteessä ei ole integraalikäyriä, yleistä pistettä kutsutaan stabiilityyppiseksi pisteeksi. Stabiilin oskillaattorin ympäristö koostuu suljetuista integraalikäyristä, jotka sisältävät osmoosin itsessään ja joiden välissä on spiraaleja (ks. riisi. 10 ).

Differentiaaliyhtälöiden tutkiminen, eli olennaisesti integraalikäyrien perheiden käyttäytymisen tutkimus differentiaaliyhtälöiden läheisyydessä, on yksi differentiaaliyhtälöiden kvalitatiivisen teorian haaroista ja sillä on tärkeä rooli sovelluksissa, erityisesti liikkeen vakauden kysymyksiä (A. M. Lyapunovin, A. Poincarén teokset jne.).

3) Yksiarvoisen analyyttisen funktion singulaaripiste on piste, jossa funktion analyyttisyys rikotaan (katso Analyyttiset funktiot). Jos naapurustossa on O. t. a, vapaa muista O. t., sitten kohta A kutsutaan eristetyksi O. t. Jos A- eristetty yleinen teoria ja on olemassa äärellinen a, kutsutaan irrotettavaksi yleisteoriaksi. Muuttamalla funktion määritelmää sopivasti pisteessä a (tai määrittelemällä se uudelleen tässä pisteessä, jos sen funktiota ei ole määritelty ollenkaan) nimittäin olettamalla f(a)= b, se on mahdollista saavuttaa a tulee korjatun funktion tavallinen piste. Esimerkiksi piste z= 0 on irrotettava O. t. funktiolle f 1 ( z) = f(z), Jos z≠ 0 ja f 1 (0), = 1, piste z= 0 on tavallinen piste [ f 1 (z) on pisteessä analyyttinen z= 0]. Jos A- eristettyä O. t.:tä ja a:ta kutsutaan napaksi tai funktion oleellisesti singulaaripisteeksi f(z), jos Laurent-sarja) toimii f(z) eristetyn O. t:n läheisyydessä ei sisällä negatiivisia tehoja z - a, Jos A- irrotettava O. t., sisältää äärellisen määrän negatiivisia asteita z - a, Jos A- napa (tässä tapauksessa navan järjestys R on määritelty korkein tutkinto a on olennaisesti yksittäinen piste. Esimerkiksi funktiolle

p = 2, 3, …)

piste z= 0 on järjestyksen napa R, toimintoa varten

piste z= 0 on olennaisesti singulaarinen piste.

Potenssisarjan konvergenssiympyrän rajalla on oltava vähintään yksi O.t. funktiosta, jota tiedot edustavat tässä ympyrässä teho sarja. Kaikki ainutlaatuisen analyyttisen funktion olemassaolon rajapisteet (luonnollinen raja) ovat tämän funktion rajoja. Siten kaikki yksikköympyrän pisteet | z| = 1 ovat erityisiä funktiolle

Moniarvoiselle analyyttiselle funktiolle "O. T." vaikeampaa. O. t.:n lisäksi funktion Riemannin pinnan yksittäisissä levyissä (eli yksiarvoisten analyyttisten elementtien O. t.:ssä) jokainen haarapiste on myös funktion O. t.. Riemannin pinnan eristetyt haarapisteet (eli sellaiset haarapisteet, joiden jossain naapurustossa ei ole missään lehdessä muita O. t. -funktioita) luokitellaan seuraavasti. Jos a on äärellinen haarapiste ja äärellinen a on olemassa, sitä kutsutaan kriittiseksi napaksi. Jos A- äärettömän kertaluvun eristettyä haarapistettä ja a kutsutaan transsendenttiseksi O.t.ksi. Kaikkia muita eristettyjä haarapisteitä kutsutaan kriittisiksi olennaisesti singulaaripisteiksi. Esimerkkejä: piste z= 0 on funktion f tavallinen kriittinen piste ( z) = loki z ja funktion kriittinen olennaisesti singulaaripiste f (z) = synti ln z.

Jokainen yleinen teoria, poistettavaa lukuun ottamatta, on este analyyttiselle jatkamiselle, eli analyyttinen jatkaminen käyrällä, joka kulkee pelkistymättömän yleisongelman läpi, on mahdotonta.

Iso Neuvostoliiton tietosanakirja. - M.: Neuvostoliiton tietosanakirja. 1969-1978 .

Katso, mitä "Singular point" tarkoittaa muissa sanakirjoissa:

Pisteet tästä. Katso myös yksikkökohta ( differentiaaliyhtälöt). Ominaisuus tai singulaarisuus matematiikassa on piste, jossa matemaattinen objekti (yleensä funktio) on määrittelemätön tai käyttäytyy epäsäännöllisesti (esimerkiksi piste, jossa ... ... Wikipedia

Analyyttinen toiminto on kohta, jossa analyyttisyysehtoja rikotaan. Jos analyyttinen funktio f(z) annetaan pisteen z0 tietyssä ympäristössä kaikkialla... Fyysinen tietosanakirja

Analyyttinen funktio on kohta, jossa funktion analyyttisyys rikotaan... Suuri Ensyklopedinen sanakirja

yksittäinen piste- - [Ja.N.Luginski, M.S.Fezi Žilinskaja, Yu.S.Kabirov. Englanti-venäläinen sähkötekniikan ja voimatekniikan sanakirja, Moskova, 1999] Sähkötekniikan aiheet, peruskäsitteet FI yksikkökohta ... Teknisen kääntäjän opas

1) Analyyttinen funktio f(z) on este kompleksisen muuttujan z funktion f(z) alkion analyyttiselle jatkamiselle mitä tahansa polkua pitkin tämän muuttujan tasolla. Määritelkää analyyttinen funktio f(z) jollain... ... Matemaattinen tietosanakirja

Analyyttinen funktio, piste, jossa funktion analyyttisyys rikotaan. * * * SINGLE POINT Analyyttisen funktion YKSI PISTE, piste, jossa funktion analyyttisyys rikotaan... tietosanakirja

yksittäinen piste- ypatingasis taškas statusas T ala automatika atitikmenys: engl. yksikköpiste vok. singularer Punkt, m rus. yksikköpiste, f pranc. pistehiukkas, m; point singulier, m … Automatikos terminų žodynas

yksittäinen piste- ypatingasis taškas statusas T ala fizika atitikmenys: engl. yksikköpiste vok. singularer Punkt, m rus. yksikköpiste, f pranc. point singulier, m … Fizikos terminų žodynas

Peruskäsitteet ja määritelmät:

Analyyttisen funktion f(z) nolla on piste "a", jolle f(a)=0.

Funktion f(z) kertaluvun "n" nolla on piste "a", jos fn(a)¹0.

Singulaaripistettä "a" kutsutaan funktion f(z) eristetyksi singulaariseksi pisteeksi, jos tämän pisteen ympäristössä ei ole muita singulaaripisteitä kuin "a".

Eristettyjä yksittäispisteitä on kolmenlaisia: .

1 irrotettava yksittäinen piste;

3 olennaisesti yksittäistä pistettä.

Singulaaripisteen tyyppi voidaan määrittää perustuen tietyn funktion käyttäytymiseen löydetyssä singulaaripisteessä sekä löydetyn singulaaripisteen läheisyydessä olevalle funktiolle saadun Laurent-sarjan muodosta.

Singulaaripisteen tyypin määrittäminen siinä olevan funktion käyttäytymisen perusteella.

1. Irrotettavat yksittäispisteet.

Funktion f(z) eristettyä singulaaripistettä a kutsutaan irrotettavaksi, jos sillä on äärellinen raja.

2.Puolat.

Funktion f(z) eristettyä singulaaripistettä a kutsutaan napaksi if .

3. Pohjimmiltaan yksikköpisteet.

Funktion f(z) eristettyä singulaaripistettä a kutsutaan oleellisesti singulaaripisteeksi, jos äärellistä tai ääretöntä ei ole olemassa.

Seuraava suhde on olemassa funktion nollien ja napojen välillä.

Jotta piste a olisi funktion f(Z) kertaluku n, on välttämätöntä ja riittävää, että tämä piste on funktion n kertaluvun nolla.

Jos n=1 napaa kutsutaan yksinkertaiseksi.

Määritelmä: Yksiselitteisen luonteen eristettyä yksittäistä pistettä kutsutaan:

a) irrotettava, jos hajoamisen pääosa puuttuu;

b) napa, jos pääosassa on äärellinen määrä termejä;

c) oleellisesti yksittäinen piste, jos pääosa sisältää äärettömän määrän termejä.

a) Siten irrotettavan singulaaripisteen läheisyydessä laajennus on muotoa:

se ilmaisee funktion ympyrän kaikissa pisteissä |z-a|

Keskuksessa z=a yhtäläisyys ei ole totta, koska funktiolla z=a on epäjatkuvuus, ja oikea puoli on jatkuva. Jos keskellä olevan funktion arvoa muutetaan siten, että se on yhtä suuri kuin oikean puolen arvo, niin aukko eliminoituu - tästä syystä nimi - irrotettava.

b) M kertaluvun navan läheisyydessä Laurent-sarjan laajennus on muotoa:

c) Yksinkertaisen pylvään läheisyydessä

Vähennykset ja niiden laskentakaavat.

Analyyttisen funktion f(z) jäännös eristetyssä singulaaripisteessä z 0 on kompleksiluku, joka on yhtä suuri kuin integraalin arvo , otettu positiiviseen suuntaan ympyrää L pitkin, jonka keskipiste on pisteessä z 0, joka on funktion f(z) analyyttisyysalueella (eli renkaassa 0<|z-z0|

Funktion f(z) jäännös eristetyssä singulaaripisteessä z 0 on merkitty symbolilla Res f(z 0) tai Res (f(z); z 0). Täten,

Res f(z 0)= . (22.15.1)

Jos laitamme n=-1 kaavaan (22.15.1), saamme:

C-1 =

tai Res f(z 0) = C-1,

nuo. funktion f(z) jäännös singulaaripisteen z 0 suhteen on yhtä suuri kuin Laurent-sarjan funktion f(z) laajennuksen ensimmäisen termin kerroin negatiivisella eksponentilla.

Vähennysten laskeminen.

Säännölliset tai irrotettavat yksittäispisteet. Ilmeisesti jos z=z 0 on funktion f(z) säännöllinen tai irrotettava singulaaripiste, niin Res f(z 0)=0 (Laurent-laajennuksesta näissä tapauksissa puuttuu pääosa, joten c-1=0) .

napa. Olkoon piste z 0 funktion f(z) yksinkertainen napa. Sitten Laurent-sarja funktiolle f(z) pisteen z 0 läheisyydessä on muotoa:

Täältä

Siksi, siirtämällä tämä yhtälö rajaan z --z 0, saamme

Res f(z0)=

Pohjimmiltaan erityinen kohta. Jos piste z 0 on funktion f(z) oleellisesti singulaaripiste, niin funktion jäännöksen laskemiseksi tässä pisteessä kerroin c-1 funktion Laurent-sarjan laajennuksessa määritetään yleensä suoraan.

Tapahtumien luokittelu. Summa, tapahtumien tulo, niiden ominaisuudet, graafinen esitys.

Tapahtumat on jaettu:

1. Satunnainen

2. Luotettava

3. Mahdotonta

Luotettava on tapahtuma, joka väistämättä tapahtuu tietyissä olosuhteissa (yö seuraa aamua).

Satunnainen tapahtuma on tapahtuma, joka voi tapahtua tai ei (kokeen läpäiseminen).

Mahdoton tapahtuma on tapahtuma, joka ei tapahdu tietyissä olosuhteissa (vihreän kynän saaminen ulos laatikosta, jossa on vain punaisia).

Antaa zq on funktion /(r) singulaaripiste, t.s. f(z) mutta on tässä vaiheessa analyyttinen (etenkään sitä ei ehkä määritellä siinä). Jos pisteen naapurustossa on tällainen reikä zq (eli joukko O z - zq f(z) on siis aialittinen zo nimeltään eristetty yksittäinen piste toimintoja f(z). Tämä määritelmä pysyy samana tapauksessa zn = oo, jos pisteen läheisyys lävistää jodin zq = oo ymmärtää joukko z> minä - ympyrän ulkopuoli, jonka keskipiste on origossa. Toisin sanoen erityinen kohta zq sanotaan olevan eristetty, jos tämän pisteen lähistöllä on ist muista yksittäisistä pisteistä kuin zq. Seuraavassa tarkastelemme vain yksittäisen merkin yksittäisiä pisteitä (funktio f(z) oletetaan olevan yksiselitteinen).

Riippuen funktion käyttäytymisestä f(z) klo z -> zq Yksittäisiä pisteitä on kolmenlaisia. Eristetty yksittäinen piste zq-funktiot f(z) nimeltään:

1) irrotettava yksittäinen piste, jos on rajallinen raja

2) napa, jos on raja

3) pohjimmiltaan erityinen kohta, Jos f(z) ei ole äärellistä eikä ääretöntä rajaa z-> zq.

Esimerkki 26.1. Osoittakaamme, että kaikki kolme singulaaripistetyyppiä toteutuvat. Harkitsemme f(z)= Piste zq = 0 on eristetty

tämän toiminnon erikoiskohta. Kaavan (22.12) avulla saadaan laajennus

josta seuraa, että on olemassa lim fi(z)= 1. Siksi zq = 0 on

on funktion irrotettava yksittäinen piste fi(z).

Toiminto f'j(z) =---on napa jossain pisteessä zo= 1 koska

2 r"X

Tarkastellaan nyt funktiota )з(z)= e 1 ^ r ja näytä se zo = O on tämän funktion olennaisesti yksittäinen piste. Kun yritetään z nollataan reaaliakselilla funktion /z vasen ja oikea raja (z) erilainen: lim Kanssa 1 / 1 = 0, lim s 1 /* = os. Tämä tarkoittaa,

x->0-0 x->0+O

Mitä f:i(z) ei ole äärellistä eikä ääretöntä rajaa 2:ssa -> Ai niin. zq = O on tämän funktion oleellisesti yksittäinen piste. (Huomaa, että kuten pointti näyttää z - iy nollaan imaginaarista akselifunktiota pitkin

ei ole rajaa ollenkaan.)

Tietenkin on olemassa eristämättömiä yksittäisiä pisteitä. Esimerkiksi. funktiolla on navat pisteissä z n = -, P= ±1, ±2,...

Siten, Zq = 0 on tämän funktion eristämätön yksittäispiste: missä tahansa (riippumatta siitä kuinka pienessä) tämän pisteen ympäristössä on muita singulaaripisteitä g s.

Antaa zo- funktion äärellinen eristetty singulaaripiste f(z). Sitten f(z) on samanlainen jossain 0 Zo-pisteen puhjennetussa naapurustossa zo tätä naapurustoa voidaan pitää renkaana, jonka sisäsäde r = 0. Lauseen 25.1 mukaan tarkasteltavana olevassa ympäristössä funktio f(z) voidaan laajentaa Laurent-sarjaksi (25.2). Osoitamme, että funktion käyttäytyminen kohdassa 2 -> zq (eli yksikköpisteen tyyppi zo) riippuu laajennuksen pääosan tyypistä (25.2); Tämä seikka selittää termin "pääosa" alkuperän.

Lause 2G.2. Funktion f(z) eristetty singulaaripiste zo on poistettavissa, jos ja vain jos Lorapov-laajennuksella tämän pisteen puhkaisualueella on oid

nuo. koostuu vain oikeasta osasta, ja kaikki pääosan kertoimet ovat yhtä suuria kuin luoti.

Todiste. 1. Anna zo- irrotettava yksittäinen piste. Osoittakaamme, että funktion Laurent-laajennus f(z) on muotoa (26.1). Erikoispisteestä lähtien zo irrotettava, silloin on rajallinen raja f(z) = A. Siten, f(z) on rajoittunut johonkin pisteen 0 z - zq lävistettyyn alueeseen zo, nuo. )(z) kaikille z tästä lähistöstä. Otetaan mikä tahansa R. U р /?| ja käytä kaavoja (25.3) Laurent-sarjan kertoimille:

Laajennuksen pääosan kertoimille n =- 1,-2,... Tällaisille arvoille P meillä on p~ s-e 0 klo R-> 0. Arvosta lähtien R voidaan valita mielivaltaisesti pieneksi herra~" voi olla niin pieni kuin halutaan. Koska |s ​​t,| ^ herra~p ja c„ eivät ole riippuvaisia ​​p:stä, niin c„ = 0 at Ja= - 1, -2,..., mikä oli todistettava.

2. Oletetaan nyt, että Laurent-laajennuksella on muoto (26.1). Sarja (26.1) on potenssisarja ja. siksi se konvergoi ei vain puhjennetulla alueella, vaan myös koko läheisyydessä z-zq piste mukaan lukien zo; sen määrä S(z) on analyyttinen z ja S(z) = )(z) 0z - zo R. Siksi on olemassa äärellinen raja )(z)= Pt 5(g) = 5(th) - Siksi singulaaripiste zq

Z->Zo Z-*Zo

irrotettava. Lause on todistettu.

Kommentti. Lauseen todistuksesta seuraa, että irrotettavan singulaaripisteen puhkaisualueella 0 z - zo funktio f(z) sopii yhteen funktion 5(r) kanssa, joka on analyyttinen koko naapurustossa z - zo. Siksi, jos asetamme /(th) = S(zq), sitten muuttamatta funktion arvoja f(z) missä tahansa pisteytetyn alueen pisteessä teemme tästä funktiosta analyyttisen Go:ssa, ts. "poistetaan" ominaisuus. Tämä selittää termin "irrotettava ominaisuus". On luonnollista, että tällaisia ​​pisteitä pidetään säännöllisinä, ei funktion yksittäisinä pisteinä f(z).

Harkitse esimerkiksi funktiota

Esimerkissä 26.1 osoitettiin, että Pm Nr) = 1. ts. yksittäinen piste

zq = 0 irrotettava. Asettamalla /i(0) = 1, eliminoimme siten singulaarisuuden ja saamme funktion, joka on analyyttinen kohdassa zq = 0 (ja koko C-tasolla).

Luonnehditaan nyt navat Laurentin laajennuksilla.

Lause 26.3. Funktion f(z) eristetty singulaaripiste Zo on napa silloin ja vain jos, kun Laurentin laajennuksen pääosassa, jonka keskusta on Zq, on vain äärellinen määrä erillisiä

nollakertoimista n:llä:

Todiste. 1. Anna zq - napa, ts. lim/( z) = oo.

Osoittakaamme, että funktion Laurent-laajennus f(z) on muotoa (2G.2). Koska lim f(z)= oo. silloin on pisteen puhjennut alue

ki zq. jossa f(z) on analyyttinen eikä siinä ole nollia. Sitten funktio g(z) = 1 /f(z) on myös analyyttinen tällä rei'itetyllä alueella, ja lim g(z)= 0. Siksi Zo on irrotettava *-? *0

funktion yksittäinen piste g(z). Määritellään g(z) pisteessä zo, laittaa g(zo)= 0. Sitten g(z) tulee analyyttiseksi koko (ei lävistetyn) pisteen alueella z 0 , ja z 0 on sen eristetty nolla. Merkitään N tämän nollan monikerta (kertaluku). Kuten §23 osoitti, pisteen läheisyydessä zq-funktio g(z) voidaan esittää muodossa (katso (23.2))

ja (z$) f 0 ja y>(z) on analyyttinen jossain pisteen läheisyydessä zo- Koska ip(z) jatkuva jossakin kohdassa zo Ja g>(zo) Ф 0" sitten ip(z) ei ole nollia jossain tämän pisteen läheisyydessä. Siksi toiminto 1 /-p(z) on myös analyyttinen tällä alueella ja siksi laajenee siinä Taylor-sarjassa:

Avaamalla sulut ja muuttamalla kertoimien nimiä, kirjoitamme viimeisen laajennuksen muotoon

missä c_jv = 1>o f 0. Näin ollen funktion /(r) Laurentin laajennuksen pääosa sisältää vain äärellisen määrän termejä; olemme päässeet haluttuun tasa-arvoon (26.2).

2. Päästä sisään puhjennut pisteiden ympäristö th toiminto )(z) edustaa Laurentin laajennus (26.2) (tarkempi muoto, katso (26.3)), jonka pääosa sisältää vain rajallisen määrän termejä, ja Kanssa- d" f 0. Se on todistettava Zq - funktionapa f(z). Kerrotaan yhtäläisyys (26.3) luvulla (G - G o) iV , saamme funktion

Sarja kohdassa (26.4) on potenssisarja, joka konvergoi analyyttiseksi funktioksi, ei vain lävistetyssä pisteessä, vaan myös koko pisteen ympäristössä Zq. Siksi toiminto h(z) tulee analyyttiseksi tällä naapurustolla, jos määrittelemme sen tarkemmin laittamalla h(zo)= s_dg f 0. Sitten

Siten piste th on napa ja Lause 26.3 on todistettu.

Nollafunktion monikertaisuus (järjestys). g(z)= 1//(g) kutsutaan napajärjestys funktio /(r). Jos N- th:n navan järjestys siis g(z)= (g - Zo) N ip(z), ja mene) F 0, ja kuten Lauseen 26.3 todistuksen ensimmäisessä osassa näkyy, funktion /(r) laajennus on muotoa (26.3), missä c_/v f 0. Kääntäen, jos /(r) laajennetaan sarjaan (26.3) ja e-i F 0 siis

t.s. N- funktion /(r) navan järjestys. Täten, zq-funktion napajärjestys/(G) yhtä suuri kuin Laurentin laajennuksen pääosan korkeimman nollasta poikkeavan kertoimen luku pisteen zq lävistetyssä ympäristössä(eli yhtä suuri kuin tämä luku N, mitä s_dg f 0 ja Sp= 0 at P > N).

Todistakaamme seuraava väite, joka on kätevä sovelluksille.

Seuraus 26.4. Piste zq on fiktion N kertaluvun napa/(G) silloin ja vain silloin/(G) edustava muodossa

missä h(z) on analyyttinen funktio pisteen läheisyydessä th ja h(zo)f 0.

Todiste. Toiminto cp(z) = l/h(z) on analyyttinen jossain pisteen h ympäristössä. Seurauksen 26.4 ehto vastaa seuraavaa:

Siksi zq - nolla monikertaisuus N toimintoja g(z). ja siksi moninaisuuden napa N funktiot /(2).

II Esimerkki 26.5. Etsi funktion yksittäiset pisteet ja määritä niiden tyyppi.

Ratkaisu: Pisteet, joissa (z 2 + 1 )(z+ Z) 2 = 0. Jos z 2 L- 1 = 0, sitten 2 = ±g Jos (z 4-3) 2 = 0 siis z= -3. Siksi funktiolla on kolme yksikköpistettä z= g, 22 = -g, Z3 = - 3. Harkitse z:

G - ensimmäisen asteen napa (käytimme Corollary 26.4). Se voidaan todistaa samalla tavalla, että 22 = -i myös ensimmäisen luokan pylväs. 2z:lle meillä on:

Siirrytään tarkastelemaan olennaisesti yksittäisiä kohtia.

Lause 26.6. Funktion f(z) eristetty singulaaripiste zq on oleellisesti singulaarinen silloin ja vain, jos Laurentin laajennuksen pääosassa, jonka keskusta on zq, on äärettömän monta erilaista. nolla, kertoimet p.

Todiste. Lause 26.6 seuraa suoraan lauseista 26.2 ja 26.3. Todellakin, jos kohta zq on olennaisesti erityinen, silloin Laurent-laajennuksen pääosa ei voi olla poissa tai sisältää äärellisen määrän termejä (muuten piste Zq on joko irrotettava tai sauva). Siksi pääosan termien lukumäärän on oltava ääretön.

Päinvastoin, jos pääosa sisältää äärettömän monta termiä, niin Zq ei voi olla irrotettava piste eikä napa. Tästä seuraa, että tämä kohta on pohjimmiltaan erityinen.

Määritelmän mukaan oleellisesti singulaaripisteelle on tunnusomaista se, että funktiolla /(2) ei ole äärellistä eikä ääretöntä rajaa. z ->zq. Täydellisempi käsitys siitä, kuinka epäsäännöllistä funktion käyttäytyminen oleellisesti singulaarisen pisteen läheisyydessä on, antaa seuraava lause.

Lause 26.7 (Sokhotskin lause). Jos zq on välttämätön henkilöille, funktion f(z), sitten mille tahansa kompleksiluvulle L, mukaan lukien A = vai niin, on pisteiden z n sarja siten, että z n -> zo ja lim f(zn) = A.

p->os

Todiste. Tarkastellaanpa ensin tapausta A = oo. Lauseen 2G.2 todistuksen ensimmäisessä osassa totesimme, että jos f(z) on rajoittunut johonkin pisteen r lävistettyyn ympäristöön, sitten kaikki kertoimet c", n = - Pääosan 1,- 2,... ovat yhtä kuin nolla (ja siksi singulaarisuus gossa on poistettavissa). Koska ehdon mukaan th on olennainen singulaaripiste, niin missä tahansa pisteen th pisteytetyssä ympäristössä funktio f(r) on rajoittamaton. Otetaanpa jokin vahva naapurusto 0 Z sellaisella tavalla f(zi) > 1 (jos |/(r)| z - zo I/2 on piste z-2 , jossa |/(yy)| > 2 jne.: puhjennetulla alueella O 71. On selvää, että r„ -e go ja lim /(r“) = oo. Eli tapauksessa A = oo, Lause 26.7

todistettu.

Anna sen nyt A f oo. Oletetaan ensin, että on puhjennut alue 0

= -yy---- on analyyttinen tällä rei'itetyllä alueella ja näin ollen

/(G) - A

Näin ollen go on funktion Φ(r) eristetty piste. Näytämme sinulle. että r on Φ(r:n) oleellisesti singulaaripiste. Tämä ei ehkä ole totta. Sitten on raja lim Ф(r), äärellinen tai ääretön. Hetkisen

/(r) = A +, silloin on myös Hsh /(r), joka on ristiriidassa ehdon kanssa

F(g) ~ :-*z 0

Näen lauseen. Siten r0 on funktion Φ(r) oleellisesti singulaaripiste. Edellä todistetun mukaan on olemassa pisteiden r n sarja, jossa r n th ja lim Ф(r n) = oo. Täältä

Olemme todistaneet vaaditun väitteen olettaen, että /(r) F A jossain pisteen lävistetyssä naapurustossa - Oletetaan nyt, että tämä on väärä, ts. missä tahansa mielivaltaisen pienessä pisteen th:n lävistetyssä ympäristössä on sellainen piste G", että /(r") = L. Sitten mille tahansa P pisteytetyssä naapurustossa 0 f(z u) = А. Siten haluttu lause on tosi P-juo

kaikissa tapauksissa, ja Lause 26.7 on todistettu.

Lauseen 26.7 (Sokhotsky) mukaan missä tahansa (mielisesti pienessä) oleellisesti singulaarisen pisteen puhkaisualueella funktio /(r) saa arvot mielivaltaisesti lähellä mitä tahansa laajennetusta kompleksitasosta C peräisin olevaa lukua.

Eristettyjen singulaaripisteiden tutkimiseen ovat usein hyödyllisiä jo tunnetut perusfunktioiden Taylor-laajennukset.

Esimerkki 2G.8. Määritä funktion singulaaripisteen tyyppi zq = 0

Ratkaistu ja e. Laajennetaan osoittaja ja nimittäjä Taylor-sarjaksi g:n potenssilla. Korvaaminen kohdassa (22.11) 3 z r:n sijaan ja vähentämällä 1, saamme

Käyttämällä (22.12) saamme nimittäjän laajennuksen:

Sarjat näissä laajennuksissa konvergoivat koko kompleksitasossa €. Meillä on

ja /2(2) ovat anariittisia pisteen läheisyydessä zo = 0 (ja jopa koko tasossa) ja /2(20) F 0 siis h(z) on myös analyyttinen jossain pisteen gF 0 ympäristössä. Seurauksen 26.4 mukaan piste Zo = 0 on järjestyksen napa N = 4.

II Esimerkki 26.9. Etsi funktion yksittäispisteet f(z)= sin j - ja määritä niiden tyyppi.

R e in e i e. Funktiolla on yksi äärellinen singulaaripiste zq = 1. Muissa pisteissä C:stä funktio w =--- analyyttinen; siksi funktio sin w tulee olemaan analyyttinen.

Korvaaminen - r:n sijasta sinin (22.12) laajennuksen saamme

Olemme saaneet funktion sin laajennuksen Laurent-sarjaksi pisteen 2o = 1 lävistetyssä ympäristössä. Koska tuloksena oleva laajennus sisältää äärettömän monta termiä, joilla on negatiivinen potenssi (r - 1), niin zq = 1 on oleellisesti yksittäinen piste (tässä tapauksessa Laurentin laajennus koostuu vain pääosasta ja säännöllinen osa puuttuu).

Huomaa, että singulaarisuuden luonne oli tässä tapauksessa mahdollista määrittää suoraan määritelmästä turvautumatta sarjalaajennukseen. Todellakin, on sekvenssejä (r",) ja (2"), jotka suppenevat zo= 1, ja niin f(z"n)= 1, /(2") = 0 (osoita tällaiset sekvenssit itse). f(z) ei ole rajaa z -> 1 ja siksi kohta zq - 1 on pohjimmiltaan erityinen.

Otetaan käyttöön funktion Laurentin laajennus pisteen ympäristössä Zq = 00 ja ota huomioon laajennuksen ja singulaarisuuden luonteen välinen yhteys tässä vaiheessa. Huomaa, että eristetyn yksittäisen pisteen ja sen tyypin (irrotettava, napainen tai olennaisesti yksittäinen) määritelmät siirtyvät tapaukseen zq = oc ilman muutoksia. Mutta lauseet 26.2. 26.3 ja 26.6, jotka liittyvät Laurentin laajennusten luonteeseen, on muutettava. Pointti on, että jäsenet cn(z- 2o) s. P= -1,-2,..., pääosa, joka määrittää funktion "epäsäännöllisyyden" lähellä loppupistettä Zq, koska 2 on yleensä oo, he käyttäytyvät "oikein" (yleensä 0). Päinvastoin, jäsenet oikean osan kanssa P= 1,2,... yleensä oo; ne määrittävät ominaisuuden luonteen Zq = oo. Siksi suurin osa oo:n lähialueen laajentumisesta muodostuu termeistä, joilla on positiivisia voimia P, ja oikea - negatiivisten kanssa.

Otetaan käyttöön uusi muuttuja w = 12. Toiminto tv = 1/2, laajennettu siten, että u(oo) = 0, yksi yhteen ja kartoittaa naapuruston yhdenmukaisesti z > R pisteitä zq = 00 |w|:n läheisyydessä wq = 0. Jos funktio f(z) analytiikka puhjennetulla alueella R z Zq = oc, sitten funktio G(w) = f(l/w) on analyyttinen suuressa naapurustossa 0 wo = 0. Koska klo 2 -> oo tulee olemaan w-> 0 siis

Siksi G(w) on pisteessä wq = 0 on samantyyppinen ominaisuus kuin f(z) pisteessä Zq = 00. Laajennetaan funktio G(w) Laurent-sarjaksi pisteen wo = 0 lävistetyssä ympäristössä:

(26.5):n oikealla puolella olevat summat edustavat laajennuksen säännöllistä ja pääosaa, vastaavasti. Siirrytään muuttujaan z, korvaamalla w = 1/z:

Nimeäminen P= -A*, 6* = 6_„ = s p ja sen huomaaminen G(l/z) = f(z), saamme

Hajoamista (2G.G) kutsutaan F(z)-funktion Laurent-laajennus pisteen zq lävistetyssä ympäristössä= oo. (2G.6):n ensimmäistä summaa kutsutaan oikea osa, ja toinen summa on pääosa tästä hajoamisesta. Koska nämä summat vastaavat oikeita ja pääasiallisia laajennuksen osia (26.5), niin lauseiden 26.2, 26.3 ja 26.6 analogit pätevät laajennukselle (26.6). Siten seuraava lause on Lauseen 26.2 analogi.

Lause 26.10. Eristetty yksittäinen pisteZq - OS (toiminnot/(G) on irrotettavissa, jos ja vain jos Laurent-laajennuksella tämän pisteen puhjennetussa naapurustossa on muoto

t.s. koostuu vain oikeasta osasta.

Laitetaan /(oo) = co. Funktio, jonka määrittää naapurustossa konvergoiva sarja (26.7). z > R piste 2o = oc, ns analyyttinen kohdassa z o = oo. (Huomaa, että tämä määritelmä vastaa funktion analyyttisuutta G(w) kohdassa voi = 0.)

Esimerkki 26.11. Tutki funktion singulaaripistettä zq = oo

Koska raja on siis rajallinen zo = oo on funktion /(r) irrotettava yksikköpiste. Jos laitamme /(oo) = lim J(z)= 0 siis f(z) tulee analyyttiseksi

tic pisteessä Zo= os. Osoitetaan kuinka vastaava laajennus (26.7) löydetään. Siirrytään muuttujaan w = 1 fz. Korvaaminen z= 1 /?е, saamme

(viimeinen yhtälö pätee pisteen wо = 0 punkturoidussa ympäristössä, mutta määritämme edelleen (7(0) = 0).) Tuloksena olevalla funktiolla on singulaaripisteitä w =± minä, w =-1/3, ja pisteessä Wq = 0 on analyyttinen. Avaustoiminto G(w) asteittain w(kuten tehtiin esimerkissä 25.7) ja korvaamalla tuloksena olevaan tehosarjaan w = 1/z, voimme saada funktion laajennuksen (26.7). f(z).

Lause 26.3 tapaukselle zo= oo kirjoitetaan uudelleen seuraavassa muodossa.

Lause 26.12. Eristetty yksittäinen piste th = os funktio f(z) on napa silloin ja vain jos se on Laurentin laajennuksen pääosa (26.6) sillä on vain äärellinen määrä nollasta poikkeavia kertoimia Kanssa":

Tässä sarja on säännöllinen osa ja suluissa oleva polynomi on laajennuksen pääosa. Napojen monikertaisuus oc:ssa määritellään napakertoimeksi wq = 0 funktiota G(z). On helppo nähdä, että navan monikertaisuus on sama kuin numero N vuonna (26.8).

Q p | (i 2 + 1) (z+3) 2

Tehtävä. Näytä, että toiminto f(z) =-- -- on mukana

kohta zo = oo järjestysnapa 3.

Lause 26.6 olennaisesti singulaarisesta pisteestä voidaan kirjoittaa uudelleen tapaukselle zo= os melkein sanatarkasti, emmekä käsittele tätä yksityiskohtaisesti.