Réduire les fractions impropres. Le calculateur en ligne pour réduire des fractions algébriques avec une solution détaillée vous permet de réduire une fraction et de convertir une fraction impropre en fraction propre

Si nous devons diviser 497 par 4, alors lors de la division, nous verrons que 497 n'est pas également divisible par 4, c'est-à-dire le reste de la division demeure. Dans de tels cas, on dit que c'est terminé division avec reste, et la solution s'écrit comme suit :
497 : 4 = 124 (1 reste).

Les composantes de division du côté gauche de l'égalité sont appelées de la même manière que dans la division sans reste : 497 - dividende, 4 - diviseur. Le résultat de la division divisée avec un reste est appelé privé incomplet. Dans notre cas, il s’agit du nombre 124. Et enfin, la dernière composante, qui n’est pas en division ordinaire, est reste. Dans les cas où il n’y a pas de reste, on dit qu’un nombre est divisé par un autre. sans laisser de trace, ou complètement. On pense qu'avec une telle division, le reste est nul. Dans notre cas, le reste est 1.

Le reste est toujours inférieur au diviseur.

La division peut être vérifiée par multiplication. Si, par exemple, il existe une égalité 64 : 32 = 2, alors la vérification peut se faire comme ceci : 64 = 32 * 2.

Souvent, dans les cas où une division avec un reste est effectuée, il est pratique d'utiliser l'égalité
une = b * n + r,
où a est le dividende, b est le diviseur, n est le quotient partiel, r est le reste.

Le quotient des nombres naturels peut s’écrire sous forme de fraction.

Le numérateur d'une fraction est le dividende et le dénominateur est le diviseur.

Puisque le numérateur d’une fraction est le dividende et le dénominateur est le diviseur, croire que la ligne d'une fraction signifie l'action de division. Parfois, il est pratique d’écrire la division sous forme de fraction sans utiliser le signe « : ».

Le quotient de la division des nombres naturels m et n peut s'écrire sous la forme d'une fraction \(\frac(m)(n)\), où le numérateur m est le dividende et le dénominateur n est le diviseur :
\(m:n = \frac(m)(n)\)

Les règles suivantes sont vraies :

Pour obtenir la fraction \(\frac(m)(n)\), vous devez diviser un par n parts égales(actions) et prendre ces parts.

Pour obtenir la fraction \(\frac(m)(n)\), vous devez diviser le nombre m par le nombre n.

Pour trouver une partie d'un tout, il faut diviser le nombre correspondant au tout par le dénominateur et multiplier le résultat par le numérateur de la fraction qui exprime cette partie.

Pour trouver un tout à partir de sa partie, il faut diviser le nombre correspondant à cette partie par le numérateur et multiplier le résultat par le dénominateur de la fraction qui exprime cette partie.

Si le numérateur et le dénominateur d'une fraction sont multipliés par le même nombre (sauf zéro), la valeur de la fraction ne changera pas :
\(\large \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)

Si le numérateur et le dénominateur d'une fraction sont divisés par le même nombre (sauf zéro), la valeur de la fraction ne changera pas :
\(\large \frac(a)(b) = \frac(a: m)(b: m) \)
Cette propriété est appelée propriété principale d'une fraction.

Les deux dernières transformations sont appelées réduire une fraction.

Si les fractions doivent être représentées comme des fractions avec le même dénominateur, alors cette action est appelée amener les fractions à un dénominateur commun.

Fractions propres et impropres. Numéros mixtes

Vous savez déjà qu'une fraction peut être obtenue en divisant un tout en parties égales et en prenant plusieurs de ces parties. Par exemple, la fraction \(\frac(3)(4)\) signifie trois quarts de un. Dans de nombreux problèmes du paragraphe précédent, les fractions étaient utilisées pour représenter des parties d’un tout. Bon sens suggère que la partie doit toujours être inférieure au tout, mais qu'en est-il des fractions telles que, par exemple, \(\frac(5)(5)\) ou \(\frac(8)(5)\) ? Il est clair que cela ne fait plus partie de l'unité. C'est probablement pourquoi les fractions dont le numérateur est supérieur ou égal au dénominateur sont appelées fractions impropres. Les fractions restantes, c'est-à-dire les fractions dont le numérateur est inférieur au dénominateur, sont appelées fractions correctes.

Comme vous le savez, toute fraction commune, propre ou impropre, peut être considérée comme le résultat de la division du numérateur par le dénominateur. Ainsi, en mathématiques, contrairement au langage ordinaire, le terme « fraction impropre » ne signifie pas que nous avons fait quelque chose de mal, mais seulement que le numérateur de cette fraction est supérieur ou égal au dénominateur.

Si un nombre est constitué d'une partie entière et d'une fraction, alors tel les fractions sont appelées mixtes.

Par exemple:
\(5:3 = 1\frac(2)(3)\) : 1 - partie entière, et \(\frac(2)(3)\) est la partie fractionnaire.

Si le numérateur de la fraction \(\frac(a)(b)\) est divisible par entier naturel n, puis pour diviser cette fraction par n, il faut diviser son numérateur par ce nombre :
\(\large \frac(a)(b) : n = \frac(a:n)(b) \)

Si le numérateur de la fraction \(\frac(a)(b)\) n'est pas divisible par un entier naturel n, alors pour diviser cette fraction par n, il faut multiplier son dénominateur par ce nombre :
\(\large \frac(a)(b) : n = \frac(a)(bn) \)

Notez que la deuxième règle est également vraie lorsque le numérateur est divisible par n. On peut donc l’utiliser lorsqu’il est difficile de déterminer au premier coup d’œil si le numérateur d’une fraction est divisible par n ou non.

Actions avec des fractions. Additionner des fractions.

Vous pouvez effectuer des opérations arithmétiques avec des nombres fractionnaires, tout comme avec des nombres naturels. Voyons d'abord ajouter des fractions. Il est facile d’additionner des fractions ayant les mêmes dénominateurs. Trouvons, par exemple, la somme de \(\frac(2)(7)\) et \(\frac(3)(7)\). Il est facile de comprendre que \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \)

Pour additionner des fractions avec les mêmes dénominateurs, vous devez additionner leurs numérateurs et laisser le dénominateur identique.

À l'aide de lettres, la règle d'addition de fractions ayant des dénominateurs similaires peut s'écrire comme suit :
\(\large \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)

Si vous devez ajouter des fractions avec différents dénominateurs, alors il faut d’abord les ramener à un dénominateur commun. Par exemple:
\(\large \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3 ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)

Pour les fractions, comme pour les nombres naturels, les propriétés commutatives et associatives de l'addition sont valables.

Ajouter des fractions mixtes

Les notations telles que \(2\frac(2)(3)\) sont appelées fractions mélangées. Dans ce cas, le chiffre 2 est appelé partie entière fraction mixte, et le nombre \(\frac(2)(3)\) est son partie fractionnaire. L’entrée \(2\frac(2)(3)\) se lit comme suit : « deux et deux tiers ».

En divisant le nombre 8 par le nombre 3, vous pouvez obtenir deux réponses : \(\frac(8)(3)\) et \(2\frac(2)(3)\). Ils expriment le même nombre fractionnaire, c'est-à-dire \(\frac(8)(3) = 2 \frac(2)(3)\)

Ainsi, la fraction impropre \(\frac(8)(3)\) est représentée comme une fraction mixte \(2\frac(2)(3)\). Dans de tels cas, on dit qu'à partir d'une fraction impropre a mis en évidence toute la partie.

Soustraire des fractions (nombres fractionnaires)

Soustraction nombres fractionnaires, comme les nombres naturels, est déterminé sur la base de l'action d'addition : en soustraire un autre à un nombre signifie trouver un nombre qui, ajouté au second, donne le premier. Par exemple:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) puisque \(\frac(7)(9)+\frac(1)(9 ) = \frac(8)(9)\)

La règle pour soustraire des fractions avec des dénominateurs similaires est similaire à la règle pour additionner de telles fractions :
Pour trouver la différence entre des fractions ayant les mêmes dénominateurs, vous devez soustraire le numérateur de la seconde du numérateur de la première fraction et laisser le dénominateur identique.

En utilisant des lettres, cette règle s'écrit ainsi :
\(\large \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)

Multiplier des fractions

Pour multiplier une fraction par une fraction, vous devez multiplier leurs numérateurs et dénominateurs et écrire le premier produit comme numérateur et le second comme dénominateur.

À l'aide de lettres, la règle de multiplication des fractions peut s'écrire comme suit :
\(\large \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)

À l'aide de la règle formulée, vous pouvez multiplier une fraction par un nombre naturel, par une fraction mixte, ainsi que multiplier des fractions mixtes. Pour ce faire, vous devez écrire un nombre naturel sous forme de fraction avec un dénominateur 1, une fraction mixte - sous forme de fraction impropre.

Le résultat de la multiplication doit être simplifié (si possible) en réduisant la fraction et en isolant toute la partie de la fraction impropre.

Pour les fractions, comme pour les nombres naturels, les propriétés commutatives et combinatoires de la multiplication, ainsi que la propriété distributive de la multiplication par rapport à l'addition, sont valables.

Division de fractions

Prenons la fraction \(\frac(2)(3)\) et « retournons-la », en échangeant le numérateur et le dénominateur. On obtient la fraction \(\frac(3)(2)\). Cette fraction est appelée inverse fractions \(\frac(2)(3)\).

Si nous « inversons » maintenant la fraction \(\frac(3)(2)\), nous obtiendrons la fraction originale \(\frac(2)(3)\). Par conséquent, des fractions telles que \(\frac(2)(3)\) et \(\frac(3)(2)\) sont appelées mutuellement inverse.

Par exemple, les fractions \(\frac(6)(5) \) et \(\frac(5)(6) \), \(\frac(7)(18) \) et \(\frac (18 )(7)\).

À l'aide de lettres, les fractions réciproques peuvent s'écrire comme suit : \(\frac(a)(b) \) et \(\frac(b)(a) \)

Il est clair que le produit des fractions réciproques est égal à 1. Par exemple : \(\frac(2)(3) \cdot \frac(3)(2) =1 \)

En utilisant des fractions réciproques, vous pouvez réduire la division de fractions à la multiplication.

La règle pour diviser une fraction par une fraction est :
Pour diviser une fraction par une autre, vous devez multiplier le dividende par l’inverse du diviseur.

À l'aide de lettres, la règle de division des fractions peut s'écrire comme suit :
\(\large \frac(a)(b) : \frac(c)(d) = \frac(a)(b) \cdot \frac(d)(c) \)

Si le dividende ou le diviseur est un nombre naturel ou une fraction mixte, alors pour utiliser la règle de division des fractions, il doit d'abord être représenté comme une fraction impropre.

En utilisant des fractions, la même partie d’un objet entier peut être écrite de différentes manières.

La moitié du cercle est ombrée sur l'image

Donc toutes ces fractions sont égales.

Pour plus de commodité, le facteur supplémentaire est inscrit sur la barre oblique à droite au-dessus de la fraction.

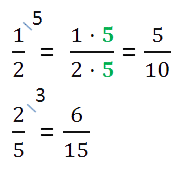
Revenons à nos fractions et écrivons-les dans un ordre différent.

Une fraction égale à un donné peut être obtenue si le numérateur et le dénominateur de la fraction sont simultanément divisés par le même nombre qui n'est pas égal à zéro.

Cette conversion d'une fraction s'appelle réduire une fraction.

La réduction d’une fraction s’écrit généralement comme suit.

Le numérateur et le dénominateur sont barrés et les résultats de la division (quotients) du numérateur et du dénominateur par le même nombre sont inscrits à côté d'eux.

Gardez à l’esprit le nombre par lequel le numérateur et le dénominateur sont divisés.

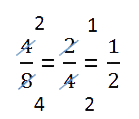
Dans notre exemple, nous avons réduit (c’est-à-dire divisé le numérateur et le dénominateur) une fraction par deux, ce que nous avons gardé à l’esprit.

La réduction des fractions peut être effectuée de manière séquentielle.

La propriété principale d'une fraction

Formulons la propriété principale d'une fraction.

Si le numérateur et le dénominateur d'une fraction sont multipliés ou divisés par le même nombre qui n'est pas égal à zéro, vous obtenez une fraction égale à celle donnée.

Écrivons cette propriété sous forme d'expressions littérales.

, où "a", "b" et "k" sont des nombres naturels.

Fractions réductrices, règles et exemples de fractions réductrices.

Dans cet article, nous verrons en détail comment fractions réductrices. Tout d’abord, parlons de ce qu’on appelle réduire une fraction. Après cela, parlons de la réduction d'une fraction réductible à une forme irréductible. Nous obtiendrons ensuite la règle de réduction des fractions et, enfin, considérerons des exemples d'application de cette règle.

Navigation dans les pages.

Que signifie réduire une fraction ?

Nous savons que les fractions ordinaires sont divisées en fractions réductibles et irréductibles. Vous pouvez deviner à partir des noms que les fractions réductibles peuvent être réduites, mais pas les fractions irréductibles.

Que signifie réduire une fraction ? Réduire la fraction- cela signifie diviser son numérateur et son dénominateur par leur positif et différent de l'unité diviseur commun. Il est clair qu'en raison de la réduction d'une fraction, une nouvelle fraction avec un numérateur et un dénominateur plus petits est obtenue et, en raison de la propriété fondamentale de la fraction, la fraction résultante est égale à l'originale.

Par exemple, réduisons la fraction commune 8/24 en divisant son numérateur et son dénominateur par 2. Autrement dit, réduisons la fraction 8/24 de 2. Puisque 8:2=4 et 24:2=12, cette réduction donne la fraction 4/12, qui est égale à la fraction originale 8/24 (voir fractions égales et inégales). En conséquence, nous avons .

Réduire des fractions ordinaires à une forme irréductible

En règle générale, le but ultime de la réduction d’une fraction est d’obtenir une fraction irréductible égale à la fraction réductible d’origine. Cet objectif peut être atteint en réduisant la fraction réductible originale par le plus grand diviseur commun de son numérateur et de son dénominateur. Grâce à une telle réduction, une fraction irréductible est toujours obtenue. En effet, une fraction est irréductible, puisque d'après les propriétés de GCD on sait que Et - mutuellement nombres premiers. Nous dirons ici que le plus grand diviseur commun du numérateur et du dénominateur d'une fraction est le plus grand nombre par lequel cette fraction peut être réduite.

Donc, réduire une fraction commune à une forme irréductible consiste à diviser le numérateur et le dénominateur de la fraction réductible originale par leur pgcd.

Regardons un exemple, pour lequel on revient à la fraction 8/24 et on la réduit du plus grand diviseur commun des nombres 8 et 24, qui est égal à 8. Puisque 8:8=1 et 24:8=3, on arrive à la fraction irréductible 1/3. Donc, .

Notez que l’expression « réduire une fraction » signifie souvent réduire la fraction originale à sa forme irréductible. En d’autres termes, réduire une fraction consiste très souvent à diviser le numérateur et le dénominateur par leur plus grand commun diviseur (plutôt que par un quelconque diviseur commun).

Comment réduire une fraction ? Règles et exemples de fractions réductrices

Il ne reste plus qu'à regarder la règle de réduction des fractions, qui explique comment réduire une fraction donnée.

Règle de réduction des fractions se compose de deux étapes :

• tout d'abord, le pgcd du numérateur et du dénominateur de la fraction est trouvé ;
• deuxièmement, le numérateur et le dénominateur de la fraction sont divisés par leur pgcd, ce qui donne une fraction irréductible égale à celle d'origine.

Faisons le tri exemple de réduction d'une fraction selon la règle énoncée.

www.cleverstudents.ru

Réduire les fractions. Que signifie réduire une fraction ?

La réduction de fractions est nécessaire pour réduire la fraction à une forme plus simple, par exemple dans la réponse obtenue à la suite de la résolution d'une expression.

Fractions réductrices, définition et formule.

Qu’est-ce que la réduction des fractions ? Que signifie réduire une fraction ?

Définition:
Réduire les fractions- c'est la division du numérateur et du dénominateur d'une fraction par le même nombre positif différent de zéro et un. À la suite de la réduction, on obtient une fraction avec un numérateur et un dénominateur plus petits, égale à la fraction précédente selon la propriété principale nombres rationnels.

Formule pour réduire les fractions propriétés fondamentales des nombres rationnels.

Regardons un exemple :
Réduire la fraction \(\frac \)

Solution:
Nous pouvons factoriser une fraction en facteurs premiers et annuler les facteurs communs.

Réponse : après réduction, nous obtenons la fraction \(\frac\). Selon la propriété fondamentale des nombres rationnels, les fractions originales et résultantes sont égales.

Comment réduire des fractions ? Réduire une fraction à sa forme irréductible.

Pour obtenir une fraction irréductible, il faut trouver le plus grand diviseur commun (PGCD) pour le numérateur et le dénominateur de la fraction.

Il existe plusieurs façons de trouver GCD ; dans l'exemple, nous utiliserons la décomposition des nombres en facteurs premiers.

Obtenez la fraction irréductible \(\frac\).

Solution:
Trouvons GCD(48, 136). Écrivons les nombres 48 et 136 en facteurs premiers.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
PGCD(48, 136)= 2⋅2⋅2=6

La règle pour réduire une fraction à une forme irréductible.

1. Vous devez trouver le plus grand commun diviseur du numérateur et du dénominateur.
2. Vous devez diviser le numérateur et le dénominateur par le plus grand diviseur commun pour obtenir une fraction irréductible suite à la division.

Exemple:
Réduisez la fraction \(\frac\).

Solution:
Trouvons GCD(152, 168). Écrivons les nombres 152 et 168 en facteurs premiers.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
PGCD(152, 168)= 2⋅2⋅2=6

Réponse : \(\frac \) est une fraction irréductible.

Réduire les fractions impropres.

Comment raccourcir fraction correcte?
Les règles de réduction des fractions sont les mêmes pour les fractions propres et impropres.

Regardons un exemple :
Réduisez la fraction impropre \(\frac\).

Solution:
Écrivons le numérateur et le dénominateur en facteurs simples. Et puis nous réduirons les facteurs communs.

Réduire les fractions mélangées.

Les fractions mixtes suivent les mêmes règles que les fractions ordinaires. La seule différence est que nous pouvons ne touchez pas la partie entière, mais réduisez la partie fractionnaire ou Convertissez une fraction mixte en fraction impropre, réduisez-la et reconvertissez-la en fraction propre.

Regardons un exemple :
Annulez la fraction mixte \(2\frac\).

Solution:
Résolvons-le de deux manières :
Première façon :
Écrivons la partie fractionnaire en facteurs simples, mais nous n'aborderons pas la partie entière.

Deuxième manière :
Convertissons-le d'abord en fraction impropre, puis écrivons-le en facteurs premiers et réduisons-le. Convertissons la fraction impropre résultante en une fraction propre.

Questions connexes:
Pouvez-vous réduire des fractions lors de l’addition ou de la soustraction ?
Réponse : non, vous devez d'abord ajouter ou soustraire des fractions selon les règles, puis les réduire seulement. Regardons un exemple :

Solution:
Ils font souvent l’erreur de réduire les mêmes nombres au numérateur et au dénominateur, dans notre cas le nombre 20, mais ils ne peuvent être réduits que lorsque vous avez terminé l’addition et la soustraction.

De quels nombres pouvez-vous réduire une fraction ?
Réponse : Vous pouvez réduire une fraction du plus grand commun diviseur ou du commun diviseur du numérateur et du dénominateur. Par exemple, la fraction \(\frac \).

Écrivons les nombres 100 et 150 en facteurs premiers.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Le plus grand diviseur commun sera le nombre pgcd(100, 150)= 2⋅5⋅5=50

Nous avons la fraction irréductible \(\frac \).

Mais il n'est pas toujours nécessaire de diviser par pgcd ; une fraction irréductible n'est pas toujours nécessaire ; vous pouvez réduire la fraction par un simple diviseur du numérateur et du dénominateur. Par exemple, les nombres 100 et 150 ont un diviseur commun de 2. Réduisons la fraction \(\frac \) de 2.

Nous avons la fraction réductible \(\frac\).

Quelles fractions peuvent être réduites ?
Réponse : Vous pouvez réduire les fractions dont le numérateur et le dénominateur ont un diviseur commun. Par exemple, la fraction \(\frac \). Les nombres 4 et 8 ont un nombre par lequel ils sont tous deux divisibles - le nombre 2. Par conséquent, une telle fraction peut être réduite du nombre 2.

Exemple:
Comparez les deux fractions \(\frac \) et \(\frac \).

Ces deux fractions sont égales. Regardons de plus près la fraction \(\frac \) :

Deux fractions sont égales si et seulement si l’une d’elles est obtenue en réduisant l’autre fraction par le facteur commun du numérateur et du dénominateur.

Exemple:
Réduisez si possible les fractions suivantes : a) \(\frac \) b) \(\frac \) c) \(\frac \) d) \(\frac \)

Opérations avec des fractions ordinaires

Expansion des fractions. Réduire une fraction. Comparer des fractions.

Réduction à un dénominateur commun. Addition et soustraction fractions

Multiplier des fractions. Division de fractions .

Expansion des fractions. La valeur d'une fraction ne change pas si vous multipliez son numérateur et son dénominateur par le même nombre autre que zéro. expansion d'une fraction. Par exemple,



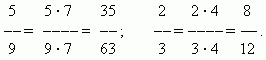
Réduire une fraction. La valeur d'une fraction ne change pas si vous divisez son numérateur et son dénominateur par le même nombre autre que zéro.. Cette transformation est appelée réduire une fraction. Par exemple,



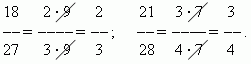
Comparer des fractions. De deux fractions ayant les mêmes numérateurs, celle dont le dénominateur est le plus petit est la plus grande :



De deux fractions de même dénominateur, celle dont le numérateur est le plus grand est la plus grande :



Pour comparer des fractions ayant des numérateurs et des dénominateurs différents, vous devez les développer pour les amener à un dénominateur commun.

EXEMPLE Comparez deux fractions :

Développons la première fraction par le dénominateur de la seconde, et la seconde par le dénominateur de la première :

La transformation utilisée ici s'appelle amener les fractions à un dénominateur commun.

Additionner et soustraire des fractions. Si les dénominateurs des fractions sont les mêmes, alors pour additionner les fractions, vous devez ajouter leurs numérateurs, et pour soustraire les fractions, vous devez soustraire leurs numérateurs (dans le même ordre). La somme ou la différence résultante sera le numérateur du résultat ; le dénominateur restera le même. Si les dénominateurs des fractions sont différents, vous devez d'abord réduire les fractions à un dénominateur commun. Lors de l'ajout de nombres fractionnaires, leurs parties entières et fractionnaires sont ajoutées séparément. Lors de la soustraction de nombres fractionnaires, nous vous recommandons de les convertir d'abord en fractions impropres, puis de soustraire l'une de l'autre, puis de reconvertir le résultat, si nécessaire, sous forme de nombres fractionnaires.



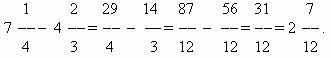
Multiplier des fractions. Multiplier un nombre par une fraction signifie le multiplier par le numérateur et diviser le produit par le dénominateur. Nous avons donc règle générale multiplier des fractions : pour multiplier des fractions, vous devez multiplier leurs numérateurs et dénominateurs séparément et diviser le premier produit par le second.

EXEMPLE

Diviser des fractions. Pour diviser un nombre par une fraction, vous devez multiplier ce nombre par la fraction réciproque. Cette règle découle de la définition de la division (voir la section « Opérations arithmétiques »).

EXEMPLE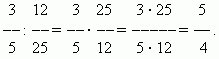

Multiplier et diviser des fractions

La dernière fois, nous avons appris à additionner et à soustraire des fractions (voir la leçon « Additionner et soustraire des fractions »). La partie la plus difficile de ces actions consistait à amener les fractions à un dénominateur commun.

Il est maintenant temps de s'occuper de la multiplication et de la division. Bonnes nouvelles est que ces opérations sont encore plus simples que l’addition et la soustraction. Considérons d’abord le cas le plus simple, lorsqu’il existe deux fractions positives sans partie entière séparée.

Pour multiplier deux fractions, vous devez multiplier leurs numérateurs et dénominateurs séparément. Le premier nombre sera le numérateur de la nouvelle fraction et le second sera le dénominateur.

Pour diviser deux fractions, vous devez multiplier la première fraction par la deuxième fraction « inversée ».

De la définition, il résulte que la division de fractions se réduit à la multiplication. Pour « retourner » une fraction, échangez simplement le numérateur et le dénominateur. Par conséquent, tout au long de la leçon, nous considérerons principalement la multiplication.

À la suite de la multiplication, une fraction réductible peut apparaître (et apparaît souvent) - elle doit bien sûr être réduite. Si après toutes les réductions la fraction s'avère incorrecte, la partie entière doit être mise en évidence. Mais ce qui n'arrivera certainement pas avec la multiplication, c'est la réduction à un dénominateur commun : pas de méthodes croisées, de plus grands facteurs et de plus petits multiples communs.



Multiplier des fractions par des parties entières et des fractions négatives

Si les fractions contiennent une partie entière, elles doivent être converties en fractions impropres - et ensuite seulement multipliées selon les schémas décrits ci-dessus.

S'il y a un moins au numérateur d'une fraction, au dénominateur ou devant celui-ci, il peut être retiré de la multiplication ou supprimé complètement selon les règles suivantes :

1. Plus par moins donne moins ;
2. Deux négatifs font un affirmatif.

Jusqu'à présent, ces règles n'étaient rencontrées que lors de l'addition et de la soustraction de fractions négatives, lorsqu'il fallait se débarrasser de la partie entière. Pour un ouvrage, ils peuvent être généralisés afin de « brûler » plusieurs inconvénients à la fois :

3. On raye les négatifs par paires jusqu'à ce qu'ils disparaissent complètement. Dans des cas extrêmes, un moins peut survivre - celui pour lequel il n'y avait pas de partenaire ;
4. S'il ne reste plus de points négatifs, l'opération est terminée - vous pouvez commencer à multiplier. Si le dernier moins n’est pas barré parce qu’il n’y avait pas de paire, on le sort des limites de la multiplication. Le résultat est une fraction négative.

Tâche. Trouvez le sens de l'expression :

Nous convertissons toutes les fractions en fractions impropres, puis retirons les moins de la multiplication. On multiplie ce qui reste selon les règles habituelles. On a:



Permettez-moi de vous rappeler encore une fois que le moins qui apparaît devant une fraction avec une partie entière en surbrillance fait spécifiquement référence à la fraction entière, et pas seulement à sa partie entière (cela s'applique aux deux derniers exemples).

Notez également nombres négatifs: Lors de la multiplication, ils sont mis entre parenthèses. Ceci est fait afin de séparer les moins des signes de multiplication et de rendre l'ensemble de la notation plus précise.

Réduire les fractions à la volée

La multiplication est une opération très laborieuse. Les nombres ici s'avèrent assez grands, et pour simplifier le problème, vous pouvez essayer de réduire davantage la fraction avant la multiplication. En effet, par essence, les numérateurs et les dénominateurs des fractions sont des facteurs ordinaires et, par conséquent, ils peuvent être réduits en utilisant la propriété fondamentale d'une fraction. Jetez un œil aux exemples :



Par définition nous avons :



Dans tous les exemples, les nombres réduits et ce qui en reste sont marqués en rouge.

Attention : dans le premier cas, les multiplicateurs ont été complètement réduits. A leur place restent des unités qui, en général, n'ont pas besoin d'être écrites. Dans le deuxième exemple, il n’a pas été possible d’obtenir une réduction complète, mais le montant total des calculs a néanmoins diminué.

Cependant, n’utilisez jamais cette technique pour additionner et soustraire des fractions ! Oui, il existe parfois des chiffres similaires que vous souhaitez simplement réduire. Tiens, regarde :

Vous ne pouvez pas faire ça !

L'erreur se produit car lors de l'addition, le numérateur d'une fraction produit une somme et non un produit de nombres. Par conséquent, il est impossible d’appliquer la propriété fondamentale d’une fraction, puisque cette propriété concerne spécifiquement la multiplication des nombres.

Il n'y a tout simplement aucune autre raison pour réduire les fractions, donc la bonne solution au problème précédent ressemble à ceci :

Comme vous pouvez le constater, la bonne réponse s’est avérée moins belle. En général, soyez prudent.

Cet article continue le sujet de la conversion de fractions algébriques : considérons une action telle que la réduction de fractions algébriques. Définissons le terme lui-même, formulons une règle de réduction et analysons des exemples pratiques.

Yandex.RTB R-A-339285-1

La signification de réduire une fraction algébrique

Dans les documents sur les fractions communes, nous avons examiné sa réduction. Nous avons défini la réduction d'une fraction comme la division de son numérateur et de son dénominateur par un facteur commun.

Réduire une fraction algébrique est une opération similaire.

Définition 1

Réduire une fraction algébrique est la division de son numérateur et de son dénominateur par un facteur commun. Dans ce cas, contrairement à la réduction d'une fraction ordinaire (le dénominateur commun ne peut être qu'un nombre), le facteur commun du numérateur et du dénominateur d'une fraction algébrique peut être un polynôme, notamment un monôme ou un nombre.

Par exemple, la fraction algébrique 3 x 2 + 6 x y 6 x 3 y + 12 x 2 y 2 peut être réduite du nombre 3, ce qui donne : x 2 + 2 x y 6 x 3 · y + 12 · x 2 · y 2 . Nous pouvons réduire la même fraction par la variable x, et cela nous donnera l'expression 3 x + 6 y 6 x 2 y + 12 x y 2. Il est également possible de réduire une fraction donnée par un monôme 3x ou l'un des polynômes x + 2 ans, 3 x + 6 oui , x 2 + 2 x oui ou 3 x 2 + 6 x y.

Le but ultime de la réduction d’une fraction algébrique est d’obtenir une fraction d’une forme plus simple, au mieux une fraction irréductible.

Toutes les fractions algébriques sont-elles sujettes à réduction ?

Encore une fois, à partir de matériaux sur des fractions ordinaires, nous savons qu'il existe des fractions réductibles et irréductibles. Les fractions irréductibles sont des fractions qui n'ont pas de facteurs communs au numérateur et au dénominateur autres que 1.

C’est la même chose avec les fractions algébriques : elles peuvent avoir des facteurs communs au numérateur et au dénominateur, ou non. La présence de facteurs communs permet de simplifier la fraction originale par réduction. Lorsqu’il n’y a pas de facteurs communs, il est impossible d’optimiser une fraction donnée par la méthode de réduction.

Dans les cas généraux, étant donné le type de fraction, il est assez difficile de comprendre si elle peut être réduite. Bien entendu, dans certains cas, la présence d’un facteur commun entre le numérateur et le dénominateur est évidente. Par exemple, dans la fraction algébrique 3 x 2 3 y, il est clair que le facteur commun est le nombre 3.

Dans la fraction - x · y 5 · x · y · z 3 on comprend aussi immédiatement qu'elle peut être réduite de x, ou y, ou x · y. Et pourtant, il existe bien plus souvent des exemples de fractions algébriques, où le facteur commun du numérateur et du dénominateur n'est pas si facile à voir, et encore plus souvent, il est tout simplement absent.

Par exemple, nous pouvons réduire la fraction x 3 - 1 x 2 - 1 de x - 1, alors que le facteur commun spécifié n'est pas présent dans l'entrée. Mais la fraction x 3 - x 2 + x - 1 x 3 + x 2 + 4 · x + 4 ne peut pas être réduite, puisque le numérateur et le dénominateur n'ont pas de facteur commun.

Ainsi, la question de déterminer la réductibilité d'une fraction algébrique n'est pas si simple, et il est souvent plus facile de travailler avec une fraction d'une forme donnée que d'essayer de savoir si elle est réductible. Dans ce cas, de telles transformations ont lieu qui permettent dans des cas particuliers de déterminer le facteur commun du numérateur et du dénominateur ou de tirer une conclusion sur l'irréductibilité d'une fraction. Nous examinerons cette question en détail dans le prochain paragraphe de l'article.

Règle de réduction des fractions algébriques

Règle de réduction des fractions algébriques se compose de deux actions séquentielles :

• trouver les facteurs communs du numérateur et du dénominateur ;
• s'il y en a, l'action de réduction de la fraction est réalisée directement.

La méthode la plus pratique pour trouver des dénominateurs communs consiste à factoriser les polynômes présents dans le numérateur et le dénominateur d’une fraction algébrique donnée. Cela vous permet de voir immédiatement et clairement la présence ou l'absence de facteurs communs.

L'action même de réduire une fraction algébrique repose sur la propriété principale d'une fraction algébrique, exprimée par l'égalité indéfinie, où a, b, c sont des polynômes et b et c sont non nuls. La première étape consiste à réduire la fraction à la forme a · c b · c, dans laquelle on remarque immédiatement le facteur commun c. La deuxième étape consiste à effectuer une réduction, c'est-à-dire transition vers une fraction de la forme a b .

Exemples typiques

Malgré quelques évidences, clarifions cas particulier lorsque le numérateur et le dénominateur d'une fraction algébrique sont égaux. Les fractions similaires sont identiquement égales à 1 sur l'ensemble de l'ODZ des variables de cette fraction :

5 5 = 1 ; - 2 3 - 2 3 = 1 ; xx = 1 ; - 3, 2 x 3 - 3, 2 x 3 = 1 ; 1 2 · x - x 2 · y 1 2 · x - x 2 · y ;

Les fractions ordinaires étant un cas particulier des fractions algébriques, rappelons comment elles se réduisent. Les nombres naturels écrits au numérateur et au dénominateur sont pris en compte en facteurs premiers, puis les facteurs communs sont annulés (le cas échéant).

Par exemple, 24 1 260 = 2 2 2 3 2 2 3 3 5 7 = 2 3 5 7 = 2 105

Le produit de facteurs simples et identiques peut être écrit sous forme de puissances et, dans le processus de réduction d'une fraction, utiliser la propriété de diviser des puissances avec des bases identiques. Alors la solution ci-dessus serait :

24 1260 = 2 3 3 2 2 3 2 5 7 = 2 3 - 2 3 2 - 1 5 7 = 2 105

(numérateur et dénominateur divisés par un facteur commun 2 2 3). Ou pour plus de clarté, en fonction des propriétés de multiplication et de division, nous donnons à la solution la forme suivante :

24 1260 = 2 3 3 2 2 3 2 5 7 = 2 3 2 2 3 3 2 1 5 7 = 2 1 1 3 1 35 = 2 105

Par analogie, on effectue la réduction de fractions algébriques, dans lesquelles le numérateur et le dénominateur ont des monômes à coefficients entiers.

Exemple 1

La fraction algébrique est donnée - 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z. Il faut le réduire.

Solution

Il est possible d'écrire le numérateur et le dénominateur d'une fraction donnée comme un produit de facteurs et de variables simples, puis d'effectuer la réduction :

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = - 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · c · z = = - 3 · 3 · a · a · a 2 · c · c · c · c · c · c = - 9 une 3 2 c 6

Cependant, une manière plus rationnelle serait d’écrire la solution sous la forme d’une expression avec des puissances :

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = - 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = - 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = - 3 3 - 1 2 · a 5 - 2 1 · 1 · 1 c 7 - 1 · 1 = · - 3 2 · une 3 2 · c 6 = · - 9 · une 3 2 · c 6 .

Répondre:- 27 une 5 b 2 c z 6 une 2 b 2 c 7 z = - 9 une 3 2 c 6

Lorsque le numérateur et le dénominateur d'une fraction algébrique contiennent des coefficients numériques fractionnaires, il existe deux manières possibles d'agir : soit diviser ces coefficients fractionnaires séparément, soit d'abord se débarrasser des coefficients fractionnaires en multipliant le numérateur et le dénominateur par un nombre naturel. La dernière transformation est effectuée en raison de la propriété fondamentale d'une fraction algébrique (vous pouvez en lire plus dans l'article « Réduire une fraction algébrique à un nouveau dénominateur »).

Exemple 2

La fraction donnée est 2 5 x 0, 3 x 3. Il faut le réduire.

Solution

Il est possible de réduire la fraction de cette façon :

2 5 x 0, 3 x 3 = 2 5 3 10 x x 3 = 4 3 1 x 2 = 4 3 x 2

Essayons de résoudre le problème différemment, après nous être débarrassés des coefficients fractionnaires - multiplions le numérateur et le dénominateur par le plus petit commun multiple des dénominateurs de ces coefficients, c'est-à-dire sur LCM (5, 10) = 10. On obtient alors :

2 5 x 0, 3 x 3 = 10 2 5 x 10 0, 3 x 3 = 4 x 3 x 3 = 4 3 x 2.

Réponse : 2 5 x 0, 3 x 3 = 4 3 x 2

Quand on réduit des fractions algébriques vue générale, dans lequel les numérateurs et les dénominateurs peuvent être soit des monômes, soit des polynômes, il peut y avoir un problème lorsque le facteur commun n'est pas toujours immédiatement visible. Ou d’ailleurs, cela n’existe tout simplement pas. Ensuite, pour déterminer le facteur commun ou enregistrer le fait de son absence, le numérateur et le dénominateur de la fraction algébrique sont factorisés.

Exemple 3

La fraction rationnelle 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 - 49 · b 3 est donnée. Il faut le réduire.

Solution

Factorisons les polynômes au numérateur et au dénominateur. Mettons-le entre parenthèses :

2 une 2 b 2 + 28 une b 2 + 98 b 2 une 2 b 3 - 49 b 3 = 2 b 2 (une 2 + 14 une + 49) b 3 (une 2 - 49)

On voit que l'expression entre parenthèses peut être convertie à l'aide de formules de multiplication abrégées :

2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49) = 2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7)

On voit bien qu'il est possible de réduire une fraction d'un facteur commun b 2 (a + 7). Faisons une réduction :

2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7) = 2 (a + 7) b (a - 7) = 2 a + 14 a b - 7 b

Écrivons une solution courte sans explication sous la forme d'une chaîne d'égalités :

2 une 2 b 2 + 28 une b 2 + 98 b 2 une 2 b 3 - 49 b 3 = 2 b 2 (une 2 + 14 une + 49) b 3 (une 2 - 49) = = 2 b 2 (une + 7) 2 b 3 (a - 7) (a + 7) = 2 (a + 7) b (a - 7) = 2 a + 14 a b - 7 b

Répondre: 2 une 2 b 2 + 28 une b 2 + 98 b 2 une 2 b 3 - 49 b 3 = 2 une + 14 une b - 7 b.

Il arrive que des facteurs communs soient masqués par des coefficients numériques. Ensuite, lors de la réduction de fractions, il est optimal de mettre entre parenthèses les facteurs numériques aux puissances supérieures du numérateur et du dénominateur.

Exemple 4

Étant donné la fraction algébrique 1 5 · x - 2 7 · x 3 · y 5 · x 2 · y - 3 1 2 . Il faut le réduire si possible.

Solution

À première vue, le numérateur et le dénominateur n’ont pas de dénominateur commun. Cependant, essayons de convertir la fraction donnée. Retirons le facteur x au numérateur :

1 5 x - 2 7 x 3 oui 5 x 2 oui - 3 1 2 = x 1 5 - 2 7 x 2 oui 5 x 2 oui - 3 1 2

Vous pouvez maintenant voir une certaine similitude entre l'expression entre parenthèses et l'expression au dénominateur en raison de x 2 y . Retirons les coefficients numériques des puissances supérieures de ces polynômes :

x 1 5 - 2 7 x 2 y 5 x 2 y - 3 1 2 = x - 2 7 - 7 2 1 5 + x 2 y 5 x 2 y - 1 5 3 1 2 = = - 2 7 x - 7 10 + x 2 ans 5 x 2 ans - 7 10

Maintenant que le facteur commun devient visible, on effectue la réduction :

2 7 x - 7 10 + x 2 oui 5 x 2 oui - 7 10 = - 2 7 x 5 = - 2 35 x

Répondre: 1 5 x - 2 7 x 3 oui 5 x 2 oui - 3 1 2 = - 2 35 x .

Soulignons que l'habileté de contraction fractions rationnelles dépend de la capacité à factoriser des polynômes.

Si vous remarquez une erreur dans le texte, veuillez la surligner et appuyer sur Ctrl+Entrée

La calculatrice en ligne fonctionne réduction de fractions algébriques conformément à la règle des fractions réductrices : remplacer la fraction d'origine par une fraction égale, mais avec un numérateur et un dénominateur plus petits, c'est-à-dire Diviser simultanément le numérateur et le dénominateur d'une fraction par leur plus grand facteur commun (PGCD). La calculatrice affiche également une solution détaillée qui vous aidera à comprendre la séquence de réduction.

Donné:

Solution:

Effectuer une réduction de fraction

vérifier la possibilité d'effectuer une réduction de fraction algébrique

1) Détermination du plus grand diviseur commun (PGCD) du numérateur et du dénominateur d'une fraction

déterminer le plus grand commun diviseur (PGCD) du numérateur et du dénominateur d'une fraction algébrique

2) Réduire le numérateur et le dénominateur d'une fraction

réduire le numérateur et le dénominateur d'une fraction algébrique

3) Sélection de la partie entière d'une fraction

séparer la partie entière d'une fraction algébrique

4) Conversion d'une fraction algébrique en fraction décimale

convertir une fraction algébrique en décimal

Aide au développement du site internet du projet

Cher visiteur du site.
Si vous n'avez pas trouvé ce que vous cherchiez, assurez-vous d'écrire dans les commentaires ce qui manque actuellement sur le site. Cela nous aidera à comprendre dans quelle direction nous devons aller plus loin, et d'autres visiteurs pourront bientôt recevoir le matériel nécessaire.
Si le site s'est avéré utile, faites don du site au projet seulement 2 ₽ et nous saurons que nous allons dans la bonne direction.

Merci pour la visite!

I. Procédure de réduction d'une fraction algébrique à l'aide d'une calculatrice en ligne :

1. Pour réduire une fraction algébrique, saisissez les valeurs du numérateur et du dénominateur de la fraction dans les champs appropriés. Si la fraction est mixte, remplissez également le champ correspondant à la partie entière de la fraction. Si la fraction est simple, laissez le champ de la partie entière vide.
2. Pour spécifier une fraction négative, placez un signe moins sur toute la partie de la fraction.
3. En fonction de la fraction algébrique spécifiée, la séquence d'actions suivante est automatiquement effectuée :

• déterminer le plus grand diviseur commun (PGCD) du numérateur et du dénominateur d'une fraction;
• réduire le numérateur et le dénominateur d'une fraction par pgcd;
• mettre en évidence la partie entière d'une fraction, si le numérateur de la fraction finale est supérieur au dénominateur.
• convertir la fraction algébrique finale en fraction décimale arrondi au centième le plus proche.

II. Pour référence:

Une fraction est un nombre composé d'une ou plusieurs parties (fractions) d'une unité. Fraction commune(fraction simple) s'écrit sous la forme de deux nombres (le numérateur de la fraction et le dénominateur de la fraction) séparés par une barre horizontale (la barre de fraction) indiquant le signe de division. Le numérateur d'une fraction est le nombre situé au-dessus de la ligne de fraction. Le numérateur indique combien de parts ont été prélevées sur l'ensemble. Le dénominateur d'une fraction est le nombre situé sous la ligne de fraction. Le dénominateur indique en combien de parties égales le tout est divisé. Une fraction simple est une fraction qui ne comporte pas de partie entière. Une fraction simple peut être propre ou impropre. Une fraction propre est une fraction dont le numérateur est inférieur à son dénominateur, donc une fraction propre est toujours inférieure à un. Exemple de fractions propres : 8/7, 11/19, 16/17. Une fraction impropre est une fraction dans laquelle le numérateur est supérieur ou égal au dénominateur, donc une fraction impropre est toujours supérieure ou égale à un. Exemple de fractions impropres : 7/6, 8/7, 13/13. une fraction mixte est un nombre qui contient un nombre entier et une fraction propre, et désigne la somme de ce nombre entier et de la fraction propre. Toute fraction mixte peut être convertie en fraction impropre fraction simple. Exemple de fractions mixtes : 1¼, 2½, 4¾.

III. Note:

1. Le bloc de données source est surligné en jaune, bloc de calcul intermédiaire attribué bleu , le bloc de solution est surligné en vert.
2. Pour additionner, soustraire, multiplier et diviser des fractions ordinaires ou mixtes, utilisez le calculateur de fractions en ligne avec solution détaillée.

Ainsi, nous savons déjà que le numérateur et le dénominateur d'une fraction peuvent être multipliés et divisés par le même nombre, la fraction ne changera pas. Considérons trois approches :

Approchez-en un.

Pour réduire, divisez le numérateur et le dénominateur par un diviseur commun. Regardons des exemples :

Raccourcissons :

Dans les exemples donnés, on voit immédiatement quels diviseurs prendre pour la réduction. Le processus est simple : nous passons par 2,3,4,5 et ainsi de suite. Dans la plupart des exemples de cours scolaires, cela suffit amplement. Mais si c'est une fraction :

Ici, le processus de sélection des diviseurs peut prendre beaucoup de temps ;). Bien sûr, de tels exemples ne font pas partie du programme scolaire, mais il faut être capable d'y faire face. Ci-dessous, nous verrons comment cela se fait. Pour l'instant, revenons au processus de réduction des effectifs.

Comme indiqué ci-dessus, afin de réduire une fraction, nous avons divisé par le(s) diviseur(s) commun(s) que nous avons déterminé. Tout est correct! Il suffit d'ajouter des signes de divisibilité des nombres :

- si le nombre est pair, alors il est divisible par 2.

- si un nombre composé des deux derniers chiffres est divisible par 4, alors le nombre lui-même est divisible par 4.

— si la somme des chiffres qui composent le nombre est divisible par 3, alors le nombre lui-même est divisible par 3. Par exemple, 125031, 1+2+5+0+3+1=12. Douze est divisible par 3, donc 123031 est divisible par 3.

- si le nombre se termine par 5 ou 0, alors le nombre est divisible par 5.

— si la somme des chiffres qui composent le nombre est divisible par 9, alors le nombre lui-même est divisible par 9. Par exemple, 625032 =.> 6+2+5+0+3+2=18. Dix-huit est divisible par 9, ce qui signifie que 623032 est divisible par 9.

Deuxième approche.

Pour le dire brièvement, en fait, toute l'action se résume à factoriser le numérateur et le dénominateur puis à réduire des facteurs égaux au numérateur et au dénominateur (cette approche est une conséquence de la première approche) :

Visuellement, afin d'éviter toute confusion et erreur, les facteurs égaux sont simplement barrés. Question : comment factoriser un nombre ? Il est nécessaire de déterminer tous les diviseurs par recherche. C'est un sujet à part, ce n'est pas compliqué, recherchez les informations dans un manuel ou sur Internet. Vous ne rencontrerez pas de gros problèmes avec la factorisation des nombres présents dans les fractions scolaires.

Formellement, le principe de réduction peut s’écrire comme suit :

Approchez-en trois.

Voici la chose la plus intéressante pour les avancés et ceux qui veulent le devenir. Réduisons la fraction 143/273. Essayez-le vous-même ! Eh bien, comment est-ce arrivé rapidement ? Maintenant regarde !

On le retourne (on change les places du numérateur et du dénominateur). Nous divisons la fraction résultante par un coin et la convertissons en un nombre fractionnaire, c'est-à-dire que nous sélectionnons la partie entière :

C'est déjà plus facile. On voit que le numérateur et le dénominateur peuvent être réduits par 13 :

Maintenant, n'oubliez pas de retourner la fraction, écrivons toute la chaîne :

Vérifié - cela prend moins de temps que de rechercher et de vérifier les diviseurs. Revenons à nos deux exemples :

D'abord. En divisant avec un coin (pas sur une calculatrice), on obtient :

Cette fraction est bien sûr plus simple, mais la réduction pose encore une fois un problème. Maintenant, nous analysons séparément la fraction 1273/1463 et la retournons :

C'est plus facile ici. On peut considérer un diviseur tel que 19. Le reste ne convient pas, c'est clair : 190 :19 = 10, 1273 :19 = 67. Hourra ! Écrivons :

Exemple suivant. Raccourcissons 88179/2717.

Divisons, on obtient :

Séparément, nous analysons la fraction 1235/2717 et la retournons :

On peut considérer un diviseur tel que 13 (jusqu'à 13 ne convient pas) :

Numérateur 247:13=19 Dénominateur 1235:13=95

*Au cours du processus, nous avons vu un autre diviseur égal à 19. Il s'avère que :

Maintenant, nous notons le numéro d'origine :

Et peu importe ce qui est le plus grand dans la fraction - le numérateur ou le dénominateur, si c'est le dénominateur, alors nous le retournons et agissons comme décrit. De cette façon, nous pouvons réduire n'importe quelle fraction ; la troisième approche peut être qualifiée d'universelle.

Bien entendu, les deux exemples évoqués ci-dessus ne sont pas des exemples simples. Essayons cette technologie sur les fractions « simples » que nous avons déjà envisagées :

Deux quarts.

Soixante-douze années soixante. Le numérateur est supérieur au dénominateur, il n'est pas nécessaire de l'inverser :

Bien entendu, la troisième approche a été appliquée à de tels exemples simples juste comme alternative. La méthode, comme déjà dit, est universelle, mais pas pratique ni correcte pour toutes les fractions, en particulier les plus simples.

La variété des fractions est grande. Il est important que vous compreniez les principes. Règles strictes il n'y a tout simplement aucun moyen de travailler avec des fractions. Nous avons regardé, compris comment il serait plus pratique d'agir et sommes allés de l'avant. Avec la pratique, l’habileté viendra et vous les casserez comme des graines.

Conclusion:

Si vous voyez un ou plusieurs diviseurs communs pour le numérateur et le dénominateur, utilisez-les pour réduire.

Si vous savez comment factoriser rapidement un nombre, factorisez le numérateur et le dénominateur, puis réduisez.

Si vous ne parvenez pas à déterminer le diviseur commun, utilisez la troisième approche.

*Pour réduire des fractions, il est important de maîtriser les principes de réduction, de comprendre la propriété de base d'une fraction, de connaître les approches de résolution et d'être extrêmement prudent lors des calculs.

Et rappelez-vous! Il est d'usage de réduire une fraction jusqu'à ce qu'elle s'arrête, c'est-à-dire de la réduire tant qu'il existe un diviseur commun.

Cordialement, Alexandre Krutitskikh.