Väärien murtolukujen vähentäminen. Online-laskin algebrallisten murtolukujen vähentämiseen yksityiskohtaisella ratkaisulla antaa sinun pienentää murto-osaa ja muuntaa väärän murtoluvun oikeaksi murtoluvuksi

Jos joudumme jakamaan 497 4:llä, niin jakamalla näemme, että 497 ei ole tasaisesti jaollinen 4:llä, ts. loput divisioonasta jää. Tällaisissa tapauksissa sanotaan, että se on valmis jako jäännöksellä, ja ratkaisu kirjoitetaan seuraavasti:
497: 4 = 124 (1 loppu).

Jakokomponentteja tasa-arvon vasemmalla puolella kutsutaan samoin kuin jaossa ilman jäännöstä: 497 - osinkoa, 4 - jakaja. Jakotulosta, kun jaetaan jäännöksellä, kutsutaan epätäydellinen yksityinen. Meidän tapauksessamme tämä on numero 124. Ja lopuksi viimeinen komponentti, joka ei ole tavallisessa jaossa, on loput. Tapauksissa, joissa ei ole jäännöstä, yhden luvun sanotaan jaettuna toisella ilman jälkiä tai kokonaan. Uskotaan, että tällaisella jaolla jäännös on nolla. Meidän tapauksessamme jäännös on 1.

Jäännös on aina pienempi kuin jakaja.

Jako voidaan tarkistaa kertolaskulla. Jos esimerkiksi on yhtälö 64: 32 = 2, niin tarkistus voidaan tehdä näin: 64 = 32 * 2.

Usein tapauksissa, joissa jako jäännöksellä suoritetaan, on kätevää käyttää tasa-arvoa
a = b * n + r,
missä a on osinko, b on jakaja, n on osaosamäärä, r on jäännös.

Luonnollisten lukujen osamäärä voidaan kirjoittaa murtolukuna.

Murtoluvun osoittaja on osinko, ja nimittäjä on jakaja.

Koska murtoluvun osoittaja on osinko ja nimittäjä jakaja, uskovat, että murto-osan viiva tarkoittaa jakolaskua. Joskus on kätevää kirjoittaa jako murtolukuna ilman ":"-merkkiä.

Luonnollisten lukujen m ja n jaon osamäärä voidaan kirjoittaa murtolukuna \(\frac(m)(n) \), jossa osoittaja m on osinko ja nimittäjä n on jakaja:
\(m:n = \frac(m)(n) \)

Seuraavat säännöt pitävät paikkansa:

Saadaksesi murtoluvun \(\frac(m)(n)\), sinun on jaettava yksi n:llä yhtä suuret osat(osakkeita) ja ota m tällaisia ​​osia.

Saadaksesi murtoluvun \(\frac(m)(n)\), sinun on jaettava luku m luvulla n.

Jos haluat löytää kokonaisuuden osan, sinun on jaettava kokonaisuutta vastaava luku nimittäjällä ja kerrottava tulos tämän osan ilmaisevan murto-osan osoittajalla.

Jos haluat löytää kokonaisuuden osasta, sinun on jaettava tätä osaa vastaava luku osoittajalla ja kerrottava tulos tämän osan ilmaisevan murto-osan nimittäjällä.

Jos murto-osan osoittaja ja nimittäjä kerrotaan samalla luvulla (paitsi nolla), murto-osan arvo ei muutu:
\(\suuri \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)

Jos murto-osan osoittaja ja nimittäjä jaetaan samalla luvulla (paitsi nolla), murto-osan arvo ei muutu:
\(\suuri \frac(a)(b) = \frac(a: m)(b: m) \)
Tätä ominaisuutta kutsutaan murto-osan pääominaisuus.

Kaksi viimeistä muunnosa kutsutaan pienentää murto-osaa.

Jos murtoluvut on esitettävä murtoluvuina, joilla on sama nimittäjä, tätä toimintoa kutsutaan murto-osien vähentäminen yhteiseksi nimittäjäksi.

Oikeat ja väärät murtoluvut. Sekanumerot

Tiedät jo, että murto-osa voidaan saada jakamalla kokonaisuus yhtä suuriin osiin ja ottamalla useita tällaisia ​​osia. Esimerkiksi murto-osa \(\frac(3)(4)\) tarkoittaa kolmea neljäsosaa ykköstä. Monissa edellisen kappaleen ongelmissa murtolukuja käytettiin edustamaan kokonaisuuden osia. Maalaisjärkeä ehdottaa, että osan tulisi aina olla pienempi kuin kokonaisuus, mutta entä sitten murtoluvut, kuten esimerkiksi \(\frac(5)(5)\) tai \(\frac(8)(5)\)? On selvää, että tämä ei ole enää osa yksikköä. Luultavasti tästä syystä kutsutaan murtolukuja, joiden osoittaja on suurempi tai yhtä suuri kuin nimittäjä vääriä murtolukuja. Jäljelle jääneet murtoluvut eli murtoluvut, joiden osoittaja on pienempi kuin nimittäjä, kutsutaan oikeat murtoluvut.

Kuten tiedät, mikä tahansa yhteinen murtoluku, sekä oikea että väärä, voidaan ajatella tuloksena jakamalla osoittaja nimittäjällä. Siksi matematiikassa, toisin kuin tavallisessa kielessä, termi "virheellinen murtoluku" ei tarkoita, että teimme jotain väärin, vaan vain sitä, että tämän murtoluvun osoittaja on suurempi tai yhtä suuri kuin nimittäjä.

Jos luku koostuu kokonaisluvun osasta ja murto-osasta, niin sellainen fraktioita kutsutaan sekoitettuiksi.

Esimerkiksi:
\(5:3 = 1\frac(2)(3)\) : 1 - koko osa, ja \(\frac(2)(3)\) on murto-osa.

Jos murtoluvun \(\frac(a)(b)\) osoittaja on jaollinen luonnollinen luku n, sitten jakaaksesi tämän murtoluvun n:llä, sinun on jaettava sen osoittaja tällä numerolla:
\(\suuri \frac(a)(b) : n = \frac(a:n)(b) \)

Jos murtoluvun \(\frac(a)(b)\) osoittaja ei ole jaollinen luonnollisella luvulla n, jakaaksesi tämän murtoluvun n:llä, sinun on kerrottava sen nimittäjä tällä numerolla:
\(\suuri \frac(a)(b) : n = \frac(a)(bn) \)

Huomaa, että toinen sääntö on myös totta, kun osoittaja on jaollinen n:llä. Siksi voimme käyttää sitä silloin, kun on vaikea ensi silmäyksellä määrittää, onko murtoluvun osoittaja jaollinen n:llä vai ei.

Toiminnot murtoluvuilla. Murtolukujen lisääminen.

Voit suorittaa aritmeettisia operaatioita murtoluvuilla, aivan kuten luonnollisilla luvuilla. Katsotaanpa ensin murtolukujen lisäämistä. Murtolukuja on helppo lisätä samoilla nimittäjillä. Etsitään esimerkiksi \(\frac(2)(7)\) ja \(\frac(3)(7)\) summa. On helppo ymmärtää, että \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \)

Jos haluat lisätä murtolukuja, joilla on sama nimittäjä, sinun on lisättävä niiden osoittajat ja jätettävä nimittäjä ennalleen.

Kirjaimia käyttämällä sääntö samankaltaisten nimittäjien murtolukujen lisäämiseksi voidaan kirjoittaa seuraavasti:
\(\suuri \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)

Jos haluat lisätä murtolukuja eri nimittäjiä, niin ne on ensin saatava yhteiseksi nimittäjäksi. Esimerkiksi:
\(\suuri \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3) ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)

Murtoluvuille, kuten luonnollisille lukuille, yhteenlaskujen kommutatiiviset ja assosiatiiviset ominaisuudet ovat voimassa.

Lisää sekoitettuja fraktioita

Merkintöjä, kuten \(2\frac(2)(3)\) kutsutaan sekoitettuja fraktioita. Tässä tapauksessa kutsutaan numeroa 2 koko osa sekoitettu murtoluku, ja luku \(\frac(2)(3)\) on sen murto-osa. Merkintä \(2\frac(2)(3)\) luetaan seuraavasti: "kaksi ja kaksi kolmasosaa".

Kun jaat luvun 8 luvulla 3, saat kaksi vastausta: \(\frac(8)(3)\) ja \(2\frac(2)(3)\). Ne ilmaisevat saman murtoluvun, eli \(\frac(8)(3) = 2 \frac(2)(3)\)

Siten väärä murtoluku \(\frac(8)(3)\) esitetään sekamurtolukuna \(2\frac(2)(3)\). Tällaisissa tapauksissa he sanovat sen väärästä murto-osasta korosti koko osaa.

Murtolukujen vähentäminen (murtoluvut)

Vähennyslasku murtolukuja, kuten luonnolliset luvut, määräytyy summaustoiminnon perusteella: toisen vähentäminen yhdestä luvusta tarkoittaa sellaisen luvun löytämistä, joka toiseen lisättynä antaa ensimmäisen. Esimerkiksi:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) koska \(\frac(7)(9)+\frac(1)(9 ) = \frac(8)(9)\)

Samankaltaisten nimittäjien murtolukujen vähentämissääntö on samanlainen kuin tällaisten murtolukujen lisäämissääntö:
Jotta voit löytää eron samoilla nimittäjillä olevien murto-osien välillä, sinun on vähennettävä toisen osoittaja ensimmäisen murtoluvun osoittajasta ja jätettävä nimittäjä ennalleen.

Kirjaimia käyttämällä tämä sääntö kirjoitetaan seuraavasti:
\(\suuri \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)

Murtolukujen kertominen

Jos haluat kertoa murto-osan murtoluvulla, sinun on kerrottava niiden osoittajat ja nimittäjät ja kirjoitettava ensimmäinen tulo osoittajaksi ja toinen nimittäjäksi.

Kirjaimia käyttämällä murtolukujen kertomissääntö voidaan kirjoittaa seuraavasti:
\(\suuri \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)

Muotoiltua sääntöä käyttämällä voit kertoa murto-osan luonnollisella luvulla, sekamurtoluvulla ja myös kertoa sekamurtoluvut. Tätä varten sinun on kirjoitettava luonnollinen luku murtolukuna, jonka nimittäjä on 1, sekoitettu murtoluku - virheellisenä murtolukuna.

Kertolaskua tulee yksinkertaistaa (jos mahdollista) pienentämällä murto-osaa ja eristämällä väärän jakeen koko osa.

Murtoluvuille, kuten luonnollisille lukuille, pätevät kertolaskujen kommutatiiviset ja kombinatiiviset ominaisuudet sekä kertolaskujen jakautumisominaisuus suhteessa yhteenlaskuun.

Murtolukujen jako

Otetaan murto \(\frac(2)(3)\) ja "käännetään" se vaihtamalla osoittaja ja nimittäjä. Saamme murtoluvun \(\frac(3)(2)\). Tätä murtolukua kutsutaan käänteinen murtoluvut \(\frac(2)(3)\).

Jos nyt "käännämme" murto-osan \(\frac(3)(2)\, saamme alkuperäisen murtoluvun \(\frac(2)(3)\). Siksi murtolukuja, kuten \(\frac(2)(3)\) ja \(\frac(3)(2)\) kutsutaan keskenään käänteisesti.

Esimerkiksi murtoluvut \(\frac(6)(5) \) ja \(\frac(5)(6) \), \(\frac(7)(18) \) ja \(\frac (18) )(7)\).

Kirjaimia käyttämällä käänteismurtoluvut voidaan kirjoittaa seuraavasti: \(\frac(a)(b) \) ja \(\frac(b)(a) \)

On selvää että käänteismurtolukujen tulo on 1. Esimerkki: \(\frac(2)(3) \cdot \frac(3)(2) =1 \)

Käänteismurtolukuja käyttämällä voit vähentää murtolukujen jakamista kertolaskuksi.

Sääntö murtoluvun jakamiseksi murtoluvulla on:
Jos haluat jakaa yhden murtoluvun toisella, sinun on kerrottava osinko jakajan käänteisluvulla.

Kirjaimia käyttämällä murtolukujen jakamissääntö voidaan kirjoittaa seuraavasti:
\(\suuri \frac(a)(b) : \frac(c)(d) = \frac(a)(b) \cdot \frac(d)(c) \)

Jos osinko tai jakaja on luonnollinen luku tai sekamurtoluku, niin murtolukujen jakosäännön käyttämiseksi se on ensin esitettävä virheellisenä murtolukuna.

Murtolukuja käyttämällä koko objektin sama osa voidaan kirjoittaa eri tavoin.

Puolet ympyrästä on varjostettu kuvassa

Joten kaikki nämä murtoluvut ovat yhtä suuria.

Mukavuuden vuoksi lisäkerroin kirjoitetaan murtoluvun yläpuolelle oikealla olevaan vinoviivaan.

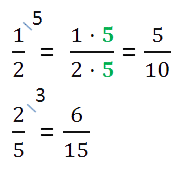
Palataan jälleen murtolukuihimme ja kirjoitetaan ne eri järjestyksessä.

Tiettyä ykköstä vastaava murto-osa voidaan saada, jos murto-osan osoittaja ja nimittäjä jaetaan samanaikaisesti samalla luvulla, joka ei ole nolla.

Tätä murtoluvun muuntamista kutsutaan pienentää murto-osaa.

Murtoluvun pienentäminen kirjoitetaan yleensä seuraavasti.

Osoittaja ja nimittäjä on yliviivattu, ja niiden viereen kirjoitetaan osoittajan ja nimittäjän samalla numerolla jaon tulokset (osamäärät).

Pidä mielessä numero, jolla osoittaja ja nimittäjä jaetaan.

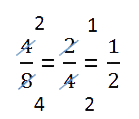
Esimerkissämme pienensimme (eli jakoimme sekä osoittajan että nimittäjän) murto-osan kahdella, minkä pidimme mielessä.

Fraktion pienennys voidaan tehdä peräkkäin.

Murtoluvun pääominaisuus

Muotoilkaamme murtoluvun pääominaisuus.

Jos murtoluvun osoittaja ja nimittäjä kerrotaan tai jaetaan samalla luvulla, joka ei ole nolla, saadaan murto-osa, joka on yhtä suuri kuin annettu.

Kirjoitetaan tämä ominaisuus kirjaimellisten lausekkeiden muodossa.

, jossa "a", "b" ja "k" ovat luonnollisia lukuja.

Murtolukujen pelkistäminen, säännöt ja esimerkkejä murtolukujen vähentämisestä.

Tässä artikkelissa tarkastellaan yksityiskohtaisesti, miten vähentäviä fraktioita. Ensin keskustellaan siitä, mitä kutsutaan murto-osan vähentämiseksi. Tämän jälkeen puhutaan pelkistyvän murto-osan pelkistämisestä pelkistymättömään muotoon. Seuraavaksi hankimme murtolukujen pienentämissäännön ja lopuksi tarkastelemme esimerkkejä tämän säännön soveltamisesta.

Sivulla navigointi.

Mitä murto-osan pienentäminen tarkoittaa?

Tiedämme, että tavalliset jakeet jaetaan pelkistymättömiin ja pelkistymättömiin jakeisiin. Nimien perusteella voi arvata, että pelkistymättömiä murtolukuja voidaan pienentää, mutta pelkistymättömiä ei.

Mitä murto-osan pienentäminen tarkoittaa? Pienennä fraktiota- tämä tarkoittaa, että sen osoittaja ja nimittäjä jaetaan niiden positiivisella ja erolla yksiköstä yhteinen jakaja. On selvää, että murto-osan pienentämisen tuloksena saadaan uusi murto, jolla on pienempi osoittaja ja nimittäjä, ja murto-osan perusominaisuuden vuoksi tuloksena oleva murto-osa on yhtä suuri kuin alkuperäinen.

Pienennetään esimerkiksi yhteistä murtolukua 8/24 jakamalla sen osoittaja ja nimittäjä kahdella. Toisin sanoen vähennetään murto-osaa 8/24 kahdella. Koska 8:2=4 ja 24:2=12, tämä vähennys johtaa murto-osuuteen 4/12, joka on yhtä suuri kuin alkuperäinen murto-osa 8/24 (katso yhtäläiset ja eriarvoiset murtoluvut). Tämän seurauksena meillä on .

Tavallisten jakeiden pelkistäminen pelkistymättömään muotoon

Tyypillisesti murto-osan vähentämisen perimmäinen tavoite on saada pelkistymätön jae, joka on yhtä suuri kuin alkuperäinen pelkistettävä jae. Tämä tavoite voidaan saavuttaa vähentämällä alkuperäistä vähennettävää murtolukua sen osoittajan ja nimittäjän suurimmalla yhteisellä jakajalla. Tällaisen pelkistyksen tuloksena saadaan aina pelkistymätön jae. Todellakin, murto-osa on redusoitumaton, koska GCD:n ominaisuuksista tiedetään, että Ja - molemminpuolisesti alkuluvut. Tässä sanotaan, että murtoluvun osoittajan ja nimittäjän suurin yhteinen jakaja on suurin luku, jolla tätä murtolukua voidaan pienentää.

Niin, yhteisen jakeen pelkistys pelkistymättömään muotoon koostuu alkuperäisen pelkistettävän murtoluvun osoittajan ja nimittäjän jakamisesta niiden gcd:llä.

Katsotaanpa esimerkkiä, jolle palataan murto-osaan 8/24 ja vähennetään sitä lukujen 8 ja 24 suurimmalla yhteisellä jakajalla, joka on yhtä suuri kuin 8. Koska 8:8=1 ja 24:8=3, tulemme redusoitumattomaan murto-osaan 1/3. Joten,.

Huomaa, että ilmaus "vähentää murto-osaa" tarkoittaa usein alkuperäisen jakeen vähentämistä sen pelkistämättömään muotoon. Toisin sanoen murto-osan vähentäminen tarkoittaa hyvin usein osoittajan ja nimittäjän jakamista niiden suurimmalla yhteisellä kertoimella (eikä millään yhteisellä kertoimella).

Kuinka pienentää murto-osaa? Murtolukujen pienentämisen säännöt ja esimerkit

Jäljelle jää vain tarkastella murto-osien pienentämissääntöä, joka selittää kuinka tiettyä murto-osaa pienennetään.

Murtolukujen pienentämisen sääntö koostuu kahdesta vaiheesta:

• ensinnäkin löydetään murtoluvun osoittajan ja nimittäjän gcd;
• toiseksi, murto-osan osoittaja ja nimittäjä jaetaan niiden gcd:llä, mikä antaa redusoitumattoman murtoluvun, joka on yhtä suuri kuin alkuperäinen.

Selvitetään se esimerkki murto-osan pienentämisestä mainitun säännön mukaan.

www.cleverstudents.ru

Murtolukujen vähentäminen. Mitä murto-osan pienentäminen tarkoittaa?

Murtolukujen pienentäminen on tarpeen murtoluvun pelkistämiseksi yksinkertaisempaan muotoon esimerkiksi lausekkeen ratkaisemisen tuloksena saadussa vastauksessa.

Murtolukujen pienentäminen, määritelmä ja kaava.

Mitä fraktioiden vähentäminen tarkoittaa? Mitä murto-osan pienentäminen tarkoittaa?

Määritelmä:
Murtolukujen vähentäminen- tämä on murtoluvun osoittajan ja nimittäjän jako samalla positiivisella luvulla, joka ei ole nolla ja yksi. Pelkistyksen tuloksena saadaan murto, jolla on pienempi osoittaja ja nimittäjä, joka on yhtä suuri kuin edellinen murto pääominaisuuden mukaan rationaalisia lukuja.

Kaava fraktioiden vähentämiseksi rationaalilukujen perusominaisuudet.

Katsotaanpa esimerkkiä:
Pienennä murtolukua \(\frac \)

Ratkaisu:
Voimme laskea murto-osan alkutekijöiksi ja kumota yhteiset tekijät.

Vastaus: vähentämisen jälkeen saimme murto-osan \(\frac\). Rationaalilukujen perusominaisuuden mukaan alkuperäinen ja tuloksena oleva murtoluku ovat yhtä suuret.

Kuinka vähentää fraktioita? Murto-osan pelkistäminen redusoitumattomaan muotoonsa.

Jotta tuloksena saadaan pelkistymätön murto-osa, tarvitsemme löytää suurin yhteinen jakaja (GCD) murtoluvun osoittajalle ja nimittäjälle.

GCD:n löytämiseen on useita tapoja; esimerkissä käytämme lukujen hajottamista alkutekijöiksi.

Hanki redusoitumaton murtoluku \(\frac\).

Ratkaisu:
Etsitään GCD(48, 136). Kirjoitetaan luvut 48 ja 136 alkutekijöiksi.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
GCD(48; 136) = 2⋅2⋅2 = 6

Sääntö murto-osan pelkistämiseksi pelkistymättömään muotoon.

1. Sinun on löydettävä osoittajalle ja nimittäjälle suurin yhteinen jakaja.
2. Sinun on jaettava osoittaja ja nimittäjä suurimmalla yhteisellä jakajalla saadaksesi jaon tuloksena redusoitumattoman murtoluvun.

Esimerkki:
Pienennä murtolukua \(\frac\).

Ratkaisu:
Etsitään GCD(152, 168). Kirjoitetaan luvut 152 ja 168 alkutekijöiksi.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
GCD(152; 168) = 2⋅2⋅2 = 6

Vastaus: \(\frac \) on pelkistymätön murtoluku.

Väärien murtolukujen vähentäminen.

Kuinka lyhentää oikea murto-osa?
Murto-osien pienentämissäännöt ovat samat oikeille ja väärille jakeille.

Katsotaanpa esimerkkiä:
Pienennä väärää murtolukua \(\frac\).

Ratkaisu:
Kirjoitetaan osoittaja ja nimittäjä yksinkertaisiksi tekijöiksi. Ja sitten vähennämme yhteisiä tekijöitä.

Sekafraktioiden vähentäminen.

Sekajakeet noudattavat samoja sääntöjä kuin tavalliset jakeet. Ainoa ero on, että voimme älä kosketa koko osaa, vaan pienennä murto-osaa tai Muunna sekafraktio vääräksi jakeeksi, vähennä sitä ja muunna se takaisin oikeaksi jakeeksi.

Katsotaanpa esimerkkiä:
Peruuta sekoitettu murtoluku \(2\frac\).

Ratkaisu:
Ratkaistaan ​​se kahdella tavalla:
Ensimmäinen tapa:
Kirjoitetaan murto-osa yksinkertaisiksi tekijöiksi, mutta emme kosketa koko osaa.

Toinen tapa:
Muunnetaan se ensin vääräksi murtoluvuksi ja kirjoitetaan sitten alkutekijöiksi ja vähennetään. Muunnetaan tuloksena oleva virheellinen murto oikeaksi murtoluvuksi.

Aiheeseen liittyviä kysymyksiä:
Voitko pienentää murtolukuja, kun lisäät tai vähennät?
Vastaus: ei, sinun on ensin lisättävä tai vähennettävä murtolukuja sääntöjen mukaisesti ja vasta sitten vähennettävä niitä. Katsotaanpa esimerkkiä:

Ratkaisu:
He tekevät usein sen virheen, että vähentävät samoja numeroita osoittajassa ja nimittäjässä, meidän tapauksessamme lukua 20, mutta niitä ei voida pienentää ennen kuin olet suorittanut yhteen- ja vähennyslaskun.

Millä luvuilla voit pienentää murto-osan?
Vastaus: Voit pienentää murto-osaa suurimmalla yhteisellä kertoimella tai osoittajan ja nimittäjän yhteisellä jakajalla. Esimerkiksi murto-osa \(\frac \).

Kirjoitetaan luvut 100 ja 150 alkutekijöiksi.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Suurin yhteinen jakaja on luku gcd(100, 150)= 2⋅5⋅5=50

Saimme redusoitumattoman murto-osan \(\frac \).

Mutta aina ei tarvitse jakaa gcd:llä; pelkistämätöntä murtolukua ei aina tarvita; murto-osaa voi pienentää osoittajan ja nimittäjän yksinkertaisella jakajalla. Esimerkiksi luvuilla 100 ja 150 on yhteinen jakaja 2. Pienennetään murtolukua \(\frac \) kahdella.

Saimme pienennettävän murto-osan \(\frac\).

Mitä fraktioita voidaan vähentää?
Vastaus: Voit pienentää murtolukuja, joissa osoittajalla ja nimittäjällä on yhteinen jakaja. Esimerkiksi murto-osa \(\frac \). Lukuilla 4 ja 8 on luku, jolla ne molemmat ovat jaollisia - luku 2. Siksi tällainen murto-osa voidaan vähentää luvulla 2.

Esimerkki:
Vertaa kahta murtolukua \(\frac \) ja \(\frac \).

Nämä kaksi murto-osaa ovat yhtä suuret. Katsotaanpa tarkemmin murto-osaa \(\frac \):

Kaksi murto-osaa ovat yhtä suuret, jos ja vain, jos toinen niistä saadaan vähentämällä toinen murto-osa osoittajan ja nimittäjän yhteisellä kertoimella.

Esimerkki:
Pienennä seuraavia murtolukuja, jos mahdollista: a) \(\frac \) b) \(\frac \) c) \(\frac \) d) \(\frac \)

Operaatiot tavallisilla murtoluvuilla

Fraktion laajennus. Murto-osan pienentäminen. Murtolukujen vertailu.

Vähentäminen yhteiseksi nimittäjäksi. Yhteen-ja vähennyslasku murto-osia

Murtolukujen kertominen. Murtolukujen jako .

Fraktion laajennus. Murtoluvun arvo ei muutu, jos sen osoittaja ja nimittäjä kerrotaan samalla luvulla kuin nollalla. murto-osan laajennus. Esimerkiksi,



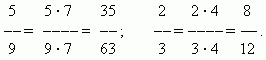
Murto-osan pienentäminen. Murtoluvun arvo ei muutu, jos jaat sen osoittajan ja nimittäjän samalla luvulla kuin nollalla.. Tätä muutosta kutsutaan pienentää murto-osaa. Esimerkiksi,



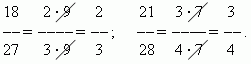
Murtolukujen vertailu. Kahdesta murtoluvusta, joilla on samat osoittajat, se, jonka nimittäjä on pienempi, on suurempi:



Kahdesta murtoluvusta, joilla on sama nimittäjä, se, jonka osoittaja on suurempi, on suurempi:



Jos haluat verrata murtolukuja, joilla on eri osoittajat ja nimittäjät, sinun on laajennettava niitä, jotta ne saadaan yhteiseksi nimittäjäksi.

ESIMERKKI Vertaa kahta murtolukua:

Laajennetaan ensimmäistä murtolukua toisen nimittäjällä ja toista ensimmäisen nimittäjällä:

Tässä käytetty muunnos on ns murto-osien vähentäminen yhteiseksi nimittäjäksi.

Murtolukujen lisääminen ja vähentäminen. Jos murtolukujen nimittäjät ovat samat, murtolukujen lisäämiseksi sinun on lisättävä niiden osoittajat, ja murtolukujen vähentämiseksi sinun on vähennettävä niiden osoittajat (samassa järjestyksessä). Tuloksena oleva summa tai erotus on tuloksen osoittaja; nimittäjä pysyy samana. Jos murto-osien nimittäjät ovat erilaiset, sinun on ensin vähennettävä murtoluvut yhteiseksi nimittäjäksi. Kun lisätään sekalukuja, niiden kokonais- ja murto-osat lisätään erikseen. Kun vähennät sekalukuja, suosittelemme muuntamaan ne ensin virheellisiksi murtoluvuiksi, sitten vähentämään toisiaan ja muuttamaan tuloksen tarvittaessa uudelleen sekalukumuotoon.



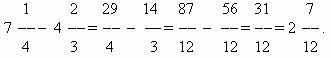
Murtolukujen kertominen. Luvun kertominen murtoluvulla tarkoittaa sen kertomista osoittajalla ja tulon jakamista nimittäjällä. Siksi meillä on yleissääntö murtolukujen kertominen: jos haluat kertoa murtoluvut, sinun on kerrottava niiden osoittajat ja nimittäjät erikseen ja jaettava ensimmäinen tulo toisella.

ESIMERKKI

Murtolukujen jakaminen. Jos haluat jakaa luvun murtoluvulla, sinun on kerrottava tämä luku käänteismurtoluvulla. Tämä sääntö seuraa jaon määritelmästä (katso kohta "Aritmeettiset operaatiot").

ESIMERKKI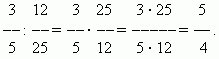

Murtolukujen kertominen ja jako

Viime kerralla opimme lisäämään ja vähentämään murtolukuja (katso oppitunti "Murtolukujen lisääminen ja vähentäminen"). Vaikein osa noista toimista oli murto-osien tuominen yhteiselle nimittäjälle.

Nyt on aika käsitellä kerto- ja jakolaskua. Hyviä uutisia on, että nämä operaatiot ovat jopa yksinkertaisempia kuin yhteen- ja vähennyslasku. Tarkastellaan ensin yksinkertaisinta tapausta, jossa on kaksi positiivista murtolukua ilman erotettua kokonaislukuosaa.

Jos haluat kertoa kaksi murtolukua, sinun on kerrottava niiden osoittajat ja nimittäjät erikseen. Ensimmäinen numero on uuden murtoluvun osoittaja ja toinen on nimittäjä.

Kahden murto-osan jakamiseksi sinun on kerrottava ensimmäinen murto-osa "käänteisellä" toisella murto-luvulla.

Määritelmästä seuraa, että murtolukujen jakaminen pelkistyy kertolaskuksi. Jos haluat "kääntää" murto-osan, vaihda osoittaja ja nimittäjä. Siksi koko oppitunnin ajan käsittelemme pääasiassa kertolaskua.

Kertomisen seurauksena voi syntyä (ja usein syntyy) pienennettävä murto-osa - sitä on tietysti vähennettävä. Jos kaikkien vähennysten jälkeen murto-osa osoittautuu vääräksi, koko osa tulee korostaa. Mutta mitä ei varmasti tapahdu kertolaskussa, on pelkistys yhteiseen nimittäjään: ei ristikkäisiä menetelmiä, suurimmat tekijät ja vähiten yhteiset kerrannaiset.



Murtolukujen kertominen kokonaisilla osilla ja negatiivisilla murtoluvuilla

Jos murtoluvut sisältävät kokonaislukuosan, ne on muutettava virheellisiksi - ja vasta sitten kerrottava edellä esitettyjen kaavioiden mukaisesti.

Jos murtoluvun osoittajassa, nimittäjässä tai sen edessä on miinus, se voidaan ottaa pois kertolaskusta tai poistaa kokonaan seuraavien sääntöjen mukaisesti:

1. Plus miinuksella antaa miinuksen;
2. Kaksi negatiivista tekee myöntävän.

Tähän asti näitä sääntöjä on kohdattu vain negatiivisia murtolukuja lisättäessä ja vähennettäessä, kun koko osasta oli päästävä eroon. Teoksen osalta ne voidaan yleistää useiden haittojen "polttamiseksi" kerralla:

3. Yliviivaamme negatiivit pareittain, kunnes ne katoavat kokonaan. Äärimmäisissä tapauksissa yksi miinus voi selviytyä - se, jolle ei ollut kumppania;
4. Jos miinuksia ei ole jäljellä, toimenpide on valmis - voit aloittaa kertomisen. Jos viimeistä miinusta ei ole yliviivattu, koska sillä ei ollut paria, jätämme sen kertolaskurajojen ulkopuolelle. Tuloksena on negatiivinen murto-osa.

Tehtävä. Etsi ilmaisun merkitys:

Muunnamme kaikki murtoluvut vääriksi ja poistamme kertolaskusta miinukset. Kerromme sen, mikä on jäljellä tavallisten sääntöjen mukaisesti. Saamme:



Muistutan vielä kerran, että miinus, joka näkyy korostetun kokonaisosan murto-osan edessä, viittaa nimenomaan koko murto-osaan, ei vain sen kokonaisuuteen (tämä koskee kahta viimeistä esimerkkiä).

Huomaa myös negatiivisia lukuja: Kun kerrotaan, ne on suljettu suluissa. Tämä tehdään miinusten erottamiseksi kertomerkeistä ja koko merkinnän tarkentamiseksi.

Murtolukujen vähentäminen lennossa

Kertominen on erittäin työvoimavaltainen toimenpide. Tässä olevat luvut osoittautuvat melko suuriksi, ja ongelman yksinkertaistamiseksi voit yrittää pienentää murto-osaa edelleen ennen kertolaskua. Todellakin, pohjimmiltaan murtolukujen osoittajat ja nimittäjät ovat tavallisia tekijöitä, ja siksi niitä voidaan pienentää murtoluvun perusominaisuutta käyttämällä. Katso esimerkkejä:



Määritelmän mukaan meillä on:



Kaikissa esimerkeissä vähennetyt numerot ja niistä jääneet on merkitty punaisella.

Huomaa: ensimmäisessä tapauksessa kertoimia pienennettiin kokonaan. Niiden tilalle jää yksiköitä, joita ei yleisesti ottaen tarvitse kirjoittaa. Toisessa esimerkissä ei ollut mahdollista saavuttaa täydellistä vähennystä, mutta laskelmien kokonaismäärä kuitenkin pieneni.

Älä kuitenkaan koskaan käytä tätä tekniikkaa, kun lisäät ja vähennät murtolukuja! Kyllä, joskus on samanlaisia ​​lukuja, joita haluat vain vähentää. Tässä, katso:

Et voi tehdä sitä!

Virhe johtuu siitä, että kun lasketaan yhteen, murtoluvun osoittaja tuottaa summan, ei lukujen tuloa. Näin ollen on mahdotonta soveltaa murtoluvun perusominaisuutta, koska tämä ominaisuus koskee nimenomaan lukujen kertomista.

Murtolukujen vähentämiseen ei yksinkertaisesti ole muita syitä, joten oikea ratkaisu edelliseen ongelmaan näyttää tältä:

Kuten näette, oikea vastaus ei osoittautunut niin kauniiksi. Yleisesti ottaen ole varovainen.

Tämä artikkeli jatkaa algebrallisten murtolukujen muuntamisen aihetta: harkitse sellaista toimintaa algebrallisten murtolukujen vähentämiseksi. Määritellään itse termi, muotoillaan pelkistyssääntö ja analysoidaan käytännön esimerkkejä.

Yandex.RTB R-A-339285-1

Algebrallisen murtoluvun pienentämisen merkitys

Yleisiä jakeita koskevissa materiaaleissa tarkastelimme sen vähentämistä. Määritimme murtoluvun vähentämisen jakamalla sen osoittaja ja nimittäjä yhteisellä kertoimella.

Algebrallisen murtoluvun pienentäminen on samanlainen operaatio.

Määritelmä 1

Algebrallisen murtoluvun pienentäminen on sen osoittajan ja nimittäjän jako yhteisellä kertoimella. Tässä tapauksessa, toisin kuin tavallisen murto-osan pelkistäminen (yhteinen nimittäjä voi olla vain luku), algebrallisen murtoluvun osoittajan ja nimittäjän yhteinen tekijä voi olla polynomi, erityisesti monomi tai luku.

Esimerkiksi algebrallinen murtoluku 3 x 2 + 6 x y 6 x 3 y + 12 x 2 y 2 voidaan vähentää numerolla 3, jolloin tuloksena on: x 2 + 2 x y 6 x 3 · y + 12 · x 2 · y 2. Voimme pienentää saman murto-osan muuttujalla x, jolloin saadaan lauseke 3 x + 6 y 6 x 2 y + 12 x y 2. On myös mahdollista pienentää annettua murto-osaa monomilla 3 x tai jokin polynomeista x + 2 v, 3 x + 6 y , x 2 + 2 x y tai 3 x 2 + 6 x v.

Algebrallisen murtoluvun pienentämisen perimmäinen tavoite on yksinkertaisemman muodon murto-osa, parhaimmillaan pelkistymätön murto-osa.

Ovatko kaikki algebralliset murtoluvut pelkistyksen kohteena?

Jälleen, tavallisissa jakeissa olevista materiaaleista tiedämme, että on olemassa pelkistyviä ja pelkistymättömiä jakeita. Pelkistymättömät murtoluvut ovat murtolukuja, joilla ei ole muita yhteisiä osoittaja- ja nimittäjätekijöitä kuin 1.

Sama koskee algebrallisia murtolukuja: niillä voi olla yhteisiä kertoimia osoittajassa ja nimittäjässä tai ei. Yhteisten tekijöiden läsnäolon avulla voit yksinkertaistaa alkuperäistä murto-osaa vähentämällä. Kun yhteisiä tekijöitä ei ole, on mahdotonta optimoida tiettyä murto-osaa pelkistysmenetelmällä.

Yleisissä tapauksissa murto-osan tyyppi huomioon ottaen on melko vaikea ymmärtää, voidaanko sitä pienentää. Tietysti joissakin tapauksissa osoittajan ja nimittäjän välinen yhteinen tekijä on ilmeinen. Esimerkiksi algebrallisessa murtoluvussa 3 x 2 3 y on aivan selvää, että yhteinen tekijä on luku 3.

Murtoluvussa - x · y 5 · x · y · z 3 ymmärrämme myös heti, että sitä voidaan pienentää x:llä, y:llä tai x · y:lla. Ja silti, paljon useammin on esimerkkejä algebrallisista murtoluvuista, kun osoittajan ja nimittäjän yhteinen tekijä ei ole niin helppo nähdä, ja vielä useammin se yksinkertaisesti puuttuu.

Voimme esimerkiksi pienentää murtolukua x 3 - 1 x 2 - 1 x - 1:llä, kun määritettyä yhteistä tekijää ei ole merkinnässä. Mutta murto-osaa x 3 - x 2 + x - 1 x 3 + x 2 + 4 · x + 4 ei voi pienentää, koska osoittajalla ja nimittäjällä ei ole yhteistä tekijää.

Näin ollen kysymys algebrallisen murtoluvun pelkistävyyden määrittämisestä ei ole niin yksinkertainen, ja usein on helpompi työskennellä tietyn muodon murto-osan kanssa kuin yrittää selvittää, onko se pelkistävissä. Tällöin tapahtuu sellaisia ​​muunnoksia, jotka tietyissä tapauksissa mahdollistavat osoittajan ja nimittäjän yhteisen tekijän määrittämisen tai johtopäätöksen murto-osan redusoitumattomuudesta. Tutkimme tätä asiaa yksityiskohtaisesti artikkelin seuraavassa kappaleessa.

Algebrallisten murtolukujen pienentämissääntö

Algebrallisten murtolukujen pienentämissääntö koostuu kahdesta peräkkäisestä toimenpiteestä:

• osoittajan ja nimittäjän yhteisten tekijöiden löytäminen;
• jos niitä löytyy, fraktion vähentämistoimenpide suoritetaan suoraan.

Kätevin tapa löytää yhteisiä nimittäjiä on kertoa tietyn algebrallisen murtoluvun osoittajassa ja nimittäjässä olevat polynomit. Tämän avulla voit välittömästi nähdä selkeästi yleisten tekijöiden olemassaolon tai puuttumisen.

Itse algebrallisen murtoluvun pelkistystoiminto perustuu algebrallisen murtoluvun pääominaisuuteen, joka ilmaistaan ​​yhtälöllä määrittelemätön, jossa a, b, c ovat joitakin polynomeja ja b ja c ovat nollia poikkeavia. Ensimmäinen askel on pelkistää murto muotoon a · c b · c, jossa huomaamme välittömästi yhteisen tekijän c. Toinen vaihe on tehdä vähennys, ts. siirtyminen muodon a b murto-osaan.

Tyypillisiä esimerkkejä

Ilmeisyydestä huolimatta selvennetään asiaa erikoistapaus kun algebrallisen murtoluvun osoittaja ja nimittäjä ovat yhtä suuret. Samanlaiset murtoluvut ovat identtisesti yhtä suuria kuin 1 tämän murtoluvun muuttujien koko ODZ:ssä:

5 5 = 1; - 2 3 - 2 3 = 1; x x = 1; - 3, 2 x 3 - 3, 2 x 3 = 1; 1 2 · x - x 2 · y 1 2 · x - x 2 · y;

Koska tavalliset murtoluvut ovat algebrallisten murtolukujen erikoistapaus, muistetaan kuinka ne pelkistetään. Osoittajaan ja nimittäjään kirjoitetut luonnolliset luvut lasketaan alkutekijöiksi, jolloin yhteiset tekijät kumotaan (jos niitä on).

Esimerkiksi 24 1260 = 2 2 2 3 2 2 3 3 5 7 = 2 3 5 7 = 2 105

Yksinkertaisten identtisten kertoimien tulo voidaan kirjoittaa potenssiksi, ja murto-osan pienentämisessä käyttää ominaisuutta jakaa potenssit identtisillä emäksillä. Sitten yllä oleva ratkaisu olisi:

24 1260 = 2 3 3 2 2 3 2 5 7 = 2 3 - 2 3 2 - 1 5 7 = 2 105

(osoittaja ja nimittäjä jaettuna yhteisellä kertoimella 2 2 3). Tai selvyyden vuoksi, kerto- ja jakolaskuominaisuuksien perusteella, annamme ratkaisulle seuraavan muodon:

24 1260 = 2 3 3 2 2 3 2 5 7 = 2 3 2 2 3 3 2 1 5 7 = 2 1 1 3 1 35 = 2 105

Analogisesti suoritetaan algebrallisten murtolukujen pelkistys, jossa osoittajalla ja nimittäjällä on monomiaalit kokonaislukukertoimilla.

Esimerkki 1

Algebrallinen murtoluku on annettu - 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z. Sitä on vähennettävä.

Ratkaisu

On mahdollista kirjoittaa tietyn murtoluvun osoittaja ja nimittäjä yksinkertaisten tekijöiden ja muuttujien tulona ja sitten suorittaa pelkistys:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = -3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · z = = - 3 · 3 · a · a · a 2 · c · c · c · c · c · c = - 9 a 3 2 c 6

Kuitenkin järkevämpi tapa olisi kirjoittaa ratkaisu lausekkeeksi, jolla on potenssit:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = - 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = - 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = - 3 3 - 1 2 · a 5 - 2 1 · 1 · 1 c 7 - 1 · 1 = · - 3 2 · a 3 2 · c 6 = · - 9 · a 3 2 · c 6 .

Vastaus:- 27 a 5 b 2 c z 6 a 2 b 2 c 7 z = - 9 a 3 2 c 6

Kun algebrallisen murtoluvun osoittaja ja nimittäjä sisältävät murto-lukukertoimia, on kaksi mahdollista jatkotoimia: joko jakaa nämä murtokertoimet erikseen tai ensin päästään eroon murto-osista kertomalla osoittaja ja nimittäjä jollain luonnollisella luvulla. Viimeinen muunnos suoritetaan algebrallisen murto-osan perusominaisuuden vuoksi (voit lukea siitä artikkelista "Algebrallisen murtoluvun pienentäminen uuteen nimittäjään").

Esimerkki 2

Annettu murtoluku on 2 5 x 0, 3 x 3. Sitä on vähennettävä.

Ratkaisu

On mahdollista pienentää murto-osaa seuraavasti:

2 5 x 0, 3 x 3 = 2 5 3 10 x x 3 = 4 3 1 x 2 = 4 3 x 2

Yritetään ratkaista ongelma eri tavalla, päästyämme ensin eroon murtokertoimista - kerrotaan osoittaja ja nimittäjä näiden kertoimien nimittäjien pienimmällä yhteisellä kerrannaisuudella, ts. LCM:ssä (5, 10) = 10. Sitten saamme:

2 5 x 0, 3 x 3 = 10 2 5 x 10 0, 3 x 3 = 4 x 3 x 3 = 4 3 x 2.

Vastaus: 2 5 x 0, 3 x 3 = 4 3 x 2

Kun vähennämme algebrallisia murtolukuja yleisnäkymä, jossa osoittajat ja nimittäjät voivat olla joko monomeja tai polynomeja, voi olla ongelma, kun yhteinen tekijä ei aina ole heti näkyvissä. Tai sitä paitsi sitä ei yksinkertaisesti ole olemassa. Sitten yhteisen tekijän määrittämiseksi tai sen puuttumisen kirjaamiseksi otetaan huomioon algebrallisen murtoluvun osoittaja ja nimittäjä.

Esimerkki 3

Rationaalinen murtoluku 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 - 49 · b 3 on annettu. Sitä on vähennettävä.

Ratkaisu

Otetaan huomioon polynomit osoittajassa ja nimittäjässä. Laitetaan se pois suluista:

2 a 2 b 2 + 28 a b 2 + 98 b 2 a 2 b 3 - 49 b 3 = 2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49)

Näemme, että suluissa oleva lauseke voidaan muuntaa käyttämällä lyhennettyjä kertolaskukaavoja:

2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49) = 2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7)

On selvästi nähtävissä, että murto-osaa on mahdollista pienentää yhteisellä kertoimella b 2 (a + 7). Tehdään vähennys:

2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7) = 2 (a + 7) b (a - 7) = 2 a + 14 a b - 7 b

Kirjoitetaan lyhyt ratkaisu ilman selitystä yhtäläisyyksien ketjuna:

2 a 2 b 2 + 28 a b 2 + 98 b 2 a 2 b 3 - 49 b 3 = 2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49) = = 2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7) = 2 (a + 7) b (a - 7) = 2 a + 14 a b - 7 b

Vastaus: 2 a 2 b 2 + 28 a b 2 + 98 b 2 a 2 b 3 - 49 b 3 = 2 a + 14 a b - 7 b.

Tapahtuu, että yhteiset tekijät piilotetaan numeeristen kertoimien avulla. Sitten murtolukuja pienennettäessä on optimaalista laittaa numeeriset tekijät osoittajan ja nimittäjän korkeammilla potenssilla suluista pois.

Esimerkki 4

Algebrallinen murtoluku 1 5 · x - 2 7 · x 3 · y 5 · x 2 · y - 3 1 2 . Sitä on tarpeen vähentää, jos mahdollista.

Ratkaisu

Ensi silmäyksellä osoittajalla ja nimittäjällä ei ole yhteistä nimittäjää. Yritetään kuitenkin muuntaa annettu murto-osa. Otetaan kertoimesta x pois:

1 5 x - 2 7 x 3 v 5 x 2 v - 3 1 2 = x 1 5 - 2 7 x 2 v 5 x 2 v - 3 1 2

Nyt voit nähdä jonkin verran samankaltaisuutta suluissa olevan lausekkeen ja nimittäjässä olevan lausekkeen välillä x 2 y:n takia . Otetaan näiden polynomien suurempien potenssien numeeriset kertoimet:

x 1 5 - 2 7 x 2 y 5 x 2 y - 3 1 2 = x - 2 7 - 7 2 1 5 + x 2 y 5 x 2 v - 1 5 3 1 2 = = - 2 7 x - 7 10 + x 2 v 5 x 2 v - 7 10

Nyt yhteinen tekijä tulee näkyviin, suoritamme vähennyksen:

2 7 x - 7 10 + x 2 v 5 x 2 v - 7 10 = - 2 7 x 5 = - 2 35 x

Vastaus: 1 5 x - 2 7 x 3 y 5 x 2 y - 3 1 2 = - 2 35 x .

Korostakaamme, että taitoa supistuminen rationaaliset murtoluvut riippuu kyvystä kertoa polynomit.

Jos huomaat tekstissä virheen, korosta se ja paina Ctrl+Enter

Online-laskin suorittaa algebrallisten murtolukujen vähentäminen murto-osien pelkistyssäännön mukaisesti: korvataan alkuperäinen murto yhtä suurella murtoluvulla, mutta pienemmällä osoittajalla ja nimittäjällä, ts. Murtoluvun osoittaja ja nimittäjä jaetaan samanaikaisesti niiden yhteisellä suurimmalla yhteisellä kertoimella (GCD). Laskin näyttää myös yksityiskohtaisen ratkaisun, joka auttaa sinua ymmärtämään vähennysjärjestyksen.

Annettu:

Ratkaisu:

Suoritetaan murtolukuvähennystä

tarkastetaan mahdollisuus suorittaa algebrallinen murtolukuvähennys

1) Murtoluvun osoittajan ja nimittäjän suurimman yhteisen jakajan (GCD) määrittäminen

määritetään algebrallisen murtoluvun osoittajan ja nimittäjän suurin yhteinen jakaja (GCD)

2) Murtoluvun osoittajan ja nimittäjän pienentäminen

algebrallisen murtoluvun osoittajan ja nimittäjän vähentäminen

3) Murto-osan koko osan valinta

erottamalla algebrallisen murtoluvun koko osa

4) Algebrallisen murtoluvun muuntaminen desimaalimurtoluvuksi

muunnetaan algebrallinen murto desimaali

Apua projektin verkkosivujen kehittämiseen

Hyvä sivuston vierailija.
Jos et löytänyt etsimääsi, muista kirjoittaa siitä kommentteihin, mitä sivustolta tällä hetkellä puuttuu. Tämä auttaa meitä ymmärtämään, mihin suuntaan meidän on edettävä, ja muut kävijät voivat pian saada tarvittavan materiaalin.
Jos sivusto osoittautui sinulle hyödylliseksi, lahjoita sivusto projektille vain 2 ₽ ja tiedämme, että olemme menossa oikeaan suuntaan.

Kiitos kun poikkesit!

I. Menettely algebrallisen murtoluvun pienentämiseksi online-laskimella:

1. Algebrallisen murtoluvun pienentämiseksi syötä murto-osan osoittajan ja nimittäjän arvot asianmukaisiin kenttiin. Jos murto on sekoitettu, täytä myös koko murto-osaa vastaava kenttä. Jos murto-osa on yksinkertainen, jätä koko osakenttä tyhjäksi.
2. Jos haluat määrittää negatiivisen murtoluvun, aseta miinusmerkki murtoluvun koko osaan.
3. Määritetystä algebrallisesta murtoluvusta riippuen suoritetaan automaattisesti seuraava toimintosarja:

• murtoluvun osoittajan ja nimittäjän suurimman yhteisen jakajan (GCD) määrittäminen;
• murtoluvun osoittaja ja nimittäjä vähennetään gcd:llä;
• korostaen murto-osan koko osan, jos viimeisen murtoluvun osoittaja on suurempi kuin nimittäjä.
• muuntaa lopullinen algebrallinen murto desimaalimurtoluvuksi pyöristetty lähimpään sadasosaan.

II. Viitteeksi:

Murtoluku on luku, joka koostuu yksikön yhdestä tai useammasta osasta (murto-osasta). Murtoluku(yksinkertainen murtoluku) kirjoitetaan kahdella numerolla (murto-osuuden osoittaja ja murto-osan nimittäjä), jotka on erotettu toisistaan ​​vaakasuoralla pylvällä (murtoluku), joka osoittaa jakomerkkiä. Murtoluvun osoittaja on murtoviivan yläpuolella oleva luku. Osoittaja näyttää kuinka monta osaketta kokonaisuudesta otettiin. Murtoluvun nimittäjä on murtoviivan alapuolella oleva luku. Nimittäjä näyttää kuinka moneen yhtä suureen osaan kokonaisuus on jaettu. Yksinkertainen murto-osa on murto-osa, jolla ei ole kokonaista osaa. Yksinkertainen murtoluku voi olla oikea tai väärä. Oikea murtoluku on murtoluku, jonka osoittaja on pienempi kuin sen nimittäjä, joten oikea murtoluku on aina pienempi kuin yksi. Esimerkki oikeista murtoluvuista: 8/7, 11/19, 16/17. Virheellinen murtoluku on murtoluku, jonka osoittaja on suurempi tai yhtä suuri kuin nimittäjä, joten väärä murtoluku on aina suurempi tai yhtä suuri kuin yksi. Esimerkki virheellisistä murtoluvuista: 7/6, 8/7, 13/13. sekamurtoluku on luku, joka sisältää kokonaisluvun ja oikean murtoluvun ja ilmaisee tämän kokonaisluvun ja oikean murtoluvun summaa. Mikä tahansa sekafraktio voidaan muuntaa vääräksi jakeeksi yksinkertainen murto-osa. Esimerkki sekafraktioista: 1¼, 2½, 4¾.

III. Huomautus:

1. Lähdetietolohko on korostettu keltaisella, välilaskentalohko varattu sininen , ratkaisulohko on korostettu vihreällä.
2. Voit lisätä, vähentää, kertoa ja jakaa tavallisia tai sekamurtolukuja käyttämällä online-murtolaskuria yksityiskohtainen ratkaisu.

Tiedämme siis jo, että murto-osan osoittaja ja nimittäjä voidaan kertoa ja jakaa samalla luvulla, murto-osa ei muutu. Harkitse kolmea lähestymistapaa:

Lähesty yhtä.

Pienentääksesi jakamalla osoittaja ja nimittäjä yhteisellä jakajalla. Katsotaanpa esimerkkejä:

Lyhennetään:

Annetuissa esimerkeissä näemme heti, mitkä jakajat otetaan pelkistykseen. Prosessi on yksinkertainen - käymme läpi 2,3,4,5 ja niin edelleen. Useimmissa koulukurssiesimerkeissä tämä riittää. Mutta jos se on murto-osa:

Tässä jakajien valintaprosessi voi kestää kauan;). Tietenkin tällaiset esimerkit ovat koulun opetussuunnitelman ulkopuolella, mutta sinun on kyettävä selviytymään niistä. Alla tarkastellaan, kuinka tämä tehdään. Palataan toistaiseksi supistusprosessiin.

Kuten edellä mainittiin, murto-osan pienentämiseksi jaoimme määrittämillämme yhteisillä jakajilla. Kaikki on oikein! Sinun tarvitsee vain lisätä numeroiden jaollisuuden merkkejä:

- jos luku on parillinen, se on jaollinen kahdella.

- jos luku kahdesta viimeisestä numerosta on jaollinen 4:llä, itse luku on jaollinen 4:llä.

— jos luvun muodostavien numeroiden summa on jaollinen kolmella, niin itse luku on jaollinen kolmella. Esimerkiksi 125031, 1+2+5+0+3+1=12. Kaksitoista on jaollinen kolmella, joten 123031 on jaollinen kolmella.

- jos luku päättyy 5:een tai 0:aan, niin luku on jaollinen 5:llä.

— jos luvun muodostavien numeroiden summa on jaollinen 9:llä, niin luku itse on jaollinen 9:llä. Esimerkiksi 625032 =.> 6+2+5+0+3+2=18. Kahdeksantoista on jaollinen 9:llä, mikä tarkoittaa, että 623032 on jaollinen 9:llä.

Toinen lähestymistapa.

Lyhyesti sanottuna itse asiassa koko toiminta tiivistyy osoittajan ja nimittäjän laskemiseen ja sitten yhtäläisten kertoimien vähentämiseen osoittajassa ja nimittäjässä (tämä lähestymistapa on seurausta ensimmäisestä lähestymistavasta):

Visuaalisesti, sekaannusten ja virheiden välttämiseksi, samat tekijät on yksinkertaisesti yliviivattu. Kysymys - kuinka laskea luku? Kaikki jakajat on määritettävä etsimällä. Tämä on erillinen aihe, se ei ole monimutkaista, etsi tietoa oppikirjasta tai Internetistä. Et kohtaa suuria ongelmia factoring-lukujen kanssa, jotka ovat läsnä koulun murtoluvuissa.

Muodollisesti vähennysperiaate voidaan kirjoittaa seuraavasti:

Lähesty kolme.

Tässä on mielenkiintoisin asia edistyneille ja sellaisiksi haluaville. Vähennetään murto-osaa 143/273. Kokeile itse! No, miten se tapahtui nopeasti? Katso nyt!

Käännämme sen (vaihdamme osoittajan ja nimittäjän paikkoja). Jaamme tuloksena olevan murto-osan kulmalla ja muunnamme sen sekaluvuksi, eli valitsemme koko osan:

Se on jo helpompaa. Näemme, että osoittaja ja nimittäjä voidaan pienentää 13:lla:

Älä nyt unohda kääntää murto-osaa takaisin, kirjoitetaan koko ketju ylös:

Tarkastettu - se vie vähemmän aikaa kuin jakajien etsiminen ja tarkistaminen. Palataan kahteen esimerkkiimme:

Ensimmäinen. Jakamalla kulmalla (ei laskimella), saamme:

Tämä murto-osa on tietysti yksinkertaisempi, mutta vähentäminen on jälleen ongelma. Nyt analysoimme erikseen murto-osan 1273/1463 ja käännämme sen:

Täällä on helpompaa. Voimme harkita jakajaa, kuten 19. Muut eivät sovellu, tämä on selvää: 190:19 = 10, 1273:19 = 67. Hurraa! kirjoitetaan:

Seuraava esimerkki. Lyhennetään 88179/2717.

Jaa, saamme:

Analysoimme erikseen murto-osan 1235/2717 ja käännämme sen:

Voimme harkita jakajaa, kuten 13 (enintään 13 ei sovellu):

Osoittaja 247:13=19 Nimittäjä 1235:13=95

*Prosessin aikana näimme toisen jakajan, joka on yhtä suuri kuin 19. Osoittautuu, että:

Nyt kirjoitamme muistiin alkuperäisen numeron:

Ja sillä ei ole väliä, mikä murtoluvussa on suurempi - osoittaja vai nimittäjä, jos se on nimittäjä, käännämme sen ja toimimme kuvatulla tavalla. Tällä tavalla voimme pienentää mitä tahansa murto-osaa, kolmatta lähestymistapaa voidaan kutsua universaaliksi.

Tietenkään kaksi edellä käsiteltyä esimerkkiä eivät ole yksinkertaisia ​​esimerkkejä. Kokeillaan tätä tekniikkaa "yksinkertaisilla" jakeilla, joita olemme jo harkinneet:

Kaksi neljännestä.

Seitsemänkymmentäkaksi kuusikymmentäkymmentä. Osoittaja on suurempi kuin nimittäjä; sitä ei tarvitse kääntää:

Tietysti kolmatta lähestymistapaa sovellettiin sellaisiin yksinkertaisia ​​esimerkkejä vain vaihtoehtona. Menetelmä, kuten jo sanottiin, on universaali, mutta ei kätevä ja oikea kaikille jakeille, erityisesti yksinkertaisille.

Fraktioiden valikoima on suuri. On tärkeää, että ymmärrät periaatteet. Tiukat säännöt murtolukujen kanssa ei yksinkertaisesti voi työskennellä. Katsoimme, mietimme, kuinka olisi mukavampaa toimia, ja menimme eteenpäin. Harjoittelemalla taito tulee ja murskaat ne kuin siemeniä.

Johtopäätös:

Jos näet osoittajalle ja nimittäjälle yhteisen jakajan, käytä niitä vähentämään.

Jos osaat kertoa luvun nopeasti, kerro osoittaja ja nimittäjä ja vähennä sitten.

Jos et voi määrittää yhteistä jakajaa, käytä kolmatta lähestymistapaa.

* Murtolukujen pienentämiseksi on tärkeää hallita pelkistyksen periaatteet, ymmärtää murto-osan perusominaisuus, tuntea ratkaisutavat ja olla erittäin varovainen laskelmissa.

Ja muista! On tapana pienentää murto-osaa, kunnes se pysähtyy, eli pienentää sitä niin kauan kuin on yhteinen jakaja.

Ystävällisin terveisin Alexander Krutitskikh.