How to reduce fractions with different denominators. How to reduce a fraction? Rules for all situations

The reduction of fractions is necessary in order to bring the fraction to a simpler form, for example, in the answer obtained as a result of solving the expression.

Reduction of fractions, definition and formula.

What is fraction reduction? What does it mean to reduce a fraction?

Definition:
Fraction reduction- this is the division of the fraction numerator and denominator by the same positive number not equal to zero and one. As a result of the reduction, a fraction with a smaller numerator and denominator is obtained, equal to the previous fraction according to.

Fraction reduction formula main property rational numbers.

\(\frac(p \times n)(q \times n)=\frac(p)(q)\)

Consider an example:
Reduce the fraction \(\frac(9)(15)\)

Solution:
We can factorize a fraction into prime factors and reduce the common factors.

\(\frac(9)(15)=\frac(3 \times 3)(5 \times 3)=\frac(3)(5) \times \color(red) (\frac(3)(3) )=\frac(3)(5) \times 1=\frac(3)(5)\)

Answer: after reduction we got the fraction \(\frac(3)(5)\). According to the main property of rational numbers, the initial and resulting fractions are equal.

\(\frac(9)(15)=\frac(3)(5)\)

How to reduce fractions? Reduction of a fraction to an irreducible form.

In order for us to get an irreducible fraction as a result, we need find the largest common divisor(GCD) for the numerator and denominator of a fraction.

There are several ways to find the GCD, we will use the decomposition of numbers into prime factors in the example.

Get the irreducible fraction \(\frac(48)(136)\).

Solution:
Find GCD(48, 136). Let's write the numbers 48 and 136 into prime factors.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
GCD(48, 136)= 2⋅2⋅2=6

\(\frac(48)(136)=\frac(\color(red) (2 \times 2 \times 2) \times 2 \times 3)(\color(red) (2 \times 2 \times 2) \times 17)=\frac(\color(red) (6) \times 2 \times 3)(\color(red) (6) \times 17)=\frac(2 \times 3)(17)=\ frac(6)(17)\)

The rule for reducing a fraction to an irreducible form.

Find the greatest common divisor for the numerator and denominator.
You need to divide the numerator and denominator by the greatest common divisor as a result of division to get an irreducible fraction.

Example:
Reduce the fraction \(\frac(152)(168)\).

Solution:
Find GCD(152, 168). Let's write the numbers 152 and 168 into prime factors.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
gcd(152, 168)= 2⋅2⋅2=6

\(\frac(152)(168)=\frac(\color(red) (6) \times 19)(\color(red) (6) \times 21)=\frac(19)(21)\)

Answer: \(\frac(19)(21)\) is an irreducible fraction.

Abbreviation of an improper fraction.

How to cut improper fraction?
The rules for reducing fractions for proper and improper fractions are the same.

Consider an example:
Reduce the improper fraction \(\frac(44)(32)\).

Solution:
Let's write the numerator and denominator into prime factors. And then we reduce the common factors.

\(\frac(44)(32)=\frac(\color(red) (2 \times 2 ) \times 11)(\color(red) (2 \times 2 ) \times 2 \times 2 \times 2 )=\frac(11)(2 \times 2 \times 2)=\frac(11)(8)\)

Reduction of mixed fractions.

Mixed fractions according to the same rules as common fractions. The only difference is that we can do not touch the whole part, but reduce the fractional part or Convert a mixed fraction to an improper fraction, reduce and convert back to a proper fraction.

Consider an example:
Reduce the mixed fraction \(2\frac(30)(45)\).

Solution:
Let's solve it in two ways:
First way:
We will write the fractional part into prime factors, and we will not touch the integer part.

\(2\frac(30)(45)=2\frac(2 \times \color(red) (5 \times 3))(3 \times \color(red) (5 \times 3))=2\ frac(2)(3)\)

Second way:
First we translate into an improper fraction, and then we write it into prime factors and reduce it. Convert the resulting improper fraction to a proper one.

\(2\frac(30)(45)=\frac(45 \times 2 + 30)(45)=\frac(120)(45)=\frac(2 \times \color(red) (5 \times 3) \times 2 \times 2)(3 \times \color(red) (3 \times 5))=\frac(2 \times 2 \times 2)(3)=\frac(8)(3)= 2\frac(2)(3)\)

Related questions:
Can fractions be reduced when adding or subtracting?
Answer: no, you must first add or subtract fractions according to the rules, and only then reduce. Consider an example:

Evaluate the expression \(\frac(50+20-10)(20)\) .

Solution:
They often make the mistake of reducing the same numbers in the numerator and denominator in our case, the number 20, but they cannot be reduced until you perform addition and subtraction.

\(\frac(50+\color(red) (20)-10)(\color(red) (20))=\frac(60)(20)=\frac(3 \times 20)(20)= \frac(3)(1)=3\)

By what number can you reduce a fraction?
Answer: You can reduce a fraction by the greatest common divisor or the usual divisor of the numerator and denominator. For example, the fraction \(\frac(100)(150)\).

Let's write the numbers 100 and 150 into prime factors.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
The greatest common divisor will be the number of gcd(100, 150)= 2⋅5⋅5=50

\(\frac(100)(150)=\frac(2 \times 50)(3 \times 50)=\frac(2)(3)\)

We got the irreducible fraction \(\frac(2)(3)\).

But it is not necessary to always divide by GCD, an irreducible fraction is not always needed, you can reduce the fraction by a simple divisor of the numerator and denominator. For example, the number 100 and 150 have a common divisor 2. Let's reduce the fraction \(\frac(100)(150)\) by 2.

\(\frac(100)(150)=\frac(2 \times 50)(2 \times 75)=\frac(50)(75)\)

We got the reduced fraction \(\frac(50)(75)\).

What fractions can be reduced?
Answer: You can reduce fractions in which the numerator and denominator have a common divisor. For example, the fraction \(\frac(4)(8)\). The number 4 and 8 have a number by which they are both divisible by this number 2. Therefore, such a fraction can be reduced by the number 2.

Example:
Compare two fractions \(\frac(2)(3)\) and \(\frac(8)(12)\).

These two fractions are equal. Consider the fraction \(\frac(8)(12)\) in detail:

\(\frac(8)(12)=\frac(2 \times 4)(3 \times 4)=\frac(2)(3) \times \frac(4)(4)=\frac(2) (3) \times 1=\frac(2)(3)\)

From here we get, \(\frac(8)(12)=\frac(2)(3)\)

Two fractions are equal if and only if one of them is obtained by reducing the other fraction by a common factor of the numerator and denominator.

Example:
Reduce the following fractions if possible: a) \(\frac(90)(65)\) b) \(\frac(27)(63)\) c) \(\frac(17)(100)\) d) \(\frac(100)(250)\)

Solution:
a) \(\frac(90)(65)=\frac(2 \times \color(red) (5) \times 3 \times 3)(\color(red) (5) \times 13)=\frac (2 \times 3 \times 3)(13)=\frac(18)(13)\)
b) \(\frac(27)(63)=\frac(\color(red) (3 \times 3) \times 3)(\color(red) (3 \times 3) \times 7)=\frac (3)(7)\)
c) \(\frac(17)(100)\) irreducible fraction
d) \(\frac(100)(250)=\frac(\color(red) (2 \times 5 \times 5) \times 2)(\color(red) (2 \times 5 \times 5) \ times 5)=\frac(2)(5)\)

With the help of fractions, the same part of a whole object can be written in different ways.

Half of the circle is shaded in the figure

Thus, all these fractions are equal.

For convenience, an additional factor is written on the slash to the right above the fraction.

Let's go back to our fractions and write them in a different order.

A fraction equal to a given one can be obtained if the numerator and denominator of the fraction are simultaneously divided by the same number that is not equal to zero.

This transformation of a fraction is called fraction reduction.

The reduction of a fraction is usually written as follows.

The numerator and denominator are crossed out with dashes, and next to them the results of dividing (quotients) of the numerator and denominator by the same number are written.

The number by which the numerator and denominator were divided is kept in mind.

In our example, we reduced (that is, divided both the numerator and denominator) the fraction by two, which we kept in mind.

Fraction reduction can be carried out sequentially.

Basic property of a fraction

We formulate the main property of a fraction.

If the numerator and denominator of a fraction are multiplied or divided by the same number that is not equal to zero, then a fraction equal to the given one will be obtained.

Let's write this property in the form of literal expressions.

, where "a", "b" and "k" are natural numbers.

Reduction of fractions, rule and examples of reduction of fractions.

In this article, we will analyze in detail how fraction reduction. First, let's talk about what is called fraction reduction. After that, let's talk about reducing a reducible fraction to an irreducible form. Next, we get the rule for reducing fractions and, finally, consider examples of the application of this rule.

Page navigation.

What does it mean to reduce a fraction?

We know that ordinary fractions are subdivided into reducible and irreducible fractions. From the names, you can guess that the reducible fractions can be reduced, but the irreducible ones cannot.

What does it mean to reduce a fraction? Reduce fraction is to divide its numerator and denominator by their positive and non-one common divisor. It is clear that as a result of fraction reduction, a new fraction is obtained with a smaller numerator and denominator, and, due to the main property of the fraction, the resulting fraction is equal to the original one.

For example, let's reduce the common fraction 8/24 by dividing its numerator and denominator by 2. In other words, let's reduce the fraction 8/24 by 2. Since 8:2=4 and 24:2=12, as a result of this reduction, the fraction 4/12 is obtained, which is equal to the original fraction 8/24 (see equal and unequal fractions). As a result, we have .

Reduction of ordinary fractions to irreducible form

Usually, the end goal of fraction reduction is to obtain an irreducible fraction that is equal to the original reducible fraction. This goal can be achieved by reducing the original reduced fraction by the greatest common divisor of its numerator and denominator. This reduction always results in an irreducible fraction. Indeed, fraction is irreducible, since it is known from the properties of gcd that and - mutually prime numbers. Here we say that the greatest common divisor of the numerator and denominator of a fraction is the largest number by which this fraction can be reduced.

So, reduction of an ordinary fraction to an irreducible form consists in dividing the numerator and denominator of the original reduced fraction by their GCD.

Let's analyze an example, for which we return to the fraction 8/24 and reduce it by the greatest common divisor of the numbers 8 and 24, which is equal to 8. Since 8:8=1 and 24:8=3, we arrive at the irreducible fraction 1/3. So, .

Note that the phrase “reduce the fraction” often means reducing the original fraction to an irreducible form. In other words, fraction reduction is very often referred to as dividing the numerator and denominator by their greatest common divisor (and not by any of their common divisors).

How to reduce a fraction? Rule and examples of fraction reduction

It remains only to analyze the rule for reducing fractions, which explains how to reduce this fraction.

Fraction reduction rule consists of two steps:

firstly, the GCD of the numerator and denominator of the fraction is found;
secondly, the numerator and denominator of the fraction are divided by their GCD, which gives an irreducible fraction equal to the original one.

Let's analyze fraction reduction example according to the given rule.

www.cleverstudents.ru

Fraction reduction. What does it mean to reduce a fraction?

The reduction of fractions is necessary in order to bring the fraction to a simpler form, for example, in the answer obtained as a result of solving the expression.

Reduction of fractions, definition and formula.

What is fraction reduction? What does it mean to reduce a fraction?

Fraction reduction formula basic property of rational numbers.

Consider an example:
Reduce the fraction \(\frac \)

Solution:
We can factorize a fraction into prime factors and reduce the common factors.

Answer: after the reduction, we got the fraction \(\frac \). According to the main property of rational numbers, the initial and resulting fractions are equal.

How to reduce fractions? Reduction of a fraction to an irreducible form.

In order for us to get an irreducible fraction as a result, we need find the greatest common divisor (gcd) for the numerator and denominator of a fraction.

There are several ways to find the GCD, we will use the decomposition of numbers into prime factors in the example.

Get the irreducible fraction \(\frac \).

Solution:
Find GCD(48, 136). Let's write the numbers 48 and 136 into prime factors.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
GCD(48, 136)= 2⋅2⋅2=6

The rule for reducing a fraction to an irreducible form.

Find the greatest common divisor for the numerator and denominator.
You need to divide the numerator and denominator by the greatest common divisor as a result of division to get an irreducible fraction.

Example:
Reduce the fraction \(\frac \).

Solution:
Find GCD(152, 168). Let's write the numbers 152 and 168 into prime factors.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
gcd(152, 168)= 2⋅2⋅2=6

Answer: \(\frac \) is an irreducible fraction.

Abbreviation of an improper fraction.

How to reduce an improper fraction?
The rules for reducing fractions for proper and improper fractions are the same.

Consider an example:
Reduce the improper fraction \(\frac \).

Solution:
Let's write the numerator and denominator into prime factors. And then we reduce the common factors.

Reduction of mixed fractions.

Mixed fractions follow the same rules as ordinary fractions. The only difference is that we can do not touch the whole part, but reduce the fractional part or Convert a mixed fraction to an improper fraction, reduce and convert back to a proper fraction.

Consider an example:
Reduce the mixed fraction \(2\frac \).

Solution:
Let's solve it in two ways:
First way:
We will write the fractional part into prime factors, and we will not touch the integer part.

Second way:
First we translate into an improper fraction, and then we write it into prime factors and reduce it. Convert the resulting improper fraction to a proper one.

Solution:
They often make the mistake of reducing the same numbers in the numerator and denominator in our case, the number 20, but they cannot be reduced until you perform addition and subtraction.

Let's write the numbers 100 and 150 into prime factors.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
The greatest common divisor will be the number of gcd(100, 150)= 2⋅5⋅5=50

We got the irreducible fraction \(\frac \).

We got the reduced fraction \(\frac \).

What fractions can be reduced?
Answer: You can reduce fractions in which the numerator and denominator have a common divisor. For example, the fraction \(\frac \). The number 4 and 8 have a number by which they are both divisible by this number 2. Therefore, such a fraction can be reduced by the number 2.

Example:
Compare two fractions \(\frac \) and \(\frac \).

These two fractions are equal. Consider the fraction \(\frac \) in detail:

Two fractions are equal if and only if one of them is obtained by reducing the other fraction by a common factor of the numerator and denominator.

Example:
Reduce the following fractions if possible: a) \(\frac \) b) \(\frac \) c) \(\frac \) d) \(\frac \)

Operations with common fractions

Fraction expansion. Fraction reduction. Fraction comparison.

Reduction to a common denominator. Addition and subtraction fractions.

Multiplication of fractions. Division of fractions .

Fraction expansion. The value of a fraction does not change if its numerator and denominator are multiplied by the same non-zero number. fraction expansion. For example,

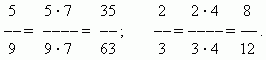
Fraction reduction. The value of a fraction does not change if its numerator and denominator are divided by the same non-zero number.. This transformation is called fraction reduction. For example,

Fraction comparison. Of two fractions with the same numerator, the larger one is the one with the smaller denominator:

Of two fractions with the same denominators, the one with the larger numerator is greater:

To compare fractions that have different numerators and denominators, you need to expand them to bring them to a common denominator.

EXAMPLE Compare two fractions:

We expand the first fraction by the denominator of the second, and the second by the denominator of the first:

The transformation used here is called reducing fractions to a common denominator.

Addition and subtraction of fractions. If the denominators of fractions are the same, then in order to add fractions, you need to add their numerators, and in order to subtract fractions, you need to subtract their numerators (in the same order). The resulting sum or difference will be the numerator of the result; the denominator will remain the same. If the denominators of the fractions are different, you must first reduce the fractions to a common denominator. When adding mixed numbers, their integer and fractional parts are added separately. When subtracting mixed numbers, we recommend that you first convert them to the form of improper fractions, then subtract from one another, and then again reduce the result, if necessary, to the form of a mixed number.

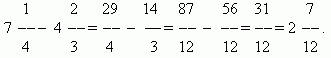
Multiplication of fractions. To multiply a number by a fraction means to multiply it by the numerator and divide the product by the denominator. Hence we have general rule multiplying fractions: to multiply fractions, you need to multiply their numerators and denominators separately and divide the first product by the second.

EXAMPLE

Division of fractions. To divide a number by a fraction, you need to multiply that number by its reciprocal.. This rule follows from the definition of division (see section "Arithmetic operations").

EXAMPLE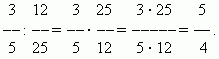

Multiplication and division of fractions

Last time we learned how to add and subtract fractions (see the lesson "Adding and subtracting fractions"). The most difficult moment in those actions was bringing fractions to a common denominator.

Now it's time to deal with multiplication and division. Good news is that these operations are even simpler than addition and subtraction. To begin with, consider the simplest case, when there are two positive fractions without a distinguished integer part.

To multiply two fractions, you need to multiply their numerators and denominators separately. The first number will be the numerator of the new fraction, and the second will be the denominator.

To divide two fractions, you need to multiply the first fraction by the "inverted" second.

From the definition it follows that the division of fractions is reduced to multiplication. To flip a fraction, just swap the numerator and denominator. Therefore, the entire lesson we will consider mainly multiplication.

As a result of multiplication, a reduced fraction can arise (and often does arise) - of course, it must be reduced. If, after all the reductions, the fraction turned out to be incorrect, the whole part should be distinguished in it. But what exactly will not happen with multiplication is reduction to a common denominator: no crosswise methods, maximum factors and least common multiples.

Multiplication of fractions with an integer part and negative fractions

If there is an integer part in the fractions, they must be converted to improper ones - and only then multiplied according to the schemes outlined above.

If there is a minus in the numerator of a fraction, in the denominator or in front of it, it can be taken out of the limits of multiplication or removed altogether according to the following rules:

Plus times minus gives minus;
Two negatives make an affirmative.

Until now, these rules have only been encountered when adding and subtracting negative fractions, when it was required to get rid of the whole part. For a product, they can be generalized in order to “burn” several minuses at once:

We cross out the minuses in pairs until they completely disappear. In an extreme case, one minus can survive - the one that did not find a match;
If there are no minuses left, the operation is completed - you can start multiplying. If the last minus is not crossed out, since it did not find a pair, we take it out of the limits of multiplication. You get a negative fraction.

A task. Find the value of the expression:

We translate all fractions into improper ones, and then we take out the minuses outside the limits of multiplication. What remains is multiplied according to the usual rules. We get:

Let me remind you once again that the minus that stands in front of the fraction with the highlighted whole part, refers specifically to the whole fraction, and not just to its integer part (this applies to the last two examples).

Also pay attention to negative numbers: When multiplied, they are enclosed in parentheses. This is done in order to separate the minuses from the multiplication signs and make the whole notation more accurate.

Reducing fractions on the fly

Multiplication is a very laborious operation. The numbers here are quite large, and to simplify the task, you can try to reduce the fraction even more before multiplication. Indeed, in essence, the numerators and denominators of fractions are ordinary factors, and, therefore, they can be reduced using the basic property of a fraction. Take a look at the examples:

By definition we have:

In all examples, the numbers that have been reduced and what is left of them are marked in red.

Please note: in the first case, the multipliers were reduced completely. Units remained in their place, which, generally speaking, can be omitted. In the second example, it was not possible to achieve a complete reduction, but the total amount of calculations still decreased.

However, in no case do not use this technique when adding and subtracting fractions! Yes, sometimes there are similar numbers that you just want to reduce. Here, look:

You can't do that!

The error occurs due to the fact that when adding a fraction, the sum appears in the numerator of a fraction, and not the product of numbers. Therefore, it is impossible to apply the main property of a fraction, since this property deals specifically with the multiplication of numbers.

There is simply no other reason to reduce fractions, so the correct solution to the previous problem looks like this:

As you can see, the correct answer turned out to be not so beautiful. In general, be careful.

To understand how to reduce fractions, let's first look at one example.

To reduce a fraction means to divide the numerator and denominator by the same. Both 360 and 420 end in a number, so we can reduce this fraction by 2. In the new fraction, both 180 and 210 are also divisible by 2, we reduce this fraction by 2. In the numbers 90 and 105, the sum of the digits is divisible by 3, so both these numbers are divisible by 3, we reduce the fraction by 3. In the new fraction, 30 and 35 end in 0 and 5, which means that both numbers are divisible by 5, so we reduce the fraction by 5. The resulting fraction, six sevenths, is irreducible. This is the final answer.

We can arrive at the same answer in a different way.

Both 360 and 420 end in zero, which means they are divisible by 10. We reduce the fraction by 10. In the new fraction, both the numerator 36 and the denominator 42 are divided by 2. We reduce the fraction by 2. In the next fraction, both the numerator 18 and the denominator 21 are divided by 3, which means we reduce the fraction by 3. We came to the result - six sevenths.

And one more solution.

Next time we will consider examples of reduction of fractions.

Children at school learn the rules for reducing fractions in 6th grade. In this article, we will first tell you what this action means, then we will explain how to translate a reducible fraction into an irreducible one. The next item will be the rules for reducing fractions, and then we will gradually get to the examples.

What does "reduce a fraction" mean?

So we all know that common fractions are divided into two groups: reducible and irreducible. Already by the names it can be understood that those that are contractible are reduced, and those that are irreducible are not reduced.

To reduce a fraction is to divide its denominator and numerator by their (other than one) positive divisor. The result, of course, is a new fraction with a smaller denominator and numerator. The resulting fraction will be equal to the original fraction.

It is worth noting that in math books with the task "reduce the fraction", this means that you need to bring the original fraction to this irreducible form. If to speak in simple terms, then dividing the denominator and numerator by their greatest common divisor is the reduction.

How to reduce a fraction. Rules for reducing fractions (Grade 6)

So there are only two rules here.

The first rule for reducing fractions is to first find the greatest common divisor of the denominator and numerator of your fraction.
Second rule: Divide the denominator and numerator by the greatest common divisor to end up with an irreducible fraction.

How to reduce an improper fraction?

The rules for reducing fractions are identical to the rules for reducing improper fractions.

In order to reduce an improper fraction, first you will need to paint the denominator and numerator into simple factors, and only then reduce the common factors.

Reduction of mixed fractions

The rules for reducing fractions also apply to the reduction of mixed fractions. There is only a small difference: we can not touch the whole part, but reduce the fractional or mixed fraction into an improper one, then reduce it and again convert it into a proper fraction.

There are two ways to reduce mixed fractions.

First: to paint the fractional part into prime factors and then do not touch the integer part.

The second way: first translate into an improper fraction, paint on the usual factors, then reduce the fraction. Convert the received improper fraction to the proper one.

Examples can be seen in the photo above.

We really hope that we could help you and your children. After all, in the classroom they are very often inattentive, so you have to work harder at home on your own.

So we got to the reduction. The basic property of a fraction is applied here. BUT! Not so simple. With many fractions (including from school course) can be easily dispensed with. And if you take fractions "more abruptly"? Let's find out more! I recommend looking at materials with fractions.

So, we already know that the numerator and denominator of a fraction can be multiplied and divided by the same number, the fraction will not change from this. Consider three approaches:

First approach.

To reduce, divide the numerator and denominator by a common divisor. Consider examples:

Let's shorten:

In the above examples, we immediately see which divisors to take for reduction. The process is simple - we iterate over 2,3.4,5 and so on. In most examples of a school course, this is quite enough. But if there is a fraction:

Here the process with the selection of dividers can drag on for a long time;). Of course, such examples lie outside the school curriculum, but you need to be able to deal with them. Let's take a look at how this is done below. In the meantime, back to the reduction process.

As discussed above, in order to reduce the fraction, we carried out the division by the common divisor (s) we defined. Everything is correct! One has only to add signs of divisibility of numbers:

If the number is even then it is divisible by 2.

- if the number of the last two digits is divisible by 4, then the number itself is divisible by 4.

- if the sum of the digits that make up the number is divisible by 3, then the number itself is divisible by 3. For example, 125031, 1+2+5+0+3+1=12. Twelve is divisible by 3, so 123031 is divisible by 3.

- if the number ends with 5 or 0, then the number is divisible by 5.

- if the sum of the digits that make up the number is divisible by 9, then the number itself is divisible by 9. For example 625032 =.> 6+2+5+0+3+2=18. Eighteen is divisible by 9, so 623032 is divisible by 9.

Second approach.

In short, the essence, then in fact the whole action comes down to decomposing the numerator and denominator into factors and then reducing equal factors in the numerator and denominator (this approach is a consequence of the first approach):

Visually, in order not to get confused and not to make a mistake, equal multipliers are simply crossed out. The question is how to factorize a number? It is necessary to determine by enumeration all the divisors. This is a separate topic, it is simple, look at the information in a textbook or on the Internet. You will not encounter any great problems with the factorization of numbers that are present in the fractions of the school course.

Formally, the reduction principle can be written as follows:

Third approach.

Here is the most interesting for advanced and those who want to become one. Let's reduce the fraction 143/273. Try it yourself! Well, how quickly did it happen? And now look!

We turn it over (the numerator and denominator are interchanged). We divide the resulting fraction by a corner and translate it into mixed number, that is, we select the integer part:

Already easier. We see that the numerator and denominator can be reduced by 13:

And now do not forget to flip the fraction back again, let's write the whole chain:

Checked - it takes less time than searching and checking divisors. Let's go back to our two examples:

The first. We divide by a corner (not on a calculator), we get:

This fraction is simpler, of course, but there is again a problem with reduction. Now we separately analyze the fraction 1273/1463, turn it over:

It's already easier here. We can consider such a divisor as 19. The rest do not fit, it can be seen: 190:19= 10, 1273:19 = 67. Hooray! Let's write:

Next example. Let's cut 88179/2717.

We divide, we get:

Separately, we analyze the fraction 1235/2717, turn it over:

We can consider such a divisor as 13 (up to 13 are not suitable):

Numerator 247:13=19 Denominator 1235:13=95

*In the process, we saw another divisor equal to 19. It turns out that:

Now write down the original number:

And it doesn’t matter what will be more in the fraction - the numerator or the denominator, if the denominator, then we turn over and act as described. Thus, we can reduce any fraction, the third approach can be called universal.

Of course, the two examples discussed above are not simple examples. Let's try this technology on the "simple" fractions we have already considered:

Two fourths.

Seventy-two sixties. The numerator is greater than the denominator, no need to flip:

Of course, the third approach was applied to such simple examples just as an alternative. The method, as already mentioned, is universal, but not convenient and correct for all fractions, especially for simple ones.

The variety of fractions is great. It is important that you learn exactly the principles. Strict rule for working with fractions is simply not. We looked, figured out how it would be more convenient to act and move forward. With practice, the skill will come and you will click them like seeds.

Conclusion:

If you see a common divisor(s) for the numerator and denominator, then use them to reduce.

If you know how to quickly factorize a number, then decompose the numerator and denominator, then reduce.

If you can’t determine the common divisor in any way, then use the third approach.

*To reduce fractions, it is important to learn the principles of reduction, understand the basic property of a fraction, know the approaches to solving, and be extremely careful when calculating.

And remember! It is customary to reduce a fraction to the stop, that is, to reduce it while there is a common divisor.

Sincerely, Alexander Krutitskikh.