Abbreviation of an improper fraction. Online calculator for reducing algebraic fractions with a detailed solution allows you to reduce a fraction and convert an improper fraction to a proper fraction

If we need to divide 497 by 4, then when dividing, we will see that 497 is not divisible by 4, i.e. remains the remainder of the division. In such cases, it is said that division with remainder, and the solution is written as follows:
497: 4 = 124 (1 remainder).

The division components on the left side of the equality are called the same as in division without a remainder: 497 - dividend, 4 - divider. The result of division when dividing with a remainder is called incomplete private. In our case, this number is 124. And finally, the last component, which is not in the usual division, is remainder. When there is no remainder, one number is said to be divided by another. without a trace, or completely. It is believed that with such a division, the remainder is zero. In our case, the remainder is 1.

The remainder is always less than the divisor.

You can check when dividing by multiplying. If, for example, there is an equality 64: 32 = 2, then the check can be done like this: 64 = 32 * 2.

Often in cases where division with a remainder is performed, it is convenient to use the equality
a \u003d b * n + r,
where a is the dividend, b is the divisor, n is the partial quotient, r is the remainder.

The quotient of division of natural numbers can be written as a fraction.

The numerator of a fraction is the dividend, and the denominator is the divisor.

Since the numerator of a fraction is the dividend and the denominator is the divisor, believe that the line of a fraction means the action of division. Sometimes it is convenient to write division as a fraction without using the ":" sign.

The quotient of division of natural numbers m and n can be written as a fraction \(\frac(m)(n) \), where the numerator m is the dividend, and the denominator n is the divisor:
\(m:n = \frac(m)(n) \)

The following rules are correct:

To get a fraction \(\frac(m)(n) \), you need to divide the unit by n equal parts(shares) and take m such parts.

To get the fraction \(\frac(m)(n) \), you need to divide the number m by the number n.

To find a part of a whole, you need to divide the number corresponding to the whole by the denominator and multiply the result by the numerator of the fraction that expresses this part.

To find a whole by its part, you need to divide the number corresponding to this part by the numerator and multiply the result by the denominator of the fraction that expresses this part.

If both the numerator and the denominator of a fraction are multiplied by the same number (except zero), the value of the fraction will not change:
\(\large \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)

If both the numerator and the denominator of a fraction are divided by the same number (except zero), the value of the fraction will not change:
\(\large \frac(a)(b) = \frac(a: m)(b: m) \)
This property is called basic property of a fraction.

The last two transformations are called fraction reduction.

If fractions need to be represented as fractions with the same denominator, then such an action is called reducing fractions to a common denominator.

Proper and improper fractions. mixed numbers

You already know that a fraction can be obtained by dividing a whole into equal parts and taking several such parts. For example, the fraction \(\frac(3)(4) \) means three-fourths of one. In many of the problems in the previous section, fractions were used to denote part of a whole. Common sense suggests that the part must always be less than the whole, but then what about fractions such as \(\frac(5)(5) \) or \(\frac(8)(5) \)? It is clear that this is no longer part of the unit. This is probably why such fractions, in which the numerator is greater than or equal to the denominator, are called improper fractions. The remaining fractions, i.e., fractions in which the numerator is less than the denominator, are called proper fractions.

As you know, any ordinary fraction, both proper and improper, can be considered as the result of dividing the numerator by the denominator. Therefore, in mathematics, unlike in ordinary language, the term "improper fraction" does not mean that we did something wrong, but only that this fraction has a numerator greater than or equal to its denominator.

If a number consists of an integer part and a fraction, then such fractions are called mixed.

For example:
\(5:3 = 1\frac(2)(3) \) : 1 - whole part, and \(\frac(2)(3) \) is the fractional part.

If the numerator \(\frac(a)(b) \) is divisible by natural number n, then to divide this fraction by n, you need to divide its numerator by this number:
\(\large \frac(a)(b) : n = \frac(a:n)(b) \)

If the numerator of the fraction \(\frac(a)(b) \) is not divisible by a natural number n, then to divide this fraction by n, you need to multiply its denominator by this number:
\(\large \frac(a)(b) : n = \frac(a)(bn) \)

Note that the second rule is also valid when the numerator is divisible by n. Therefore, we can use it when it is difficult at first glance to determine whether the numerator of a fraction is divisible by n or not.

Actions with fractions. Addition of fractions.

With fractional numbers, as with natural numbers, you can perform arithmetic operations. Let's look at adding fractions first. It's easy to add fractions with the same denominators. Find, for example, the sum of \(\frac(2)(7) \) and \(\frac(3)(7) \). It is easy to understand that \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \)

To add fractions with the same denominators, you need to add their numerators, and leave the denominator the same.

Using letters, the rule for adding fractions with the same denominators can be written as follows:
\(\large \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)

If you want to add fractions with different denominators, then they must first be reduced to a common denominator. For example:
\(\large \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3 ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)

For fractions, as well as for natural numbers, the commutative and associative properties of addition are valid.

Addition of mixed fractions

Recordings such as \(2\frac(2)(3) \) are called mixed fractions. The number 2 is called whole part mixed fraction, and the number \(\frac(2)(3) \) is its fractional part. The entry \(2\frac(2)(3) \) is read like this: "two and two thirds".

Dividing the number 8 by the number 3 gives two answers: \(\frac(8)(3) \) and \(2\frac(2)(3) \). They express the same fractional number, i.e. \(\frac(8)(3) = 2 \frac(2)(3) \)

Thus, the improper fraction \(\frac(8)(3) \) is represented as a mixed fraction \(2\frac(2)(3) \). In such cases, they say that from an improper fraction singled out the whole.

Subtraction of fractions (fractional numbers)

Subtraction fractional numbers, as well as natural ones, is determined on the basis of the operation of addition: subtracting another from one number means finding a number that, when added to the second, gives the first. For example:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) since \(\frac(7)(9)+\frac(1)(9 ) = \frac(8)(9) \)

The rule for subtracting fractions with like denominators is similar to the rule for adding such fractions:
To find the difference between fractions with the same denominators, subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator the same.

Using letters, this rule is written as follows:
\(\large \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)

Multiplication of fractions

To multiply a fraction by a fraction, you need to multiply their numerators and denominators and write the first product as the numerator and the second as the denominator.

Using letters, the rule for multiplying fractions can be written as follows:
\(\large \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)

Using the formulated rule, it is possible to multiply a fraction by a natural number, by a mixed fraction, and also multiply mixed fractions. To do this, you need to write a natural number as a fraction with a denominator of 1, a mixed fraction as an improper fraction.

The result of multiplication should be simplified (if possible) by reducing the fraction and highlighting the integer part of the improper fraction.

For fractions, as well as for natural numbers, the commutative and associative properties of multiplication are valid, as well as the distributive property of multiplication with respect to addition.

Division of fractions

Take the fraction \(\frac(2)(3) \) and “flip” it by swapping the numerator and denominator. We get the fraction \(\frac(3)(2) \). This fraction is called reverse fractions \(\frac(2)(3) \).

If we now “reverse” the fraction \(\frac(3)(2) \), then we get the original fraction \(\frac(2)(3) \). Therefore, fractions such as \(\frac(2)(3) \) and \(\frac(3)(2) \) are called mutually inverse.

For example, the fractions \(\frac(6)(5) \) and \(\frac(5)(6) \), \(\frac(7)(18) \) and \(\frac (18)(7) \).

Using letters, mutually inverse fractions can be written as follows: \(\frac(a)(b) \) and \(\frac(b)(a) \)

It is clear that the product of reciprocal fractions is 1. For example: \(\frac(2)(3) \cdot \frac(3)(2) =1 \)

Using reciprocal fractions, division of fractions can be reduced to multiplication.

The rule for dividing a fraction by a fraction:
To divide one fraction by another, you need to multiply the dividend by the reciprocal of the divisor.

Using letters, the rule for dividing fractions can be written as follows:
\(\large \frac(a)(b) : \frac(c)(d) = \frac(a)(b) \cdot \frac(d)(c) \)

If the dividend or divisor is a natural number or a mixed fraction, then in order to use the rule for dividing fractions, it must first be represented as an improper fraction.

With the help of fractions, the same part of a whole object can be written in different ways.

Half of the circle is shaded in the figure

Thus, all these fractions are equal.

For convenience, an additional factor is written on the slash to the right above the fraction.

Let's go back to our fractions and write them in a different order.

A fraction equal to a given one can be obtained if the numerator and denominator of the fraction are simultaneously divided by the same number that is not equal to zero.

This transformation of a fraction is called fraction reduction.

The reduction of a fraction is usually written as follows.

The numerator and denominator are crossed out with dashes, and next to them the results of dividing (quotients) of the numerator and denominator by the same number are written.

The number by which the numerator and denominator were divided is kept in mind.

In our example, we reduced (that is, divided both the numerator and denominator) the fraction by two, which we kept in mind.

Fraction reduction can be carried out sequentially.

Basic property of a fraction

We formulate the main property of a fraction.

If the numerator and denominator of a fraction are multiplied or divided by the same number that is not equal to zero, then a fraction equal to the given one will be obtained.

Let's write this property in the form of literal expressions.

, where "a", "b" and "k" are natural numbers.

Reduction of fractions, rule and examples of reduction of fractions.

In this article, we will analyze in detail how fraction reduction. First, let's talk about what is called fraction reduction. After that, let's talk about reducing a reducible fraction to an irreducible form. Next, we get the rule for reducing fractions and, finally, consider examples of the application of this rule.

Page navigation.

What does it mean to reduce a fraction?

We know that ordinary fractions are subdivided into reducible and irreducible fractions. From the names, you can guess that the reducible fractions can be reduced, but the irreducible ones cannot.

What does it mean to reduce a fraction? Reduce fraction- this means dividing its numerator and denominator by their positive and non-one common divisor. It is clear that as a result of fraction reduction, a new fraction is obtained with a smaller numerator and denominator, and, due to the main property of the fraction, the resulting fraction is equal to the original one.

For example, let's reduce the common fraction 8/24 by dividing its numerator and denominator by 2. In other words, let's reduce the fraction 8/24 by 2. Since 8:2=4 and 24:2=12, as a result of this reduction, the fraction 4/12 is obtained, which is equal to the original fraction 8/24 (see equal and unequal fractions). As a result, we have .

Reduction of ordinary fractions to irreducible form

Usually, the end goal of fraction reduction is to obtain an irreducible fraction that is equal to the original reducible fraction. This goal can be achieved by reducing the original reduced fraction by the greatest common divisor of its numerator and denominator. This reduction always results in an irreducible fraction. Indeed, fraction is irreducible, since it is known from the properties of gcd that and - mutually prime numbers. Here we say that the greatest common divisor of the numerator and denominator of a fraction is the largest number by which this fraction can be reduced.

So, reduction of an ordinary fraction to an irreducible form consists in dividing the numerator and denominator of the original reduced fraction by their GCD.

Let's analyze an example, for which we return to the fraction 8/24 and reduce it by the greatest common divisor of the numbers 8 and 24, which is equal to 8. Since 8:8=1 and 24:8=3, we arrive at the irreducible fraction 1/3. So, .

Note that the phrase “reduce the fraction” often means reducing the original fraction to an irreducible form. In other words, fraction reduction is very often referred to as dividing the numerator and denominator by their greatest common divisor (and not by any of their common divisors).

How to reduce a fraction? Rule and examples of fraction reduction

It remains only to analyze the rule for reducing fractions, which explains how to reduce this fraction.

Fraction reduction rule consists of two steps:

• firstly, the GCD of the numerator and denominator of the fraction is found;
• secondly, the numerator and denominator of the fraction are divided by their GCD, which gives an irreducible fraction equal to the original one.

Let's analyze fraction reduction example according to the given rule.

www.cleverstudents.ru

Fraction reduction. What does it mean to reduce a fraction?

The reduction of fractions is necessary in order to bring the fraction to a simpler form, for example, in the answer obtained as a result of solving the expression.

Reduction of fractions, definition and formula.

What is fraction reduction? What does it mean to reduce a fraction?

Definition:
Fraction reduction- this is the division of the fraction numerator and denominator by the same positive number not equal to zero and one. As a result of the reduction, a fraction with a smaller numerator and denominator is obtained, equal to the previous fraction according to the main property rational numbers.

Fraction reduction formula basic property of rational numbers.

Consider an example:
Reduce the fraction \(\frac \)

Solution:
We can factorize a fraction into prime factors and reduce the common factors.

Answer: after the reduction, we got the fraction \(\frac \). According to the main property of rational numbers, the initial and resulting fractions are equal.

How to reduce fractions? Reduction of a fraction to an irreducible form.

In order for us to get an irreducible fraction as a result, we need find the greatest common divisor (gcd) for the numerator and denominator of a fraction.

There are several ways to find the GCD, we will use the decomposition of numbers into prime factors in the example.

Get the irreducible fraction \(\frac \).

Solution:
Find GCD(48, 136). Let's write the numbers 48 and 136 into prime factors.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
GCD(48, 136)= 2⋅2⋅2=6

The rule for reducing a fraction to an irreducible form.

1. Find the greatest common divisor for the numerator and denominator.
2. You need to divide the numerator and denominator by the greatest common divisor as a result of division to get an irreducible fraction.

Example:
Reduce the fraction \(\frac \).

Solution:
Find GCD(152, 168). Let's write the numbers 152 and 168 into prime factors.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
gcd(152, 168)= 2⋅2⋅2=6

Answer: \(\frac \) is an irreducible fraction.

Abbreviation of an improper fraction.

How to reduce an improper fraction?
The rules for reducing fractions for proper and improper fractions are the same.

Consider an example:
Reduce the improper fraction \(\frac \).

Solution:
Let's write the numerator and denominator into prime factors. And then we reduce the common factors.

Reduction of mixed fractions.

Mixed fractions follow the same rules as ordinary fractions. The only difference is that we can do not touch the whole part, but reduce the fractional part or Convert a mixed fraction to an improper fraction, reduce and convert back to a proper fraction.

Consider an example:
Reduce the mixed fraction \(2\frac \).

Solution:
Let's solve it in two ways:
First way:
We will write the fractional part into prime factors, and we will not touch the integer part.

Second way:
First we translate into an improper fraction, and then we write it into prime factors and reduce it. Convert the resulting improper fraction to a proper one.

Related questions:
Can fractions be reduced when adding or subtracting?
Answer: no, you must first add or subtract fractions according to the rules, and only then reduce. Consider an example:

Solution:
They often make the mistake of reducing the same numbers in the numerator and denominator in our case, the number 20, but they cannot be reduced until you perform addition and subtraction.

By what number can you reduce a fraction?
Answer: You can reduce a fraction by the greatest common divisor or the usual divisor of the numerator and denominator. For example, the fraction \(\frac \).

Let's write the numbers 100 and 150 into prime factors.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
The greatest common divisor will be the number of gcd(100, 150)= 2⋅5⋅5=50

We got the irreducible fraction \(\frac \).

But it is not necessary to always divide by GCD, an irreducible fraction is not always needed, you can reduce the fraction by a simple divisor of the numerator and denominator. For example, the number 100 and 150 have a common divisor 2. Let's reduce the fraction \(\frac \) by 2.

We got the reduced fraction \(\frac \).

What fractions can be reduced?
Answer: You can reduce fractions in which the numerator and denominator have a common divisor. For example, the fraction \(\frac \). The number 4 and 8 have a number by which they are both divisible by this number 2. Therefore, such a fraction can be reduced by the number 2.

Example:
Compare two fractions \(\frac \) and \(\frac \).

These two fractions are equal. Consider the fraction \(\frac \) in detail:

Two fractions are equal if and only if one of them is obtained by reducing the other fraction by a common factor of the numerator and denominator.

Example:
Reduce the following fractions if possible: a) \(\frac \) b) \(\frac \) c) \(\frac \) d) \(\frac \)

Operations with common fractions

Fraction expansion. Fraction reduction. Fraction comparison.

Reduction to a common denominator. Addition and subtraction fractions.

Multiplication of fractions. Division of fractions .

Fraction expansion. The value of a fraction does not change if its numerator and denominator are multiplied by the same non-zero number. fraction expansion. For example,



Fraction reduction. The value of a fraction does not change if its numerator and denominator are divided by the same non-zero number.. This transformation is called fraction reduction. For example,



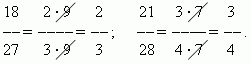
Fraction comparison. Of two fractions with the same numerator, the larger one is the one with the smaller denominator:



Of two fractions with the same denominators, the one with the larger numerator is greater:



To compare fractions that have different numerators and denominators, you need to expand them to bring them to a common denominator.

EXAMPLE Compare two fractions:

We expand the first fraction by the denominator of the second, and the second by the denominator of the first:

The transformation used here is called reducing fractions to a common denominator.

Addition and subtraction of fractions. If the denominators of fractions are the same, then in order to add fractions, you need to add their numerators, and in order to subtract fractions, you need to subtract their numerators (in the same order). The resulting sum or difference will be the numerator of the result; the denominator will remain the same. If the denominators of the fractions are different, you must first reduce the fractions to a common denominator. When adding mixed numbers, their integer and fractional parts are added separately. When subtracting mixed numbers, we recommend that you first convert them to the form of improper fractions, then subtract from one another, and then again reduce the result, if necessary, to the form of a mixed number.



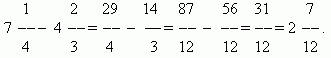
Multiplication of fractions. To multiply a number by a fraction means to multiply it by the numerator and divide the product by the denominator. Hence we have general rule multiplying fractions: to multiply fractions, you need to multiply their numerators and denominators separately and divide the first product by the second.

EXAMPLE

Division of fractions. To divide a number by a fraction, you need to multiply that number by its reciprocal.. This rule follows from the definition of division (see section "Arithmetic operations").

EXAMPLE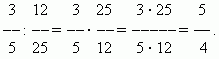

Multiplication and division of fractions

Last time we learned how to add and subtract fractions (see the lesson "Adding and subtracting fractions"). The most difficult moment in those actions was bringing fractions to a common denominator.

Now it's time to deal with multiplication and division. Good news is that these operations are even simpler than addition and subtraction. To begin with, consider the simplest case, when there are two positive fractions without a distinguished integer part.

To multiply two fractions, you need to multiply their numerators and denominators separately. The first number will be the numerator of the new fraction, and the second will be the denominator.

To divide two fractions, you need to multiply the first fraction by the "inverted" second.

From the definition it follows that the division of fractions is reduced to multiplication. To flip a fraction, just swap the numerator and denominator. Therefore, the entire lesson we will consider mainly multiplication.

As a result of multiplication, a reduced fraction can arise (and often does arise) - of course, it must be reduced. If, after all the reductions, the fraction turned out to be incorrect, the whole part should be distinguished in it. But what exactly will not happen with multiplication is reduction to a common denominator: no crosswise methods, maximum factors and least common multiples.



Multiplication of fractions with an integer part and negative fractions

If there is an integer part in the fractions, they must be converted to improper ones - and only then multiplied according to the schemes outlined above.

If there is a minus in the numerator of a fraction, in the denominator or in front of it, it can be taken out of the limits of multiplication or removed altogether according to the following rules:

1. Plus times minus gives minus;
2. Two negatives make an affirmative.

Until now, these rules have only been encountered when adding and subtracting negative fractions, when it was required to get rid of the whole part. For a product, they can be generalized in order to “burn” several minuses at once:

3. We cross out the minuses in pairs until they completely disappear. In an extreme case, one minus can survive - the one that did not find a match;
4. If there are no minuses left, the operation is completed - you can start multiplying. If the last minus is not crossed out, since it did not find a pair, we take it out of the limits of multiplication. You get a negative fraction.

A task. Find the value of the expression:

We translate all fractions into improper ones, and then we take out the minuses outside the limits of multiplication. What remains is multiplied according to the usual rules. We get:



Let me remind you once again that the minus that comes before a fraction with a highlighted integer part refers specifically to the entire fraction, and not just to its integer part (this applies to the last two examples).

Also pay attention to negative numbers: When multiplied, they are enclosed in parentheses. This is done in order to separate the minuses from the multiplication signs and make the whole notation more accurate.

Reducing fractions on the fly

Multiplication is a very laborious operation. The numbers here are quite large, and to simplify the task, you can try to reduce the fraction even more before multiplication. Indeed, in essence, the numerators and denominators of fractions are ordinary factors, and, therefore, they can be reduced using the basic property of a fraction. Take a look at the examples:



By definition we have:



In all examples, the numbers that have been reduced and what is left of them are marked in red.

Please note: in the first case, the multipliers were reduced completely. Units remained in their place, which, generally speaking, can be omitted. In the second example, it was not possible to achieve a complete reduction, but the total amount of calculations still decreased.

However, in no case do not use this technique when adding and subtracting fractions! Yes, sometimes there are similar numbers that you just want to reduce. Here, look:

You can't do that!

The error occurs due to the fact that when adding a fraction, the sum appears in the numerator of a fraction, and not the product of numbers. Therefore, it is impossible to apply the main property of a fraction, since this property deals specifically with the multiplication of numbers.

There is simply no other reason to reduce fractions, so the correct solution to the previous problem looks like this:

As you can see, the correct answer turned out to be not so beautiful. In general, be careful.

This article continues the theme of the transformation of algebraic fractions: consider such an action as the reduction of algebraic fractions. Let's define the term itself, formulate the abbreviation rule and analyze practical examples.

Yandex.RTB R-A-339285-1

Meaning of Algebraic Fraction Abbreviation

In the materials on the ordinary fraction, we considered its reduction. We have defined the reduction of a common fraction as dividing its numerator and denominator by a common factor.

Reducing an algebraic fraction is a similar operation.

Definition 1

Algebraic fraction reduction is the division of its numerator and denominator by a common factor. In this case, unlike the reduction of an ordinary fraction (only a number can be a common denominator), a polynomial, in particular, a monomial or a number, can serve as a common factor for the numerator and denominator of an algebraic fraction.

For example, the algebraic fraction 3 x 2 + 6 x y 6 x 3 y + 12 x 2 y 2 can be reduced by the number 3, as a result we get: x 2 + 2 x y 6 x 3 y + 12 x 2 y 2 . We can reduce the same fraction by the variable x, and this will give us the expression 3 x + 6 y 6 x 2 y + 12 x y 2 . It is also possible to reduce a given fraction by a monomial 3 x or any of the polynomials x + 2 y, 3 x + 6 y , x 2 + 2 x y or 3 x 2 + 6 x y.

The ultimate goal of reducing an algebraic fraction is a fraction of a simpler form, at best an irreducible fraction.

Are all algebraic fractions subject to reduction?

Again, from the materials on ordinary fractions, we know that there are reducible and irreducible fractions. Irreducible - these are fractions that do not have common factors of the numerator and denominator, other than 1.

With algebraic fractions, everything is the same: they may or may not have common factors of the numerator and denominator. The presence of common factors allows you to simplify the original fraction through reduction. When there are no common factors, it is impossible to optimize a given fraction by the reduction method.

In general cases, for a given type of fraction, it is quite difficult to understand whether it is subject to reduction. Of course, in some cases, the presence of a common factor of the numerator and denominator is obvious. For example, in the algebraic fraction 3 · x 2 3 · y it is quite clear that the common factor is the number 3 .

In a fraction - x · y 5 · x · y · z 3 we also immediately understand that it is possible to reduce it by x, or y, or by x · y. And yet, examples of algebraic fractions are much more common, when the common factor of the numerator and denominator is not so easy to see, and even more often - it is simply absent.

For example, we can reduce the fraction x 3 - 1 x 2 - 1 by x - 1, while the specified common factor is not in the record. But the fraction x 3 - x 2 + x - 1 x 3 + x 2 + 4 x + 4 cannot be reduced, since the numerator and denominator do not have a common factor.

Thus, the question of finding out the contractibility of an algebraic fraction is not so simple, and it is often easier to work with a fraction of a given form than to try to find out whether it is contractible. In this case, such transformations take place that in particular cases allow us to determine the common factor of the numerator and denominator or to conclude that the fraction is irreducible. We will analyze this issue in detail in the next paragraph of the article.

Algebraic fraction reduction rule

Algebraic fraction reduction rule consists of two consecutive steps:

• finding the common factors of the numerator and denominator;
• in the case of finding such, the implementation of the direct action of reducing the fraction.

The most convenient method for finding common denominators is to factorize the polynomials present in the numerator and denominator of a given algebraic fraction. This allows you to immediately visually see the presence or absence of common factors.

The very action of reducing an algebraic fraction is based on the main property of an algebraic fraction, expressed by the equality undefined , where a , b , c are some polynomials, and b and c are non-zero. The first step is to reduce the fraction to the form a c b c , in which we immediately notice the common factor c . The second step is to perform the reduction, i.e. transition to a fraction of the form a b .

Typical examples

Despite some obviousness, let's clarify about special case when the numerator and denominator of an algebraic fraction are equal. Similar fractions are identically equal to 1 on the entire ODZ of the variables of this fraction:

5 5 = 1; - 2 3 - 2 3 = 1; x x = 1 ; - 3, 2 x 3 - 3, 2 x 3 = 1; 1 2 x - x 2 y 1 2 x - x 2 y ;

Since ordinary fractions are a special case of algebraic fractions, let us recall how they are reduced. The natural numbers written in the numerator and denominator are decomposed into prime factors, then the common factors are reduced (if any).

For example, 24 1260 = 2 2 2 3 2 2 3 3 5 7 = 2 3 5 7 = 2 105

The product of simple identical factors can be written as degrees, and in the process of fraction reduction, use the property of dividing degrees with the same bases. Then the above solution would be:

24 1260 = 2 3 3 2 2 3 2 5 7 = 2 3 - 2 3 2 - 1 5 7 = 2 105

(numerator and denominator divided by a common factor 2 2 3). Or, for clarity, based on the properties of multiplication and division, we will give the solution the following form:

24 1260 = 2 3 3 2 2 3 2 5 7 = 2 3 2 2 3 3 2 1 5 7 = 2 1 1 3 1 35 = 2 105

By analogy, the reduction of algebraic fractions is carried out, in which the numerator and denominator have monomials with integer coefficients.

Example 1

Given an algebraic fraction - 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z . It needs to be reduced.

Solution

It is possible to write the numerator and denominator of a given fraction as a product of prime factors and variables, and then reduce:

27 a 5 b 2 c z 6 a 2 b 2 c 7 z = - 3 3 3 a a a a a a b b c z 2 3 a a b b c c c c c c c c z = = - 3 3 a a a 2 c c c c c c c = - 9 a 3 2 c 6

However, a more rational way would be to write the solution as an expression with powers:

27 a 5 b 2 c z 6 a 2 b 2 c 7 z = - 3 3 a 5 b 2 c z 2 3 a 2 b 2 c 7 z = - 3 3 2 3 a 5 a 2 b 2 b 2 c c 7 z z = = - 3 3 - 1 2 a 5 - 2 1 1 1 c 7 - 1 1 = - 3 2 a 3 2 c 6 = - 9 a 3 2 c 6 .

Answer:- 27 a 5 b 2 c z 6 a 2 b 2 c 7 z = - 9 a 3 2 c 6

When there are fractional numerical coefficients in the numerator and denominator of an algebraic fraction, there are two possible ways of further actions: either separately divide these fractional coefficients, or first get rid of the fractional coefficients by multiplying the numerator and denominator by some natural number. The last transformation is carried out due to the main property of an algebraic fraction (you can read about it in the article “Reducing an algebraic fraction to a new denominator”).

Example 2

Given a fraction 2 5 x 0 , 3 x 3 . It needs to be reduced.

Solution

It is possible to reduce the fraction in this way:

2 5 x 0, 3 x 3 = 2 5 3 10 x x 3 = 4 3 1 x 2 = 4 3 x 2

Let's try to solve the problem differently, having previously got rid of fractional coefficients - we multiply the numerator and denominator by the least common multiple of the denominators of these coefficients, i.e. per LCM(5, 10) = 10. Then we get:

2 5 x 0, 3 x 3 = 10 2 5 x 10 0, 3 x 3 = 4 x 3 x 3 = 4 3 x 2.

Answer: 2 5 x 0, 3 x 3 = 4 3 x 2

When we reduce algebraic fractions general view, in which the numerators and denominators can be both monomials and polynomials, a problem is possible when the common factor is not always immediately visible. Or more than that, it simply doesn't exist. Then, to determine the common factor or fix the fact of its absence, the numerator and denominator of the algebraic fraction are factorized.

Example 3

Given a rational fraction 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 - 49 · b 3 . It needs to be shortened.

Solution

Let us factorize the polynomials in the numerator and denominator. Let's do the parentheses:

2 a 2 b 2 + 28 a b 2 + 98 b 2 a 2 b 3 - 49 b 3 = 2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49)

We see that the expression in brackets can be converted using the abbreviated multiplication formulas:

2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49) = 2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7)

It is clearly seen that it is possible to reduce the fraction by a common factor b 2 (a + 7). Let's make a reduction:

2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7) = 2 (a + 7) b (a - 7) = 2 a + 14 a b - 7 b

We write a short solution without explanation as a chain of equalities:

2 a 2 b 2 + 28 a b 2 + 98 b 2 a 2 b 3 - 49 b 3 = 2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49) = = 2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7) = 2 (a + 7) b (a - 7) = 2 a + 14 a b - 7 b

Answer: 2 a 2 b 2 + 28 a b 2 + 98 b 2 a 2 b 3 - 49 b 3 = 2 a + 14 a b - 7 b .

It happens that the common factors are hidden by numerical coefficients. Then, when reducing fractions, it is optimal to take out the numerical factors at higher powers of the numerator and denominator.

Example 4

Given an algebraic fraction 1 5 x - 2 7 x 3 y 5 x 2 y - 3 1 2 . It should be reduced if possible.

Solution

At first glance, the numerator and denominator do not have a common denominator. However, let's try to convert the given fraction. Let's take out the factor x in the numerator:

1 5 x - 2 7 x 3 y 5 x 2 y - 3 1 2 = x 1 5 - 2 7 x 2 y 5 x 2 y - 3 1 2

Now you can see some similarity between the expression in brackets and the expression in the denominator due to x 2 y . Let us take out the numerical coefficients at higher powers of these polynomials:

x 1 5 - 2 7 x 2 y 5 x 2 y - 3 1 2 = x - 2 7 - 7 2 1 5 + x 2 y 5 x 2 y - 1 5 3 1 2 = = - 2 7 x - 7 10 + x 2 y 5 x 2 y - 7 10

Now the common multiplier becomes visible, we carry out the reduction:

2 7 x - 7 10 + x 2 y 5 x 2 y - 7 10 = - 2 7 x 5 = - 2 35 x

Answer: 1 5 x - 2 7 x 3 y 5 x 2 y - 3 1 2 = - 2 35 x .

Let us emphasize that the skill of contraction rational fractions depends on the ability to factorize polynomials.

If you notice a mistake in the text, please highlight it and press Ctrl+Enter

Calculator online performs reduction of algebraic fractions in accordance with the fraction reduction rule: replacing the original fraction with an equal fraction, but with a smaller numerator and denominator, i.e. simultaneous division of the numerator and denominator of a fraction by their common greatest common divisor (GCD). The calculator also displays a detailed solution that will help you understand the sequence of the reduction.

Given:

Solution:

Doing Fraction Reduction

verification of the possibility of performing the reduction of an algebraic fraction

1) Determination of the greatest common divisor (GCD) of the numerator and denominator of a fraction

determination of the greatest common divisor (gcd) of the numerator and denominator of an algebraic fraction

2) Reducing the numerator and denominator of a fraction

reduction of the numerator and denominator of an algebraic fraction

3) Selection of the integer part of the fraction

extracting the integer part of an algebraic fraction

4) Converting an algebraic fraction to a decimal fraction

conversion of algebraic fraction to decimal

Help for the development of the site project

Dear site visitor.
If you could not find what you were looking for - be sure to write about it in the comments, what the site is missing now. This will help us understand in which direction we need to move further, and other visitors will soon be able to get the necessary material.
If the site turned out to be useful to you, donate the site to the project only 2 ₽ and we will know that we are moving in the right direction.

Thank you for not passing by!

I. The procedure for reducing an algebraic fraction with an online calculator:

1. To reduce an algebraic fraction, enter the values ​​of the numerator and denominator of the fraction in the appropriate fields. If the fraction is mixed, then also fill in the field corresponding to the integer part of the fraction. If the fraction is simple, then leave the integer part field blank.
2. To specify a negative fraction, put a minus sign in the integer part of the fraction.
3. Depending on the given algebraic fraction, the following sequence of actions is automatically performed:

• determining the greatest common divisor (GCD) of the numerator and denominator of a fraction;
• reduction of the numerator and denominator of a fraction by gcd;
• extracting the integer part of a fraction if the numerator of the final fraction is greater than the denominator.
• converting the final algebraic fraction to a decimal fraction rounded to hundredths.

II. For reference:

A fraction is a number consisting of one or more parts (fractions) of a unit. Common fraction(simple fraction) is written as two numbers (the numerator of the fraction and the denominator of the fraction) separated by a horizontal bar (fractional bar) denoting the sign of division. The numerator of a fraction is the number above the fraction bar. The numerator shows how many parts were taken from the whole. The denominator of a fraction is the number below the fractional bar. The denominator shows how many equal parts the whole is divided into. A simple fraction is a fraction that does not have an integer part. A simple fraction can be right or wrong. A proper fraction is a fraction whose numerator is less than the denominator, so a proper fraction is always less than one. Example of correct fractions: 8/7, 11/19, 16/17. An improper fraction is a fraction whose numerator is greater than or equal to the denominator, so an improper fraction is always greater than or equal to one. An example of improper fractions: 7/6, 8/7, 13/13. mixed fraction - a number that includes an integer and a proper fraction, and denotes the sum of this integer and a proper fraction. Any mixed fraction can be converted to an improper simple fraction. Example of mixed fractions: 1¼, 2½, 4¾.

III. Note:

1. The source data block is highlighted in yellow, block of intermediate calculations highlighted blue color , solution block highlighted in green.
2. For addition, subtraction, multiplication and division of ordinary or mixed fractions, use the online fraction calculator with a detailed solution.

So, we already know that the numerator and denominator of a fraction can be multiplied and divided by the same number, the fraction will not change from this. Consider three approaches:

First approach.

To reduce, divide the numerator and denominator by a common divisor. Consider examples:

Let's shorten:

In the above examples, we immediately see which divisors to take for reduction. The process is simple - we iterate over 2,3.4,5 and so on. In most examples of a school course, this is quite enough. But if there is a fraction:

Here the process with the selection of dividers can drag on for a long time;). Of course, such examples lie outside the school curriculum, but you need to be able to deal with them. Let's take a look at how this is done below. In the meantime, back to the reduction process.

As discussed above, in order to reduce the fraction, we carried out the division by the common divisor (s) we defined. Everything is correct! One has only to add signs of divisibility of numbers:

If the number is even then it is divisible by 2.

- if the number of the last two digits is divisible by 4, then the number itself is divisible by 4.

- if the sum of the digits that make up the number is divisible by 3, then the number itself is divisible by 3. For example, 125031, 1+2+5+0+3+1=12. Twelve is divisible by 3, so 123031 is divisible by 3.

- if the number ends with 5 or 0, then the number is divisible by 5.

- if the sum of the digits that make up the number is divisible by 9, then the number itself is divisible by 9. For example 625032 =.> 6+2+5+0+3+2=18. Eighteen is divisible by 9, so 623032 is divisible by 9.

Second approach.

In short, the essence, then in fact the whole action comes down to decomposing the numerator and denominator into factors and then reducing equal factors in the numerator and denominator (this approach is a consequence of the first approach):

Visually, in order not to get confused and not to make a mistake, equal multipliers are simply crossed out. The question is how to factorize a number? It is necessary to determine by enumeration all the divisors. This is a separate topic, it is simple, look at the information in a textbook or on the Internet. You will not encounter any great problems with the factorization of numbers that are present in the fractions of the school course.

Formally, the reduction principle can be written as follows:

Third approach.

Here is the most interesting for advanced and those who want to become one. Let's reduce the fraction 143/273. Try it yourself! Well, how quickly did it happen? And now look!

We turn it over (the numerator and denominator are interchanged). We divide the resulting fraction by a corner and translate it into mixed number, that is, we select the integer part:

Already easier. We see that the numerator and denominator can be reduced by 13:

And now do not forget to flip the fraction back again, let's write the whole chain:

Checked - it takes less time than searching and checking divisors. Let's go back to our two examples:

The first. We divide by a corner (not on a calculator), we get:

This fraction is simpler, of course, but there is again a problem with reduction. Now we separately analyze the fraction 1273/1463, turn it over:

It's already easier here. We can consider such a divisor as 19. The rest do not fit, it can be seen: 190:19= 10, 1273:19 = 67. Hooray! Let's write:

Next example. Let's cut 88179/2717.

We divide, we get:

Separately, we analyze the fraction 1235/2717, turn it over:

We can consider such a divisor as 13 (up to 13 are not suitable):

Numerator 247:13=19 Denominator 1235:13=95

*In the process, we saw another divisor equal to 19. It turns out that:

Now write down the original number:

And it doesn’t matter what will be more in the fraction - the numerator or the denominator, if the denominator, then we turn over and act as described. Thus, we can reduce any fraction, the third approach can be called universal.

Of course, the two examples discussed above are not simple examples. Let's try this technology on the "simple" fractions we have already considered:

Two fourths.

Seventy-two sixties. The numerator is greater than the denominator, no need to flip:

Of course, the third approach was applied to such simple examples just as an alternative. The method, as already mentioned, is universal, but not convenient and correct for all fractions, especially for simple ones.

The variety of fractions is great. It is important that you learn exactly the principles. Strict rule for working with fractions is simply not. We looked, figured out how it would be more convenient to act and move forward. With practice, the skill will come and you will click them like seeds.

Conclusion:

If you see a common divisor(s) for the numerator and denominator, then use them to reduce.

If you know how to quickly factorize a number, then decompose the numerator and denominator, then reduce.

If you can’t determine the common divisor in any way, then use the third approach.

*To reduce fractions, it is important to learn the principles of reduction, understand the basic property of a fraction, know the approaches to solving, and be extremely careful when calculating.

And remember! It is customary to reduce a fraction to the stop, that is, to reduce it while there is a common divisor.

Sincerely, Alexander Krutitskikh.