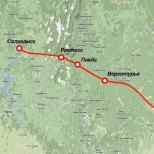
Punktis pideva funktsiooni kolm ekvivalentset definitsiooni. pidev funktsioon

Teoreem. Laske funktsioonil x=φ(t) punktis pidev a ja funktsioon y=f(x) punktis pidev b=φ(a). Siis kompleksfunktsioon y=f[φ(t)]=F(t) punktis pidev a.

Lase x=φ(t) ja y=f(x) on kõige lihtsamad elementaarfunktsioonid ja väärtuste kogum (x) funktsioonid x=φ(t) on funktsiooni ulatus y=f(x). Nagu me teame, on elementaarfunktsioonid pidevad ülesandeala igas punktis. Seetõttu on eelmise teoreemi kohaselt kompleksfunktsioon y=f(φ(t)), st kahe elementaarfunktsiooni superpositsioon on pidev. Näiteks on funktsioon pidev mis tahes punktis x ≠ 0, kahe elementaarfunktsiooni kompleksfunktsioonina x=t-1 ja y = sin x. Samuti funktsioon y=ln sin x pidev mis tahes intervalli punktis (2kπ,(2k+1)π), k ∈ Z (sinx>0).

1. Sissejuhatus.

2. Funktsiooni pidevuse definitsioon.

3. Katkestuste punktide klassifikatsioon

4. Pidevate funktsioonide omadused.

5. Järjepidevuse majanduslik tähendus.

6. Järeldus.

10.1. Sissejuhatus

Iga kord, hinnates meid ümbritseva maailma vältimatuid muutusi aja jooksul, püüame analüüsida käimasolevaid protsesse, et tuua esile nende olulisemad omadused. Üks esimesi küsimusi sellel teel on: kuidas ilmnevad sellele nähtusele iseloomulikud muutused - pidevalt või diskreetselt, st. spasmiliselt. Kas valuuta odavneb ühtlaselt või kukub kokku, kas toimub järkjärguline areng või revolutsiooniline hüpe? Kvalitatiivsete ja kvantitatiivsete hinnangute ühtlustamiseks toimuvale tuleks abstraheerida konkreetsest sisust ja uurida probleemi funktsionaalse sõltuvuse aspektist. See võimaldab meil teha piiride teooriat, mida käsitlesime viimases loengus.

10.2. Funktsiooni pidevuse määramine

Funktsiooni pidevus on intuitiivselt seotud tõsiasjaga, et selle graafik on pidev, mitte kuhugi katkev kõver. Joonistame sellise funktsiooni graafiku ilma pliiatsit paberilt tõstmata. Kui funktsioon on antud tabelis, siis selle järjepidevust rangelt võttes hinnata ei saa, kuna antud tabeli sammu puhul ei ole funktsiooni käitumine intervallides defineeritud.

Tegelikkuses toimub järjepidevusega järgmine asjaolu: kui olukorda iseloomustavad parameetrid natuke muuda siis natuke ka olukord muutub. Siin pole oluline mitte olukorra muutumine, vaid see, et see muutub "natuke".

Sõnastagem järjepidevuse mõiste juurdekasvu keeles. Mõnda nähtust kirjeldatakse funktsiooni ja punktiga a kuulub funktsiooni ulatusse. Erinevust nimetatakse argumentide juurdekasv punktis a, vahe on funktsiooni juurdekasv punktis a.

Definitsioon 10.1.Funktsioon punktis pidev a kui see on defineeritud selles punktis ja argumendi lõpmata väike juurdekasv vastab funktsiooni lõpmatu väikesele juurdekasvule:

Näide 10.1. Uurige funktsiooni pidevust punktis .

Lahendus. Koostame funktsiooni graafiku ja märgime sellele sammud D x ja D y(joonis 10.1).

Graafikult on näha, et mida väiksem on juurdekasv D x, seda vähem D y. Näitame seda analüütiliselt. Argumendi juurdekasv on , siis on funktsiooni juurdekasv selles punktis võrdne

See näitab, et kui , siis ja:

.

Anname veel ühe funktsiooni pidevuse definitsiooni.

Definitsioon 10.2.Funktsiooni kutsutakse pidev punktis a, kui:

1) see on määratletud punktis a ja mõnes selle naabruses;

2) ühepoolsed piirid on olemas ja on üksteisega võrdsed:

;

3) funktsiooni limiit punktis x® a on võrdne funktsiooni väärtusega selles punktis:

.

Kui vähemalt üks neist tingimustest on rikutud, siis väidetavalt läbib see funktsioon lõhe.

See määratlus töötab punktis järjepidevuse loomiseks. Järgides tema algoritmi ning märkides definitsiooni ja konkreetse näite nõuete kokkulangevusi ja lahknevusi, võime järeldada, et funktsioon on punktis pidev.

Definitsioon 2 näitab selgelt läheduse ideed, kui tutvustasime piiri mõistet. Argumendi piiramatu lähendusega x piirväärtusele a, pidev punktis a funktsiooni f(x) meelevaldselt piirväärtusele lähedale f(a).

10.3. Murdepunktide klassifikatsioon

Nimetatakse punkte, kus funktsiooni järjepidevuse tingimusi rikutakse murdepunktid seda funktsiooni. Kui a x 0 on funktsiooni katkestuspunkt, vähemalt üks funktsiooni pidevuse tingimus ei ole selles täidetud. Mõelge järgmisele näitele.

1. Funktsioon on määratletud punkti mõnes naabruses a, kuid pole punktis endas määratletud a. Näiteks ei ole funktsioon punktis määratletud a=2, mistõttu see läbib katkestuse (vt joonis 10.2).

Riis. 10.2 Joon. 10.3

2. Funktsioon on defineeritud punktis a ja mõnes selle naabruses on selle ühepoolsed piirid olemas, kuid need ei ole üksteisega võrdsed: , siis funktsioon läbib katkestuse. Näiteks funktsioon

on aga defineeritud punktis , kui funktsioonis esineb katkestus (vt joonis 10.3), kuna

ja ().

3. Funktsioon on defineeritud punktis a ja mõnes selle naabruses on funktsiooni piirang punktis , kuid see piir ei ole võrdne funktsiooni väärtusega punktis a:

.

Näiteks funktsioon (vt joonis 10.4)

Siin on murdepunkt:

,

Kõik katkestuspunktid on jagatud eemaldatavateks katkestuspunktideks, esimest ja teist tüüpi katkestuspunktideks.

Definitsioon 10.1. Murdepunkti nimetatakse punktiks parandatav vahe , kui selles punktis on vasakul ja paremal funktsiooni lõplikud piirid, mis on üksteisega võrdsed:

.

Funktsiooni piirang selles punktis on olemas, kuid ei ole võrdne funktsiooni väärtusega piirpunktis (kui funktsioon on piiripunktis defineeritud) või piirpunktis olev funktsioon ei ole määratletud.

Joonisel fig. 10.4 punktis rikutakse järjepidevuse tingimusi ja funktsioonil on katkestus. Punkt (0; 1) diagrammil välja torgatud. Seda lünka saab aga lihtsalt kõrvaldada – piisab etteantud funktsiooni uuesti defineerimisest, seades selle siinkohal võrdseks oma piiriga, s.t. pane . Seetõttu nimetatakse selliseid lünki eemaldatavateks.

Definitsioon 10.2. Murdepunkti nimetatakse 1. tüüpi katkestuspunkt , kui sellel hetkel on vasakul ja paremal funktsioonil lõplikud piirid, kuid need ei ole üksteisega võrdsed:

.

Sel hetkel öeldakse, et funktsioon kogeb hüpata.

Joonisel fig. 10.3 funktsioonil on punktis 1. tüüpi katkestus. Vasakul ja paremal olevad piirangud on selles punktis võrdsed:

ja .

Funktsiooni hüpe katkestuspunktis on võrdne .

Sellist funktsiooni on võimatu laiendada pidevaks. Graafik koosneb kahest hüppega eraldatud pooljoonest.

Definitsioon 10.3. Murdepunkti nimetatakse 2. tüüpi murdepunkt kui vähemalt ühte funktsiooni ühepoolsetest piiridest (vasak või parem) ei eksisteeri või see võrdub lõpmatusega.

Joonisel 10.3 on funktsioonil punktis teist tüüpi katkestus. Vaadeldav funktsioon at on lõpmatult suur ja sellel pole lõplikku piiri ei paremal ega vasakul. Seetõttu ei ole sellisel hetkel vaja rääkida järjepidevusest.

Näide 10.2. Koostage graafik ja määrake katkestuspunktide olemus:

Lahendus. Joonistame funktsiooni f(x) (Joonis 10.5).

Jooniselt on näha, et algsel funktsioonil on kolm murdepunkti: , x 2 = 1,
x 3 = 3. Arvestage neid järjekorras.

Seetõttu on punkt 2. tüüpi rebend.

a) Funktsioon on määratletud selles punktis: f(1) = –1.

b) , ,

need. punktis x 2 = 1 saadaval parandatav vahe. Alistades funktsiooni väärtuse selles punktis: f(1) = 5, katkestus kõrvaldatakse ja funktsioon muutub selles punktis pidevaks.

a) Funktsioon on määratletud selles punktis: f(3) = 1.

Nii et punktis x 1 = 3 saadaval 1. tüüpi rebend. Funktsioon kogeb sellel hetkel hüpet, mis on võrdne D-ga y= –2–1 = –3.

10.4. Pidevate funktsioonide omadused

Tuletades meelde piirväärtuste vastavaid omadusi, järeldame, et funktsioon, mis on samas punktis pidevate funktsioonide aritmeetiliste tehte tulemus, on samuti pidev. Märge:

1) kui funktsioonid ja on punktis pidevad a, siis funktsioonid , ja (tingimusel, et ) on ka selles punktis pidevad;

2) kui funktsioon on mingis punktis pidev a ja funktsioon on pidev punktis , siis liitfunktsioon on pidev punktis a ja

,

need. piirväärtuse märgi saab paigutada pideva funktsiooni märgi alla.

Nad ütlevad seda funktsioon on pidev mingis hulgas, kui see on pidev selle hulga igas punktis. Sellise funktsiooni graafik on pidev joon, mis tõmmatakse ühe pliiatsitõmbega läbi.

Kõik suuremad elementaarfunktsioonid on pidevad kõigis punktides, kus need on määratletud.

Funktsioonid, pidev segmendil, millel on mitmeid olulisi eristavaid omadusi. Sõnastame mõnda neist omadustest väljendavad teoreemid.

Teoreem 10.1 (Weierstrassi teoreem ). Kui funktsioon on segmendis pidev, saavutab see sellel lõigul oma minimaalse ja maksimaalse väärtuse.

Teoreem 10.2 (Cauchy teoreem ). Kui funktsioon on segmendil pidev, siis sellel lõigul on kõik vahepealsed väärtused väikseima ja suurima väärtuse vahel.

Cauchy teoreemist tuleneb järgmine oluline omadus.

Teoreem 10.3. Kui funktsioon on lõigul pidev ja võtab lõigu otstes erinevate märkide väärtused, siis a ja b vahel on punkt c, kus funktsioon kaob:.

Selle teoreemi geomeetriline tähendus on ilmne: kui pideva funktsiooni graafik läheb alumiselt pooltasandilt ülemisele (või vastupidi), siis vähemalt ühes punktis lõikub see teljega. Ox(joon.10.6).

Näide 10.3. Arvutage ligikaudu võrrandi juur

, (st ligikaudu asendada) vastava astme polünoom.

See pidevate funktsioonide omadus on praktika jaoks väga oluline. Näiteks on väga sageli pidevad funktsioonid antud tabelitega (vaatlus- või katseandmed). Seejärel saate mis tahes meetodil asendada tabelifunktsiooni polünoomiga. Vastavalt teoreemile 10.3 saab seda alati teha piisavalt suure täpsusega. Analüütiliselt etteantud funktsiooniga (eriti polünoomiga) töötamine on palju lihtsam.

10.5. Järjepidevuse majanduslik tähendus

Suurem osa majanduses kasutatavatest funktsioonidest on pidevad ja see võimaldab teha üsna olulisi majandusliku sisu väiteid.

Illustreerimiseks vaadake järgmist näidet.

maksumäär N sellel on joonisele fig sarnane graafik. 10.7a.

Lünkade otstes on see katkendlik ja need katkestused on esimest tüüpi. Küll aga tulumaksu summa P(joonis 10.7b) on aastasissetuleku pidev funktsioon K. Eelkõige sellest järeldub, et kui kahe inimese aastasissetulekud erinevad ebaoluliselt, siis peaks ka nende tasumisele kuuluva tulumaksu summa erinevus olema ebaoluline. Huvitav on see, et valdav enamus inimesi peab seda asjaolu täiesti loomulikuks, millele nad isegi ei mõtle.

10.6. Järeldus

Lõpetuseks teeme väikese kõrvalepõike.

Siin on, kuidas graafiliselt väljendada iidsete inimeste kurba tähelepanekut:

Sic transit Gloria mundi …

(Nii möödub maise auhiilgus …)

Töö lõpp -

See teema kuulub:

Funktsiooni kontseptsioon

Funktsiooni mõiste.. kõik voolab ja kõik muutub Herakleitos.. tabel x x x x y y y y y y y y y

Kui vajate sellel teemal lisamaterjali või te ei leidnud seda, mida otsisite, soovitame kasutada otsingut meie tööde andmebaasis:

Mida me teeme saadud materjaliga:

Kui see materjal osutus teile kasulikuks, saate selle sotsiaalvõrgustikes oma lehele salvestada:

Definitsioon
funktsioon f (x) helistas pidev punktis x 0 selle punkti naabruses ja kui piir kui x kaldub x-le 0 võrdub funktsiooni väärtusega punktis x 0 :
.

Kasutades funktsiooni piiri Cauchy ja Heine definitsioone, saab anda funktsiooni pidevuse üksikasjalikud määratlused punktis .

Järjepidevuse mõiste võib sõnastada juurdekasvu tingimused. Selleks võtame kasutusele uue muutuja, mida nimetatakse muutuja x juurdekasvuks punktis. Siis on funktsioon pidev punktis if
.
Tutvustame uut funktsiooni:
.
Nad kutsuvad teda funktsiooni juurdekasv punktis . Siis on funktsioon pidev punktis if
.

Järjepidevuse määratlus paremal (vasakul)
funktsioon f (x) helistas pidev paremal (vasakul) punktis x 0 , kui see on määratletud selle punkti mõnes parempoolses (vasakukäelises) naabruses ja kui parem (vasak) piir punktis x 0 võrdub funktsiooni väärtusega punktis x 0 :
.

Piiritusteoreem pideva funktsiooni jaoks
Olgu funktsioon f (x) pidev punktis x 0 . Siis on olemas naabruskond U (x0) mille funktsioon on piiratud.

Teoreem pideva funktsiooni märgi säilimise kohta
Olgu funktsioon pidev punktis . Ja olgu sel hetkel positiivne (negatiivne) väärtus:
.
Siis on selline punkti naabrus, kus funktsioonil on positiivne (negatiivne) väärtus:
aadressil .

Pidevate funktsioonide aritmeetilised omadused
Olgu funktsioonid ja pidevad punktis .
Siis funktsioonid ja on pidevad punktis .
Kui , siis on funktsioon pidev ka punktis .

Vasak ja parem järjepidevuse omadus
Funktsioon on pidev punktis siis ja ainult siis, kui see on pidev paremal ja vasakul.

Omaduste tõestused on toodud lehel "Punktis pidevate funktsioonide omadused".

Kompleksfunktsiooni järjepidevus

Kompleksfunktsiooni pidevuse teoreem
Olgu funktsioon pidev punktis . Ja olgu funktsioon pidev punktis .
Siis on kompleksfunktsioon pidev punktis .

Kompleksfunktsiooni piirang

Teoreem funktsiooni pidevfunktsiooni piiri kohta
Olgu funktsiooni limiit , ja see on võrdne:
.
Siin punkt t 0 võib olla lõplik või lõpmatus: .
Ja olgu funktsioon pidev punktis .
Siis on kompleksfunktsiooni piirang ja see on võrdne:
.

Kompleksfunktsiooni piirteoreem
Laske funktsioonil olla piir ja kaardistada punkti punkteeritud naabruskond punkti punkteeritud ümbrusega. Olgu see funktsioon sellel naabruskonnal määratletud ja sellel on piirang.
Siin - lõplikud või lõpmata kauged punktid: . Naabruskonnad ja neile vastavad piirid võivad olla kas kahe- või ühepoolsed.
Siis on kompleksfunktsiooni piirang ja see on võrdne:
.

murdepunktid

Murdepunkti määramine
Olgu funktsioon defineeritud punkti mõnel punkteeritud naabruskonnal. Punkti nimetatakse funktsiooni katkestuspunkt kui üks kahest tingimusest on täidetud:
1) ei ole määratletud ;
2) on määratletud kohas , kuid ei ole selles punktis.

1. tüüpi murdepunkti määramine
Punkti nimetatakse esimest tüüpi murdepunkt, kui on murdepunkt ja vasakul ja paremal on lõplikud ühepoolsed piirangud:
.

Funktsiooni hüppe määratlus
Hüppa Δ funktsioon punktis nimetatakse erinevust paremal ja vasakul pool olevate piiride vahel
.

Katkestuspunkti määramine
Punkti nimetatakse murdepunkt kui on piir
,
kuid funktsioon punktis ei ole kas defineeritud või ei ole võrdne piirväärtusega: .

Seega on katkestuspunkt 1. tüüpi katkestuspunkt, mille juures funktsiooni hüpe võrdub nulliga.

2. tüüpi murdepunkti määramine
Punkti nimetatakse teist tüüpi murdepunkt, kui see ei ole 1. tüüpi katkestuspunkt. See tähendab, et kui punktis ei ole vähemalt ühte ühepoolset piiri või vähemalt üks ühepoolne piir on võrdne lõpmatusega.

Intervallil pidevate funktsioonide omadused

Lõigul pideva funktsiooni definitsioon
Funktsiooni nimetatakse pidevaks lõigul (at ), kui see on pidev avatud intervalli kõikides punktides (at ) ning punktides a ja b .

Weierstrassi esimene teoreem intervallil pideva funktsiooni piirituse kohta
Kui funktsioon on lõigul pidev, siis on see selle lõiguga piiratud.

Maksimumi (miinimum) saavutatavuse määramine
Funktsioon saavutab hulgal oma maksimumi (miinimum), kui selle jaoks on argument
kõigi jaoks .

Ülemise (alumise) piiri saavutatavuse määramine
Funktsioon saavutab hulga ülemise (alumise) piiri, kui selle jaoks on argument
.

Weierstrassi teine ​​teoreem pideva funktsiooni maksimumi ja miinimumi kohta
Lõigul pidev funktsioon saavutab sellel oma ülemise ja alumise piiri või, mis on sama asi, saavutab lõigul oma maksimumi ja miinimumi.

Bolzano-Cauchy vaheväärtuste teoreem
Olgu funktsioon pidev intervallil . Ja olgu C suvaline arv segmendi otstes oleva funktsiooni väärtuste vahel: ja . Siis on punkt, mille jaoks
.

Järeldus 1
Olgu funktsioon pidev intervallil . Ja laske funktsiooni väärtustel segmendi otstes olla erinevad märgid: või . Siis on punkt, kus funktsiooni väärtus on võrdne nulliga:
.

Tagajärg 2
Olgu funktsioon pidev intervallil . Lase sel minna . Seejärel võtab funktsioon segmenti kõik väärtused ja ainult need väärtused:
aadressil .

Pöördfunktsioonid

Pöördfunktsiooni definitsioon
Olgu funktsioonil domeen X ja väärtuste komplekt Y . Ja las tal on vara:
kõigi jaoks .
Siis saab hulga Y mis tahes elemendi jaoks seostada ainult ühe hulga X elemendi, mille jaoks . See vastavus määratleb funktsiooni nimega pöördfunktsioon kuni . Pöördfunktsioon on tähistatud järgmiselt:
.

Definitsioonist tuleneb, et
;
kõigi jaoks ;
kõigi jaoks .

Lemma otse- ja pöördfunktsioonide vastastikuse monotoonsuse kohta
Kui funktsioon on rangelt kasvav (kahanev), siis on olemas pöördfunktsioon, mis on samuti rangelt kasvav (kahanev).

Omadus otse- ja pöördfunktsioonide graafikute sümmeetria kohta
Otsese ja pöördfunktsiooni graafikud on otsejoone suhtes sümmeetrilised.

Teoreem pöördfunktsiooni olemasolu ja pidevuse kohta segmendil
Olgu funktsioon pidev ja rangelt kasvav (kahanev) intervallil . Seejärel on intervallil defineeritud ja pidev pöördfunktsioon, mis on rangelt kasvav (kahanev).

Funktsiooni suurendamiseks. Laskumiseks - .

Teoreem pöördfunktsiooni olemasolu ja pidevuse kohta intervallil
Olgu funktsioon pidev ja rangelt kasvav (kahanev) avatud lõplikul või lõpmatul intervallil. Seejärel määratletakse pöördfunktsioon ja see on pidev intervallil, mis on rangelt suurenev (kahanev).

Funktsiooni suurendamiseks.
Laskumiseks: .

Sarnaselt saab sõnastada teoreemi pöördfunktsiooni olemasolu ja pidevuse kohta poolintervallil.

Elementaarfunktsioonide omadused ja järjepidevus

Elementaarfunktsioonid ja nende pöördväärtused on oma määratlusvaldkonnas pidevad. Järgnevalt anname vastavate teoreemide formuleeringud ja viitame nende tõestustele.

Eksponentfunktsioon

eksponentsiaalfunktsioon f (x) = x, alusega a > 0 on jada piir
,
kus on suvaline ratsionaalarvude jada, mis kaldub x-le:
.

Teoreem. Eksponentfunktsiooni omadused
Eksponentfunktsioonil on järgmised omadused:
(P.0) on määratletud jaoks , kõigile ;
(lk 1) kui a ≠ 1 sellel on palju tähendusi;
(lk 2) rangelt suureneb , rangelt väheneb juures , on konstantne juures ;
(lk 3) ;
(lk 3*) ;
(lk 4) ;
(lk 5) ;
(lk 6) ;
(lk 7) ;
(lk 8) on kõigi jaoks pidev;
(lk 9) kell ;
aadressil .

Logaritm

Logaritmiline funktsioon ehk logaritm, y = log x, alusega a on eksponentsiaalfunktsiooni pöördväärtus alusega a.

Teoreem. Logaritmi omadused
Logaritmiline funktsioon alusega a, y = logi x, sellel on järgmised omadused:
(L.1) on defineeritud ja pidev, argumendi positiivsete väärtuste jaoks ja ,;
(L.2) sellel on palju tähendusi;
(L.3) rangelt suureneb juures , rangelt väheneb juures ;
(L.4) kell ;
kell ;
(L.5) ;
(L.6) kell ;
(L.7) kell ;
(L.8) kell ;
(L.9) aadressil .

Eksponent ja naturaallogaritm

Eksponentfunktsiooni ja logaritmi definitsioonides esineb konstant a, mida nimetatakse astme baasiks või logaritmi baasiks. Matemaatilises analüüsis saadakse enamikul juhtudel lihtsamad arvutused, kui aluseks võtta arv e:
.
Eksponentfunktsiooni, mille alus on e, nimetatakse eksponendiks: , ja aluse e logaritmi nimetatakse naturaallogaritmiks: .

Eksponendi omadused ja naturaallogaritm on toodud lehekülgedel
"Exponent, e x astmele",
"looduslik logaritm, funktsioon ln x"

Toitefunktsioon

Astmefunktsioon koos eksponendiga p on funktsioon f (x) = xp, mille väärtus punktis x on võrdne eksponentsiaalfunktsiooni väärtusega alusega x punktis p .
Lisaks on f (0) = 0 p = 0 p > jaoks 0 .

Siin käsitleme võimsusfunktsiooni y = x p omadusi argumendi mittenegatiivsete väärtuste jaoks. Ratsionaal- ja paaritu m puhul on eksponentsiaalfunktsioon defineeritud negatiivse x jaoks. Sel juhul saab selle omadused saada paaris või paaritu abil.
Neid juhtumeid käsitletakse ja illustreeritakse üksikasjalikult lehel Toitefunktsioon, selle omadused ja graafikud.

Teoreem. Toitefunktsiooni omadused (x ≥ 0)
Astmefunktsioonil y = x p eksponendiga p on järgmised omadused:
(C.1) võtteplatsil määratletud ja pidev
kell ,
aadressil ".

Trigonomeetrilised funktsioonid

Trigonomeetriliste funktsioonide pidevuse teoreem
Trigonomeetrilised funktsioonid: siinus ( sin x), koosinus ( cos x), puutuja ( tg x) ja kotangent ( ctg x

Pöördtrigonomeetriliste funktsioonide pidevuse teoreem
Trigonomeetrilised pöördfunktsioonid: arcsiinus ( arcsin x), kaarekoosinus ( arccos x), kaartangens ( arctg x) ja kaartangens ( arcctg x) on oma määratlusvaldkondades pidevad.

Viited:
O.I. Deemonid. Loengud matemaatilisest analüüsist. 1. osa. Moskva, 2004.
L.D. Kudrjavtsev. Matemaatilise analüüsi kursus. 1. köide. Moskva, 2003.
CM. Nikolski. Matemaatilise analüüsi kursus. 1. köide. Moskva, 1983.

Vaatleme kahte funktsiooni, mille graafikud on näidatud joonisel fig. 1 ja 2. Esimese funktsiooni graafiku saab joonistada ilma pliiatsit paberilt tõstmata. Seda funktsiooni võib nimetada pidevaks. Sel viisil on võimatu joonistada teise funktsiooni graafikut. See koosneb kahest pidevast tükist ja teatud punktis on sellel katkestus ja me nimetame funktsiooni katkendlikuks.

Selline visuaalne järjepidevuse määratlus ei saa kuidagi matemaatikaga sobida, kuna see sisaldab täiesti mittematemaatilisi mõisteid "pliiats" ja "paber". Järjepidevuse täpne matemaatiline definitsioon on antud piiri mõiste alusel ja koosneb järgnevast.

Olgu funktsioon defineeritud segmendil ja olla selle segmendi mingi punkt. Funktsiooni nimetatakse pidevaks punktis, kui, nagu see kipub (seda peetakse ainult segmendist), kipuvad funktsiooni väärtused, s.o. kui

. (1)

Funktsiooni nimetatakse pidevaks lõigul, kui see on pidev selle igas punktis.

Kui võrdsus (1) ei ole punktis täidetud, nimetatakse funktsiooni punktis katkendlikuks.

Nagu näeme, määratakse matemaatiliselt funktsiooni pidevuse omadus segmendil punktis pidevuse lokaalse (lokaalse) omaduse kaudu.

Väärtust nimetatakse argumendi juurdekasvuks, funktsiooni väärtuste erinevust nimetatakse funktsiooni juurdekasvuks ja seda tähistatakse . Ilmselgelt kaldub argumendi juurdekasvu poole kaldudes nulli: .

Kirjutame võrdsuse (1) ümber samaväärsel kujul

.

Kasutades kasutusele võetud tähistust, saab selle ümber kirjutada järgmiselt:

Seega, kui funktsioon on pidev, siis kui argumendi juurdekasv kaldub nulli, kipub funktsiooni juurdekasv olema null. Nad ütlevad teisiti: argumendi väike juurdekasv vastab funktsiooni väikesele juurdekasvule. Joonisel fig. 3 on kujutatud punktis pideva funktsiooni graafik, juurdekasv vastab funktsiooni juurdekasvule. Joonisel fig. 4 juurdekasv vastab funktsiooni sellisele juurdekasvule, mis olenemata sellest, kui väike on, ei ole väiksem kui pool lõigu pikkusest; funktsioon on punktis katkendlik.

Meie ettekujutust pidevast funktsioonist kui funktsioonist, mille graafikut saab joonistada ilma pliiatsit paberilt tõstmata, toetavad suurepäraselt pidevate funktsioonide omadused, mis on tõestatud arvutustes. Märgime näiteks nende omadused.

1. Kui pidev funktsioon lõigul võtab lõigu otstes erinevate märkide väärtused, siis selle lõigu mingil hetkel omandab see väärtuse, mis on võrdne nulliga.

2. Funktsioon , mis jätkub lõigul , võtab kõik vaheväärtused lõpp-punktide väärtuste vahel, st. ja vahel.

3. Kui funktsioon on lõigul pidev, siis sellel lõigul saavutab ta oma maksimumi ja oma miinimumväärtused, s.o. kui - funktsiooni väikseim ja - suurimad väärtused segmendil , siis sellel segmendil on punkte ja , nii et ja .

Neist esimese väite geomeetriline tähendus on üsna selge: kui pidev kõver kulgeb telje ühelt küljelt teisele, siis see lõikub selle teljega (joonis 5). Katkendlikul funktsioonil seda omadust ei ole, mida kinnitab funktsiooni graafik joonisel fig. 2, samuti omadused 2 ja 3. Joonisel fig. Funktsioon 2 ei võta väärtust , kuigi see on ja vahel. Joonisel fig. 6 on näide katkendlikust funktsioonist (arvu murdosast), mis ei saavuta maksimaalset väärtust.

Samal lõigul olevate pidevate funktsioonide liitmine, lahutamine, korrutamine viivad taas pidevate funktsioonideni. Kahe pideva funktsiooni jagamisel saadakse pidev funktsioon, kui nimetaja on kõikjal nullist erinev.

Matemaatika jõudis pideva funktsiooni mõisteni, uurides ennekõike erinevaid liikumisseadusi. Ruum ja aeg on pidevad ning näiteks teekonna seadusega väljendatud sõltuvus ajast annab näite pidevast funktsioonist.

Pidevad funktsioonid kirjeldavad tahkete ainete, vedelike ja gaaside olekuid ja protsesse. Neid uurivaid teadusi - elastsuse teooriat, hüdrodünaamikat ja aerodünaamikat - ühendab üks nimi - "kontiinummehaanika".

Selles õppetükis õpime, kuidas määrata funktsiooni järjepidevust. Teeme seda piirangute abil, pealegi ühekülgselt - parem- ja vasakpoolne, mis pole sugugi hirmutav, hoolimata sellest, et need on kirjutatud kujul ja .

Mis on aga funktsiooni järjepidevus üldiselt? Kuni jõuame range määratluseni, on kõige lihtsam viis ette kujutada joont, mille saab tõmmata ilma pliiatsit paberilt tõstmata. Kui selline joon tõmmata, siis on see pidev. See joon on pideva funktsiooni graafik.

Graafiliselt on funktsioon mingis punktis pidev, kui selle graafik selles punktis ei "murdu". Sellise pideva funktsiooni graafik on näidatud alloleval joonisel.

Funktsiooni pidevuse definitsioon läbi piiri. Funktsioon on punktis pidev kolmel tingimusel:

1. Funktsioon on defineeritud punktis .

Kui vähemalt üks ülaltoodud tingimustest ei ole täidetud, ei ole funktsioon punktis pidev. Samal ajal öeldakse, et funktsioon kannatab katkestuse all ja graafiku punkte, kus graafik katkestatakse, nimetatakse funktsiooni katkestuspunktideks. Sellise punktis x=2 katkeva funktsiooni graafik on näidatud alloleval joonisel.

Näide 1 Funktsioon f(x) on määratletud järgmiselt:

Kas see funktsioon on pidev igas oma haru piiripunktis, st punktides x = 0 , x = 1 , x = 3 ?

Lahendus. Kontrollime kõiki kolme funktsiooni järjepidevuse tingimust igas piiripunktis. Esimene tingimus on täidetud, sest funktsioon määratletud igas piiripunktis tuleneb funktsiooni definitsioonist. Jääb üle kontrollida ülejäänud kaks tingimust.

Punkt x= 0. Leidke sellest punktist vasakpoolne piir:

.

Leiame parempoolse piirangu:

x= 0 tuleb leida seda punkti sisaldava funktsiooni harust, st teisest harust. Leiame need:

Nagu näete, funktsiooni piir ja funktsiooni väärtus punktis x= 0 on võrdsed. Seetõttu on funktsioon punktis pidev x = 0 .

Punkt x= 1. Leidke sellest punktist vasakpoolne piir:

Leiame parempoolse piirangu:

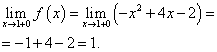
Funktsiooni piirang ja funktsiooni väärtus punktis x= 1 tuleb leida seda punkti sisaldava funktsiooni harust, st teisest harust. Leiame need:

.

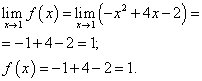Funktsiooni piirang ja funktsiooni väärtus punktis x= 1 on võrdsed. Seetõttu on funktsioon punktis pidev x = 1 .

Punkt x= 3. Leidke sellest punktist vasakpoolne piir:

Leiame parempoolse piirangu:

Funktsiooni piirang ja funktsiooni väärtus punktis x= 3 tuleb leida seda punkti sisaldava funktsiooni harust, st teisest harust. Leiame need:

.

Funktsiooni piirang ja funktsiooni väärtus punktis x= 3 on võrdsed. Seetõttu on funktsioon punktis pidev x = 3 .

Peamine järeldus: see funktsioon on pidev igas piiripunktis.

Looge ise funktsiooni järjepidevus mingis punktis ja seejärel vaadake lahendust

Funktsiooni pidevat muutust saab defineerida kui järkjärgulist, ilma hüpeteta muutust, mille puhul argumendi väike muutus toob kaasa funktsiooni väikese muutuse.

Illustreerime seda funktsiooni pidevat muutumist näitega.

Laske koormal laua kohal niidil rippuda. Selle koormuse mõjul on niit venitatud, nii et vahemaa l koormus keerme riputuspunktist on funktsioon koormuse massist m, see on l = f(m) , m≥0 .

Kui muudame veidi koorma massi, siis vahemaad l vähe muutust: vähe muutust m vastavad väikestele muudatustele l. Kui aga koormuse mass on lähedane keerme tõmbetugevusele, võib koormuse massi väike suurenemine põhjustada keerme purunemise: kaugus l suureneb järsult ja võrdub kaugusega ripppunktist lauapinnani. Funktsioonigraafik l = f(m) näidatud joonisel. Saidil on see graafik pidev (pidev) joon ja punktis, kus see katkeb. Tulemuseks on kahest harust koosnev graafik. Kõigis punktides, välja arvatud funktsioon l = f(m) on pidev ja teatud punktis on sellel katkestus.

Funktsiooni järjepidevuse uurimine võib olla nii iseseisev ülesanne kui ka funktsiooni täieliku uurimise ja selle graafiku koostamise üks etappidest.

Funktsiooni pidevus intervallil

Laske funktsioonil y = f(x) määratletud intervallis ] a, b[ ja on pidev selle intervalli igas punktis. Siis nimetatakse seda intervallis pidevaks ] a, b[ . Funktsiooni pidevuse mõiste vormi ]-∞ intervallidel on defineeritud sarnaselt, b[ , ]a, + ∞[ , ]- ∞, + ∞[ . Nüüd lase funktsioon y = f(x) määratletud segmendil [ a, b] . Intervalli ja lõigu erinevus seisneb selles, et intervalli piiripunktid ei kuulu intervalli, kuid lõigu piiripunktid on lõigusse kaasatud. Siin tuleks mainida nn ühekülgset järjepidevust: punktis a, jäädes intervallile [ a, b] , saame läheneda ainult paremalt ja punktini b- ainult vasakul. Funktsiooni nimetatakse pidevaks lõigul [ a, b] , kui see on pidev selle lõigu kõigis sisepunktides, pidev punktis paremal a ja jäetakse punktis pidevaks b.

Iga elementaarfunktsioon võib olla pideva funktsiooni näide. Iga elementaarfunktsioon on pidev mis tahes segmendis, millel see on määratletud. Näiteks funktsioonid ja on pidevad mis tahes intervalli [ a, b], funktsioon on pidev intervallil [ 0 , b] , on funktsioon pidev igal lõigul, mis ei sisalda punkti a = 2 .

Näide 4 Uurige järjepidevuse funktsiooni.

Lahendus. Kontrollime esimest tingimust. Funktsioon ei ole punktides 3 ja 3 määratletud. Vähemalt üks funktsiooni järjepidevuse tingimus tervel arvureal ei ole täidetud. Seetõttu on see funktsioon intervallidel pidev

Näide 5 Määrake, millisel parameetri väärtusel a pidev kogu ulatuses domeenid funktsiooni

Lahendus.

Leiame parempoolse piirangu:

.

On ilmne, et väärtus punktis x= 2 peab olema võrdne kirves :

a = 1,5 .

Näide 6 Määrake, millistel parameetrite väärtustel a ja b pidev kogu ulatuses domeenid funktsiooni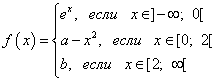

Lahendus.
Leia funktsiooni vasakpoolne piir punktis :

.

Seetõttu peab punkti väärtus olema võrdne 1-ga:

Leiame vasakpoolse funktsiooni punktist:

Ilmselt peaks funktsiooni väärtus punktis olema võrdne:

Vastus: funktsioon on pidev kogu definitsioonipiirkonna ulatuses a = 1; b = -3 .

Pidevate funktsioonide põhiomadused

Matemaatika jõudis pideva funktsiooni mõisteni, uurides ennekõike erinevaid liikumisseadusi. Ruum ja aeg on lõputud ning sõltuvused nagu teed s ajast t, mida väljendab seadus s = f(t) , toob näite pidevast funktsioonid f(t) . Ka soojendatava vee temperatuur muutub pidevalt, see on ka aja pidev funktsioon: T = f(t) .

Matemaatilises analüüsis on tõestatud mõned omadused, et pidevad funktsioonid on. Tutvustame neist omadustest kõige olulisemat.

1. Kui funktsioon, mis on intervallil pidev, omandab intervalli otstes erinevate märkide väärtused, siis selle segmendi mingis punktis omandab see väärtuse, mis on võrdne nulliga. Formaalsemalt on see omadus antud teoreemis, mida tuntakse esimese Bolzano-Cauchy teoreemina.

2. Funktsioon f(x) pidev intervallil [ a, b], võtab kõik vahepealsed väärtused lõpp-punktide väärtuste vahel, st vahel f(a) ja f(b) . Formaalsemalt on see omadus antud teoreemis, mida tuntakse teise Bolzano-Cauchy teoreemina.