Korrutage lihtmurrud. Murdude korrutamine ja jagamine

Murru murdosa või murdosa arvuga korrektseks korrutamiseks peate teadma lihtsad reeglid. Nüüd analüüsime neid reegleid üksikasjalikult.

Hariliku murru korrutamine murdosaga.

Murru korrutamiseks murdosaga peate arvutama nende murdude lugejate ja nimetajate korrutise.

\(\bf \frac(a)(b) \times \frac(c)(d) = \frac(a \times c)(b \times d)\\\)

Vaatame näidet:
Korrutame esimese murru lugeja teise murru lugejaga ja korrutame ka esimese murru nimetaja teise murru nimetajaga.

\(\frac(6)(7) \times \frac(2)(3) = \frac(6 \times 2)(7 \times 3) = \frac(12)(21) = \frac(4 \ korda 3) (7 \ korda 3) = \frac(4) (7)\\\)

Murd \(\frac(12)(21) = \frac(4 \times 3)(7 \times 3) = \frac(4)(7)\\\) vähendati 3 võrra.

Murru korrutamine arvuga.

Kõigepealt tuletagem meelde reeglit, mis tahes arvu saab esitada murdena \(\bf n = \frac(n)(1)\) .

Kasutame seda reeglit korrutamisel.

\(5 \ korda \ frac (4) (7) = \ frac (5) (1) \ korda \ frac (4) (7) = \ frac (5 \ korda 4) (1 \ korda 7) = \ frac (20) (7) = 2\frac(6) (7)\\\)

Vale murd \(\frac(20)(7) = \frac(14 + 6)(7) = \frac(14)(7) + \frac(6)(7) = 2 + \frac(6)( 7)= 2\frac(6)(7)\\\) teisendatuna segamurruks.

Teisisõnu, Arvu korrutamisel murdosaga korrutame arvu lugejaga ja nimetaja jätame muutmata. Näide:

\(\frac(2)(5) \times 3 = \frac(2 \times 3)(5) = \frac(6)(5) = 1\frac(1)(5)\\\\\) \(\bf \frac(a)(b) \times c = \frac(a \times c)(b)\\\)

Segamurdude korrutamine.

Segamurdude korrutamiseks peate esmalt esitama iga segamurru valemurruna ja seejärel kasutama korrutamisreeglit. Korrutame lugeja lugejaga ja nimetaja nimetajaga.

Näide:
\(2\frac(1)(4) \times 3\frac(5)(6) = \frac(9)(4) \times \frac(23)(6) = \frac(9 \times 23) (4 \ korda 6) = \frac(3 \ korda \värv(punane) (3) \ korda 23) (4 \ korda 2 \ korda \värv(punane) (3)) = \frac(69) (8) = 8\frac(5)(8)\\\)

Vastastikuste murdude ja arvude korrutamine.

Murd \(\bf \frac(a)(b)\) on murdosa \(\bf \frac(b)(a)\ pöördväärtus, tingimusel et a≠0,b≠0.
Murrud \(\bf \frac(a)(b)\) ja \(\bf \frac(b)(a)\) nimetatakse vastastikusteks murdudeks. Vastastikuste murdude korrutis on 1.
\(\bf \frac(a)(b) \times \frac(b)(a) = 1 \\\)

Näide:
\(\frac(5)(9) \times \frac(9)(5) = \frac(45)(45) = 1\\\)

Seotud küsimused:
Kuidas korrutada murdosa murdosaga?
Vastus: Harilike murdude korrutis on lugeja korrutamine lugejaga, nimetaja nimetajaga. Segafraktsioonide korrutise saamiseks peate need teisendama valeks fraktsiooniks ja korrutama vastavalt reeglitele.

Kuidas korrutada erinevate nimetajatega murde?
Vastus: pole vahet, kas need on samad või erinevad nimetajad Murdude puhul toimub korrutamine vastavalt reeglile, mille kohaselt leitakse lugeja korrutis lugejaga, nimetaja nimetajaga.

Kuidas segatud murde korrutada?
Vastus: kõigepealt peate segamurru teisendama valeks murruks ja seejärel leidma korrutise korrutamisreeglite järgi.

Kuidas korrutada arvu murdosaga?
Vastus: korrutame arvu lugejaga, kuid nimetaja jätame samaks.

Näide nr 1:
Arvutage korrutis: a) \(\frac(8)(9) \times \frac(7) (11)\) b) \(\frac(2) (15) \times \frac(10) (13) \ )

Lahendus:
a) \(\frac(8)(9) \times \frac(7)(11) = \frac(8 \times 7)(9 \times 11) = \frac(56)(99)\\\\ \)
b) \(\frac(2)(15) \times \frac(10)(13) = \frac(2 \times 10)(15 \times 13) = \frac(2 \ korda 2 \ korda \värv( punane) (5)) (3 \ korda \värv (punane) (5) \ korda 13) = \frac(4) (39)\)

Näide nr 2:
Arvutage arvu ja murru korrutised: a) \(3 \times \frac(17) (23)\) b) \(\frac(2) (3) \times 11\)

Lahendus:
a) \(3 \ korda \ frac (17) (23) = \ frac (3) (1) \ korda \ frac (17) (23) = \ frac (3 \ korda 17) (1 \ korda 23) = \frac(51)(23) = 2\frac(5)(23)\\\\\)
b) \(\frac(2)(3) \times 11 = \frac(2)(3) \times \frac(11)(1) = \frac(2 \times 11) (3 \times 1) = \frac(22)(3) = 7\frac(1)(3)\)

Näide nr 3:
Kirjutage murru \(\frac(1)(3)\) pöördväärtus?
Vastus: \(\frac(3)(1) = 3\)

Näide nr 4:
Arvutage kahe vastastikku pöördmurru korrutis: a) \(\frac(104)(215) \times \frac(215)(104)\)

Lahendus:
a) \(\frac(104)(215) \times \frac(215)(104) = 1\)

Näide nr 5:
Kas pöördmurrud võivad olla:
a) samaaegselt õigete murdudega;
b) samaaegselt valemurrud;
c) samaaegselt naturaalarvud?

Lahendus:
a) esimesele küsimusele vastamiseks toome näite. Murd \(\frac(2)(3)\) on õige, selle pöördmurd on võrdne \(\frac(3)(2)\) - vale murd. Vastus: ei.

b) peaaegu kõigi murdude puhul ei ole see tingimus täidetud, kuid on mõned arvud, mis vastavad tingimusele, et ei ole samal ajal õige murdosa. Näiteks vale murd on \(\frac(3)(3)\), selle pöördmurd on võrdne \(\frac(3)(3)\). Saame kaks vale murdu. Vastus: mitte alati teatud tingimustel, kui lugeja ja nimetaja on võrdsed.

c) naturaalarvud on arvud, mida kasutame loendamisel, näiteks 1, 2, 3, …. Kui võtame arvu \(3 = \frac(3)(1)\), siis on selle pöördmurruks \(\frac(1)(3)\). Murd \(\frac(1)(3)\) ei ole naturaalarv. Kui me käime läbi kõik arvud, on arvu pöördarvuks alati murd, välja arvatud 1. Kui võtame arvu 1, siis selle pöördmurd on \(\frac(1)(1) = \frac(1 )(1) = 1\). Number 1 naturaalarv. Vastus: need võivad korraga olla naturaalarvud ainult ühel juhul, kui see on arv 1.

Näide nr 6:
Tehke segamurdude korrutis: a) \(4 korda 2\frac(4) (5)\) b) \(1\frac(1) (4) \ korda 3\frac(2) (7)\ )

Lahendus:
a) \(4 korda 2\frac(4)(5) = \frac(4)(1) \ korda \frac(14)(5) = \frac(56)(5) = 11\frac(1) )(5)\\\\ \)
b) \(1\frac(1)(4) \times 3\frac(2)(7) = \frac(5)(4) \times \frac(23)(7) = \frac(115)( 28) = 4\frac(3)(7)\)

Näide nr 7:
Kas kaks pöördarvu võib olla samaaegselt segatud arv?

Vaatame näidet. Võtame segamurru \(1\frac(1)(2)\, leiame selle pöördmurru, selleks teisendame selle valeks murruks \(1\frac(1)(2) = \frac(3 )(2) \) . Selle pöördmurd on võrdne \(\frac(2)(3)\) . Murd \(\frac(2)(3)\) on õige murd. Vastus: Kahte vastastikku pöördvõrdelist murdu ei saa korraga segada.

Kesk- ja KeskkoolÕpilased õppisid teemat “Murrud”. See mõiste on aga palju laiem kui õppeprotsessis ette antud. Tänapäeval kohtab murru mõistet üsna sageli ja mitte igaüks ei saa arvutada ühtegi avaldist, näiteks murdude korrutamist.

Mis on murdosa?

Ajalooliselt tekkisid murdarvud vajadusest mõõta. Nagu praktika näitab, on sageli näiteid segmendi pikkuse ja ristkülikukujulise ristküliku mahu määramise kohta.

Esialgu tutvustatakse õpilastele aktsia mõistet. Näiteks kui jagate arbuusi 8 osaks, saab iga inimene kaheksandiku arbuusist. Seda ühte kaheksast osa nimetatakse aktsiaks.

Osa, mis on võrdne ½ mis tahes väärtusest, nimetatakse pooleks; ⅓ - kolmas; ¼ - veerand. Kirjeid kujul 5/8, 4/5, 2/4 nimetatakse tavalisteks murrudeks. Harilik murd jaguneb lugejaks ja nimetajaks. Nende vahel on fraktsiooniriba või fraktsiooniriba. Murdjoont saab tõmmata kas horisontaalse või kaldus joonena. Sel juhul tähistab see jagamismärki.

Nimetaja tähistab, kui mitmeks võrdseks osaks suurus või objekt on jagatud; ja lugeja näitab, kui palju identseid aktsiaid võetakse. Lugeja kirjutatakse murrurea kohale, nimetaja selle alla.

Kõige mugavam on näidata tavalisi murde koordinaatkiirel. Kui üks segment on jagatud 4 võrdseks osaks, iga osa tähistatakse ladina tähega, võib tulemus olla suurepärane visuaalne abivahend. Seega näitab punkt A osa, mis on võrdne 1/4 kogu ühikulõigust, ja punkt B tähistab 2/8 antud segmendist.

Murdude tüübid

Murrud võivad olla tavalised, kümnendarvud ja segaarvud. Lisaks saab murde jagada õigeteks ja ebaõigeteks. See klassifikatsioon sobib rohkem tavaliste fraktsioonide jaoks.

Õige murd on arv, mille lugeja on nimetajast väiksem. Seega on vale murd arv, mille lugeja on nimetajast suurem. Teist tüüpi kirjutatakse tavaliselt seganumbrina. See avaldis koosneb täisarvust ja murdosast. Näiteks 1½. 1 - terve osa, ½ - murdosa. Kui teil on aga vaja avaldisega mõningaid manipulatsioone teha (murdude jagamine või korrutamine, nende vähendamine või teisendamine), teisendatakse segaarv valeks murdarvuks.

Õige murdosa on alati väiksem kui üks ja vale on alati suurem kui 1 või sellega võrdne.

Selle avaldise puhul peame silmas kirjet, milles on esindatud suvaline arv, mille murdosa avaldise nimetajat saab väljendada mitme nulliga ühega. Kui murdosa on õige, siis on terve osa kümnendmärk on võrdne nulliga.

Kümnendmurru kirjutamiseks tuleb esmalt kirjutada terve osa, eraldada see komaga murdosast ja seejärel kirjutada murdosa avaldis. Tuleb meeles pidada, et pärast koma peab lugejas olema sama arv digitaalseid märke kui nimetajas on nullid.

Näide. Väljendage murdarvu 7 21 / 1000 kümnendsüsteemis.

Algoritm valemurru teisendamiseks segaarvuks ja vastupidi

Ülesande vastuses vale murdu kirjutamine on vale, seetõttu tuleb see teisendada segaarvuks:

• jagage lugeja olemasoleva nimetajaga;
• V konkreetne näide mittetäielik jagatis - tervik;
• ja jääk on murdosa lugeja, kusjuures nimetaja jääb muutumatuks.

Näide. Teisenda vale murd segaarvuks: 47/5.

Lahendus. 47: 5. Osajagatis on 9, jääk = 2. Niisiis, 47 / 5 = 9 2 / 5.

Mõnikord peate segaarvu esitama valemurruna. Seejärel peate kasutama järgmist algoritmi:

• täisarvuline osa korrutatakse murdosa avaldise nimetajaga;
• saadud korrutis lisatakse lugejasse;
• tulemus kirjutatakse lugejasse, nimetaja jääb muutumatuks.

Näide. Esitage arv segakujul vale murdena: 9 8/10.

Lahendus. 9 x 10 + 8 = 90 + 8 = 98 on lugeja.

Vastus: 98 / 10.

Murdude korrutamine

Tavamurdudega saab sooritada erinevaid algebralisi tehteid. Kahe arvu korrutamiseks peate korrutama lugeja lugejaga ja nimetaja nimetajaga. Pealegi ei erine erinevate nimetajatega murdude korrutamine korrutisest murdarvud samade nimetajatega.

See juhtub, et pärast tulemuse leidmist peate murdosa vähendama. Saadud avaldist tuleb nii palju kui võimalik lihtsustada. Muidugi ei saa väita, et valemurd vastuses on viga, kuid seda on ka raske õigeks vastuseks nimetada.

Näide. Leidke kahe hariliku murru korrutis: ½ ja 20/18.

Nagu näitest näha, saadakse pärast korrutise leidmist taandatav murdosa. Nii lugeja kui ka nimetaja jagatakse sel juhul 4-ga ja tulemuseks on vastus 5/9.

Kümnendmurdude korrutamine

Kümnendmurdude korrutis on oma põhimõttelt üsna erinev tavamurdude korrutisest. Niisiis, murdude korrutamine on järgmine:

• kaks kümnendmurdu tuleb kirjutada üksteise alla nii, et kõige parempoolsemad numbrid oleksid üksteise all;
• peate korrutama kirjutatud arvud, hoolimata komadest, st naturaalarvudena;
• loe igas numbris koma järel olevate numbrite arv;
• pärast korrutamist saadud tulemuses peate lugema paremalt nii palju digitaalseid sümboleid, mis sisalduvad mõlema teguri summas pärast koma, ja panema eraldusmärgi;
• kui tootes on vähem numbreid, siis tuleb nende ette kirjutada nii palju nulle, et see arv katta, panna koma ja lisada kogu nulliga võrdne osa.

Näide. Arvutage kahe kümnendmurru korrutis: 2,25 ja 3,6.

Lahendus.

Segamurdude korrutamine

Kahe segamurru korrutise arvutamiseks peate kasutama murdude korrutamise reeglit:

• teisendada segaarvud valedeks murdudeks;
• leida lugejate korrutis;
• leida nimetajate korrutis;
• kirjutage tulemus üles;
• lihtsustage väljendit nii palju kui võimalik.

Näide. Leidke 4½ ja 6 2/5 korrutis.

Arvu korrutamine murdosaga (murrud arvuga)

Lisaks kahe murru ja segaarvu korrutise leidmisele on ülesandeid, kus tuleb korrutada murdosaga.

Niisiis, toote leidmiseks kümnend ja naturaalarvu, vajate:

• kirjuta arv murdosa alla nii, et kõige parempoolsemad numbrid oleksid üksteise kohal;
• leia toode vaatamata komale;
• saadud tulemuses eraldage täisarvuline osa murdosast komaga, lugedes paremalt poolt numbrite arvu, mis asuvad murdosas pärast koma.

Hariliku murru korrutamiseks arvuga tuleb leida lugeja ja naturaalteguri korrutis. Kui vastus annab murdosa, mida saab vähendada, tuleks see teisendada.

Näide. Arvutage 5/8 ja 12 korrutis.

Lahendus. 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

Vastus: 7 1 / 2.

Nagu eelmisest näitest näha, oli vaja saadud tulemust vähendada ja vale murdosa teisendada segaarvuks.

Murdude korrutamine puudutab ka segakujulise arvu ja naturaalteguri korrutise leidmist. Nende kahe arvu korrutamiseks peaksite korrutama kogu segateguri osa arvuga, korrutama lugeja sama väärtusega ja jätma nimetaja muutmata. Vajadusel peate saadud tulemust nii palju kui võimalik lihtsustama.

Näide. Leidke 9 5/6 ja 9 korrutis.

Lahendus. 9 5/6 x 9 = 9 x 9 + (5 x 9) / 6 = 81 + 45/6 = 81 + 7 3/6 = 88 1/2.

Vastus: 88 1 / 2.

korrutamine teguritega 10, 100, 1000 või 0,1; 0,01; 0,001

Järgmine reegel tuleneb eelmisest lõigust. Kümnendmurru korrutamiseks arvuga 10, 100, 1000, 10 000 jne tuleb koma nihutada paremale nii mitme numbri võrra, kui ühe järel on teguris nulle.

Näide 1. Leidke 0,065 ja 1000 korrutis.

Lahendus. 0,065 x 1000 = 0065 = 65.

Vastus: 65.

Näide 2. Leidke 3,9 ja 1000 korrutis.

Lahendus. 3,9 x 1000 = 3900 x 1000 = 3900.

Vastus: 3900.

Kui teil on vaja korrutada naturaalarv ja 0,1; 0,01; 0,001; 0,0001 jne, peaksite tulemuseks olevas korrutis koma vasakule nihutama nii palju tähemärke, kui palju on nulli enne ühte. Vajadusel kirjutatakse naturaalarvu ette piisav arv nulle.

Näide 1. Leidke 56 ja 0,01 korrutis.

Lahendus. 56 x 0,01 = 0056 = 0,56.

Vastus: 0,56.

Näide 2. Leidke 4 ja 0,001 korrutis.

Lahendus. 4 x 0,001 = 0004 = 0,004.

Vastus: 0,004.

Seega ei tohiks erinevate murdude korrutise leidmine raskusi tekitada, välja arvatud ehk tulemuse arvutamine; sel juhul ei saa te lihtsalt ilma kalkulaatorita hakkama.

Teine tehe, mida saab teha tavaliste murdudega, on korrutamine. Püüame selgitada selle põhireegleid ülesannete lahendamisel, näidata, kuidas harilik murd korrutatakse naturaalarvuga ja kuidas õigesti korrutada kolm harilikku murru või rohkem.

Esmalt paneme kirja põhireegli:

Definitsioon 1

Kui korrutame ühe hariliku murru, siis on saadud murru lugeja võrdne algsete murdude lugejate korrutisega ja nimetaja on võrdne nende nimetajate korrutisega. Sõnasõnalises vormis saab seda kahe murdosa a / b ja c / d korral väljendada kujul a b · c d = a · c b · d.

Vaatame näidet selle reegli õige rakendamise kohta. Oletame, et meil on ruut, mille külg on võrdne ühe arvühikuga. Siis on joonise pindala 1 ruut. üksus. Kui jagame ruudu võrdseteks ristkülikuteks, mille küljed on võrdsed 1 4 ja 1 8 arvühikuga, saame, et see koosneb nüüd 32 ristkülikust (sest 8 4 = 32). Sellest lähtuvalt on igaühe pindala võrdne 1 32-ga kogu joonise pindalast, s.o. 132 ruutmeetrit ühikut.

Meil on varjutatud fragment, mille küljed on võrdsed 5 8 arvühikuga ja 3 4 numbriühikuga. Sellest lähtuvalt peate selle pindala arvutamiseks korrutama esimese murdosa teisega. See võrdub 5 8 · 3 4 ruutmeetriga. ühikut. Kuid võime lihtsalt kokku lugeda, mitu ristkülikut fragmendis on: neid on 15, mis tähendab kogupindala on 15 32 ruutühikut.

Kuna 5 3 = 15 ja 8 4 = 32, saame kirjutada järgmise võrdsuse:

5 8 3 4 = 5 3 8 4 = 15 32

See kinnitab reeglit, mille me sõnastasime harilike murdude korrutamiseks, mis on väljendatud kujul a b · c d = a · c b · d. See töötab sama nii õige kui ka jaoks ebaõiged murded; Seda saab kasutada nii erinevate kui ka identsete nimetajatega murdude korrutamiseks.

Vaatame lahendusi mitmele probleemile, mis on seotud harilike murdude korrutamisega.

Näide 1

Korrutage 7 11 9 8-ga.

Lahendus

Esiteks arvutame näidatud murdude lugejate korrutise, korrutades 7 9-ga. Meil on 63. Seejärel arvutame nimetajate korrutise ja saame: 11 · 8 = 88. Koostame kaks arvu ja vastus on: 63 88.

Kogu lahenduse saab kirjutada järgmiselt:

7 11 9 8 = 7 9 11 8 = 63 88

Vastus: 7 11 · 9 8 = 63 88.

Kui saame oma vastuses taandatava murdosa, peame arvutuse lõpule viima ja selle redutseerima. Kui saame vale murdu, peame kogu osa sellest eraldama.

Näide 2

Arvutage murdarvude korrutis 4 15 ja 55 6 .

Lahendus

Eespool uuritud reegli kohaselt peame korrutama lugeja lugejaga ja nimetaja nimetajaga. Lahenduse kirje näeb välja selline:

4 15 55 6 = 4 55 15 6 = 220 90

Saime taandatava murdosa, st. üks, mis jagub 10-ga.

Vähendame murdosa: 220 90 gcd (220, 90) = 10, 220 90 = 220: 10 90: 10 = 22 9. Selle tulemusena saime vale murru, millest valime kogu osa ja saame segaarvu: 22 9 = 2 4 9.

Vastus: 4 15 55 6 = 2 4 9.

Arvutamise hõlbustamiseks saame enne korrutustehte sooritamist ka algseid murde vähendada, selleks peame murde taandada kujule a · c b · d. Jagame muutujate väärtused lihtsateks teguriteks ja vähendame samu.

Selgitame, kuidas see konkreetse ülesande andmeid kasutades välja näeb.

Näide 3

Arvutage korrutis 4 15 55 6.

Lahendus

Kirjutame üles arvutused korrutusreegli alusel. Me saame:

4 15 55 6 = 4 55 15 6

Kuna 4 = 2 2, 55 = 5 11, 15 = 3 5 ja 6 = 2 3, siis 4 55 15 6 = 2 2 5 11 3 5 2 3.

2 11 3 3 = 22 9 = 2 4 9

Vastus: 4 15 · 55 6 = 2 4 9 .

Arvulisel avaldisel, milles harilikud murded korrutatakse, on kommutatiivne omadus, see tähendab, et vajadusel saame tegurite järjekorda muuta:

a b · c d = c d · a b = a · c b · d

Kuidas korrutada murdosa naturaalarvuga

Paneme põhireegli kohe kirja ja proovime siis seda praktikas selgitada.

2. definitsioon

Hariliku murru korrutamiseks naturaalarvuga peate korrutama selle murru lugeja selle arvuga. Sel juhul on lõpliku murdosa nimetaja võrdne originaali nimetajaga harilik murd. Teatud murdosa a b korrutamise naturaalarvuga n saab kirjutada valemiga a b · n = a · n b.

Seda valemit on lihtne mõista, kui mäletate, et mis tahes naturaalarvu saab esitada tavalise murdena, mille nimetaja on võrdne ühega, see tähendab:

a b · n = a b · n 1 = a · n b · 1 = a · n b

Selgitagem oma ideed konkreetsete näidetega.

Näide 4

Arvutage korrutis 2 27 korda 5.

Lahendus

Kui korrutada algmurru lugeja teise teguriga, saame 10. Ülalkirjeldatud reegli kohaselt saame tulemuseks 10 27. Kogu lahendus on toodud selles postituses:

2 27 5 = 2 5 27 = 10 27

Vastus: 2 27 5 = 10 27

Kui korrutame naturaalarvu murdosaga, peame sageli tulemust lühendama või esitama segaarvuna.

Näide 5

Tingimus: arvutage korrutis 8 korda 5 12.

Lahendus

Vastavalt ülaltoodud reeglile korrutame naturaalarvu lugejaga. Selle tulemusena saame, et 5 12 8 = 5 8 12 = 40 12. Lõplikul murdosal on 2-ga jaguvuse märgid, seega peame seda vähendama:

LCM (40, 12) = 4, seega 40 12 = 40: 4 12: 4 = 10 3

Nüüd jääb meil vaid kogu osa välja valida ja valmis vastus kirja panna: 10 3 = 3 1 3.

Selles kirjes näete kogu lahendust: 5 12 8 = 5 8 12 = 40 12 = 10 3 = 3 1 3.

Samuti saaksime murdosa vähendada, arvutades lugeja ja nimetaja algteguriteks ja tulemus oleks täpselt sama.

Vastus: 5 12 8 = 3 1 3.

Arvulisel avaldisel, milles naturaalarv korrutatakse murdosaga, on samuti nihke omadus, see tähendab, et tegurite järjekord ei mõjuta tulemust:

a b · n = n · a b = a · n b

Kuidas korrutada kolm või enam harilikku murru

Harilike murdude korrutamise tegevusele saame laiendada samu omadusi, mis on iseloomulikud naturaalarvude korrutamisele. See tuleneb nende mõistete definitsioonist.

Tänu kombineerimis- ja kommutatiivsete omaduste tundmisele saate korrutada kolme või enama hariliku murru. Suurema mugavuse huvides on vastuvõetav tegurite ümberpaigutamine või sulgude paigutamine viisil, mis hõlbustab loendamist.

Näitame näitega, kuidas seda tehakse.

Näide 6

Korrutage neli tavalist murdu 1 20, 12 5, 3 7 ja 5 8.

Lahendus: Esmalt salvestame töö. Saame 1 20 · 12 5 · 3 7 · 5 8 . Peame kõik lugejad ja nimetajad kokku korrutama: 1 20 · 12 5 · 3 7 · 5 8 = 1 · 12 · 3 · 5 20 · 5 · 7 · 8 .

Enne kui hakkame korrutama, saame asju enda jaoks veidi lihtsamaks teha ja lisada mõned arvud edasise vähendamise algteguriteks. See on lihtsam kui juba ettevalmistatud fraktsiooni vähendamine.

1 12 3 5 20 5 7 8 = 1 (2 2 3) 3 5 2 2 5 5 7 (2 2 2) = 3 3 5 7 2 2 2 = 9 280

Vastus: 1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 9280.

Näide 7

Korrutage 5 arvu 7 8 · 12 · 8 · 5 36 · 10 .

Lahendus

Mugavuse huvides saame rühmitada murdarvu 7 8 numbriga 8 ja arvu 12 murdarvuga 5 36, kuna tulevased lühendid on meile ilmsed. Selle tulemusena saame:
7 8 12 8 5 36 10 = 7 8 8 12 5 36 10 = 7 8 8 12 5 36 10 = 7 1 2 2 3 5 2 2 3 3 10 = 7 5 3 10 = 7 = 5 31 6 3 2 3

Vastus: 7 8 12 8 5 36 10 = 116 2 3.

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

Oletame, et Achilleus jookseb kümme korda kiiremini kui kilpkonn ja on sellest tuhat sammu maas. Aja jooksul, mis kulub Achilleuse läbimiseks, roomab kilpkonn sada sammu samas suunas. Kui Achilleus jookseb sada sammu, roomab kilpkonn veel kümme sammu jne. Protsess jätkub lõpmatuseni, Achilleus ei jõua kilpkonnale kunagi järele.

See arutluskäik sai loogiliseks šokiks kõigile järgnevatele põlvkondadele. Aristoteles, Diogenes, Kant, Hegel, Hilbert... Nad kõik pidasid ühel või teisel viisil Zenoni apooriat. Šokk oli nii tugev, et " ...arutelud jätkuvad tänaseni, et jõuda ühisele arvamusele paradokside olemuse üle teadusringkond siiani pole see võimalik olnud... olime kaasatud teema uurimisse matemaatiline analüüs, hulgateooria, uued füüsikalised ja filosoofilised lähenemised; ükski neist ei saanud probleemi üldtunnustatud lahenduseks..."[Wikipedia, "Zeno's Aporia". Kõik saavad aru, et neid lollitatakse, aga keegi ei saa aru, milles pettus seisneb.

Matemaatilisest vaatenurgast näitas Zenon oma apooriates selgelt üleminekut kvantiteedilt . See üleminek eeldab rakendust püsivate asemel. Minu arusaamist mööda pole muutuvate mõõtühikute kasutamise matemaatilist aparaati kas veel välja töötatud või pole seda Zenoni apooria puhul rakendatud. Meie tavapärase loogika rakendamine viib meid lõksu. Me rakendame mõtlemise inertsi tõttu vastastikusele väärtusele konstantseid ajaühikuid. Füüsilisest vaatenurgast näeb see välja nagu aeg aeglustub, kuni see täielikult peatub hetkel, mil Achilleus kilpkonnale järele jõuab. Kui aeg peatub, ei suuda Achilleus enam kilpkonnast üle joosta.

Kui pöörame oma tavapärase loogika ümber, loksub kõik paika. Achilleus jookseb ühtlase kiirusega. Tema tee iga järgmine lõik on kümme korda lühem kui eelmine. Sellest tulenevalt on selle ületamiseks kulunud aeg kümme korda väiksem kui eelmisel. Kui rakendame selles olukorras "lõpmatuse" mõistet, siis oleks õige öelda: "Achilleus jõuab kilpkonnale lõpmatult kiiresti järele."

Kuidas seda loogilist lõksu vältida? Jääge konstantsetesse ajaühikutesse ja ärge lülituge vastastikustele ühikutele. Zenoni keeles näeb see välja järgmine:

Aja jooksul, mis kulub Achilleuse tuhande sammu jooksmiseks, roomab kilpkonn sada sammu samas suunas. Järgmise esimesega võrdse ajaintervalli jooksul jookseb Achilleus veel tuhat sammu ja kilpkonn roomab sada sammu. Nüüd on Achilleus kilpkonnast kaheksasada sammu ees.

See lähenemine kirjeldab adekvaatselt tegelikkust ilma loogiliste paradoksideta. Kuid see pole probleemi täielik lahendus. Einsteini väide valguse kiiruse vastupandamatusest on väga sarnane Zenoni apooriaga "Achilleus ja kilpkonn". Seda probleemi tuleb veel uurida, ümber mõelda ja lahendada. Ja lahendust tuleb otsida mitte lõpmata suurtes arvudes, vaid mõõtühikutes.

Veel üks Zenoni huvitav apooria räägib lendavast noolest:

Lendav nool on liikumatu, kuna ta on igal ajahetkel puhkeolekus ja kuna ta on igal ajahetkel puhkab, siis on ta alati puhkeolekus.

Selles apoorias ületatakse loogiline paradoks väga lihtsalt - piisab, kui selgitada, et igal ajahetkel on lendav nool paigal erinevates ruumipunktides, mis tegelikult on liikumine. Siin tuleb märkida veel üks punkt. Ühe maanteel oleva auto foto järgi on võimatu kindlaks teha ei selle liikumise fakti ega kaugust selleni. Et teha kindlaks, kas auto liigub, vajate kahte fotot, mis on tehtud ühest ja samast punktist erinevatel ajahetkedel, kuid te ei saa määrata nende kaugust. Auto kauguse määramiseks on vaja kahte pilti, mis on tehtud ühel ajahetkel erinevatest ruumipunktidest, kuid nende järgi ei saa liikumise fakti kindlaks teha (loomulikult vajate arvutusteks siiski lisaandmeid, trigonomeetria aitab teid ). Erilist tähelepanu tahan juhtida asjaolule, et kaks ajapunkti ja kaks punkti ruumis on erinevad asjad, mida ei tohiks segi ajada, sest need annavad erinevaid võimalusi uurimistöö jaoks.

Kolmapäeval, 4. juulil 2018

Vikipeedias on väga hästi kirjeldatud komplekti ja multikomplekti erinevusi. Vaatame.

Nagu näete, "komplektis ei saa olla kahte identset elementi", kuid kui komplektis on identsed elemendid, nimetatakse sellist komplekti "multiseks". Selline absurdne loogika tundlikud olendid ei saa kunagi aru. See on tase rääkivad papagoid ja treenitud ahvid, kellel puudub mõistus sõnast "täiesti". Matemaatikud tegutsevad tavaliste koolitajatena, kuulutades meile oma absurdseid ideid.

Kunagi olid silla ehitanud insenerid silda katsetades silla all paadis. Kui sild kokku kukkus, suri keskpärane insener oma loomingu rusude all. Kui sild koormusele vastu pidas, ehitas andekas insener teisi sildu.

Pole tähtis, kuidas matemaatikud peituvad fraasi "mind me, I'm in the house" taha või õigemini: "matemaatika uurib abstraktseid mõisteid", on üks nabanöör, mis seob neid lahutamatult reaalsusega. See nabanöör on raha. Kohaldatav matemaatiline teooria seab matemaatikutele endile.

Õppisime väga hästi matemaatikat ja nüüd istume kassa taga ja anname palka välja. Nii et matemaatik tuleb meie juurde oma raha pärast. Loeme talle kogu summa välja ja laotame oma lauale erinevatesse hunnikutesse, millesse paneme sama nimiväärtusega arveid. Seejärel võtame igast virnast ühe arve ja anname selle matemaatikule." matemaatiline komplekt palgad." Selgitame matemaatikule, et allesjäänud arved saab ta kätte alles siis, kui ta tõestab, et ilma identsete elementideta hulk ei võrdu identsete elementidega hulgaga. Siit algab lõbus.

Esiteks hakkab tööle saadikute loogika: "Seda võib teistele rakendada, aga mulle mitte!" Siis hakkavad nad meile kinnitama, et sama nimiväärtusega vekslitel on erinevad arvenumbrid, mis tähendab, et neid ei saa pidada samadeks elementideks. Olgu, loeme palgad müntidesse – müntidel pole numbreid. Siin hakkab matemaatik paaniliselt meenutama füüsikat: erinevatel müntidel on erinev kogus mustust, kristallstruktuur ja aatomite paigutus on igal mündil unikaalne...

Ja nüüd on mul kõige huvitavam küsimus: kus on piir, millest kaugemale muutuvad multikomplekti elemendid hulga elementideks ja vastupidi? Sellist joont pole olemas – kõike otsustavad šamaanid, teadus ei ole siin lähedalgi valetamisele.

Vaata siia. Valime jalgpallistaadionid sama põllupinnaga. Väljade pindalad on samad – see tähendab, et meil on multikomplekt. Aga kui vaadata nende samade staadioninimesid, siis saame neid palju, sest nimed on erinevad. Nagu näete, on sama elementide komplekt nii hulk kui ka multikomplekt. Kumb on õige? Ja siin tõmbab matemaatik-šamaan-teramees varrukast trumpide ässa ja hakkab meile rääkima kas komplektist või multikomplektist. Igal juhul veenab ta meid, et tal on õigus.

Et mõista, kuidas tänapäeva šamaanid hulgateooriaga opereerivad, sidudes selle reaalsusega, piisab, kui vastata ühele küsimusele: mille poolest erinevad ühe hulga elemendid teise hulga elementidest? Ma näitan teile, ilma igasuguse "mõeldava mitte ühe tervikuna" või "ei ole mõeldav ühtse tervikuna".

Pühapäev, 18. märts 2018

Arvu numbrite summa on šamaanide tants tamburiiniga, millel pole matemaatikaga mingit pistmist. Jah, matemaatikatundides õpetatakse meid leidma arvu numbrite summat ja seda kasutama, aga seepärast ongi nad šamaanid, et õpetada järeltulijatele nende oskusi ja tarkust, muidu surevad šamaanid lihtsalt välja.

Kas vajate tõestust? Avage Wikipedia ja proovige leida leht "Arvu numbrite summa". Teda pole olemas. Matemaatikas pole valemit, mille abil saaks leida mis tahes arvu numbrite summa. Lõppude lõpuks on numbrid graafilised sümbolid, mille abil kirjutame numbreid ja matemaatika keeles kõlab ülesanne nii: "Leia suvalist arvu esindavate graafiliste sümbolite summa." Matemaatikud ei suuda seda ülesannet lahendada, kuid šamaanid saavad sellega hõlpsasti hakkama.

Mõelgem välja, mida ja kuidas teeme, et leida antud arvu numbrite summa. Ja nii, olgu meil number 12345. Mida tuleb teha, et leida selle arvu numbrite summa? Vaatleme kõiki samme järjekorras.

1. Kirjutage number paberile. Mida me oleme teinud? Oleme teisendanud numbri graafiliseks numbrisümboliks. See ei ole matemaatiline tehe.

2. Lõikasime ühe saadud pildi mitmeks üksikuid numbreid sisaldavaks pildiks. Pildi lõikamine ei ole matemaatiline tehe.

3. Teisendage üksikud graafilised sümbolid numbriteks. See ei ole matemaatiline tehe.

4. Lisage saadud numbrid. Nüüd on see matemaatika.

Arvu 12345 numbrite summa on 15. Need on šamaanide õpetatavad “lõikamis- ja õmbluskursused”, mida matemaatikud kasutavad. Kuid see pole veel kõik.

Matemaatilisest seisukohast pole vahet, millisesse arvusüsteemi me arvu kirjutame. Niisiis, sisse erinevad süsteemid Arvutuses on sama arvu numbrite summa erinev. Matemaatikas märgitakse numbrisüsteem numbrist paremal oleva alaindeksina. KOOS suur hulk 12345 Ma ei taha oma pead petta, vaatame numbrit 26 artiklist . Kirjutame selle arvu kahend-, kaheksand-, kümnend- ja kuueteistkümnendsüsteemis. Me ei vaata iga sammu mikroskoobi all, me oleme seda juba teinud. Vaatame tulemust.

Nagu näete, on erinevates numbrisüsteemides sama numbri numbrite summa erinev. Sellel tulemusel pole matemaatikaga mingit pistmist. See on sama, kui määraksite ristküliku pindala meetrites ja sentimeetrites, saaksite täiesti erinevad tulemused.

Null näeb kõigis numbrisüsteemides välja ühesugune ja sellel pole numbrite summat. See on veel üks argument selle kasuks, et. Küsimus matemaatikutele: kuidas on matemaatikas määratud midagi, mis ei ole arv? Mis, matemaatikute jaoks ei eksisteeri midagi peale numbrite? Ma võin seda lubada šamaanidele, kuid mitte teadlastele. Tegelikkus ei seisne ainult numbrites.

Saadud tulemust tuleks pidada tõestuseks, et arvusüsteemid on arvude mõõtühikud. Me ei saa ju võrrelda numbreid erinevate mõõtühikutega. Kui samad toimingud sama suuruse erinevate mõõtühikutega annavad pärast nende võrdlemist erinevaid tulemusi, siis pole sellel matemaatikaga mingit pistmist.

Mis on tõeline matemaatika? See on siis, kui matemaatilise tehte tulemus ei sõltu arvu suurusest, kasutatavast mõõtühikust ja sellest, kes selle toimingu sooritab.

Oh! Kas see pole mitte naiste tualett?
- Noor naine! See on laboratoorium hingede indefiilse pühaduse uurimiseks nende taevasse tõusmise ajal! Halo peal ja nool üles. Mis tualett veel?

Naine... Halo peal ja nool alla on isased.

Kui selline disainikunstiteos vilksatab teie silme ees mitu korda päevas,

Siis pole üllatav, et äkki leiate oma autost kummalise ikooni:

Mina isiklikult pingutan selle nimel, et kakaval inimesel oleks näha miinus nelja kraadi (üks pilt) (mitmest pildist koosnev kompositsioon: miinusmärk, number neli, kraadide tähistus). Ja ma ei arva, et see tüdruk on loll, kes füüsikat ei tunne. Tal on lihtsalt taju stereotüüp graafilised pildid. Ja matemaatikud õpetavad seda meile kogu aeg. Siin on näide.

1A ei ole "miinus neli kraadi" ega "üks a". See on "kakav mees" või number "kakskümmend kuus" kuueteistkümnendsüsteemis. Need inimesed, kes pidevalt selles numbrisüsteemis töötavad, tajuvad numbrit ja tähte automaatselt ühe graafilise sümbolina.

SAAGE JUBA NEIST REHAIDEST ÜLE! 🙂

Murdude korrutamine ja jagamine.

Tähelepanu!
On täiendavaid
materjalid erijaos 555.
Neile, kes on väga “mitte väga. »
Ja neile, kes “väga. ")

See toiming on palju meeldivam kui liitmine ja lahutamine! Sest see on lihtsam. Tuletame meelde, et murdosa korrutamiseks murdosaga peate korrutama lugejad (see on tulemuse lugeja) ja nimetajad (see on nimetaja). See on:

Kõik on äärmiselt lihtne. Ja palun ärge otsige ühist nimetajat! Siin pole teda vaja...

Murru jagamiseks murdosaga peate tagurdama teiseks(see on oluline!) murdosa ja korrutage need, st:

Kui puutute kokku täisarvude ja murdudega korrutamise või jagamisega, on kõik korras. Nagu liitmisegi puhul, teeme täisarvust murdosa, mille nimetaja on üks – ja jätka! Näiteks:

Keskkoolis tuleb sageli tegeleda kolmekorruseliste (või isegi neljakorruseliste!) murdudega. Näiteks:

Kuidas ma saan selle murdosa korralikuks muuta? Jah, väga lihtne! Kasutage kahepunktilist jaotust:

Kuid ärge unustage jagamise järjekorda! Erinevalt korrutamisest on see siin väga oluline! Muidugi ei aja me 4:2 ega 2:4 segi. Kuid kolmekorruselises murdosas on lihtne eksida. Pange tähele näiteks:

Esimesel juhul (avaldis vasakul):

Teises (avaldis paremal):

Kas tunnete erinevust? 4 ja 1/9!

Mis määrab jagamise järjekorra? Kas sulgudega või (nagu siin) horisontaalsete joonte pikkusega. Arendage oma silma. Ja kui sulgusid või sidekriipse pole, näiteks:

siis jaga ja korruta järjekorras, vasakult paremale!

Ja veel üks väga lihtne ja oluline tehnika. Kraadidega tegudes on see teile nii kasulik! Jagame ühe suvalise murdosaga, näiteks 13/15-ga:

Lask on ümber läinud! Ja seda juhtub alati. Jagades 1 suvalise murruga, on tulemuseks sama murd, ainult tagurpidi.

See on kõik murdarvudega tehte jaoks. Asi on üsna lihtne, kuid annab rohkem kui piisavalt vigu. Võtke arvesse praktilisi nõuandeid ja neid (vigu) jääb vähemaks!

1. Murdlausetega töötamisel on kõige olulisem täpsus ja tähelepanelikkus! Need ei ole üldised sõnad, mitte head soovid! See on hädasti vajalik! Tehke kõik ühtse riigieksami arvutused täisväärtusliku ülesandena, keskendunult ja selgelt. Parem on kirjutada mustandisse kaks lisarida, kui peast arvutades segadusse ajada.

2. Näidetes koos erinevad tüübid murrud – liikuge edasi tavaliste murdude juurde.

3. Vähendame kõiki murde, kuni need peatuvad.

4. Redendame mitmetasandilised murdavaldised tavalisteks, kasutades jagamist läbi kahe punkti (jälgime jagamise järjekorda!).

Siin on ülesanded, mida peate kindlasti täitma. Vastused antakse pärast kõiki ülesandeid. Kasutage selle teema materjale ja praktilisi näpunäiteid. Hinnake, kui palju näiteid suutsite õigesti lahendada. Esimene kord! Ilma kalkulaatorita! Ja tehke õiged järeldused.

Pea meeles – õige vastus on teisest (eriti kolmandast) korrast saadud ei lähe arvesse! Selline on karm elu.

Niisiis, lahendada eksamirežiimis ! See on muide juba ettevalmistus ühtseks riigieksamiks. Lahendame näite, kontrollime seda, lahendame järgmise. Otsustasime kõik – kontrollisime uuesti esimesest viimaseni. Aga ainult Siis vaata vastuseid.

Otsime vastuseid, mis vastavad teie omadele. Kirjutasin need meelega segamini, eemale nii-öelda kiusatusest. Siin need on, semikooloniga eraldatud vastused.

0; 17/22; 3/4; 2/5; 1; 25.

Nüüd teeme järeldused. Kui kõik õnnestus, olen teie üle õnnelik! Põhilised arvutused murdarvudega pole teie probleem! Saate teha tõsisemaid asju. Kui ei.

Nii et teil on üks kahest probleemist. Või mõlemad korraga.) Teadmiste puudumine ja (või) tähelepanematus. Aga. See lahendatav Probleemid.

Kõiki neid (ja rohkemgi!) näiteid käsitletakse erijaotises 555 “Murrud”. Üksikasjalike selgitustega, mida, miks ja kuidas. See analüüs aitab palju teadmiste ja oskuste puudumise korral!

Jah, ja teises probleemis on seal midagi.) Päris praktilisi nõuandeid, kuidas saada tähelepanelikumaks. Jah Jah! Nõuanded, mida saab rakendada iga.

Edu eeldab lisaks teadmistele ja tähelepanelikkusele teatud automaatsust. Kust seda saada? Kuulen rasket ohkamist... Jah, ainult praktikas, mitte kusagil mujal.

Treenimiseks võite minna veebisaidile 321start.ru. Valikus „Proovi” on igaühe jaoks 10 näidet. Kiire kinnitusega. Registreeritud kasutajatele - 34 näidet lihtsast raskeni. See on ainult murdosades.

Kui teile meeldib see sait.

Muide, mul on teie jaoks veel paar huvitavat saiti.)

Siin saad harjutada näidete lahendamist ja teada saada oma taset. Testimine kiirkinnitusega. Õpime - huviga!)

Ja siin saate tutvuda funktsioonide ja tuletistega.

1. reegel.

Murru korrutamiseks naturaalarvuga peate korrutama selle lugeja selle arvuga ja jätma nimetaja muutmata.

2. reegel.

Murru korrutamiseks murdosaga:

1. leidke nende murdude lugejate ja nimetajate korrutis

2. Kirjutage esimene korrutis lugejaks ja teine ​​nimetajaks.

3. reegel.

Segaarvude korrutamiseks peate need kirjutama valede murdudena ja seejärel kasutama murdude korrutamise reeglit.

4. reegel.

Ühe murdosa teisega jagamiseks peate dividendi korrutama jagaja pöördarvuga.

Näide 1.

Arvutama

Näide 2.

Arvutama

Näide 3.

Arvutama

Näide 4.

Arvutama

Matemaatika. Muud materjalid

Arvu tõstmine ratsionaalse astmeni. (

Arvu tõstmine loomuliku astmeni. (

Üldistatud intervallmeetod algebraliste võrratuste lahendamiseks (Autor A.V. Kolchanov)

Meetod tegurite asendamiseks algebralise ebavõrdsuse lahendamisel (Autor Kolchanov A.V.)

Jaguvuse märgid (Lungu Alena)

Pane end proovile teemal "Tavamurdude korrutamine ja jagamine"

Murdude korrutamine

Vaatleme tavaliste murdude korrutamist mitmes võimalikus variandis.

Hariliku murru korrutamine murdosaga

See on kõige lihtsam juhtum, mille puhul peate kasutama järgmist murdude korrutamise reeglid.

To korrutada murdosa murdosaga, vajalik:

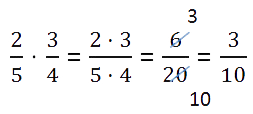
Enne lugejate ja nimetajate korrutamist kontrollige, kas murde saab vähendada. Murdude vähendamine arvutustes muudab teie arvutused palju lihtsamaks.

Murru korrutamine naturaalarvuga

Et teha murdosa korrutada naturaalarvuga Peate korrutama murdosa lugeja selle arvuga ja jätma murdosa nimetaja muutmata.

Kui korrutamise tulemus on vale murd, ärge unustage muuta seda segaarvuks, st tõstke esile kogu osa.

Segaarvude korrutamine

Segaarvude korrutamiseks peate need esmalt muutma valedeks murdudeks ja seejärel korrutama vastavalt tavaliste murdude korrutamise reeglile.

Teine võimalus murdosa korrutamiseks naturaalarvuga

Mõnikord on arvutuste tegemisel mugavam kasutada mõnda muud meetodit hariliku murru arvuga korrutamiseks.

Murru korrutamiseks naturaalarvuga peate jagama murdosa nimetaja selle arvuga ja jätma lugeja samaks.

Nagu näitest näha, on seda reegli versiooni mugavam kasutada, kui murdosa nimetaja jagub naturaalarvuga ilma jäägita.

Murru jagamine arvuga

Kuidas on kiireim viis murdosa arvuga jagada? Analüüsime teooriat, teeme järelduse ja kasutame näiteid, kuidas saab uue lühikese reegli abil murda arvuga jagada.

Tavaliselt järgib murdosa jagamine arvuga murdude jagamise reeglit. Korrutame esimese arvu (murru) teise pöördarvuga. Kuna teine ​​arv on täisarv, on selle pöördarvuks murd, mille lugeja on võrdne ühega ja nimetaja on võrdne antud arvuga. Skemaatiliselt näeb murdosa jagamine naturaalarvuga välja järgmine:

Sellest järeldame:

Murru jagamiseks arvuga peate korrutama nimetaja selle arvuga ja jätma lugeja samaks. Reegli võib sõnastada veelgi lühidalt:

Murru jagamisel arvuga läheb arv nimetajasse.

Jagage murdosa arvuga:

Murru jagamiseks arvuga kirjutame lugeja muutmata kujul ümber ja korrutame nimetaja selle arvuga. Vähendame 6 ja 3 3 võrra.

Murru jagamisel arvuga kirjutame lugeja ümber ja korrutame nimetaja selle arvuga. Vähendame 16 ja 24 8 võrra.

Murru jagamisel arvuga läheb arv nimetajasse, seega jätame lugeja samaks ja korrutame nimetaja jagajaga. Vähendame 21 ja 35 7 võrra.

Murdude korrutamine ja jagamine

Eelmisel korral õppisime murdude liitmist ja lahutamist (vt õppetükki “Murdude liitmine ja lahutamine”). Nende toimingute kõige keerulisem osa oli murdude ühise nimetajani viimine.

Nüüd on aeg tegeleda korrutamise ja jagamisega. Head uudised on see, et need toimingud on isegi lihtsamad kui liitmine ja lahutamine. Esmalt vaatleme lihtsaimat juhtumit, kui on kaks positiivset murdu ilma eraldatud täisarvuta.

Kahe murru korrutamiseks peate nende lugejad ja nimetajad eraldi korrutama. Esimene number on uue murru lugeja ja teine ​​on nimetaja.

Kahe murru jagamiseks peate korrutama esimese murdosa "ümberpööratud" teise murruga.

Definitsioonist järeldub, et murdude jagamine taandub korrutamiseks. Murru ümberpööramiseks vahetage lihtsalt lugeja ja nimetaja. Seetõttu käsitleme kogu õppetunni jooksul peamiselt korrutamist.

Korrutamise tulemusena võib tekkida (ja sageli tekib) taandatav murd – seda tuleb loomulikult vähendada. Kui pärast kõiki vähendamisi osutub murdosa valeks, tuleks kogu osa esile tõsta. Mida aga korrutamisega kindlasti ei juhtu, on taandamine ühisele nimetajale: ei mingeid ristimeetodeid, suurimaid tegureid ja väikseimaid ühiseid kordusi.

Ülesanne. Leidke väljendi tähendus:

Definitsiooni järgi on meil:

Murdude korrutamine täisosadega ja negatiivsete murdudega

Kui murrud sisaldavad täisarvu, tuleb need teisendada sobimatuteks osadeks ja alles seejärel korrutada vastavalt ülaltoodud skeemidele.

Kui murdosa lugejas, nimetajas või selle ees on miinus, saab selle korrutisest välja võtta või üldse eemaldada vastavalt järgmistele reeglitele:

1. Pluss miinusega annab miinuse;
2. Kaks negatiivset teevad jaatava.

Seni on neid reegleid kohanud vaid negatiivsete murdude liitmisel ja lahutamisel, kui oli vaja tervest osast lahti saada. Teose puhul saab neid üldistada, et "põletada" mitu puudust korraga:

3. Negatiivid kriipsutame paarikaupa maha, kuni need täielikult kaovad. Äärmuslikel juhtudel võib ellu jääda üks miinus - see, mille jaoks polnud kaaslast;
4. Kui miinuseid ei jää, on toiming lõpetatud - võite hakata korrutama. Kui viimast miinust ei kriipsutata maha, sest selle jaoks polnud paari, võtame selle korrutamise piiridest välja. Tulemuseks on negatiivne murd.

Teisendame kõik murrud valedeks ja seejärel võtame korrutamisest välja miinused. Korrutame järelejäänud tavapäraste reeglite järgi. Saame:

Tuletan teile veel kord meelde, et esiletõstetud täisosaga murru ette ilmuv miinus viitab konkreetselt kogu murrule, mitte ainult selle tervele osale (see kehtib kahe viimase näite kohta).

Pange tähele ka negatiivsed arvud: Korrutamisel on need sulgudes. Seda tehakse selleks, et eraldada miinused korrutusmärkidest ja muuta kogu tähistus täpsemaks.

Murdude vähendamine lennult

Korrutamine on väga töömahukas toiming. Siin olevad numbrid osutuvad üsna suurteks ja probleemi lihtsustamiseks võite proovida murdosa veelgi vähendada enne korrutamist. Tõepoolest, sisuliselt on murdude lugejad ja nimetajad tavalised tegurid ja seetõttu saab neid taandada, kasutades murdosa põhiomadust. Heitke pilk näidetele:

Kõikides näidetes on punasega märgitud numbrid, mida on vähendatud ja mis neist järele jääb.

Pange tähele: esimesel juhul vähendati kordajaid täielikult. Nende asemele jäävad üksused, mida üldiselt ei pea kirjutama. Teise näite puhul ei olnud võimalik saavutada täielikku vähendamist, kuid arvutuste kogusumma siiski vähenes.

Kuid ärge kunagi kasutage seda tehnikat murdude liitmisel ja lahutamisel! Jah, mõnikord on sarnaseid numbreid, mida soovite lihtsalt vähendada. Vaata siit:

Sa ei saa seda teha!

Viga tekib seetõttu, et liitmisel annab murdosa lugeja summa, mitte arvude korrutise. Järelikult on võimatu rakendada murru põhiomadust, kuna see omadus käsitleb konkreetselt arvude korrutamist.

Murdude vähendamiseks pole lihtsalt muid põhjuseid, seega näeb eelmise probleemi õige lahendus välja järgmine:

Nagu näha, osutus õige vastus mitte nii ilus. Üldiselt olge ettevaatlik.

Murrude jagamine.

Murru jagamine naturaalarvuga.

Näited murdosa jagamisest naturaalarvuga

Naturaalarvu jagamine murdosaga.

Näited naturaalarvu jagamisest murdosaga

Harilike murdude jagamine.

Näited harilike murdude jagamisest

Segaarvude jagamine.

Ühe segaarvu teisega jagamiseks peate:
• teisendada segafraktsioonid valedeks fraktsioonideks;
• korrutage esimene murd teise pöördarvuga;
• vähendada saadud fraktsiooni;
• Kui saate vale murdosa, teisendage vale murd segafraktsiooniks.

Segaarvude jagamise näited

1 1 2: 2 2 3 = 1 2 + 1 2: 2 3 + 2 3 = 3 2: 8 3 = 3 2 3 8 = 3 3 2 8 = 9 16

2 1 7: 3 5 = 2 7 + 1 7: 3 5 = 15 7: 3 5 = 15 7 5 3 = 15 5 7 3 = 5 5 7 = 25 7 = 7 3 + 4 7 = 3 4 7

Kõik ebasündsad kommentaarid kustutatakse ja nende autorid kantakse musta nimekirja!

Tere tulemast OnlineMSkooli.
Minu nimi on Dovzhik Mihhail Viktorovitš. Olen selle saidi omanik ja autor, kirjutasin kogu teoreetilise materjali ja ka arendasin veebipõhised harjutused ja kalkulaatorid, mida saate matemaatika õppimiseks kasutada.

Murrud. Murdude korrutamine ja jagamine.

Hariliku murru korrutamine murdosaga.

Tavaliste murdude korrutamiseks peate korrutama lugeja lugejaga (saame korrutise lugeja) ja nimetaja nimetajaga (saame korrutise nimetaja).

Murdude korrutamise valem:





Enne lugejate ja nimetajate korrutamist peate kontrollima, kas murdosa saab vähendada. Kui saate murdosa vähendada, on teil lihtsam edasisi arvutusi teha.

Märge! Siin pole vaja ühist nimetajat otsida!!

Hariliku murru jagamine murruga.

Hariliku murru jagamine murruga toimub järgmiselt: keerad teise murru ümber (st muudad lugejat ja nimetajat) ning pärast seda korrutatakse murrud.

Tavaliste murdude jagamise valem:





Murru korrutamine naturaalarvuga.

Märge! Murru korrutamisel naturaalarvuga korrutatakse murru lugeja meie naturaalarvuga ja murdosa nimetaja jäetakse samaks. Kui toote tulemuseks on vale murd, siis tõstke kindlasti esile kogu osa, muutes vale fraktsiooni segafraktsiooniks.



Naturaalarvudega murdude jagamine.

See pole nii hirmutav, kui tundub. Nagu liitmise puhul, teisendame täisarvu murdeks, mille nimetajas on üks. Näiteks:



Segamurdude korrutamine.

Murdude (segatud) korrutamise reeglid:

• teisendada segafraktsioonid valedeks fraktsioonideks;
• murdude lugejate ja nimetajate korrutamine;
• vähendada murdosa;
• Kui saate valemurru, teisendame valemurru segamurruks.

Märge! Segamurru korrutamiseks teise segamurruga peate need esmalt teisendama valede murdude kujule ja seejärel korrutama vastavalt tavaliste murdude korrutamise reeglile.



Teine viis murdosa korrutamiseks naturaalarvuga.

Võib-olla on mugavam kasutada teist meetodit hariliku murru arvuga korrutamiseks.

Märge! Murru korrutamiseks naturaalarvuga peate jagama murdosa nimetaja selle arvuga ja jätma lugeja muutmata.



Ülaltoodud näitest on selge, et seda võimalust on mugavam kasutada, kui murdosa nimetaja jagatakse ilma jäägita naturaalarvuga.

Mitmekorruselised murded.

Keskkoolis kohtab sageli kolmekorruselisi (või enamaid) murde. Näide:

Sellise murru tavapärasele kujule viimiseks kasutage jagamist kahe punktiga:



Märge! Murdude jagamisel on jagamise järjekord väga oluline. Olge ettevaatlik, siin on lihtne segadusse sattuda.

Märge, Näiteks:

Kui jagate ühe mis tahes murdosaga, on tulemuseks sama murd, ainult ümberpööratud:

Praktilised näpunäited murdude korrutamiseks ja jagamiseks:

1. Murdlausetega töötamisel on kõige olulisem täpsus ja tähelepanelikkus. Tehke kõik arvutused hoolikalt ja täpselt, kontsentreeritult ja selgelt. Parem on kirjutada oma mustandisse paar lisarida, kui eksida peastesse arvutustesse.

2. Erinevat tüüpi murrudega ülesannetes minge harilike murdude tüübi juurde.

3. Vähendame kõiki murde, kuni redutseerimine pole enam võimalik.

4. Teisendame mitmetasandilised murdavaldised tavalisteks, kasutades jagamist läbi 2 punkti.

• Under- ja under- Ümbertöödeldud laul "Kevadine tango" (Aeg tuleb - linnud lendavad lõunast) - muusika. Valeri Miljajev Ma ei kuulnud piisavalt, ma ei saanud aru, ma ei saanud sellest aru, selles mõttes, et ma ei arvanud, kirjutasin kõik verbid lahutamatult, ma ei teadnud eesliidet nedo. Juhtub, […]
• Lehekülge ei leitud Kolmandal lõplikul lugemisel võeti vastu valitsuse dokumentide pakett, mis näeb ette spetsiaalsete halduspiirkonnad(SAR). Euroopa Liidust lahkumise tulemusena ei kuulu Ühendkuningriik Euroopa käibemaksualasse ja […]
• Ühine juurdluskomitee ilmub sügisel Ühine juurdluskomitee ilmub sügisel Kõigi õiguskaitseorganite uurimine tuuakse neljandal katsel ühe katuse alla Juba 2014. aasta sügisel on Izvestija andmetel president Vladimir Putin [ …]
• Algoritmi patent Kuidas näeb välja algoritmi patent Kuidas algoritmi patent koostatakse Ettevalmistus tehnilised kirjeldused spetsiaalselt patenteerimise eesmärgil signaalide ja/või andmete salvestamise, töötlemise ja edastamise meetodid ei tekita tavaliselt erilisi raskusi ja […]
• MIDA ON OLULINE TEADA UUE PENSIONIDE EELNÕU KOHTA 12. detsember 1993 VENEMAA FÖDERATSIOONI PÕHISEADUS (võttes arvesse Vene Föderatsiooni seadustega tehtud muudatusi Vene Föderatsiooni põhiseaduse muudatuste kohta, 30. detsember 2008 N 6- FKZ, 30. detsember 2008 N 7-FKZ, […]
• Naljakad jamad naiste pensionist päevakangelasele, mehed päevakangelasele, mehed - kooris päevakangelasele, naised - pühendus pensionäridele, naised, humoorikas.Pensionäride võistlused tulevad huvitavad. Saatejuht : kallid sõbrad! Üks hetk! Sensatsioon! Ainult […]