Subtracting fractions with different examples. Adding Fractions

Note! Before writing your final answer, see if you can shorten the fraction you received.

Subtracting fractions with like denominators, examples:

Subtracting a proper fraction from one.

If it is necessary to subtract a fraction from a unit that is proper, the unit is converted to the form of an improper fraction, its denominator is equal to the denominator of the subtracted fraction.

An example of subtracting a proper fraction from one:

Denominator of the fraction to be subtracted = 7 , i.e., we represent one as an improper fraction 7/7 and subtract it according to the rule for subtracting fractions with like denominators.

Subtracting a proper fraction from a whole number.

Rules for subtracting fractions - correct from a whole number (natural number):

We convert given fractions that contain an integer part into improper ones. We get normal terms (it doesn’t matter if they are with different denominators), which we calculate according to the rules given above;
Next, we calculate the difference between the fractions that we received. As a result, we will almost find the answer;
We perform the reverse transformation, that is, we get rid of the improper fraction - we select the whole part in the fraction.

Subtract from a whole number correct fraction: Introducing natural number as a mixed number. Those. We take a unit in a natural number and convert it to the form of an improper fraction, the denominator being the same as that of the subtracted fraction.

Example of subtracting fractions:

In the example, we replaced one with the improper fraction 7/7 and instead of 3 we wrote down a mixed number and subtracted a fraction from the fractional part.

Subtracting fractions with different denominators.

Or, to put it another way, subtracting different fractions.

Rule for subtracting fractions with different denominators. In order to subtract fractions with different denominators, it is necessary, first, to reduce these fractions to the lowest common denominator (LCD), and only after this, perform the subtraction as with fractions with the same denominators.

The common denominator of several fractions is LCM (least common multiple) natural numbers that are the denominators of these fractions.

Attention! If in the final fraction the numerator and denominator have common factors, then the fraction must be reduced. An improper fraction is best represented as a mixed fraction. Leaving the subtraction result without reducing the fraction where possible is an incomplete solution to the example!

Procedure for subtracting fractions with different denominators.

find the LCM for all denominators;
put additional factors for all fractions;
multiply all numerators by an additional factor;
We write the resulting products into the numerator, signing the common denominator under all fractions;
subtract the numerators of fractions, signing the common denominator under the difference.

In the same way, addition and subtraction of fractions is carried out if there are letters in the numerator.

Subtracting fractions, examples:

Subtracting mixed fractions.

At subtracting mixed fractions (numbers) separately, the integer part is subtracted from the integer part, and the fractional part is subtracted from the fractional part.

The first option for subtracting mixed fractions.

If the fractional parts the same denominators and numerator of the fractional part of the minuend (we subtract it from it) ≥ numerator of the fractional part of the subtrahend (we subtract it).

For example:

The second option for subtracting mixed fractions.

When fractional parts different denominators. To begin with, we bring the fractional parts to a common denominator, and after that we subtract the whole part from the whole part, and the fractional part from the fractional part.

For example:

The third option for subtracting mixed fractions.

The fractional part of the minuend is less than the fractional part of the subtrahend.

Example:

Because Fractional parts have different denominators, which means, as in the second option, we first bring ordinary fractions to a common denominator.

The numerator of the fractional part of the minuend is less than the numerator of the fractional part of the subtrahend.3 < 14. This means we take a unit from the whole part and reduce this unit to the form of an improper fraction with the same denominator and numerator = 18.

In the numerator on the right side we write the sum of the numerators, then we open the brackets in the numerator on the right side, that is, we multiply everything and give similar ones. We do not open the parentheses in the denominator. It is customary to leave the product in the denominators. We get:

Fractions are regular numbers, they can also be added and subtracted. But because they have a denominator, they require more complex rules than for integers.

Let's consider the simplest case, when there are two fractions with the same denominators. Then:

To add fractions with the same denominators, you need to add their numerators and leave the denominator unchanged.

To subtract fractions with the same denominators, you need to subtract the numerator of the second from the numerator of the first fraction, and again leave the denominator unchanged.

Within each expression, the denominators of the fractions are equal. By definition of adding and subtracting fractions we get:

As you can see, it’s nothing complicated: we just add or subtract the numerators and that’s it.

But even in such simple actions, people manage to make mistakes. What is most often forgotten is that the denominator does not change. For example, when adding them, they also begin to add up, and this is fundamentally wrong.

Get rid of bad habit Adding the denominators is quite simple. Try the same thing when subtracting. As a result, the denominator will be zero, and the fraction will (suddenly!) lose its meaning.

Therefore, remember once and for all: when adding and subtracting, the denominator does not change!

Many people also make mistakes when adding several negative fractions. There is confusion with the signs: where to put a minus and where to put a plus.

This problem is also very easy to solve. It is enough to remember that the minus before the sign of a fraction can always be transferred to the numerator - and vice versa. And of course, don’t forget two simple rules:

Plus by minus gives minus;
Two negatives make an affirmative.

Let's look at all this with specific examples:

Task. Find the meaning of the expression:

In the first case, everything is simple, but in the second, let’s add minuses to the numerators of the fractions:

What to do if the denominators are different

You cannot add fractions with different denominators directly. At least, this method is unknown to me. However, the original fractions can always be rewritten so that the denominators become the same.

There are many ways to convert fractions. Three of them are discussed in the lesson “Reducing fractions to a common denominator”, so we will not dwell on them here. Let's look at some examples:

Task. Find the meaning of the expression:

In the first case, we reduce the fractions to a common denominator using the “criss-cross” method. In the second we will look for the NOC. Note that 6 = 2 · 3; 9 = 3 · 3. The last factors in these expansions are equal, and the first ones are relatively prime. Therefore, LCM(6, 9) = 2 3 3 = 18.

What to do if a fraction has an integer part

I can please you: different denominators in fractions are not the biggest evil. Much more errors occur when the whole part is highlighted in the addend fractions.

Of course, there are own addition and subtraction algorithms for such fractions, but they are quite complex and require a long study. Better use simple diagram, given below:

Convert all fractions containing an integer part to improper ones. We obtain normal terms (even with different denominators), which are calculated according to the rules discussed above;
Actually, calculate the sum or difference of the resulting fractions. As a result, we will practically find the answer;
If this is all that was required in the problem, we perform the inverse transformation, i.e. We get rid of an improper fraction by highlighting the whole part.

The rules for moving to improper fractions and highlighting the whole part are described in detail in the lesson “What is a numerical fraction”. If you don’t remember, be sure to repeat it. Examples:

Task. Find the meaning of the expression:

Everything is simple here. The denominators inside each expression are equal, so all that remains is to convert all fractions to improper ones and count. We have:

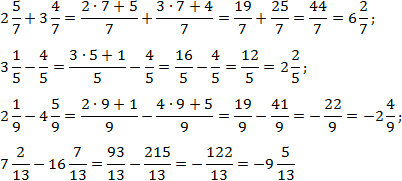
To simplify the calculations, I have skipped some obvious steps in the last examples.

A small note on the last two examples, where fractions with the highlighted ones are subtracted whole part. The minus before the second fraction means that the entire fraction is subtracted, and not just its whole part.

Re-read this sentence again, look at the examples - and think about it. This is where beginners admit great amount errors. They love to give such tasks to tests. You will also encounter them several times in the tests for this lesson, which will be published shortly.

Summary: general calculation scheme

In conclusion I will give general algorithm, which will help you find the sum or difference of two or more fractions:

If one or more fractions have an integer part, convert these fractions to improper ones;
Bring all the fractions to a common denominator in any way convenient for you (unless, of course, the writers of the problems did this);
Add or subtract the resulting numbers according to the rules for adding and subtracting fractions with like denominators;
If possible, shorten the result. If the fraction is incorrect, select the whole part.

Remember that it is better to highlight the whole part at the very end of the task, immediately before writing down the answer.

The next action that can be performed with ordinary fractions is subtraction. In this material, we will look at how to correctly calculate the difference between fractions with like and unlike denominators, how to subtract a fraction from a natural number and vice versa. All examples will be illustrated with problems. Let us clarify in advance that we will only examine cases where the difference of fractions results in a positive number.

Yandex.RTB R-A-339285-1

How to find the difference between fractions with like denominators

Let's start right away with a clear example: let's say we have an apple that has been divided into eight parts. Let's leave five parts on the plate and take two of them. This action can be written like this:

As a result, we have 3 eighths left, since 5 − 2 = 3. It turns out that 5 8 - 2 8 = 3 8.

Thereby simple example We saw exactly how the subtraction rule works for fractions whose denominators are the same. Let's formulate it.

Definition 1

To find the difference between fractions with like denominators, you need to subtract the numerator of the other from the numerator of one, and leave the denominator the same. This rule can be written as a b - c b = a - c b.

We will use this formula in the future.

Let's take specific examples.

Example 1

Subtract the common fraction 17 15 from the fraction 24 15.

Solution

We see that these fractions have the same denominators. So all we need to do is subtract 17 from 24. We get 7 and add the denominator to it, we get 7 15.

Our calculations can be written as follows: 24 15 - 17 15 = 24 - 17 15 = 7 15

If necessary, you can shorten a complex fraction or select an entire part from an improper fraction to make counting more convenient.

Example 2

Find the difference 37 12 - 15 12.

Solution

Let's use the formula described above and calculate: 37 12 - 15 12 = 37 - 15 12 = 22 12

It is easy to notice that the numerator and denominator can be divided by 2 (we already talked about this earlier when we examined the signs of divisibility). Shortening the answer, we get 11 6. This improper fraction, from which we will select the whole part: 11 6 = 1 5 6 .

How to find the difference of fractions with different denominators

This mathematical operation can be reduced to what we have already described above. To do this, we simply reduce the necessary fractions to the same denominator. Let's formulate a definition:

Definition 2

To find the difference between fractions that have different denominators, you need to reduce them to the same denominator and find the difference between the numerators.

Let's look at an example of how this is done.

Example 3

Subtract the fraction 1 15 from 2 9.

Solution

The denominators are different, and you need to reduce them to the smallest overall value. In this case, the LCM is 45. The first fraction requires an additional factor of 5, and the second - 3.

Let's calculate: 2 9 = 2 5 9 5 = 10 45 1 15 = 1 3 15 3 = 3 45

We have two fractions with the same denominator, and now we can easily find their difference using the algorithm described earlier: 10 45 - 3 45 = 10 - 3 45 = 7 45

A short summary of the solution looks like this: 2 9 - 1 15 = 10 45 - 3 45 = 10 - 3 45 = 7 45.

Do not neglect reducing the result or separating an entire part from it, if necessary. In this example we don't need to do that.

Example 4

Find the difference 19 9 - 7 36.

Solution

Let's reduce the fractions indicated in the condition to the lowest common denominator 36 and get 76 9 and 7 36, respectively.

We calculate the answer: 76 36 - 7 36 = 76 - 7 36 = 69 36

The result can be reduced by 3 and get 23 12. The numerator is greater than the denominator, which means we can select the whole part. The final answer is 1 11 12.

A short summary of the entire solution is 19 9 - 7 36 = 1 11 12.

How to subtract a natural number from a common fraction

This action can also be easily reduced to simple subtraction of ordinary fractions. This can be done by representing a natural number as a fraction. Let's show it with an example.

Example 5

Find the difference 83 21 – 3 .

Solution

3 is the same as 3 1. Then you can calculate it like this: 83 21 - 3 = 20 21.

If the condition requires subtracting an integer from an improper fraction, it is more convenient to first separate the integer from it by writing it as a mixed number. Then the previous example can be solved differently.

From the fraction 83 21, when separating the whole part, the result is 83 21 = 3 20 21.

Now let's just subtract 3 from it: 3 20 21 - 3 = 20 21.

How to subtract a fraction from a natural number

This action is done similarly to the previous one: we rewrite the natural number as a fraction, bring both to a single denominator and find the difference. Let's illustrate this with an example.

Example 6

Find the difference: 7 - 5 3 .

Solution

Let's make 7 a fraction 7 1. We do the subtraction and transform the final result, separating the whole part from it: 7 - 5 3 = 5 1 3.

There is another way to make calculations. It has some advantages that can be used in cases where the numerators and denominators of the fractions in the problem are large numbers.

Definition 3

If the fraction that needs to be subtracted is proper, then the natural number from which we are subtracting must be represented as the sum of two numbers, one of which is equal to 1. After this, you need to subtract the desired fraction from unity and get the answer.

Example 7

Calculate the difference 1 065 - 13 62.

Solution

The fraction to be subtracted is a proper fraction because its numerator is less than its denominator. Therefore, we need to subtract one from 1065 and subtract the desired fraction from it: 1065 - 13 62 = (1064 + 1) - 13 62

Now we need to find the answer. Using the properties of subtraction, the resulting expression can be written as 1064 + 1 - 13 62. Let's calculate the difference in brackets. To do this, let's imagine unit as a fraction 1 1.

It turns out that 1 - 13 62 = 1 1 - 13 62 = 62 62 - 13 62 = 49 62.

Now let's remember about 1064 and formulate the answer: 1064 49 62.

We use the old method to prove that it is less convenient. These are the calculations we would come up with:

1065 - 13 62 = 1065 1 - 13 62 = 1065 62 1 62 - 13 62 = 66030 62 - 13 62 = = 66030 - 13 62 = 66017 62 = 1064 4 6

The answer is the same, but the calculations are obviously more cumbersome.

We looked at the case where we need to subtract a proper fraction. If it is incorrect, we replace it with a mixed number and subtract according to familiar rules.

Example 8

Calculate the difference 644 - 73 5.

Solution

The second fraction is an improper fraction, and the whole part must be separated from it.

Now we calculate similarly to the previous example: 630 - 3 5 = (629 + 1) - 3 5 = 629 + 1 - 3 5 = 629 + 2 5 = 629 2 5

Properties of subtraction when working with fractions

The properties that subtraction of natural numbers have also apply to cases of subtraction of ordinary fractions. Let's look at how to use them when solving examples.

Example 9

Find the difference 24 4 - 3 2 - 5 6.

Solution

We have already solved similar examples when we looked at subtracting a sum from a number, so we follow the already known algorithm. First, let's calculate the difference 25 4 - 3 2, and then subtract the last fraction from it:

25 4 - 3 2 = 24 4 - 6 4 = 19 4 19 4 - 5 6 = 57 12 - 10 12 = 47 12

Let's transform the answer by separating the whole part from it. Result - 3 11 12.

A short summary of the entire solution:

25 4 - 3 2 - 5 6 = 25 4 - 3 2 - 5 6 = 25 4 - 6 4 - 5 6 = = 19 4 - 5 6 = 57 12 - 10 12 = 47 12 = 3 11 12

If the expression contains both fractions and natural numbers, it is recommended to group them by type when calculating.

Example 10

Find the difference 98 + 17 20 - 5 + 3 5.

Solution

Knowing the basic properties of subtraction and addition, we can group numbers as follows: 98 + 17 20 - 5 + 3 5 = 98 + 17 20 - 5 - 3 5 = 98 - 5 + 17 20 - 3 5

Let's complete the calculations: 98 - 5 + 17 20 - 3 5 = 93 + 17 20 - 12 20 = 93 + 5 20 = 93 + 1 4 = 93 1 4

If you notice an error in the text, please highlight it and press Ctrl+Enter

Your child brought homework from school and you don't know how to solve it? Then this mini lesson is for you!

How to add decimals

It is more convenient to add decimal fractions in a column. To perform addition decimals, you must adhere to one simple rule:

The place must be under the place, the comma under the comma.

As you can see in the example, the whole units are located under each other, the tenths and hundredths digits are located under each other. Now we add the numbers, ignoring the comma. What to do with the comma? The comma is moved to the place where it stood in the integer category.

Adding fractions with equal denominators

To perform addition with a common denominator, you need to keep the denominator unchanged, find the sum of the numerators and get a fraction that will be the total sum.

Adding fractions with different denominators using the common multiple method

The first thing you need to pay attention to is the denominators. The denominators are different, are they not divisible by each other, are they prime numbers. First we need to bring it to one common denominator; there are several ways to do this:

1/3 + 3/4 = 13/12, to solve this example we need to find the least common multiple (LCM) that will be divisible by 2 denominators. To denote the smallest multiple of a and b – LCM (a;b). In this example LCM (3;4)=12. We check: 12:3=4; 12:4=3.
We multiply the factors and add the resulting numbers, we get 13/12 - an improper fraction.

In order to convert an improper fraction into a proper one, divide the numerator by the denominator, we get the integer 1, the remainder 1 is the numerator and 12 is the denominator.

Adding fractions using the cross-cross multiplication method

To add fractions with different denominators, there is another method using the “cross to cross” formula. This is a guaranteed way to equalize the denominators; to do this, you need to multiply the numerators with the denominator of one fraction and vice versa. If you're just on initial stage studying fractions, then this method is the simplest and most accurate way to get the correct result when adding fractions with different denominators.

Adding and subtracting fractions with like denominators
Adding and subtracting fractions with different denominators
Concept of NOC
Reducing fractions to the same denominator
How to add a whole number and a fraction

1 Adding and subtracting fractions with like denominators

To add fractions with the same denominators, you need to add their numerators, but leave the denominator the same, for example:

To subtract fractions with the same denominators, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator the same, for example:

To add mixed fractions, you need to separately add their whole parts, and then add their fractional parts, and write the result as a mixed fraction,

If, when adding fractional parts, you get an improper fraction, select the whole part from it and add it to the whole part, for example:

2 Adding and subtracting fractions with different denominators

In order to add or subtract fractions with different denominators, you must first reduce them to the same denominator, and then proceed as indicated at the beginning of this article. The common denominator of several fractions is the LCM (least common multiple). For the numerator of each fraction, additional factors are found by dividing the LCM by the denominator of this fraction. We will look at an example later, after we understand what an NOC is.

3 Least common multiple (LCM)

The least common multiple of two numbers (LCM) is the smallest natural number that is divisible by both numbers without leaving a remainder. Sometimes the NOC can be selected orally, but more often, especially when working with large numbers, you have to find the LOC in writing using the following algorithm:

In order to find the LCM of several numbers, you need:

Factor these numbers into prime factors
Take the largest expansion and write these numbers as a product
Select in other decompositions the numbers that do not appear in the largest decomposition (or occur fewer times in it), and add them to the product.
Multiply all the numbers in the product, this will be the LCM.

For example, let's find the LCM of the numbers 28 and 21:

4Reducing fractions to the same denominator

Let's return to adding fractions with different denominators.

When we reduce fractions to the same denominator, equal to the LCM of both denominators, we must multiply the numerators of these fractions by additional multipliers. You can find them by dividing the LCM by the denominator of the corresponding fraction, for example:

Thus, to reduce fractions to the same exponent, you must first find the LCM (that is, smallest number, which is divisible by both denominators) of the denominators of these fractions, then add additional factors to the numerators of the fractions. You can find them by dividing the common denominator (CLD) by the denominator of the corresponding fraction. Then you need to multiply the numerator of each fraction by an additional factor, and put the LCM as the denominator.

5How to add a whole number and a fraction

In order to add a whole number and a fraction, you just need to add this number before the fraction, and you get mixed fraction, For example.