Õigete ja ebaõigete ratsionaalsete murdude integreerimine. Ratsionaalfunktsioonide integreerimine ja määramata koefitsientide meetod

Murd-ratsionaalfunktsiooni integreerimine.
Ebakindla koefitsiendi meetod

Jätkame tööd murdude integreerimisega. Oleme õppetunnis juba vaadanud mõnda tüüpi murdude integraale ja seda õppetundi võib teatud mõttes pidada jätkuks. Materjali edukaks mõistmiseks on vaja elementaarseid integreerimisoskusi, nii et kui olete just integraalide õppimist alustanud, st olete algaja, peate alustama artiklist Määramatu integraal. Näited lahendustest.

Kummalisel kombel hakkame nüüd tegelema mitte niivõrd integraalide leidmisega, vaid... lineaarvõrrandisüsteemide lahendamisega. Sellega seoses kiiresti Soovitan tunnis osaleda, nimelt pead olema hästi kursis asendusmeetoditega (“kool” meetod ja süsteemivõrrandite terminipõhise liitmise (lahutamise) meetod).

Mis on murdosaline ratsionaalne funktsioon? Lihtsate sõnadega, murdratsionaalfunktsioon on murd, mille lugeja ja nimetaja sisaldavad polünoome või polünoomide korrutisi. Pealegi on fraktsioonid keerukamad kui artiklis käsitletud Mõnede murdude integreerimine.

Õige murd-ratsionaalfunktsiooni integreerimine

Kohe näide ja tüüpiline algoritm murd-ratsionaalfunktsiooni integraali lahendamiseks.

Näide 1

Samm 1. Esimene asi, mida me ALATI teeme murdosalise ratsionaalse funktsiooni integraali lahendamisel, on selgitada järgmine küsimus: kas murd on õige? See samm sooritatakse suuliselt ja nüüd selgitan, kuidas:

Kõigepealt vaatame lugejat ja saame teada vanem kraad polünoom:

Lugeja juhtjõud on kaks.

Nüüd vaatame nimetajat ja saame teada vanem kraad nimetaja. Ilmselge viis on avada sulud ja tuua sarnased terminid, kuid saate seda teha ka lihtsamalt iga leida sulgudes kõrgeim kraad

ja mõtteliselt korrutada: - seega on nimetaja kõrgeim aste võrdne kolmega. On üsna ilmne, et kui me sulud reaalselt avame, ei saa me kraadi võrra suuremat kui kolm.

Järeldus: Lugeja peakraad RANGELT on väiksem kui nimetaja suurim võimsus, mis tähendab, et murd on õige.

Kui selles näites sisaldaks lugeja polünoomi 3, 4, 5 jne. kraadi, siis oleks murdosa vale.

Nüüd käsitleme ainult õigeid murdosalisi ratsionaalseid funktsioone. Juhtumit, mil lugeja aste on nimetaja astmest suurem või sellega võrdne, arutatakse tunni lõpus.

2. samm. Faktoriseerime nimetaja. Vaatame oma nimetajat:

Üldiselt on see juba tegurite tulemus, kuid sellegipoolest küsime endalt: kas on võimalik midagi muud laiendada? Piinamise objektiks on kahtlemata ruudukujuline kolmik. Otsustame ruutvõrrand:

Diskriminant on suurem kui null, mis tähendab, et trinoomi saab tõesti faktoriseerida:

Üldreegel: KÕIK, mida VÕIB nimetajas arvesse võtta – me arvestame selle

Alustame lahenduse sõnastamist:

3. samm. Kasutades määramatute koefitsientide meetodit, laiendame integrandi liht(elementaar)murdude summaks. Nüüd saab asi selgemaks.

Vaatame meie integrandi funktsiooni:

Ja teate, millegipärast tekib intuitiivne mõte, et oleks tore muuta meie suur murd mitmeks väikeseks. Näiteks nii:

Tekib küsimus, kas seda on üldse võimalik teha? Hingame kergendatult, vastav teoreem matemaatiline analüüs kinnitab – SEE ON VÕIMALIK. Selline lagunemine on olemas ja ainulaadne.

On ainult üks saak, tõenäosus on selline Hüvasti Me ei tea, sellest ka nimi – määramatute koefitsientide meetod.

Nagu arvasite, on järgnevad kehaliigutused sellised, ärge naerge! eesmärk on lihtsalt neid TUNNISTADA – et teada saada, millega nad on võrdsed.

Olge ettevaatlik, ma selgitan üksikasjalikult ainult üks kord!

Niisiis, alustame tantsimist:

Vasakul pool taandame avaldise ühiseks nimetajaks:

Nüüd saame nimetajatest ohutult lahti saada (kuna need on samad):

Vasakul küljel avame sulud, kuid ärge puudutage praegu tundmatuid koefitsiente:

Samal ajal kordame kooli reegel polünoomide korrutamine. Kui olin õpetaja, õppisin seda reeglit sirge näoga hääldama: Polünoomi polünoomiga korrutamiseks peate korrutama ühe polünoomi iga liikme teise polünoomi iga liikmega.

Selge selgituse seisukohalt on parem panna koefitsiendid sulgudesse (kuigi ma isiklikult ei tee seda kunagi aja säästmiseks):

Koostame lineaarvõrrandisüsteemi.
Kõigepealt otsime kõrgemaid kraade:

Ja me kirjutame vastavad koefitsiendid süsteemi esimesse võrrandisse:

Jäta hästi meelde järgmine punkt. Mis juhtuks, kui paremal pool s-d üldse poleks? Ütleme, kas see näitaks lihtsalt ilma ruuduta? Sel juhul oleks süsteemi võrrandis vaja paremale panna null: . Miks null? Aga sellepärast, et paremal pool saab alati määrata selle sama ruudu nulliga: Kui paremal pool pole muutujaid ja/või vaba liiget, siis paneme süsteemi vastavate võrrandite paremale küljele nullid.

Kirjutame vastavad koefitsiendid süsteemi teise võrrandisse:

Ja lõpuks, mineraalvesi, valime vabaliikmed.

Ee...ma tegin nalja. Nali naljaks – matemaatika on tõsine teadus. Meie instituudirühmas ei naernud keegi, kui abiprofessor ütles, et ta ajab terminid mööda arvurida laiali ja valib neist suurimad. Olgem tõsised. Kuigi... kes selle tunni lõpuni elab, naeratab ikka vaikselt.

Süsteem on valmis:

Lahendame süsteemi:

(1) Esimesest võrrandist väljendame ja asendame selle süsteemi 2. ja 3. võrrandiga. Tegelikult oli võimalik väljendada (või mõnda muud tähte) teisest võrrandist, kuid sel juhul on kasulik seda väljendada 1. võrrandist, kuna väikseim koefitsient.

(2) Esitame sarnased terminid 2. ja 3. võrrandis.

(3) Liidame 2. ja 3. võrrandi liikme kaupa, saades võrdsuse , millest järeldub, et

(4) Asendame teise (või kolmanda) võrrandiga, kust me selle leiame

(5) Asendage ja esimesse võrrandisse, saades .

Kui teil on raskusi süsteemi lahendamise meetoditega, harjutage neid tunnis. Kuidas lahendada lineaarvõrrandisüsteemi?

Pärast süsteemi lahendamist on alati kasulik kontrollida - asendada leitud väärtused iga süsteemi võrrandit, mille tulemusena peaks kõik "koonduma".

Peaaegu kohal. Leiti koefitsiendid ja:

Valmis töö peaks välja nägema umbes selline:

Nagu näha, oli ülesande peamiseks raskuseks lineaarvõrrandisüsteemi koostamine (õigesti!) ja (õigesti!) lahendamine. Ja viimases etapis pole kõik nii keeruline: kasutame lineaarsuse omadusi määramatu integraal ja integreerida. Pange tähele, et kõigi kolme integraali all on meil "tasuta" keeruline funktsioon, Rääkisin selle klassis integreerimise funktsioonidest Muutuja muutmise meetod määramata integraalis.

Kontrollige: eristage vastust:

Saadud on algne integrandi funktsioon, mis tähendab, et integraal on leitud õigesti.
Kontrollimise käigus pidime avaldise taandada ühisele nimetajale ja see pole juhuslik. Määramatute koefitsientide meetod ja avaldise taandamine ühiseks nimetajaks on vastastikku pöördtoimingud.

Näide 2

Leidke määramatu integraal.

Tuleme tagasi esimese näite murdosa juurde: . Lihtne on märgata, et nimetajas on kõik tegurid ERINEVAD. Tekib küsimus, mida teha, kui on antud näiteks järgmine murd: ? Siin on nimetajas kraadid ehk matemaatiliselt mitmekordsed. Lisaks on ruuttrinoom, mida ei saa faktoriseerida (lihtne on kontrollida, et võrrandi diskriminant on negatiivne, seega ei saa trinoomi faktoriseerida). Mida teha? Laiendus elementaarmurdude summaks näeb välja umbes selline mille tipus on tundmatud koefitsiendid või midagi muud?

Näide 3

Tutvustage funktsiooni

Samm 1. Kontrollime, kas meil on õige murd
Peamine lugeja: 2
Nimetaja kõrgeim aste: 8
, mis tähendab, et murd on õige.

2. samm. Kas nimetajas on võimalik midagi arvesse võtta? Ilmselgelt mitte, kõik on juba paika pandud. Ruuttrinoomi ei saa ülaltoodud põhjustel tooteks laiendada. Kapuuts. Vähem tööd.

3. samm. Kujutame ette murdosaline ratsionaalne funktsioon elementaarmurdude summana.
Sel juhul on laiendusel järgmine vorm:

Vaatame oma nimetajat:
Murd-ratsionaalfunktsiooni jagamisel elementaarmurdude summaks saab eristada kolme põhipunkti:

1) Kui nimetaja sisaldab "üksik" tegurit esimesele astmele (meie puhul), siis paneme ülaossa määramatu koefitsiendi (meie puhul). Näited nr 1, 2 koosnesid ainult sellistest “üksikutest” teguritest.

2) Kui nimetajal on mitmekordne kordaja, siis peate selle lagundama järgmiselt:
- see tähendab, et läbige järjestikku kõik "X" astmed esimesest n-nda astmeni. Meie näites on kaks mitut tegurit: ja , vaadake uuesti minu antud laiendust ja veenduge, et neid laiendatakse täpselt selle reegli järgi.

3) Kui nimetaja sisaldab teise astme lagunematut polünoomi (meie puhul), siis tuleb lugejas lagunemisel kirjutada lineaarne funktsioon ebakindlate koefitsientidega (meie puhul ebakindlate koefitsientidega ja ).

Tegelikult on veel üks neljas juhtum, kuid ma vaikin sellest, kuna praktikas on see äärmiselt haruldane.

Näide 4

Tutvustage funktsiooni tundmatute koefitsientidega elementaarmurdude summana.

See on näide sõltumatu otsus. Täislahendus ja vastus tunni lõpus.
Järgige algoritmi rangelt!

Kui mõistate põhimõtteid, mille järgi peate murdosa-ratsionaalfunktsiooni summaks laiendama, saate läbi närida peaaegu iga vaadeldava tüübi integraali.

Näide 5

Leidke määramatu integraal.

Samm 1. Ilmselt on murd õige:

2. samm. Kas nimetajas on võimalik midagi arvesse võtta? Saab. Siin on kuubikute summa . Korrutage nimetaja lühendatud korrutamisvalemi abil

3. samm. Määramatute koefitsientide meetodit kasutades laiendame integrandi elementaarmurdude summaks:

Pange tähele, et polünoomi ei saa faktoriseerida (kontrollige, et diskriminant oleks negatiivne), nii et ülaossa paneme tundmatute koefitsientidega lineaarse funktsiooni, mitte ainult ühe tähe.

Toome murdosa ühise nimetaja juurde:

Koostame ja lahendame süsteemi:

(1) Avaldame esimesest võrrandist ja asendame selle süsteemi teise võrrandiga (see on kõige ratsionaalsem viis).

(2) Esitame sarnased terminid teises võrrandis.

(3) Liidame liikme kaupa süsteemi teise ja kolmanda võrrandi.

Kõik edasised arvutused tehakse põhimõtteliselt suuliselt, kuna süsteem on lihtne.

(1) Murdude summa kirjutame üles vastavalt leitud koefitsientidele.

(2) Kasutame määramatu integraali lineaarsusomadusi. Mis juhtus teises integraalis? Selle meetodiga saate tutvuda õppetunni viimases lõigus. Mõnede murdude integreerimine.

(3) Taaskord kasutame lineaarsuse omadusi. Kolmandas integraalis hakkame eraldama tervet ruutu (tunni eelviimane lõik Mõnede murdude integreerimine).

(4) Võtame teise integraali, kolmandas valime täisruudu.

(5) Võtke kolmas integraal. Valmis.

Ratsionaalfunktsioon on murdosa vormist, mille lugejaks ja nimetajaks on polünoomid või polünoomide korrutised.

Näide 1. 2. samm.

.

Korrutame määramata koefitsiendid polünoomidega, mis ei ole selles üksikmurrus, kuid on teistes saadud murdudes:

Avame sulud ja võrdsustame algse integrandi lugeja saadud avaldisega:

Võrdsuse mõlemal poolel otsime termineid, millel on samad x astmed, ja koostame nendest võrrandisüsteemi:

.

Tühistame kõik x-id ja saame samaväärse võrrandisüsteemi:

.

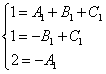Seega integrandi lõplik laiendamine summaks lihtmurrud:

.

Näide 2. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

.

Nüüd hakkame otsima ebakindlaid koefitsiente. Selleks võrdsustame funktsiooniavaldises oleva algse murru lugeja avaldise lugejaga, mis saadakse pärast murdude summa taandamist ühiseks nimetajaks:

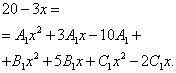
Nüüd peate looma ja lahendama võrrandisüsteemi. Selleks võrdsustame muutuja koefitsiendid vastava astmega funktsiooni algse avaldise lugejas ja sarnased koefitsiendid eelmises etapis saadud avaldises:

Lahendame saadud süsteemi:

Niisiis, siit

.

Näide 3. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

Hakkame otsima ebakindlaid koefitsiente. Selleks võrdsustame funktsiooniavaldises oleva algse murru lugeja avaldise lugejaga, mis saadakse pärast murdude summa taandamist ühiseks nimetajaks:

Nagu eelmistes näidetes, koostame võrrandisüsteemi:

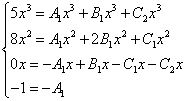
Vähendame x-e ja saame samaväärse võrrandisüsteemi:

Süsteemi lahendades saame ebakindlate koefitsientide järgmised väärtused:

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

.

Näide 4. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

.

Teame juba varasematest näidetest, kuidas võrdsustada algmurru lugejat lugejas oleva avaldisega, mis on saadud pärast murdarvu lammutamist lihtmurdude summaks ja selle summa viimist ühisnimetajasse. Seetõttu esitame lihtsalt kontrolli eesmärgil saadud võrrandisüsteemi:

Süsteemi lahendades saame ebakindlate koefitsientide järgmised väärtused:

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

Näide 5. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

.

Me taandame selle summa iseseisvalt ühiseks nimetajaks, võrdsustades selle avaldise lugeja algmurru lugejaga. Tulemuseks peaks olema järgmine võrrandisüsteem:

Süsteemi lahendades saame ebakindlate koefitsientide järgmised väärtused:

.

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

.

Näide 6. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

Teeme selle summaga samad toimingud nagu eelmistes näidetes. Tulemuseks peaks olema järgmine võrrandisüsteem:

Süsteemi lahendades saame ebakindlate koefitsientide järgmised väärtused:

.

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

.

Näide 7. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

.

Pärast teatud toiminguid saadud summaga tuleks saada järgmine võrrandisüsteem:

Süsteemi lahendades saame ebakindlate koefitsientide järgmised väärtused:

Saame integrandi lõpliku lagunemise lihtmurdude summaks:

.

Näide 8. 2. samm. Etapis 1 saime algse murdosa järgmise jaotuse lihtsate murdude summaks, mille lugejate koefitsiendid on määramata:

.

Teeme võrrandisüsteemi saamiseks mõned muudatused toimingutes, mis on juba automaatseks viidud. On kunstlik tehnika, mis mõnel juhul aitab vältida tarbetuid arvutusi. Viies murdude summa ühise nimetajani, saame ja võrdsustades selle avaldise lugeja algmurru lugejaga, saame.

Eelnevalt käsitlesime integratsiooni üldisi meetodeid. Selles ja järgmistes lõikudes räägime konkreetsete funktsiooniklasside integreerimisest käsitletud tehnikate abil.

Lihtsaimate ratsionaalsete funktsioonide integreerimine

Vaatleme vormi integraali \textstyle(\int R(x)\,dx), kus y=R(x) on ratsionaalne funktsioon. Suvalist ratsionaalset avaldist R(x) saab esitada kujul \frac(P(x))(Q(x)), kus P(x) ja Q(x) on polünoomid. Kui see murd on vale, st kui lugeja aste on suurem või võrdne nimetaja astmega, siis saab seda esitada polünoomi ( terve osa) ja õige murd. Seetõttu piisab õigete murdude integreerimisest.

Näitame, et selliste murdude integreerimine taandub integratsiooniks lihtmurrud, st vormi väljendid:

\mathsf(1))~\frac(A)(x-a);\quad \mathsf(2))~\frac(A)((x-a)^n);\quad \mathsf(3))~ \frac( Ax+B)(x^2+px+q);\quad \mathsf(4))~\frac(Ax+B)((x^2+px+q)^n).

Kus A,\,B,\,a,\,p,\,q on reaalarvud ja ruuttrinoomil x^2+px+q pole reaaljuuri. Tüübi 1) ja 2) avaldisi nimetatakse 1. tüübi murdudeks ning 3. ja 4. tüüpi avaldisi nimetatakse 2. tüüpi murdudeks.

Esimest tüüpi murdude integraalid arvutatakse otse

\begin(joondatud)\mathsf(1))&~\int\frac(A)(x-a)\,dx= A\ln|x-a|+C;\\ \mathsf(2))&~ \int\frac (A)((x-a)^n)\,dx= A\int(x-a)^(-n)\,dx= A\,\frac((x-a)^(-n+1))(-n+ 1 )+C~(n=2,3,4,\ldots). \end (joondatud)

Vaatleme teist tüüpi murdude integraalide arvutamist: \mathsf(3))~ \int\frac(Ax+B)(x^2+px+q)\,dx\,.

Esiteks märgime seda

\int\frac(dt)(t^2+a^2)= \frac(1)(a)\operaatorinimi(arctg)\frac(t)(a)+C,\qquad \int\frac(t\ ,dt)(t^2+a^2)= \frac(1)(2)\ln(t^2+a^2)+C.

Integraali 3) arvutamise taandamiseks nendele kahele integraalile teisendame ruutkolminoomi x^2+px+q, eraldades sellest täisruudu:

x^2+px+q= (\left(x+\frac(p)(2)\right)\^2+ \left(q-\frac{p^2}{4}\right)\!. !}

Kuna eeldusel, et sellel trinoomil pole tegelikke juuri, siis q-\frac(p^2)(4)>0 ja saame panna q-\frac(p^2)(4)=a^2. Asendamine x+\frac(p)(2)=t,~ dx=dt teisendab integraali 3) näidatud kahe integraali lineaarseks kombinatsiooniks:

\begin(joonatud)\int\frac(Ax+B)(x^2+px+q)\,dx&= \int\frac(A\!\left(t-\frac(p)(2)\right )+B)(t^2+a^2)\,dt= A\int\frac(t\,dt)(t^2+a^2)+ \left(B-\frac(Ap)(2 )\right)\!\int\frac(dt)(t^2+a^2)=\\ &=\frac(A)(2)\ln(t^2+a^2)+ \frac( 1)(a)\!\left(B-\frac(Ap)(2)\right)\!\ \operaatorinimi(arctg)\frac(t)(a)+C. \end (joondatud)

Lõplikus vastuses tuleb ainult (t) asendada x+\frac(p)(2) ja (a) \sqrt(q-\frac(p^2)(4)). Kuna t^2+a^2=x^2+px+q, siis

\int\frac(Ax+B)(x^2+px+q)\,dx= \frac(A)(2)\ln(x^2+px+q)+ \frac(B-\dfrac( Ap)(2))(\sqrt(q-\dfrac(p^2)(4))) \operaatorinimi(arctg)\frac(x+\dfrac(p)(2))(\sqrt(q-\dfrac (p^2) (4)))+C.

Kaaluge juhtumit \mathsf(4))~ \int\frac(Ax+B)((x^2+px+q)^n)\,dx.

Sarnaselt eelmisele juhul määrame x+\frac(p)(2)=t. Saame:

\int\frac(Ax+B)((x^2+px+q)^n)\,dx= A\int\frac(t\,dt)((t^2+a^2)^n) + \left(B-\frac(Ap)(2)\right)\! \int\frac(dt)((t^2+a^2)^n)\,.

Esimene tähtaeg arvutatakse järgmiselt:

A\int\frac(t\,dt)((t^2+a^2)^n)= \frac(A)(2)\int(t^2+a^2)^(-n)\ ,d(t^2+a^2)= \frac(A)(2)\frac((t^2+a^2)^(-n+1))(-n+1)= \frac( A)(2(1-n)(t^2+a^2)^(n-1))\,.

Teine integraal arvutatakse kordusvalemi abil.

Näide 1. Arvutame \int\frac(3x+2)(x^2+2x+3)\,dx.

Lahendus. Meil on: x^2+2x+3=(x+1)^2+2. Paneme x+1=t. Siis dx=dt ja 3x+2=3(t-1)+2=3t-1 ning seetõttu

\begin(joondatud)\int\frac(3x+2)(x^2+2x+3)\,dx&= \int\frac(3t-1)(t^2+2)\,dt= \frac( 3)(2)\int\frac(2t\,dt)(t^2+2)- \int\frac(dt)(t^2+(\sqrt(2))^2)=\\ &= \frac(3)(2)\ln(t^2+2)- \frac(1)(\sqrt(2))\operaatorinimi(arctg)\frac(t)(\sqrt(2))+C= \\ &=\frac(3)(2)\ln(x^2+2x+3)- \frac(1)(\sqrt(2))\operaatorinimi(arctg)\frac(x+1)(\ sqrt(2))+C. \end (joondatud)

Näide 2. Arvutame \int\frac(x+2)((x^2+6x+10)^2)\,dx.

Lahendus. Meil on: x^2+6x+10=(x+3)^2+1. Tutvustame uut muutujat, määrates x+3=t. Siis dt=dx ja x+2=t-1 . Asendades muutuja integraalimärgi all, saame:

\begin(joonatud)\int\frac(x+2)((x^2+6x+10)^2)\,dx&= \int\frac(t-1)((t^2+1)^2 )\,dt= \frac(1)(2)\int\frac(2t\,dt)((t^2+1)^2)-\int\frac(dt)((t^2+1) ^2)=\\ &=-\frac(1)(2(t^2+1))- \int\frac(dt)((t^2+1)^2)\,. \end (joondatud))

Paneme I_2=\int\frac(dt)((t^2+1)^2). Meil on:

I_2=\frac(1)(2)I_1+\frac(1)(2)\frac(t)(t^2+1), Aga I_1=\int\frac(dt)(t^2+1)= \operaatorinimi(arctg)t Seega I_2= \frac(1)(2)\operaatorinimi(arctg)t+ \frac(t)(2(t^2+1)).

Lõpuks saame:

\begin(joonatud)\int\frac(x+2)((x^2+6x+10)^2)\,dx&=-\frac(1)(2(t^2+1))-\frac (1)(2)\operaatorinimi(arctg)t-\frac(t)(2(t^2+1))=\\ &=-\frac(1)(2(x^2+6x+10) )- \frac(1)(2)\operaatorinimi(arctg)(x+3)- \frac(x+3)(2(x^2+6x+10))+C=\\ &=\frac( -x-4)(2(x^2+6x+10))-\frac(1)(2)\operaatorinimi(arctg)(x+3)+C \end(joondatud)

Õigete murdude integreerimine

Mõelge õigele murdosale R(x)=\frac(P(x))(Q(x)), kus Q(x) on n-astme polünoom. Üldisust kaotamata võib eeldada, et Q(x) juhtkoefitsient on võrdne 1-ga. Algebra kursusel on tõestatud, et sellist reaalkoefitsientidega polünoomi saab faktoriseerida reaalkoefitsientidega esimese ja teise astme teguriteks. :

Q(x)= (x-x_1)^(\alpha)\lpunktid (x-x_k)^(\beta) (x^2+p\,x+q)^(\gamma)\lpunktid (x^2) +r\,x+s)^(\delta).

kus x_1,\ldots,x_k on polünoomi Q(x) reaaljuured ja ruuttrinoomidel pole reaaljuuri. Võib tõestada, et siis R(x) esitatakse lihtmurdude summana kujul 1) -4):

\begin(joondatud)R(x)=&\frac(P(x))(Q(x))= \frac(A_1)((x-x_1)^(\alpha))+ \frac(A_2)( (x-x_1)^(\alpha-1))+\ldots+ \frac(A_(\alpha))(x-x_1)\,+\\ &+\,\ldots+ \frac(B_1)((x- x_k)^(\beta))+ \frac(B_2)((x-x_k)^(\beta-1))+\ldots+ \frac(B_(\beta))(x-x_k)+ \frac(M_1x+ N_1)((x^2+p\,x+q)^(\gamma))\,+\\ &+\,\ldots+ \frac(M_(\gamma)+ N_(\gamma))(x^ 2+ p\,x+s)+ \frac(E_1x+F_1)((x^2+rx+s)^(\delta))+\ldots+ \frac(E_(\delta)x+F_(\delta ))(x^2+rx+s)\, \end(joondatud)

kus nimetajate eksponendid vähenevad järjestikku \alpha-lt 1-le, ..., \beta-lt 1-le, \gamma-lt 1-le, ..., \deltalt 1-le ja A_1,\ldots,F_(\delta)- ebakindlad koefitsiendid. Nende koefitsientide leidmiseks tuleb nimetajatest lahti saada ja kahe polünoomi võrdsuse saamisel kasutada määramatute kordajate meetodit.

Teine võimalus koefitsientide määramiseks A_1,\ldots, A_(\alpha), \ldots, F_(\delta) põhineb muutuja x väärtuste asendamisel. Asendades pärast nimetajate elimineerimist võrrandist (1) saadud võrrandisse x asemel suvalise arvu, jõuame lineaarvõrrand nõutavate koefitsientide suhtes. Asendades vajaliku arvu selliseid muutuja osaväärtusi, saame võrrandisüsteemi koefitsientide leidmiseks. Kõige mugavam on muutuja privaatväärtusteks valida nimetaja juured (nii tegelikud kui ka komplekssed). Sel juhul kaovad peaaegu kõik võrdsuse (mis tähendab kahe polünoomi võrdsust) paremal poolel olevad terminid, mis teeb ülejäänud kordajate leidmise lihtsaks. Kompleksväärtuste asendamisel pidage meeles, et kaks kompleksarvu on võrdsed siis ja ainult siis, kui nende reaal- ja mõtteline osa on vastavalt võrdsed. Seetõttu saadakse igast kompleksarve sisaldavast võrrandist kaks võrrandit.

Pärast määramata koefitsientide leidmist jääb üle arvutada saadud lihtsamate murdude integraalid. Kuna lihtsaimate murdude integreerimisel, nagu nägime, saadakse ainult ratsionaalfunktsioonid, arktangensid ja logaritmid, siis mis tahes ratsionaalfunktsiooni integraali väljendatakse ratsionaalfunktsiooni, arctangentide ja logaritmide kaudu.

Näide 3. Arvutame korraliku ratsionaalse murru integraali \int\frac(6x+1)(x^2+2x-3)\,dx.

Lahendus. Faktoriseerime integrandi nimetaja:

x^2+2x-3=(x-1)(x+3).

Kirjutame välja integrandi ja esitame selle lihtmurdude summana:

\frac(6x+1)(x^2+2x-3)= \frac(A)(x-1)+\frac(B)(B+3)\,.

6x+1=A\cpunkt (x+3)+B\cpunkt (x-1)\,.

Koefitsientide leidmiseks kasutame osaväärtuste asendusmeetodit. Koefitsiendi A leidmiseks paneme x=1. Siis võrrandist (2) saame 7=4A, kust A=7/4. Koefitsiendi B leidmiseks paneme x=-3. Siis võrdsusest (2) saame -17=-4B, kust B=17/4.

Niisiis, \frac(6x+1)(x^2+2x-3)= \frac(7)(4)\cdot\frac(1)(x-1)+ \frac(17)(4)\cdot\frac (1) (x+3). Tähendab,

\int\frac(6x+1)(x^2+2x-3)\,dx= \frac(7)(4)\int\frac(dx)(x-1)+ \frac(17)(4 )\int\frac(dx)(x+3)= \frac(7)(4)\ln|x-1|+ \frac(17)(4)\ln|x+3|+C.

Näide 4. Arvutame \int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx.

Lahendus. Kirjutame välja integrandi ja esitame selle lihtmurdude summana. Nimetaja sisaldab tegurit x^2+2, millel pole pärisjuuri; see vastab murdosale 2. liigist: \frac(Ax+B)(x^2+2) kordaja (x-1)^2 vastab kahe esimest tüüpi murru summale: \frac(C)((x-1)^2)+ \frac(D)(x-1); lõpuks vastab tegur x+2 ühele 1. tüüpi \frac(E)(x+2) murdosale. Seega esitame integrandi funktsiooni nelja murdosa summana:

\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(Ax+B)(x^2+2 )+ \frac(C)((x-1)^2)+ \frac(D)(x-1)+ \frac(E)(x+2)\,.

\begin (joondatud) x^4+2x^2+8x+5&= (Ax+B)(x-1)^2(x+2)+ C(x^2+2)(x+2)\, +\\ &\phantom(=)+ D(x^2+2)(x-1)(x+2)+ E(x^2+2)(x-1)^2.\end(joondatud)

Integrandi nimetajal on kaks reaaljuurt: x=1 ja x=-2. Väärtuse x=1 asendamisel võrdsusega (4) saame 16=9C, millest leiame C=16/9. Asendades x=-2 saame 13=54E ja defineerime vastavalt E=13/54. Väärtuse x=i\,\sqrt(2) (polünoomi x^2+2 juur) asendamine võimaldab meil minna võrdusse

4-4+8\,i\,\sqrt(2)+5= (A\,i\,\sqrt(2)+B)\cdot (i\,\sqrt(2)-1)^2\ cdot (i\,\sqrt(2)+2).

See muundub järgmisele kujule:

(10A+2B)+(2A-5B)\sqrt(2)\,i= 5+8\sqrt(2)\,i, kust 10A+2B=5 ja (2A-5B)\sqrt(2)=8\sqrt(2).

Kahe muutujaga kahe võrrandisüsteemi lahendamine \begin(juhud)10A+2B=5,\\ 2A-5B=8,\end(juhtumid) leiame: A=\frac(41)(54),~ B=-\frac(35)(27).

Jääb kindlaks määrata koefitsiendi D väärtus. Selleks avame võrdsuses (4) olevad sulud, esitame sarnased terminid ja võrdleme seejärel x^4 koefitsiente. Saame:

A+D+E=1, see tähendab D=0.

Asendame koefitsientide leitud väärtused võrdsusega (3):

\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))= \frac(\drac(41)(54)\, x- \dfrac(35)(27))(x^2+2)+ \frac(16)(9)\frac(1)((x-1)^2)+ \frac(13)(54) \frac(1)(x+2)\,

\begin(joondatud)\int\frac(x^4+2x^2+8x+5)((x^2+2)(x-1)^2(x+2))\,dx&= \frac( 41)(54)\int\frac(x\,dx)(x^2+2)- \frac(35)(27)\int\frac(dx)(x^2+2)+ \frac(16) )(9) \int\frac(dx)((x-1)^2)+ \frac(13)(54)\int\frac(dx)(x+2)=\\ &=\frac(41 )(108)\ln(x^2+2)- \frac(35)(27\sqrt(2))\operaatorinimi(arctg)\frac(x)(\sqrt(2))- \frac(16) (9(x-1))+ \frac(13)(54) \ln|x+2|+C.\end(joondatud)

Vale murdude integreerimine

Oletame, et peame funktsiooni integreerima y=\frac(f(x))(g(x)), kus f(x) ja g(x) on polünoomid ja polünoomi f(x) aste on suurem või võrdne polünoomi g(x) astmega. Sel juhul peate kõigepealt valima kogu osa vale murd \frac(f(x))(g(x)), st kujutage seda kujul

\frac(f(x))(g(x))=s(x)+ \frac(r(x))(g(x))\,

kus s(x) on polünoom, mille aste on võrdne polünoomide f(x) ja g(x) astmete vahega ja \frac(r(x))(g(x))- õige murdosa.

Siis on meil \int\frac(f(x))(g(x))\,dx= \int s(x)\,dx+ \int\frac(r(x))(g(x))\,dx\, ..

Näide 5. Arvutame valemurru integraali \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx.

Lahendus. Meil on:

\begin(joonatud)g(x)&=(x-1)(x+2)(x-3)= x^3-2x^2-5x+6,\\ f(x)&=x^4 -4x^3+x^2+16x-11. \end (joondatud)

Kogu osa eraldamiseks jagage f(x) g(x)-ga: \frac(f(x))(g(x))= x-2+\frac(2x^2+1)(x^3-2x^2-5x+6)\,.

Tähendab, \int\frac(x^4-4x^3+x^2+16x-11)((x-1)(x+2)(x-3))\,dx= \int(x-2)dx+ \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx

Meil on: \int(x-2)dx=\frac(x^2)(2)-2x+C.

Integraali arvutamiseks \int\frac(2x^2+1)((x-1)(x+2)(x-3))\,dx Kasutatakse määramatute koefitsientide meetodit, nagu eespool. Pärast arvutusi, mille jätame lugeja hooleks, saame.

TEEMA: Integratsioon ratsionaalsed murded.

Tähelepanu! Uurides üht integreerimise põhimeetodit: ratsionaalsete murdude integreerimist, on rangete tõestuste tegemiseks vaja arvestada kompleksvaldkonna polünoomidega. Seetõttu on vajalik eelnevalt õppima mõned kompleksarvude omadused ja tehted nendega.

Lihtratsionaalsete murdude integreerimine.

Kui P(z) Ja K(z) on kompleksvaldkonnas polünoomid, siis on need ratsionaalsed murrud. Seda nimetatakse õige, kui kraad P(z) vähem kraadi K(z) , Ja vale, kui kraad R mitte vähem kui kraad K.

Iga vale murdosa võib esitada järgmiselt: ,

P(z) = Q(z) S(z) + R(z),

a R(z) – polünoom, mille aste on astmest väiksem K(z).

Seega taandub ratsionaalsete murdude integreerimine polünoomide, st astmefunktsioonide ja õigete murdude integreerimisele, kuna see on õige murd.

Definitsioon 5. Lihtsamad (või elementaar-) murrud on järgmist tüüpi murded:

1) , 2) , 3) , 4) .

Uurime, kuidas nad integreeruvad.

3) (uurinud varem).

Teoreem 5. Iga õiget murdu saab esitada lihtmurdude summana (ilma tõestuseta).

Järeldus 1. Kui on õige ratsionaalne murd ja kui polünoomi juurte hulgas on ainult lihtreaaljuured, siis murdu lihtmurdude summaks on ainult 1. tüüpi lihtmurrud:

Näide 1.

Järeldus 2. Kui on õige ratsionaalne murd ja kui polünoomi juurte hulgas on ainult mitu reaaljuurt, siis murdu lagundamisel lihtmurdude summaks on ainult 1. ja 2. tüübi lihtmurrud. :

Näide 2.

Järeldus 3. Kui on õige ratsionaalne murd ja kui polünoomi juurte hulgas on ainult lihtsad komplekssed konjugaatjuured, siis murdu lagundamisel lihtmurdude summaks on ainult 3. tüüpi lihtmurrud:

Näide 3.

Järeldus 4. Kui on korralik ratsionaalne murd ja kui polünoomi juurte hulgas on ainult mitu kompleksset konjugaatjuurt, siis murdu lagundamisel lihtmurdude summaks on ainult 3. ja 4. lihtmurrud. tüübid:

Tundmatute koefitsientide määramiseks antud laiendustes toimige järgmiselt. Tundmatuid koefitsiente sisaldava laienduse vasak ja parem pool korrutatakse kahe polünoomi võrdsusega. Sellest saadakse nõutavate koefitsientide võrrandid, kasutades:

1. võrdsus kehtib kõigi X väärtuste puhul (osalise väärtuse meetod). Sel juhul saadakse suvaline arv võrrandeid, millest mis tahes m võimaldab leida tundmatuid koefitsiente.

2. koefitsiendid langevad kokku X samade astmete korral (määramatute koefitsientide meetod). Sel juhul saadakse m - võrrandite süsteem m - tundmatutega, millest leitakse tundmatud koefitsiendid.

3. kombineeritud meetod.

Näide 5. Laienda murdosa kõige lihtsamatele.

Lahendus:

Leiame koefitsiendid A ja B.

1. meetod – eraväärtuse meetod:

2. meetod – määramata koefitsientide meetod:

Vastus:

Ratsionaalsete murdude integreerimine.

6. teoreem. Mis tahes ratsionaalse murru määramatu integraal mis tahes intervallil, mille nimetaja ei ole võrdne nulliga, on olemas ja seda väljendatakse elementaarfunktsioonide, nimelt ratsionaalsete murdude, logaritmide ja arctangentide kaudu.

Tõestus.

Kujutagem ette ratsionaalset murdosa kujul: . Sel juhul on viimane liige korralik murd ja teoreemi 5 kohaselt võib seda esitada lihtmurdude lineaarse kombinatsioonina. Seega taandatakse ratsionaalse murru integreerimine polünoomi integreerimiseks S(x) ja lihtmurrud, mille antiderivaadid, nagu näidatud, on teoreemis näidatud kujul.

Kommenteeri. Peamine raskus on sel juhul nimetaja lagunemine teguriteks, see tähendab kõigi selle juurte otsimine.

Näide 1. Leidke integraal