Sobimatute murdude vähendamine. Veebikalkulaator algebraliste murdude vähendamiseks koos üksikasjaliku lahendusega võimaldab teil murdu vähendada ja vale murdu õigeks murdeks teisendada

Kui meil on vaja 497 jagada 4-ga, siis jagamisel näeme, et 497 ei jagu 4-ga ühtlaselt, s.t. ülejäänud osa jääb alles. Sellistel juhtudel öeldakse, et see on lõpetatud jäägiga jagamine ja lahendus kirjutatakse järgmiselt:
497: 4 = 124 (1 jääk).

Võrdsuse vasakul küljel olevaid jagamise komponente nimetatakse samadeks, mis ilma jäägita jagamisel: 497 - dividend, 4 - jagaja. Nimetatakse jagamise tulemus jäägiga jagamisel puudulik privaatne. Meie puhul on see number 124. Ja lõpuks, viimane komponent, mis ei ole tavalises jaotuses, on ülejäänud osa. Juhtudel, kui jääki pole, öeldakse, et üks arv jagatakse teisega jäljetult või täielikult. Arvatakse, et sellise jagamise korral on jääk null. Meie puhul on jääk 1.

Ülejäänud osa on alati väiksem kui jagaja.

Jagamist saab kontrollida korrutamisega. Kui on näiteks võrdsus 64: 32 = 2, siis saab kontrollida järgmiselt: 64 = 32 * 2.

Sageli juhtudel, kui tehakse jäägiga jagamine, on mugav kasutada võrdsust
a = b * n + r,
kus a on dividend, b on jagaja, n on osajagatis, r on jääk.

Naturaalarvude jagatise saab kirjutada murruna.

Murru lugeja on dividend ja nimetaja jagaja.

Kuna murdosa lugeja on dividend ja nimetaja jagaja, usun, et murru rida tähendab jagamist. Mõnikord on mugav kirjutada jagamine murruna ilma märki ":" kasutamata.

Naturaalarvude m ja n jagamise jagatise saab kirjutada murruna \(\frac(m)(n) \), kus lugeja m on dividend ja nimetaja n on jagaja:
\(m:n = \frac(m)(n) \)

Järgmised reeglid vastavad tõele:

Murru \(\frac(m)(n)\ saamiseks peate jagama ühe n-ga võrdsetes osades(aktsiad) ja võta m selliseid osi.

Murru \(\frac(m)(n)\ saamiseks peate jagama arvu m arvuga n.

Terviku osa leidmiseks tuleb tervikule vastav arv jagada nimetajaga ja tulemus korrutada seda osa väljendava murdosa lugejaga.

Selle osast terviku leidmiseks peate jagama sellele osale vastava arvu lugejaga ja korrutama tulemuse selle osa väljendava murdosa nimetajaga.

Kui nii murdosa lugeja kui ka nimetaja korrutatakse sama arvuga (välja arvatud null), siis murru väärtus ei muutu:
\(\large \frac(a)(b) = \frac(a \cdot n)(b \cdot n) \)

Kui nii murdosa lugeja kui ka nimetaja jagatakse sama arvuga (välja arvatud null), siis murru väärtus ei muutu:
\(\large \frac(a)(b) = \frac(a: m)(b: m) \)
Seda omadust nimetatakse murdosa peamine omadus.

Nimetatakse kahte viimast teisendust murdosa vähendamine.

Kui murde on vaja esitada sama nimetajaga murdudena, kutsutakse seda tegevust murdude taandamine ühise nimetajani.

Õiged ja valemurrud. Seganumbrid

Te juba teate, et murdosa saab saada, jagades terviku võrdseteks osadeks ja võttes mitu sellist osa. Näiteks murd \(\frac(3)(4)\) tähendab kolmveerandit ühest. Paljudes eelmises lõigus toodud ülesannetes kasutati murde terviku osade esitamiseks. Terve mõistus soovitab, et osa peaks alati olema väiksem kui tervik, aga kuidas on siis lood selliste murdudega, nagu näiteks \(\frac(5)(5)\) või \(\frac(8)(5)\)? On selge, et see ei kuulu enam üksusesse. Tõenäoliselt seepärast kutsutaksegi murde, mille lugeja on nimetajast suurem või sellega võrdne ebaõiged murded. Ülejäänud murde, st murde, mille lugeja on nimetajast väiksem, nimetatakse õiged murded.

Nagu teate, võib mis tahes harilikku murru, nii õiget kui ka valet, pidada lugeja jagamise tulemuseks nimetajaga. Seetõttu ei tähenda termin matemaatikas erinevalt tavakeelest seda, et me tegime midagi valesti, vaid ainult seda, et selle murru lugeja on nimetajast suurem või sellega võrdne.

Kui arv koosneb täisarvust osast ja murdosast, siis selline fraktsioone nimetatakse segatud.

Näiteks:
\(5:3 = 1\frac(2)(3)\) : 1 - terve osa, ja \(\frac(2)(3)\) on murdosa.

Kui murdosa \(\frac(a)(b)\) lugeja jagub arvuga naturaalarv n, siis selle murdosa jagamiseks n-ga peate jagama selle lugeja selle arvuga:
\(\large \frac(a)(b) : n = \frac(a:n)(b) \)

Kui murdosa \(\frac(a)(b)\) lugeja ei jagu naturaalarvuga n, siis selle murdosa jagamiseks n-ga peate selle nimetaja selle arvuga korrutama:
\(\large \frac(a)(b) : n = \frac(a)(bn) \)

Pange tähele, et teine ​​reegel kehtib ka siis, kui lugeja jagub n-ga. Seetõttu saame seda kasutada siis, kui esmapilgul on raske kindlaks teha, kas murru lugeja jagub n-ga või mitte.

Tegevused murdarvudega. Murdude lisamine.

Murdarvudega saab sooritada aritmeetilisi tehteid nagu naturaalarvudega. Vaatame kõigepealt murdude lisamist. Sarnaste nimetajatega murde on lihtne lisada. Leiame näiteks \(\frac(2)(7)\) ja \(\frac(3)(7)\) summa. On lihtne mõista, et \(\frac(2)(7) + \frac(2)(7) = \frac(5)(7) \)

Samade nimetajatega murdude liitmiseks peate lisama nende lugejad ja jätma nimetaja samaks.

Tähtede abil saab sarnaste nimetajatega murdude lisamise reegli kirjutada järgmiselt:
\(\large \frac(a)(c) + \frac(b)(c) = \frac(a+b)(c) \)

Kui teil on vaja lisada murde koos erinevad nimetajad, siis tuleb need kõigepealt ühisele nimetajale viia. Näiteks:
\(\large \frac(2)(3)+\frac(4)(5) = \frac(2\cdot 5)(3\cdot 5)+\frac(4\cdot 3)(5\cdot 3) ) = \frac(10)(15)+\frac(12)(15) = \frac(10+12)(15) = \frac(22)(15) \)

Murdude, nagu ka naturaalarvude puhul kehtivad liitmise kommutatiivsed ja assotsiatiivsed omadused.

Segafraktsioonide lisamine

Nimetatakse selliseid tähistusi nagu \(2\frac(2)(3)\). segafraktsioonid. Sel juhul kutsutakse numbrit 2 terve osa segamurd ja arv \(\frac(2)(3)\) on selle murdosa. Kirje \(2\frac(2)(3)\) loetakse järgmiselt: "kaks ja kaks kolmandikku."

Jagades arvu 8 arvuga 3, saate kaks vastust: \(\frac(8)(3)\) ja \(2\frac(2)(3)\). Need väljendavad sama murdarvu, st \(\frac(8)(3) = 2 \frac(2)(3)\)

Seega esitatakse vale murd \(\frac(8)(3)\) segamurruna \(2\frac(2)(3)\). Sellistel juhtudel öeldakse, et valest murdosast tõstis esile kogu osa.

Murdude lahutamine (murdarvud)

Lahutamine murdarvud, nagu naturaalarvudki, määratakse liitmise tegevuse alusel: ühest arvust teise lahutamine tähendab arvu leidmist, mis teisele liitmisel annab esimese. Näiteks:
\(\frac(8)(9)-\frac(1)(9) = \frac(7)(9) \) alates \(\frac(7)(9)+\frac(1)(9) = \frac(8)(9)\)

Sarnaste nimetajatega murdude lahutamise reegel on sarnane selliste murdude liitmise reegliga:
Samade nimetajatega murdude erinevuse leidmiseks peate lahutama teise murdosa lugeja esimese murru lugejast ja jätma nimetaja samaks.

Tähtede abil kirjutatakse see reegel järgmiselt:
\(\large \frac(a)(c)-\frac(b)(c) = \frac(a-b)(c) \)

Murdude korrutamine

Murru korrutamiseks murdosaga peate korrutama nende lugejad ja nimetajad ning kirjutama esimese korrutise lugejaks ja teise nimetajaks.

Tähtede abil saab murdude korrutamise reegli kirjutada järgmiselt:
\(\large \frac(a)(b) \cdot \frac(c)(d) = \frac(a \cdot c)(b \cdot d) \)

Sõnastatud reegli abil saate murdosa korrutada naturaalarvuga, segamurruga ja ka segamurrud. Selleks peate kirjutama naturaalarvu murdena, mille nimetaja on 1, segamurru - vale murruna.

Korrutamise tulemust tuleks (võimaluse korral) lihtsustada, vähendades murdosa ja eraldades kogu vale murdosa.

Murdude, nagu ka naturaalarvude puhul kehtivad korrutamise kommutatiivsed ja kombinatiivsed omadused, samuti korrutamise jaotusomadused liitmise suhtes.

Murdude jagamine

Võtame murdosa \(\frac(2)(3)\) ja pöörame selle ümber, vahetades lugeja ja nimetaja. Saame murdosa \(\frac(3)(2)\). Seda murdosa nimetatakse tagurpidi murrud \(\frac(2)(3)\).

Kui nüüd murru \(\frac(3)(2)\ "tagurdada", saame algse murru \(\frac(2)(3)\). Seetõttu nimetatakse selliseid murde nagu \(\frac(2)(3)\) ja \(\frac(3)(2)\). vastastikku pöördvõrdeline.

Näiteks murrud \(\frac(6)(5) \) ja \(\frac(5)(6) \), \(\frac(7)(18) \) ja \(\frac (18) )(7)\).

Tähtede abil saab pöördmurrud kirjutada järgmiselt: \(\frac(a)(b) \) ja \(\frac(b)(a) \)

On selge, et pöördmurdude korrutis on 1. Näiteks: \(\frac(2)(3) \cdot \frac(3)(2) =1 \)

Vastastikuseid murde kasutades saate murdude jagamise taandada korrutamiseks.

Murru murruga jagamise reegel on järgmine:
Ühe murdosa teisega jagamiseks peate dividendi korrutama jagaja pöördarvuga.

Tähtede abil saab murdude jagamise reegli kirjutada järgmiselt:
\(\large \frac(a)(b) : \frac(c)(d) = \frac(a)(b) \cdot \frac(d)(c) \)

Kui dividend või jagaja on naturaalarv või segamurd, siis selleks, et kasutada murdude jagamise reeglit, tuleb see esmalt esitada valemurruna.

Murdude abil saab terve objekti sama osa kirjutada erineval viisil.

Pool ringist on pildil varjutatud

Seega on kõik need murrud võrdsed.

Mugavuse huvides kirjutatakse lisategur murru kohal paremal asuvale kaldkriipsule.

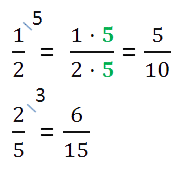
Läheme uuesti tagasi oma murdude juurde ja kirjutame need teises järjekorras.

Antud ühega võrdse murdosa saab, kui murdosa lugeja ja nimetaja jagatakse samaaegselt sama arvuga, mis ei ole võrdne nulliga.

Seda murdosa teisendamist nimetatakse murdosa vähendamine.

Murru vähendamine kirjutatakse tavaliselt järgmiselt.

Lugeja ja nimetaja kriipsutatakse läbi ning nende kõrvale kirjutatakse sama numbriga lugeja ja nimetaja jagamise tulemused (jagatised).

Pidage meeles arvu, millega lugeja ja nimetaja jagunevad.

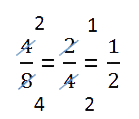
Meie näites vähendasime (st jagasime nii lugeja kui ka nimetaja) murdosa kahega, mida pidasime meeles.

Fraktsiooni vähendamist saab teha järjestikku.

Murru põhiomadus

Sõnastame murdu põhiomaduse.

Kui murdosa lugeja ja nimetaja korrutada või jagada sama arvuga, mis ei ole võrdne nulliga, saad murru, mis on võrdne antud ühega.

Kirjutame selle omaduse sõnasõnaliste väljenditena.

, kus "a", "b" ja "k" on naturaalarvud.

Murdude taandamine, reeglid ja näited murdude vähendamisest.

Selles artiklis vaatleme üksikasjalikult, kuidas redutseerivad fraktsioonid. Esiteks arutleme selle üle, mida nimetatakse murdosa vähendamiseks. Pärast seda räägime taandatava murdosa taandamisest taandamatuks vormiks. Järgmisena saame murdarvude vähendamise reegli ja lõpuks vaatleme näiteid selle reegli rakendamisest.

Leheküljel navigeerimine.

Mida tähendab murdosa vähendamine?

Teame, et harilikud murded jagunevad taandatavateks ja taandamatuteks murdudeks. Nimedest võib aimata, et taandatavaid murde saab taandada, taandamatuid aga mitte.

Mida tähendab murdosa vähendamine? Vähendage fraktsiooni- see tähendab, et lugeja ja nimetaja jagatakse nende positiivsega ja erineb ühtsusest ühine jagaja. Selge on see, et murru redutseerimise tulemusena saadakse uus väiksema lugeja ja nimetajaga murd ning murru põhiomaduse tõttu on saadud murd võrdne esialgsega.

Näiteks vähendame harilikku murru 8/24, jagades selle lugeja ja nimetaja 2-ga. Teisisõnu, vähendame murdosa 8/24 2 võrra. Kuna 8:2=4 ja 24:2=12, on selle vähendamise tulemuseks murdosa 4/12, mis on võrdne algse murdarvuga 8/24 (vt võrdsed ja ebavõrdsed murrud). Selle tulemusena on meil .

Tavaliste murdude redutseerimine taandamatule kujule

Tavaliselt on murdosa vähendamise lõppeesmärk saada taandamatu murd, mis on võrdne algse taandatava fraktsiooniga. Selle eesmärgi saab saavutada, vähendades algset taandatavat murdosa selle lugeja ja nimetaja suurima ühisjagaja võrra. Sellise redutseerimise tulemusena saadakse alati taandamatu murd. Tõepoolest, murdosa on taandamatu, kuna GCD omaduste põhjal on teada, et Ja - vastastikku algarvud. Siinkohal ütleme, et murru lugeja ja nimetaja suurim ühisjagaja on suurim arv, mille võrra seda murdu saab vähendada.

Niisiis, hariliku murdosa redutseerimine taandamatuks vormiks seisneb algse taandatava murru lugeja ja nimetaja jagamises nende gcd-ga.

Vaatame näidet, mille puhul pöördume tagasi murdarvu 8/24 juurde ja vähendame seda arvude 8 ja 24 suurima ühisjagaja võrra, mis on võrdne 8-ga. Kuna 8:8=1 ja 24:8=3, jõuame taandamatu murduni 1/3. Niisiis, .

Pange tähele, et fraas "vähendada murdosa" tähendab sageli algse fraktsiooni vähendamist selle taandamatule kujule. Teisisõnu tähendab murdosa vähendamine sageli lugeja ja nimetaja jagamist nende suurima ühisteguriga (mitte mis tahes ühisteguriga).

Kuidas murdosa vähendada? Murdude vähendamise reeglid ja näited

Jääb üle vaadata vaid murdude vähendamise reeglit, mis selgitab, kuidas antud murdosa vähendada.

Murdude vähendamise reegel koosneb kahest etapist:

• esiteks leitakse murru lugeja ja nimetaja gcd;
• teiseks, murru lugeja ja nimetaja jagatakse nende gcd-ga, mis annab algse taandamatu murdu.

Teeme asja korda näide murdosa vähendamisest vastavalt märgitud reeglile.

www.cleverstudents.ru

Murdude vähendamine. Mida tähendab murdosa vähendamine?

Murdude taandamine on vajalik selleks, et murda näiteks avaldise lahendamise tulemusena saadud vastuses lihtsamale kujule taandada.

Murdude taandamine, määratlus ja valem.

Mis on murdude vähendamine? Mida tähendab murdosa vähendamine?

Definitsioon:
Murdude vähendamine- see on murdosa lugeja ja nimetaja jagamine sama positiivse arvuga, mis ei ole võrdne nulli ja ühega. Taandamise tulemusena saadakse väiksema lugeja ja nimetajaga murd, mis on põhiomaduse järgi võrdne eelmise murruga ratsionaalsed arvud.

Valem fraktsioonide vähendamiseks ratsionaalarvude põhiomadused.

Vaatame näidet:
Vähenda murdosa \(\frac \)

Lahendus:
Saame lisada murdosa algteguriteks ja tühistada tavalised tegurid.

Vastus: pärast redutseerimist saime murdosa \(\frac\). Ratsionaalarvude põhiomaduse järgi on alg- ja tulemmurrud võrdsed.

Kuidas murdosasid vähendada? Murru redutseerimine selle taandamatule kujule.

Selle tulemusel taandamatu murdosa saamiseks vajame leida suurim ühisjagaja (GCD) murru lugeja ja nimetaja jaoks.

GCD leidmiseks on mitu võimalust; näites kasutame arvude jaotamist algteguriteks.

Hankige taandamatu murd \(\frac\).

Lahendus:
Leiame GCD(48, 136). Kirjutame arvud 48 ja 136 algteguriteks.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
GCD(48; 136)= 2⋅2⋅2=6

Reegel murdosa redutseerimiseks taandamatuks vormiks.

1. Peate leidma lugeja ja nimetaja suurima ühise jagaja.
2. Jagamise tulemusel taandamatu murdu saamiseks peate lugeja ja nimetaja jagama suurima ühise jagajaga.

Näide:
Vähendage murdosa \(\frac\).

Lahendus:
Leiame GCD(152, 168). Kirjutame arvud 152 ja 168 algteguriteks.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
GCD(152; 168)= 2⋅2⋅2=6

Vastus: \(\frac \) on taandamatu murd.

Sobimatute murdude vähendamine.

Kuidas lühendada õige murdosa?
Murdude vähendamise reeglid on õigete ja valede murdude puhul samad.

Vaatame näidet:
Vähendage vale murdosa \(\frac\).

Lahendus:
Kirjutame lugeja ja nimetaja lihtsateks teguriteks. Ja siis vähendame ühiseid tegureid.

Segafraktsioonide vähendamine.

Segamurrud järgivad samu reegleid kui tavalised murrud. Ainus erinevus on see, et me saame ärge puudutage tervet osa, vaid vähendage murdosa või Teisendage segamurd valeks murdarvuks, vähendage seda ja teisendage see tagasi õigeks murdarvuks.

Vaatame näidet:
Tühistage segamurd \(2\frac\).

Lahendus:
Lahendame selle kahel viisil:
Esimene viis:
Kirjutame murdosa lihtsateks teguriteks, kuid me ei puuduta kogu osa.

Teine viis:
Teisendame selle esmalt valeks murdeks ja kirjutame seejärel algteguriteks ja vähendame. Teisendame saadud valemurru õigeks murruks.

Seotud küsimused:
Kas saate liitmisel või lahutamisel murde vähendada?
Vastus: ei, kõigepealt tuleb vastavalt reeglitele lisada või lahutada murde ja alles siis neid vähendada. Vaatame näidet:

Lahendus:
Sageli teevad nad vea, vähendades lugejas ja nimetajas samu numbreid, meie puhul arvu 20, kuid neid ei saa vähendada enne, kui olete liitmise ja lahutamise lõpetanud.

Milliste arvude võrra saate murdosa vähendada?
Vastus: Murru saab vähendada suurima ühisteguri või lugeja ja nimetaja ühisjagaja võrra. Näiteks murd \(\frac \).

Kirjutame arvud 100 ja 150 algteguriteks.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Suurim ühine jagaja on arv gcd(100, 150)= 2⋅5⋅5=50

Saime taandamatu murru \(\frac \).

Kuid alati pole vaja jagada gcd-ga; taandamatut murdu pole alati vaja; murdu saab vähendada lugeja ja nimetaja lihtsa jagajaga. Näiteks arvudel 100 ja 150 on ühine jagaja 2. Vähendame murdosa \(\frac \) 2 võrra.

Saime taandatava murdosa \(\frac\).

Milliseid fraktsioone saab vähendada?
Vastus: Saate vähendada murde, milles lugejal ja nimetajal on ühine jagaja. Näiteks murd \(\frac \). Arvudel 4 ja 8 on arv, millega nad mõlemad jaguvad – arv 2. Seetõttu saab sellist murdosa arvu 2 võrra vähendada.

Näide:
Võrrelge kahte murdosa \(\frac \) ja \(\frac \).

Need kaks murdosa on võrdsed. Vaatame murdu \(\frac \) lähemalt:

Kaks murdu on võrdsed siis ja ainult siis, kui üks neist saadakse, taandades teise murdosa lugeja ja nimetaja ühise teguri võrra.

Näide:
Võimalusel vähendage järgmisi murde: a) \(\frac \) b) \(\frac \) c) \(\frac \) d) \(\frac \)

Tehted harilike murrudega

Fraktsiooni laiendamine. Murdosa vähendamine. Murdude võrdlemine.

Taandamine ühisele nimetajale. Liitmine ja lahutamine fraktsioonid

Murdude korrutamine. Murdude jagamine .

Fraktsiooni laiendamine. Murru väärtus ei muutu, kui korrutate selle lugeja ja nimetaja sama arvuga, mis ei ole null. murdosa laienemine. Näiteks,



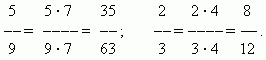
Murdosa vähendamine. Murru väärtus ei muutu, kui jagate selle lugeja ja nimetaja sama arvuga, mis ei ole null.. Seda teisendust nimetatakse murdosa vähendamine. Näiteks,



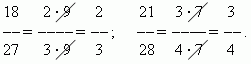
Murdude võrdlemine. Kahest samade lugejatega murdest on suurem see, mille nimetaja on väiksem:



Kahest sama nimetajaga murdest on suurem see, mille lugeja on suurem:



Erinevate lugejate ja nimetajatega murdude võrdlemiseks peate neid laiendama, et viia need ühise nimetajani.

NÄIDE Võrrelge kahte murdosa:

Laiendame esimest murdu teise ja teist esimese nimetaja võrra:

Siin kasutatud teisendust nimetatakse murdude taandamine ühise nimetajani.

Murdude liitmine ja lahutamine. Kui murdude nimetajad on samad, siis tuleb murdude liitmiseks liita nende lugejad ja murdude lahutamiseks nende lugejad (samas järjekorras). Saadud summa või erinevus on tulemuse lugeja; nimetaja jääb samaks. Kui murdude nimetajad on erinevad, tuleb esmalt murded taandada ühisele nimetajale. Segaarvude liitmisel liidetakse nende tervik- ja murdosa eraldi. Segaarvude lahutamisel soovitame need esmalt teisendada ebaõigeteks murdudeks, seejärel lahutada üks teisest ja seejärel teisendada tulemus vajadusel uuesti segaarvukujule.



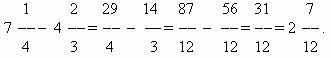
Murdude korrutamine. Arvu korrutamine murdosaga tähendab selle korrutamist lugejaga ja korrutise jagamist nimetajaga. Seetõttu on meil üldreegel murdude korrutamine: murdude korrutamiseks peate korrutama nende lugejad ja nimetajad eraldi ning jagama esimese korrutise teisega.

NÄIDE

Murrude jagamine. Arvu jagamiseks murdosaga peate selle arvu korrutama pöördmurruga. See reegel tuleneb jagamise definitsioonist (vt jaotist "Aritmeetilised tehted").

NÄIDE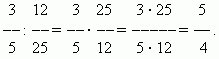

Murdude korrutamine ja jagamine

Eelmisel korral õppisime murdude liitmist ja lahutamist (vt õppetükki “Murdude liitmine ja lahutamine”). Nende toimingute kõige keerulisem osa oli murdude ühise nimetajani viimine.

Nüüd on aeg tegeleda korrutamise ja jagamisega. Head uudised on see, et need toimingud on isegi lihtsamad kui liitmine ja lahutamine. Esmalt vaatleme lihtsaimat juhtumit, kui on kaks positiivset murdu ilma eraldatud täisarvuta.

Kahe murru korrutamiseks peate nende lugejad ja nimetajad eraldi korrutama. Esimene number on uue murru lugeja ja teine ​​on nimetaja.

Kahe murru jagamiseks peate korrutama esimese murdosa "ümberpööratud" teise murruga.

Definitsioonist järeldub, et murdude jagamine taandub korrutamiseks. Murru ümberpööramiseks vahetage lihtsalt lugeja ja nimetaja. Seetõttu käsitleme kogu õppetunni jooksul peamiselt korrutamist.

Korrutamise tulemusena võib tekkida (ja sageli tekib) taandatav murd – seda tuleb loomulikult vähendada. Kui pärast kõiki vähendamisi osutub murdosa valeks, tuleks kogu osa esile tõsta. Mida aga korrutamisega kindlasti ei juhtu, on taandamine ühisele nimetajale: ei mingeid ristimeetodeid, suurimaid tegureid ja väikseimaid ühiseid kordusi.



Murdude korrutamine täisosadega ja negatiivsete murdudega

Kui murrud sisaldavad täisarvu, tuleb need teisendada sobimatuteks osadeks ja alles seejärel korrutada vastavalt ülaltoodud skeemidele.

Kui murdosa lugejas, nimetajas või selle ees on miinus, saab selle korrutisest välja võtta või üldse eemaldada vastavalt järgmistele reeglitele:

1. Pluss miinusega annab miinuse;
2. Kaks negatiivset teevad jaatava.

Seni on neid reegleid kohanud vaid negatiivsete murdude liitmisel ja lahutamisel, kui oli vaja tervest osast lahti saada. Teose puhul saab neid üldistada, et "põletada" mitu puudust korraga:

3. Negatiivid kriipsutame paarikaupa maha, kuni need täielikult kaovad. Äärmuslikel juhtudel võib ellu jääda üks miinus - see, mille jaoks polnud kaaslast;
4. Kui miinuseid ei jää, on toiming lõpetatud - võite hakata korrutama. Kui viimast miinust ei kriipsutata maha, sest selle jaoks polnud paari, võtame selle korrutamise piiridest välja. Tulemuseks on negatiivne murd.

Ülesanne. Leidke väljendi tähendus:

Teisendame kõik murrud valedeks ja seejärel võtame korrutamisest välja miinused. Korrutame järelejäänud tavapäraste reeglite järgi. Saame:



Tuletan teile veel kord meelde, et esiletõstetud täisosaga murru ette ilmuv miinus viitab konkreetselt kogu murrule, mitte ainult selle tervele osale (see kehtib kahe viimase näite kohta).

Pange tähele ka negatiivsed arvud: Korrutamisel on need sulgudes. Seda tehakse selleks, et eraldada miinused korrutusmärkidest ja muuta kogu tähistus täpsemaks.

Murdude vähendamine lennult

Korrutamine on väga töömahukas toiming. Siin olevad numbrid osutuvad üsna suurteks ja probleemi lihtsustamiseks võite proovida murdosa veelgi vähendada enne korrutamist. Tõepoolest, sisuliselt on murdude lugejad ja nimetajad tavalised tegurid ja seetõttu saab neid taandada, kasutades murdosa põhiomadust. Heitke pilk näidetele:



Definitsiooni järgi on meil:



Kõikides näidetes on punasega märgitud numbrid, mida on vähendatud ja mis neist järele jääb.

Pange tähele: esimesel juhul vähendati kordajaid täielikult. Nende asemele jäävad üksused, mida üldiselt ei pea kirjutama. Teise näite puhul ei olnud võimalik saavutada täielikku vähendamist, kuid arvutuste kogusumma siiski vähenes.

Kuid ärge kunagi kasutage seda tehnikat murdude liitmisel ja lahutamisel! Jah, mõnikord on sarnaseid numbreid, mida soovite lihtsalt vähendada. Vaata siit:

Sa ei saa seda teha!

Viga tekib seetõttu, et liitmisel annab murdosa lugeja summa, mitte arvude korrutise. Järelikult on võimatu rakendada murru põhiomadust, kuna see omadus käsitleb konkreetselt arvude korrutamist.

Murdude vähendamiseks pole lihtsalt muid põhjuseid, seega näeb eelmise probleemi õige lahendus välja järgmine:

Nagu näha, osutus õige vastus mitte nii ilus. Üldiselt olge ettevaatlik.

See artikkel jätkab algebraliste murdude teisendamise teemat: kaaluge sellist toimingut kui algebraliste murdude vähendamist. Defineerime mõiste ise, sõnastame redutseerimisreegli ja analüüsime praktilisi näiteid.

Yandex.RTB R-A-339285-1

Algebralise murru taandamise tähendus

Harilikke murde käsitlevates materjalides vaatlesime selle vähendamist. Me määratlesime murdosa vähendamise kui selle lugeja ja nimetaja jagamise ühise teguriga.

Algebralise murru vähendamine on sarnane tehe.

Definitsioon 1

Algebralise murru taandamine on selle lugeja ja nimetaja jagamine ühise teguriga. Sel juhul, erinevalt hariliku murru vähendamisest (ühisnimetaja saab olla ainult arv), võib algebralise murru lugeja ja nimetaja ühiseks teguriks olla polünoom, eriti monoom või arv.

Näiteks algebralist murdosa 3 x 2 + 6 x y 6 x 3 y + 12 x 2 y 2 saab taandada arvuga 3, mille tulemuseks on: x 2 + 2 x y 6 x 3 · y + 12 · x 2 · y 2 . Sama murdosa saame taandada muutuja x võrra ja see annab meile avaldise 3 x + 6 y 6 x 2 y + 12 x y 2. Samuti on võimalik etteantud murdosa vähendada monoomi võrra 3 x või mõni polünoomidest x + 2 a, 3 x + 6 a , x 2 + 2 x y või 3 x 2 + 6 x a.

Algebralise murru vähendamise lõppeesmärk on lihtsama vormi murd, parimal juhul taandamatu murd.

Kas kõik algebralised murrud kuuluvad taandamisele?

Jällegi, tavaliste fraktsioonide materjalide põhjal teame, et on olemas taandatavad ja taandumatud murded. Taandumatud murrud on murrud, millel pole muid ühiseid lugeja ja nimetaja tegureid peale 1.

Sama on algebraliste murdudega: neil võivad lugejas ja nimetajas olla ühised tegurid või mitte. Ühiste tegurite olemasolu võimaldab algset murdosa redutseerimise kaudu lihtsustada. Kui ühiseid tegureid pole, ei ole võimalik antud murdosa redutseerimismeetodi abil optimeerida.

Üldjuhul on murdosa tüüpi arvestades üsna raske aru saada, kas seda saab vähendada. Muidugi on mõnel juhul ilmne ühise teguri olemasolu lugeja ja nimetaja vahel. Näiteks algebralises murrus 3 x 2 3 y on üsna selge, et ühine tegur on arv 3.

Murrus - x · y 5 · x · y · z 3 saame ka kohe aru, et seda saab vähendada x, y või x · y võrra. Ja veel, palju sagedamini on näiteid algebralistest murdudest, kui lugeja ja nimetaja ühistegurit pole nii lihtne näha ja veelgi sagedamini see lihtsalt puudub.

Näiteks saame murdosa x 3 - 1 x 2 - 1 vähendada x - 1 võrra, samas kui määratud ühistegurit kirjes pole. Kuid murdosa x 3 - x 2 + x - 1 x 3 + x 2 + 4 · x + 4 ei saa vähendada, kuna lugejal ja nimetajal pole ühist tegurit.

Seega ei ole algebralise murru taandatavuse määramise küsimus nii lihtne ja sageli on lihtsam töötada antud kuju murdosaga, kui proovida välja selgitada, kas see on taandatav. Sel juhul toimuvad sellised teisendused, mis võimaldavad konkreetsetel juhtudel määrata lugeja ja nimetaja ühisteguri või teha järelduse murdosa taandatamatuse kohta. Vaatleme seda küsimust üksikasjalikult artikli järgmises lõigus.

Algebraliste murdude vähendamise reegel

Algebraliste murdude vähendamise reegel koosneb kahest järjestikusest toimingust:

• lugeja ja nimetaja ühistegurite leidmine;
• kui neid leitakse, viiakse fraktsiooni vähendamine läbi otse.

Kõige mugavam meetod ühisnimetajate leidmiseks on arvutada antud algebralise murru lugejas ja nimetajas esinevad polünoomid. See võimaldab teil kohe selgelt näha ühiste tegurite olemasolu või puudumist.

Algebralise murru redutseerimise tegevus põhineb algebralise murru põhiomadusel, mida väljendatakse võrdsusega määramata, kus a, b, c on mõned polünoomid ning b ja c on nullist erinevad. Esimene samm on murdosa taandamine kujule a · c b · c, milles märkame kohe ühistegurit c. Teine samm on reduktsiooni teostamine, s.o. üleminek murdosale vormist a b .

Tüüpilised näited

Vaatamata mõningasele ilmselgele selgitame erijuhtum kui algebralise murru lugeja ja nimetaja on võrdsed. Sarnased murrud on identselt võrdsed 1-ga selle murdosa muutujate kogu ODZ-s:

5 5 = 1; - 2 3 - 2 3 = 1; x x = 1; - 3, 2 x 3 - 3, 2 x 3 = 1; 1 2 · x - x 2 · y 1 2 · x - x 2 · y ;

Kuna tavalised murrud on algebraliste murdude erijuht, tuletagem meelde, kuidas neid redutseeritakse. Lugejasse ja nimetajasse kirjutatud naturaalarvud arvestatakse algteguriteks, seejärel ühistegurid tühistatakse (kui neid on).

Näiteks 24 1260 = 2 2 2 3 2 2 3 3 5 7 = 2 3 5 7 = 2 105

Lihtsate identsete tegurite korrutist saab kirjutada astmetena ja murdosa vähendamise protsessis kasutada identsete alustega astmete jagamise omadust. Siis oleks ülaltoodud lahendus järgmine:

24 1260 = 2 3 3 2 2 3 2 5 7 = 2 3 - 2 3 2 - 1 5 7 = 2 105

(lugeja ja nimetaja jagatud ühise teguriga 2 2 3). Või selguse huvides anname korrutamise ja jagamise omaduste põhjal lahendusele järgmise kuju:

24 1260 = 2 3 3 2 2 3 2 5 7 = 2 3 2 2 3 3 2 1 5 7 = 2 1 1 3 1 35 = 2 105

Analoogiliselt viiakse läbi algebraliste murdude redutseerimine, milles lugejal ja nimetajal on täisarvu koefitsientidega monomial.

Näide 1

Algebraline murd on antud - 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z. Seda tuleb vähendada.

Lahendus

Antud murru lugeja ja nimetaja on võimalik kirjutada lihtsate tegurite ja muutujate korrutisena ning seejärel redutseerida:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = - 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · c · z = = - 3 · 3 · a · a · a 2 · c · c · c · c · c · c = - 9 a 3 2 c 6

Ratsionaalsem viis oleks aga kirjutada lahendus volitustega avaldisena:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = - 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = - 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = - 3 3 - 1 2 · a 5 - 2 1 · 1 · 1 c 7 - 1 · 1 = · - 3 2 · a 3 2 · c 6 = · - 9 · a 3 2 · c 6 .

Vastus:- 27 a 5 b 2 c z 6 a 2 b 2 c 7 z = - 9 a 3 2 c 6

Kui algebralise murru lugeja ja nimetaja sisaldavad murdarvulisi koefitsiente, on edasiseks tegevuseks kaks võimalikku võimalust: kas jagada need murdosa koefitsiendid eraldi või kõigepealt vabaneda murdosakordajad, korrutades lugeja ja nimetaja mõne naturaalarvuga. Viimane teisendus viiakse läbi algebralise murru põhiomaduse tõttu (selle kohta saate lugeda artiklist "Algebralise murru taandamine uuele nimetajale").

Näide 2

Antud murd on 2 5 x 0, 3 x 3. Seda tuleb vähendada.

Lahendus

Murru on võimalik vähendada järgmiselt:

2 5 x 0, 3 x 3 = 2 5 3 10 x x 3 = 4 3 1 x 2 = 4 3 x 2

Proovime probleemi lahendada teisiti, olles esmalt vabanenud murdosakordajatest - korrutage lugeja ja nimetaja nende koefitsientide nimetajate vähima ühiskordsega, s.o. LCM-is (5, 10) = 10. Siis saame:

2 5 x 0, 3 x 3 = 10 2 5 x 10 0, 3 x 3 = 4 x 3 x 3 = 4 3 x 2.

Vastus: 2 5 x 0, 3 x 3 = 4 3 x 2

Kui me vähendame algebralisi murde üldine vaade, milles lugejad ja nimetajad võivad olla kas mono- või polünoomid, võib tekkida probleem, kui ühistegur pole alati kohe nähtav. Või pealegi pole seda lihtsalt olemas. Seejärel arvutatakse ühisteguri määramiseks või selle puudumise fakti registreerimiseks algebralise murru lugeja ja nimetaja.

Näide 3

Ratsionaalne murd 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 - 49 · b 3 on antud. Seda tuleb vähendada.

Lahendus

Arvestame polünoomid lugejas ja nimetajas. Paneme selle sulgudest välja:

2 a 2 b 2 + 28 a b 2 + 98 b 2 a 2 b 3 - 49 b 3 = 2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49)

Näeme, et sulgudes olevat avaldist saab teisendada lühendatud korrutusvalemite abil:

2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49) = 2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7)

On selgelt näha, et murdosa on võimalik ühise teguri võrra vähendada b 2 (a + 7). Teeme vähendamise:

2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7) = 2 (a + 7) b (a - 7) = 2 a + 14 a b - 7 b

Kirjutame lühilahenduse ilma selgituseta võrduste ahelana:

2 a 2 b 2 + 28 a b 2 + 98 b 2 a 2 b 3 - 49 b 3 = 2 b 2 (a 2 + 14 a + 49) b 3 (a 2 - 49) = = 2 b 2 (a + 7) 2 b 3 (a - 7) (a + 7) = 2 (a + 7) b (a - 7) = 2 a + 14 a b - 7 b

Vastus: 2 a 2 b 2 + 28 a b 2 + 98 b 2 a 2 b 3 - 49 b 3 = 2 a + 14 a b - 7 b.

Juhtub, et ühiseid tegureid varjavad arvulised koefitsiendid. Seejärel on murdude vähendamisel optimaalne panna lugeja ja nimetaja suuremate astmetega arvulised tegurid sulgudest välja.

Näide 4

Antud algebraline murd 1 5 · x - 2 7 · x 3 · y 5 · x 2 · y - 3 1 2 . Võimaluse korral on vaja seda vähendada.

Lahendus

Esmapilgul ei ole lugejal ja nimetajal ühist nimetajat. Proovime aga antud murdosa teisendada. Võtame lugejast välja teguri x:

1 5 x - 2 7 x 3 a 5 x 2 a - 3 1 2 = x 1 5 - 2 7 x 2 a 5 x 2 a - 3 1 2

Nüüd näete mõningast sarnasust sulgudes oleva avaldise ja nimetaja avaldise vahel, mis tuleneb x 2 y . Võtame välja nende polünoomide suuremate astmete arvulised koefitsiendid:

x 1 5 - 2 7 x 2 y 5 x 2 y - 3 1 2 = x - 2 7 - 7 2 1 5 + x 2 y 5 x 2 y - 1 5 3 1 2 = = - 2 7 x - 7 10 + x 2 a 5 x 2 a - 7 10

Nüüd muutub ühine tegur nähtavaks, teostame vähendamise:

2 7 x - 7 10 + x 2 a 5 x 2 a - 7 10 = - 2 7 x 5 = - 2 35 x

Vastus: 1 5 x - 2 7 x 3 y 5 x 2 y - 3 1 2 = - 2 35 x .

Rõhutagem, et kokkutõmbumisoskus ratsionaalsed murded sõltub polünoomide faktorite arvutamise võimest.

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

Veebikalkulaator täidab algebraliste murdude vähendamine vastavalt murdude redutseerimise reeglile: algmurru asendamine võrdse murdarvuga, kuid väiksema lugeja ja nimetajaga, s.o. Murru lugeja ja nimetaja samaaegne jagamine nende ühise suurima ühisteguriga (GCD). Kalkulaator kuvab ka üksikasjaliku lahenduse, mis aitab teil mõista vähendamise järjestust.

Arvestades:

Lahendus:

Murdarvu vähendamise teostamine

algebralise murdarvu vähendamise teostamise võimaluse kontrollimine

1) Murru lugeja ja nimetaja suurima ühisjagaja (GCD) määramine

algebralise murru lugeja ja nimetaja suurima ühisjagaja (GCD) määramine

2) Murru lugeja ja nimetaja vähendamine

algebralise murru lugeja ja nimetaja vähendamine

3) Murru terve osa valimine

eraldades kogu algebralise murru osa

4) Algebralise murru teisendamine kümnendmurruks

algebralise murru teisendamine kümnend

Abi projekti veebisaidi arendamiseks

Hea saidi külastaja.
Kui te ei leidnud seda, mida otsisite, kirjutage sellest kindlasti kommentaaridesse, mis sellel saidil hetkel puudu on. See aitab meil mõista, millises suunas peame edasi liikuma ning peagi saavad ka teised külastajad vajaliku materjali kätte.
Kui sait osutus teile kasulikuks, annetage see sait projektile ainult 2 ₽ ja me teame, et liigume õiges suunas.

Täname, et külastasite!

I. Algebralise murru vähendamise protseduur võrgukalkulaatori abil:

1. Algebralise murru vähendamiseks sisestage vastavatele väljadele murdosa lugeja ja nimetaja väärtused. Kui murdosa on segatud, siis täida ka kogu murdosale vastav väli. Kui murd on lihtne, jätke kogu osa väli tühjaks.
2. Negatiivse murru määramiseks asetage kogu murdosale miinusmärk.
3. Sõltuvalt määratud algebralisest murdosast teostatakse automaatselt järgmine toimingute jada:

• murru lugeja ja nimetaja suurima ühisjagaja (GCD) määramine;
• murru lugeja ja nimetaja vähendamine gcd võrra;
• kogu murdosa esiletõstmine, kui lõpliku murru lugeja on nimetajast suurem.
• lõpliku algebralise murru teisendamine kümnendmurruksümardatuna lähima sajandikuni.

II. Viitamiseks:

Murd on arv, mis koosneb ühiku ühest või mitmest osast (murrust). Harilik murd(lihtmurd) kirjutatakse kahe arvuna (murru lugeja ja murru nimetaja), mis on eraldatud horisontaalse ribaga (murruriba), mis näitab jagamismärki. Murru lugeja on murrujoone kohal asuv arv. Lugeja näitab, mitu aktsiat tervikust võeti. Murru nimetaja on murrujoone all olev arv. Nimetaja näitab, mitmeks võrdseks osaks on tervik jagatud. Lihtmurd on murd, millel ei ole tervet osa. Lihtmurd võib olla õige või vale. Õige murd on murd, mille lugeja on nimetajast väiksem, seega on õige murd alati väiksem kui üks. Õigete murdude näide: 8/7, 11/19, 16/17. Vale murd on murd, mille lugeja on nimetajast suurem või sellega võrdne, seega on vale murd alati suurem kui üks või sellega võrdne. Sobimatute murdude näide: 7/6, 8/7, 13/13. segamurd on arv, mis sisaldab täisarvu ja õiget murdosa ning tähistab selle täisarvu ja õige murdosa summat. Mis tahes segafraktsiooni saab teisendada valeks fraktsiooniks lihtmurd. Segafraktsioonide näide: 1¼, 2½, 4¾.

III. Märge:

1. Lähteandmete plokk on kollasega esile tõstetud, eraldatud vahearvutusplokk sinine , lahendusplokk on roheliselt esile tõstetud.
2. Tavaliste või segamurdude liitmiseks, lahutamiseks, korrutamiseks ja jagamiseks kasutage võrgus olevat murrukalkulaatorit üksikasjalik lahendus.

Niisiis, me juba teame, et murdosa lugejat ja nimetajat saab korrutada ja jagada sama arvuga, murdosa ei muutu. Vaatleme kolme lähenemisviisi:

Lähenege ühele.

Vähendamiseks jagage lugeja ja nimetaja ühise jagajaga. Vaatame näiteid:

Lühendame:

Toodud näidetes näeme kohe, milliseid jagajaid redutseerimiseks võtta. Protsess on lihtne – läbime 2,3,4,5 ja nii edasi. Enamiku koolikursuste näidete puhul on see täiesti piisav. Aga kui see on murdosa:

Siin võib jagajate valimise protsess võtta kaua aega;). Loomulikult jäävad sellised näited kooli õppekavast välja, aga nendega tuleb hakkama saada. Allpool vaatleme, kuidas seda tehakse. Nüüd pöördume tagasi arvu vähendamise protsessi juurde.

Nagu eespool mainitud, jagasime murdosa vähendamiseks meie määratud ühisjagaja(te)ga. Kõik on õige! Lisada tuleb vaid arvude jaguvuse märgid:

- kui arv on paaris, jagub see 2-ga.

- kui arv kahest viimasest numbrist jagub 4-ga, siis arv ise jagub 4-ga.

— kui arvu moodustavate numbrite summa jagub 3-ga, siis arv ise jagub 3-ga. Näiteks 125031, 1+2+5+0+3+1=12. Kaksteist jagub 3-ga, seega 123031 jagub 3-ga.

- kui arv lõpeb 5 või 0-ga, jagub arv 5-ga.

— kui arvu moodustavate numbrite summa jagub 9-ga, siis arv ise jagub 9-ga. Näiteks 625032 =.> 6+2+5+0+3+2=18. Kaheksateist jagub 9-ga, mis tähendab, et 623032 jagub 9-ga.

Teine lähenemine.

Lühidalt öeldes taandub tegelikult kogu tegevus lugeja ja nimetaja faktoriseerimisele ning seejärel võrdsete tegurite vähendamisele lugejas ja nimetajas (see lähenemisviis on esimese lähenemisviisi tagajärg):

Visuaalselt tõmmatakse segaduse ja vigade vältimiseks võrdsed tegurid lihtsalt maha. Küsimus – kuidas arvutada arvu? Otsimise teel on vaja määrata kõik jagajad. See on omaette teema, pole keeruline, otsi infot õpikust või internetist. Koolimurdudes esinevate faktooringunumbritega ei teki suuri probleeme.

Vormiliselt saab redutseerimispõhimõtte kirjutada järgmiselt:

Kolmas lähenemine.

Siin on kõige huvitavam edasijõudnutele ja neile, kes soovivad selleks saada. Vähendame murdosa 143/273. Proovi ise! Noh, kuidas see kiiresti juhtus? Vaata nüüd!

Pöörame ümber (vahetame lugeja ja nimetaja kohti). Jagame saadud murdosa nurgaga ja teisendame selle segaarvuks, see tähendab, et valime kogu osa:

See on juba lihtsam. Näeme, et lugejat ja nimetajat saab vähendada 13 võrra:

Nüüd ärge unustage murdu uuesti tagasi pöörata, kirjutame kogu ahela üles:

Kontrollitud – see võtab vähem aega kui läbiotsimine ja jagajate kontrollimine. Tuleme tagasi meie kahe näite juurde:

Esiteks. Nurgaga jagamisel (mitte kalkulaatoril) saame:

See murdosa on muidugi lihtsam, kuid vähendamine on jällegi probleem. Nüüd analüüsime eraldi murdosa 1273/1463 ja pöörame selle ümber:

Siin on lihtsam. Võime kaaluda jagajat nagu 19. Ülejäänud ei sobi, see on selge: 190:19 = 10, 1273:19 = 67. Hurraa! Paneme kirja:

Järgmine näide. Lühendame 88179/2717.

Jagage, saame:

Eraldi analüüsime murdosa 1235/2717 ja pöörame selle ümber:

Võime kaaluda jagajat, näiteks 13 (kuni 13 ei sobi):

Lugeja 247:13=19 Nimetaja 1235:13=95

*Protsessi käigus nägime veel ühte jagajat, mis võrdub 19-ga. Selgub, et:

Nüüd kirjutame üles algse numbri:

Ja pole vahet, mis on murrus suurem - lugeja või nimetaja, kui see on nimetaja, siis pöörame selle ümber ja toimime nii, nagu kirjeldatud. Nii saame vähendada mis tahes murdosa, kolmandat lähenemist võib nimetada universaalseks.

Loomulikult ei ole ülalpool käsitletud kaks näidet lihtsad näited. Proovime seda tehnoloogiat "lihtsate" murdude peal, mida oleme juba kaalunud:

Kaks veerandit.

Seitsekümmend kaks kuuekümnendat. Lugeja on nimetajast suurem; seda pole vaja ümber pöörata:

Loomulikult rakendati sellistele kolmandat lähenemist lihtsaid näiteid lihtsalt alternatiivina. Meetod, nagu juba öeldud, on universaalne, kuid mitte mugav ja õige kõigi fraktsioonide, eriti lihtsate fraktsioonide jaoks.

Murdude mitmekesisus on suur. On oluline, et mõistaksite põhimõtteid. Ranged reeglid murdudega lihtsalt ei saa töötada. Vaatasime, mõtlesime, kuidas oleks mugavam tegutseda, ja liikusime edasi. Harjutades tulevad oskused ja te purustate neid nagu seemneid.

Järeldus:

Kui näete lugeja ja nimetaja ühist jagajat, kasutage neid vähendamiseks.

Kui teate, kuidas arvu kiiresti faktoristada, siis arvutage lugeja ja nimetaja ning seejärel vähendage.

Kui te ei suuda ühisjagajat määrata, kasutage kolmandat lähenemisviisi.

*Murdude vähendamiseks on oluline valdada taandamise põhimõtteid, mõista murdu põhiomadust, tunda lahendusviise ning olla arvutuste tegemisel äärmiselt ettevaatlik.

Ja pidage meeles! Tavaks on murdosa taandamine kuni peatumiseni, st vähendada seni, kuni on olemas ühine jagaja.

Lugupidamisega Aleksander Krutitskihh.