Laurenti seeria eraldas ainsuse punktid ja nende klassifikatsiooni. Ainus punkt
Taylori seeriad on tõhus tööriist ringis analüütiliste funktsioonide uurimiseks zol Ringpiirkonnas analüütiliste funktsioonide uurimiseks osutub võimalikuks konstrueerida laiendusi vormi positiivsetes ja negatiivsetes võimsustes (z - zq). mis üldistavad Taylori laiendusi. Seeriat (1), mida mõistetakse kahe seeria summana, nimetatakse Laurenti seeriaks. On selge, et seeria (1) konvergentsipiirkond on iga seeria (2) lähenemispiirkondade ühine osa. Otsime ta üles. Esimese seeria lähenemisala on ring, mille raadius määratakse Cauchy-Hadamardi valemiga. Konvergentsiringi sees koondub seeria (3) analüütiliseks funktsiooniks ja igas väiksema raadiusega ringis koondub see absoluutselt ja ühtlaselt. Teine rida on jõuseeria muutuja suhtes koondub seeria (5) oma lähenemisringi sees kompleksmuutuja m-*oo analüütilisele funktsioonile ja mis tahes väiksema raadiusega ringis koondub see absoluutselt ja ühtlaselt, mis tähendab, et lähenemisala seeriast (4) on ringi väliskülg – kui siis on seeriate (3) ja (4) ühine lähenemisala, on see ringikujuline rõngas, milles seeria (1) koondub analüütiliseks funktsiooniks. Veelgi enam, mis tahes ringis läheneb see absoluutselt ja ühtlaselt. Näide 1. Määrake Rad Laurent'i seeriate konvergentsipiirkond Eraldatud ainsuse punktid ja nende klassifikatsioon M Esimese seeria lähenemispiirkond on ringi väliskülg ja teise seeria konvergentsipiirkond on ringi sisekülg. see jada koondub ringideks Teoreem 15. Mis tahes funktsiooni f (z), ühetähenduslikku ja apoliitilist ringikujulises ringis, saab selles ringis esitada koonduva jada summana, mille koefitsiendid Cn on üheselt määratud ja arvutatud valemite järgi kus 7p on ring raadiusega m. Fikseerime rõnga R sees suvalise punkti z. Ehitame ringid, mille tsentrid on punktis r, mille raadiused rahuldavad võrratusi ja vaatleme uut rõngast Kasutades Cauchy integraaliteoreemi korrutisega seotud domeeni kohta, teisendame kõik summas (8) olevad integraalid eraldi. Kõigi punktide £ jaoks mööda ringjoont 7d* on täidetud ühtlaselt koonduva jada 1 1 summaarne seos. Seetõttu saab murdosa ^ esitada kujul vi- / "/ Korrutades mõlemad osad pideva funktsiooniga (O ja teostades termini haaval integreerimisel piki ringi, saame, et teostame teise integraali teisenduse mõnevõrra erinevalt. Kõikide punktide £ jaoks ringil ir> seos kehtib. Seetõttu võib murdosa ^ esitada summana ühtlaselt koonduv jada. Korrutades mõlemad pooled pideva funktsiooniga) ja integreerides termiliselt piki ringi 7/, saame, et Pange tähele, et integrandid valemites (10) ja (12) on analüütilised funktsioonid ringrõngas. Seetõttu Cauchy teoreem, vastavate integraalide väärtused ei muutu, kui asendame ringid 7/r ja 7r/ mis tahes ringiga. See võimaldab kombineerida valemeid (10) ja (12) , Asendades integraalid paremal pool valem (8) vastavalt nende avaldistega (9) ja (11) saame vajaliku laienduse Kuna z on rõnga suvaline punkt, siis järeldub, et seeria (14) koondub kõikjal funktsioonile f(z). see ring ja mis tahes rõngas koondub seeria absoluutselt ja ühtlaselt sellele funktsioonile. Tõestame nüüd, et vormi (6) lagunemine on unikaalne. Oletame, et on veel üks laiendus, siis igal pool ringi R sees on Ringjoonel seeriad (15) koonduvad ühtlaselt. Korrutame võrdsuse mõlemad pooled (kus m on fikseeritud täisarv ja integreerime mõlemad seeriad termini kaupa. Selle tulemusena saame vasakul küljel ja paremal - Sch. Seega (4, = St. Kuna m on suvaline arv, viimane võrrand tõestab laienduse kordumatust.Seeriat (6), mille koefitsiendid arvutatakse valemite (7) abil, nimetatakse funktsiooni f(z) Laurent'i seeriaks ringis. selle seeria tingimuste komplekt nr negatiivsed jõud helistas õige osa Laurenti sari ja negatiivsetega - selle põhiosa. Laurenti seeria koefitsientide valemeid (7) kasutatakse praktikas harva, kuna reeglina nõuavad need tülikaid arvutusi. Tavaliselt kasutatakse võimalusel elementaarfunktsioonide Taylori valmis laiendusi. Dekompositsiooni unikaalsuse põhjal viib iga seaduslik meetod sama tulemuseni. Näide 2. Vaatleme Laurent'i seeria funktsioonide laiendusi erinevates piirkondades, eeldades, et Fuiscia /(r)-l on kaks ainsuse punkti: . Järelikult on kolm rõngakujulist piirkonda, mille keskpunkt on punktis r = 0. Igas neist on funktsioon f(r) analüütiline: a) ring on ring, ringi väliskülg (joonis 27). Leiame funktsiooni /(z) Laurent'i laiendused kõigis nendes piirkondades. Esitame /(z) elementaarmurdude summana a) Ring Teisendame seose (16) järgmiselt. Kasutades liikmete summa valemit geomeetriline progressioon, saame Asenda leitud laiendused valemiga (17): See laiendus on funktsiooni /(z) Taylori jada. b) Funktsiooni -r rõngas jääb selles rõngas konvergentseks, kuna funktsiooni j^j jaoks on seeria (19) |z| > 1 lahkneb. Seetõttu teisendame funktsiooni /(z) järgmiselt: rakendades jällegi valemit (19), saame, et See seeria koondub. Asendades laiendused (18) ja (21) relatsiooniga (20), saame c) funktsiooni -z ringi väliskülje |z| > 2 lahkneb ja seeria (21) funktsiooni jaoks - Esitame funktsiooni /(z) järgmisel kujul: /<*>Kasutades valemeid (18) ja (19), saame VÕI 1 See näide näitab, et sama funktsiooni f(z) korral on Laurent'i laiendus üldiselt erinevat tüüpi erinevatele rõngastele. Näide 3. Leia funktsiooni Laurent'i seeria 8. Laurent'i rea laiendus. Eraldatud ainsuse punktid ja nende klassifikatsioon ringipiirkonnas A Kasutame funktsiooni f(z) esitust järgmisel kujul: ja teisendame teise liikme Kasutades geomeetrilise progressiooni liikmete summa valemi saame Asendades leitud avaldised valemiga (22), saame näite 4. Laiendage funktsiooni Laurent'i seerias piirkonnas zq = 0. Iga kompleksi jaoks on meil Let This laienemine kehtib iga punkti z Ф 0 jaoks. Sel juhul esindab rõnga piirkond kogu komplekstasandit ühe kõrvale jäetud punktiga z - 0. Seda piirkonda saab defineerida järgmise seosega: See funktsioon on analüütiline piirkonnas Valemitest ( 13) Laurent'i seeria koefitsientide jaoks, kasutades sama põhjendust nagu eelmises lõigus, saab Kouiwi võrratused. kui funktsioon f(z) on piiratud ringiga, kus M on konstant), siis Eraldatud ainsuse punktid Punkti zo nimetatakse funktsiooni f(z) isoleeritud ainsuse punktiks, kui punktile ( seda hulka nimetatakse mõnikord punkti 2o punkteeritud naabruskonnaks, mille puhul funktsioon f(z) on kordumatu ja analüütiline. Punktis zo ise on funktsioon kas määratlemata või mitte üheselt mõistetav ja analüütiline. Sõltuvalt funktsiooni /(r) käitumisest punktile zo lähenemisel eristatakse kolme tüüpi ainsuse punkte. Eraldatud ainsuse punkti nimetatakse: 1) eemaldatavaks, kui on olemas lõplik 2) pmusach, kui 3) sisuliselt ainsuse punktiks, kui funktsioonil f(z) ei ole piirväärtust Isoleeritud ainsuse punkti tüüp on tihedalt seotud funktsiooni Laurent'i laiendamise olemus torgatud keskpunkti võrra. Teoreem 16. Funktsiooni f(z) isoleeritud ainsuse punkt z0 on eemaldatav ainsuse punkt siis ja ainult siis, kui funktsiooni f(z) Laurent'i laiend punkti zo naabruses ei sisalda põhiosa, st. on kujul Olgu zo eemaldatav ainsuse punkt. Siis on olemas lõplik, seega on funktsioon f(z) piiratud punkti z prokoloogilises naabruses. Panime Cauchy ebavõrdsuse tõttu Kuna p saab valida suvaliselt väikeseks, siis kõik koefitsiendid negatiivsetel astmetel (z) - 20) on võrdsed nulliga: vastupidi, olgu Laurent'il, et funktsiooni /(r) laiend punkti zq läheduses sisaldab ainult õiget osa, see tähendab, et sellel on vorm (23) ja seetõttu on see Taylor. On lihtne näha, et z -* z0 korral on funktsioonil /(z) piirväärtus: Teoreem 17. Funktsiooni f(z) isoleeritud ainsuse punkt zq on eemaldatav siis ja ainult siis, kui funktsioon J(z) on piirneb mõne punkti zq torgatud naabruskonnaga, Zgmechai mitte. Olgu r funktsiooni /(r) eemaldatav ainsuse punkt. Eeldades, et funktsioon /(r) on analüütiline mingis ringis, mille keskpunkt on punktis r. See määrab punkti nimetuse - eemaldatav. Teoreem 18. Funktsiooni f(z) isoleeritud ainsuse punkt zq on poolus siis ja ainult siis, kui funktsiooni f(z) Laurent'i laienduse põhiosa punkti läheduses sisaldab lõplikku (ja positiivset) arvu nullist erineva terminiga, st on kujul 4 Olgu z0 poolus. Sellest ajast alates on punkti z0 punkteeritud ümbrus, milles funktsioon f(z) on analüütiline ja nullist erinev. Seejärel määratletakse selles naabruses analüütiline funktsioon ja seetõttu on punkt zq funktsiooni eemaldatav ainsuse punkt (null) või kus h(z) on analüütiline funktsioon, h(z0) Φ 0. Siis h(zo) Φ 0 on samuti analüütiline, siis on funktsioon φ analüütiline punkti zq naabruses ja seetõttu, kust me saame selle Oletame nüüd, et funktsioonil f(z) on kuju (24) laiend punkti punkt zq läheduses. punkt zо. See tähendab, et selles naabruses on funktsioon f(z) koos funktsiooniga analüütiline. Funktsiooni g(z) puhul kehtib laiendus, millest on näha, et zq on funktsiooni g(z) eemaldatav ainsuse punkt ja eksisteerib Siis kipub 0-s olev funktsioon olema funktsiooni poolus. on veel üks lihtne fakt. Punkt Zq on funktsiooni f(z) poolus siis ja ainult siis, kui funktsiooni g(z) = yj saab laiendada analüütiliseks funktsiooniks punkti zq läheduses, seades g(z0) = 0. funktsiooni f(z) poolusest nimetatakse funktsiooni jfa nulljärku. 16. ja 18. teoreemist tuleneb järgmine väide. Teoreem 19. Eraldatud ainsuse punkt on sisuliselt ainsus siis ja ainult siis, kui Laurent'i laienduse põhiosa selle punkti punkteeritud naabruses sisaldab lõpmatult palju nullist erinevaid liikmeid. Näide 5. Funktsiooni ainsuse punkt on zo = 0. Meil on Laurent'i seeria isoleeritud ainsuse punktid ja nende klassifikatsioon Seetõttu on zo = O eemaldatav ainsuse punkt. Funktsiooni /(z) laiendus Laurent'i seeriaks nullpunkti läheduses sisaldab ainult õiget osa: Näide7. /(z) = Funktsiooni f(z) ainsuspunkt on zq = 0. Vaatleme selle funktsiooni käitumist reaal- ja imaginaarteljel: reaalteljel x 0, imaginaarteljel Järelikult on olemas ei ole f(z) lõplik ega lõpmatu piirväärtus z -* 0 ei eksisteeri. See tähendab, et punkt r = 0 on funktsiooni f(z) sisuliselt singulaarne punkt. Leiame funktsiooni f(z) Laurent'i laiendi nullpunkti lähedusest. Iga kompleksi C jaoks oleme seadnud. Siis sisaldab Laurent'i laiend lõpmatu arvu z negatiivse võimsusega liikmeid.
Kahe autonoomse diferentsiaalvõrrandi süsteemiga kirjeldatud mudelid.
Faasi tasapind. Faasportree. Isokliin meetod. Peamised isokliinid. Jätkusuutlikkus püsiseisund. Lineaarsed süsteemid. Ainsuse punktide tüübid: sõlm, sadul, fookus, keskpunkt. Näide: keemilised reaktsioonid esimene tellimus.
Kõige huvitavamad tulemused bioloogiliste süsteemide omaduste kvalitatiivse modelleerimise kohta saadi kahe diferentsiaalvõrrandi mudelite abil, mis võimaldavad kvalitatiivne uuring meetodit kasutades faasitasand. Vaatleme kahe autonoomse tavalise diferentsiaalvõrrandi süsteemi üldine vaade
(4.1)
P(x,y), Q(x,y)- pidevad funktsioonid, määratletud mõnes piirkonnas G Eukleidese tasapind ( x,y ‑ Descartes'i koordinaadid) ja millel on selles piirkonnas pidevad tuletised, mis ei ole madalamad kui esimene.
Piirkond G võib olla kas piiramatu või piiratud. Kui muutujad x, y omavad spetsiifilist bioloogilist tähendust (ainete kontsentratsioonid, liikide arv) kõige sagedamini piirkond G tähistab parempoolse pooltasandi positiivset kvadranti:
0 £ x< ¥ ,0 £ y< ¥ .
Ainete kontsentratsiooni või liikide arvu saab ülalt piirata ka laeva mahu või elupaiga pindalaga. Siis on muutujate vahemik järgmine:
0 £ x< x 0 , 0 £ y< y 0 .
Muutujad x, y aja muutumine vastavalt võrrandisüsteemile (4.1), nii et süsteemi iga olek vastab muutuja väärtuste paarile ( x, y).
|
|
 |
Ja vastupidi, iga muutujate paar ( x, y) vastab süsteemi teatud olekule.
Vaatleme koordinaattelgedega tasapinda, millele on joonistatud muutujate väärtused x,y. Iga punkt M see tasapind vastab süsteemi teatud olekule. Seda tasandit nimetatakse faasitasandiks ja see esindab süsteemi kõigi olekute kogumit. Punkti M(x,y) nimetatakse esindus- või esituspunktiks.
Laske esialgsel ajahetkel t=t 0 esinduspunkti koordinaate M 0 (x(t 0), y(t 0)). Igal järgmisel ajahetkel t esituspunkt nihkub vastavalt muutujate väärtuste muutustele x(t), y(t). Punktide kogumine M(x(t), y(t)) faasitasandil, mille asukoht vastab süsteemi olekutele muutujate ajas muutumise protsessis x(t), y(t) võrrandite (4.1) kohaselt nimetatakse faasi trajektoor.
Muutujate erinevate algväärtuste faasitrajektooride komplekt annab süsteemist kergesti nähtava "portree". Ehitus faasiportree võimaldab teha järeldusi muutujate muutuste olemuse kohta x, y teadmata algse võrrandisüsteemi analüütilisi lahendusi(4.1).
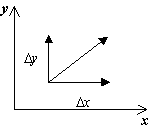
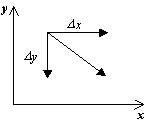
Faasiportree kujutamiseks on vaja faasitasandi igas punktis konstrueerida süsteemi trajektooride suundade vektorväli. Kasvu määramineD t>0,saame vastavad juurdekasvud D x Ja D y väljenditest:
D x=P(x,y)D t,
D y=Q(x,y)D t.
Vektori suund dy/dx punktis ( x, y) oleneb funktsioonide märgist P(x, y), Q(x, y) ja seda saab anda tabelina:
|
P(x,y)>0, Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
Selle võrrandi lahendus y = y(x,c), või kaudselt F(x,y)=c, Kus Koos– integratsioonikonstant, annab võrrandi (4.2) integraalkõverate perekonna – faasi trajektoorid süsteem (4.1) lennukis x, y.
Isokliinne meetod
Nad kasutavad faasiportree konstrueerimiseks isokliini meetod - faasitasandile tõmmatakse jooned, mis lõikuvad integraalkõverad ühe kindla nurga all. Isookliini võrrandi on lihtne saada punktist (4.2). Paneme
Kus A– teatud konstantne väärtus. Tähendus A tähistab puutuja kaldenurga puutujat faasitrajektoorile ja võib võtta väärtusi alates –¥ kuni + ¥ . Selle asemel asendamine dy/dx punktis (4.2) kogus A saame isokliini võrrandi:
.(4.3)
Võrrand (4.3) määrab tasandi igas punktis vastava integraalkõvera kordumatu puutuja, välja arvatud punkt, kus P(x,y)= 0, Q (x,y) = 0 , milles puutuja suund muutub ebakindlaks, kuna tuletise väärtus muutub ebakindlaks:
.
See punkt on kõigi isokliinide lõikepunkt - eriline punkt. Selles kaovad muutujate ajatuletised samaaegselt x Ja y.
Seega on ainsuse punktis muutujate muutumise kiirused null. Järelikult vastab faasitrajektooride (4.2) diferentsiaalvõrrandite ainsuspunkt süsteemi statsionaarne olek(4.1) ja selle koordinaadid on muutujate statsionaarsed väärtused x, y.
Erilist huvi pakuvad peamised isokliinid:
dy/dx=0, P(x,y)=0 – horisontaalsete puutujate isokliin ja
dy/dx=¥ ,Q(x,y)=0 – vertikaalsete puutujate isokliin.
Konstrueerides peamised isokliinid ja leides nende lõikepunkti (x,y), mille koordinaadid vastavad järgmistele tingimustele:
leiame seeläbi faasitasandi kõigi isokliinide lõikepunkti, milles faasitrajektooride puutujate suund on ebakindel. see - ainsuse punkt, mis vastab süsteemi statsionaarne olek(joonis 4.2).
Süsteemil (4.1) on nii palju statsionaarseid seisundeid, kui palju on faasitasandil peamiste isokliinide lõikepunkte.
Iga faasitrajektoor vastab dünaamilise süsteemi liikumiste kogumile, mis läbib samu olekuid ja erinevad üksteisest ainult ajalugemise alguses.
 |
|
Kui Cauchy teoreemi tingimused on täidetud, siis läbi iga ruumipunkti x, y, t on ainult üks integraalkõver. Sama kehtib autonoomia tõttu faasitrajektooride puhul: faasitasandi iga punkti läbib ühefaasiline trajektoor.
Stabiilsus püsiolekus
Olgu süsteem tasakaaluseisundis.
Siis asub esinduspunkt süsteemi ühes ainsuse punktis, kus definitsiooni järgi:
.
Selle, kas ainsuse punkt on stabiilne või mitte, määrab see, kas esinduspunkt lahkub väikese kõrvalekaldega statsionaarsest olekust või mitte. Seoses kahe võrrandi süsteemiga stabiilsuse määratlus keelese, djärgnevalt.
Tasakaaluseisund on stabiilne, kui tasakaaluolekust mis tahes kõrvalekallete vahemikus (e )saate piirkonna täpsustada d (e ), mis ümbritseb tasakaaluolekut ja millel on omadus, et piirkonnast ei alga trajektoori d , ei jõua kunagi piirini e . (Joonis 4.4)
 |
|
Suure süsteemide klassi jaoks - töötlemata süsteemid – kelle käitumise olemus ei muutu võrrandite kuju väikesel muutusel, saab infot käitumistüübi kohta statsionaarse oleku läheduses, uurides mitte algset, vaid lihtsustatud lineariseeritud süsteem.
Lineaarsed süsteemid.
Mõelge kahele süsteemile lineaarvõrrandid:
.(4.4)
Siin a, b, c, d- konstandid, x, y- Descartes'i koordinaadid faasitasandil.
Otsime üldist lahendust kujul:
.(4.5)
Asendame need avaldised (4.4) ja vähendame võrra e l t:
(4.6)
Algebraline võrrandisüsteem (4.6) tundmatutega A, B on nullist erinev lahendus ainult siis, kui selle tundmatute koefitsientidest koosnev determinant on võrdne nulliga:
.
Laiendades seda determinanti, saame süsteemile iseloomuliku võrrandi:
.(4.7)
Selle võrrandi lahendamine annab eksponendi väärtusedl 1,2 , mille jaoks on võimalikud nullist erinevad väärtused A Ja B võrrandi (4.6) lahendid. Need tähendused on
.(4.8)
Kui radikaalavaldis on negatiivne, siisl 1,2 kompleksarvud. Oletame, et võrrandi (4.7) mõlemal juurtel on nullist erinevad reaalosad ja mitu juurt pole olemas. Siis saab süsteemi (4.4) üldlahendust esitada eksponentsiaalide ja eksponentide lineaarse kombinatsiooninal 1 , l 2 :
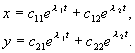(4.9)
Süsteemi võimalike trajektooride olemuse analüüsimiseks faasitasandil kasutame lineaarne homogeenne koordinaatide teisendus, mis viib süsteemi kanooniline vorm:
,(4.10)
võimaldades algse süsteemiga (4.4) võrreldes mugavamat esitust faasitasandil. Tutvustame uusi koordinaateξ , η vastavalt valemitele:
(4.1)
Lineaaralgebra käigust on teada, et ebavõrdsuse korral nullida reaalosadl 1 , l 2 algsüsteemi (4.4) saab alati teisendada teisenduste (4.11) abil kanooniliseks vormiks (4.10) ja uurida selle käitumist faasitasandilξ , η . Vaatleme erinevaid juhtumeid, mis võivad siin esineda.
Juured λ 1 , λ 2 – kehtiv ja sama märgiga
Sel juhul on teisenduskoefitsiendid reaalsed, liigume reaaltasandiltx,yreaaltasandile ξ, η. Jagades teise võrrandi (4.10) esimesega, saame:
.(4.12)
Selle võrrandi integreerimisel leiame:
Kus .(4.13)
Leppigem kokku, et mõistame λ järgi 2 suure mooduliga tunnusvõrrandi juur, mis ei riku meie arutluskäigu üldistust. Siis, kuna vaadeldaval juhul juured λ 1 , λ 2 – kehtiv ja sama tähisega,a>1 , ja me käsitleme paraboolset tüüpi integraalkõveraid.
Kõik integraalkõverad (välja arvatud telg η , mis vastab ) puudutage telje alguspunkti ξ, mis on ühtlasi võrrandi (4.11) integraalkõver. Koordinaatide alguspunkt on eriline punkt.
Nüüd selgitame välja esinduspunkti liikumissuuna piki faasitrajektoore. Kui λ 1, λ 2 on negatiivsed, siis, nagu on näha võrranditest (4.10), |ξ|, |η| väheneb aja jooksul. Esinduspunkt läheneb koordinaatide alguspunktile, kuid ei jõua kunagi selleni. Vastasel juhul oleks see vastuolus Cauchy teoreemiga, mis väidab, et faasitasandi igat punkti läbib ainult üks faasitrajektoor.
Selline eriline punkt, mida läbivad integraalkõverad, nagu paraboolide perekond 
läbib alguspunkti ja seda nimetatakse sõlmeks (joonis 1). 4.5)
Sõlmetüübi tasakaaluseisund λ juures 1, λ 2 < 0 on Ljapunov stabiilne, kuna esituspunkt liigub mööda kõiki integraalkõveraid koordinaatide alguspunkti suunas. See stabiilne sõlm. Kui λ 1, λ 2 > 0 siis |ξ|, |η| aja jooksul suurenevad ja esinduspunkt eemaldub koordinaatide alguspunktist. Sel juhul eripunkt– ebastabiilne sõlm .
Faasitasandil x, y integraalkõverate käitumise üldine kvalitatiivne olemus säilib, kuid integraalkõverate puutujad ei kattu koordinaatide telgedega. Nende puutujate kaldenurk määratakse koefitsientide suhtega α , β , γ , δ võrrandites (4.11).
Juured λ 1 , λ 2 – kehtivad ja erineva märgiga.
Teisenda alates koordinaadid x,y koordinaatidele ξ, η jälle tõeline. Kanooniliste muutujate võrrandid on jälle kujul (4.10), kuid nüüd on λ märgid 1, λ 2 on erinevad. Faasitrajektooride võrrandil on vorm:
Kus , (4.14)
Integreerides (4.14), leiame
(4.15)
See võrrand määratleb hüperboolset tüüpi kõverate perekonna, kus mõlemad koordinaatteljed- asümptoodid (at a=1 meil oleks võrdkülgsete hüperboolide perekond). Koordinaatide teljed on sel juhul samuti integraalkõverad– need on ainsad integraalkõverad, mis läbivad alguspunkti. Igamillest koosneb kolmest faasitrajektoorist: kahest liikumisest tasakaaluseisundisse (või tasakaaluseisundist) ja tasakaaluseisundist. Kõik muud integraalkõverad– on hüperboolid, mis ei läbi alguspunkti (joon. 4.6) Seda erilist punkti nimetatakse "sadul ». Mäesadula lähedal olevad tasapinnad käituvad sarnaselt sadula läheduses olevate faasitrajektooridega.
Vaatleme esinduspunkti liikumise olemust mööda faasitrajektoore tasakaaluoleku lähedal. Olgu näiteksλ 1 > 0, λ 2<0 . Seejärel asetatakse teljele esinduspunkt ξ , eemaldub lähtepunktist ja asetatakse teljele η – läheneb lõputult koordinaatide alguspunktile, jõudmata selleni piiratud aja jooksul. kus iganes esituspunkt alghetkel asub (välja arvatud ainsuse punkt ja asümptoodi punktid η =0), see liigub lõpuks tasakaaluolekust eemale, isegi kui see liigub alguses piki üht integraalkõverat ainsuse punkti suunas.
See on ilmne ainsuse punkt, näiteks sadul, on alati ebastabiilne . Ainult spetsiaalselt valitud algtingimustel asümptoodilη =0 süsteem läheneb tasakaaluseisundile. See aga ei ole vastuolus väitega süsteemi ebastabiilsuse kohta. Kui loeme, et kõik süsteemi algseisundid faasitasandil on võrdselt tõenäolised, siis sellise algseisundi tõenäosus, mis vastab liikumisele suunas To ainsuse punkt on võrdne nulliga. Seetõttu viib iga reaalne liikumine süsteemi tasakaaluseisundist välja.Koordinaatide juurde tagasi minnesx,y,saame sama kvalitatiivse pildi trajektooride liikumise olemusest ümber koordinaatide alguspunkti.
Sõlme ja sadula vaadeldavate juhtumite vaheline piir on juhtum Millal näiteks üks iseloomulikest näitajatest λ 1 , kaob, mis tekib siis, kui süsteemi determinant- väljendus ad-bc=0(vt valem 4.8 ). Sel juhul on võrrandite (4.4) paremate külgede koefitsiendid üksteisega võrdelised:
ja süsteemi tasakaaluolekud on kõik sirge punktid:
Ülejäänud integraalkõverad on nurkkoefitsiendiga paralleelsete sirgjoonte perekond , mida mööda esinduspunktid kas lähenevad tasakaaluseisundile või eemalduvad sellest, olenevalt karakteristiku võrrandi λ teise juure märgist 2 = a+d.(Joonis 4. 7 ) Sel juhul sõltuvad tasakaaluseisundi koordinaadid muutujate algväärtusest.
Juured λ 1 , λ 2 – keerulinekonjugaat
Sel juhul päriseltx Ja y me teeme omavad keerukaid konjugaate ξ , η (4.10) . Teise vaheteisenduse sisseviimisega on aga võimalik ka sel juhul taandada arvestamine tõeliseks lineaarseks homogeenseks teisenduseks. Paneme:
(4.16)
Kus a,b, Ja u,v – tegelikud väärtused. Võib näidata, et teisendus alatesx,y To u,v on meie eelduste kohaselt reaalne, lineaarne, homogeenne, mille determinant erineb nullist. Võrrandite tõttu(4.10, 4.16) meil on:
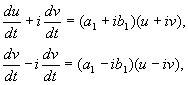
kus
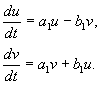(4.17)
Võrrandi teise jagamine esimesega, saame:
mida on lihtsam integreerida, kui läheme polaarkoordinaatide süsteemi (r, φ ) . Pärast asendamist me saame kust:
.(4.18)
Seega faasitasandilu, vmeil on tegemist logaritmiliste spiraalide perekonnaga, millest igaühel onasümptootiline punkt päritolus.Ainsuspunkt, mis on kõigi spiraalikujuliste integraalkõverate asümptootiline punkt, pesastatud igassesõber, seda nimetatakse keskenduda ( Joon.4.8 ) .
Vaatleme esinduspunkti liikumise olemust mööda faasitrajektoore. Esimese võrrandi (4.17) korrutamineu, ja teine sisse v ja lisades saame:
Kus
Lase a 1 < 0 (a 1 = Reλ ) . Esinduspunkt läheneb seejärel pidevalt koordinaatide alguspunktile, jõudmata selleni piiratud aja jooksul. See tähendab, et faasitrajektoorid on keerdspiraalid ja vastavad summutatud võnkudele muutujad. see - püsiv fookus .
Stabiilse fookuse korral, nagu ka stabiilse sõlme puhul, pole täidetud mitte ainult Ljapunovi tingimus, vaid ka rangem nõue. Nimelt naaseb süsteem mistahes esialgsete kõrvalekallete korral aja jooksul tasakaaluasendile soovitud lähedale. Sellist stabiilsust, mille puhul alghälbed mitte ainult ei suurene, vaid ka lagunevad, kaldudes nulli, nimetatakse absoluutne stabiilsus .
Kui valemis (4.18) a 1 >0 , siis esinduspunkt eemaldub lähtepunktist ja meil on tegemist ebastabiilne fookus . Lennukilt liikudesu,vfaasitasandilex, yspiraalid jäävad samuti spiraalideks, aga deformeeruvad.
Vaatleme nüüd juhtumit, mila 1
=0
. Faasi trajektoorid lennukisu, vtulevad ringid 
mis lennukisx,yvastavad ellipsile:
Seega, millala 1=0 spetsiaalse punkti kaudux= 0, y= 0 ükski integraalkõver ei läbi. Sellist isoleeritud ainsuspunkti, mille lähedal integraalkõverad on suletud kõverad, eelkõige üksteise sisse põimitud ja ainsuse punkti ümbritsevad ellipsid, nimetatakse keskpunktiks.
Seega on võimalikud kuut tüüpi tasakaaluseisundid, olenevalt karakteristliku võrrandi (4.7) juurte olemusest. Vaade faasitrajektooridele tasapinnal x, y nende kuue juhtumi puhul on näidatud joonisel fig. 4.9.
Riis. 4.9.Faasportreede tüübid statsionaarse oleku läheduses lineaarvõrrandisüsteemi jaoks (4.4).
Viit tüüpi tasakaaluseisundit on jämedad, nende iseloom ei muutu võrrandite (4.4) parempoolsete külgede piisavalt väikeste muutuste korral. Sel juhul peaksid muudatused mitte ainult paremates külgedes, vaid ka nende esimest järku tuletis olema väikesed. Kuues tasakaaluseisund – keskpunkt – ei ole konarlik. Väikeste muudatustega võrrandite parema poole parameetrites muutub see stabiilseks või ebastabiilseks fookuseks.
Bifurkatsiooniskeem
Tutvustame järgmist tähistust:
.
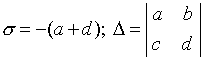(4.11)
Seejärel kirjutatakse iseloomulik võrrand järgmiselt:
.
(4.12)
Vaatleme ristkülikukujuliste ristkülikukujuliste koordinaatidega tasapinda s , D ja märgi sellele alad, mis vastavad üht või teist tüüpi tasakaaluseisundile, mille määrab karakteristiku võrrandi juurte olemus
.(4.13)
Tasakaaluseisundi stabiilsuse tingimuseks on y negatiivse reaalosa olemasolul 1 ja l 2 . Selle vajalik ja piisav tingimus on ebavõrdsuse täitumines > 0, D > 0 . Diagrammil (4.15) vastab see tingimus punktidele, mis asuvad parameetritasandi esimeses veerandis. Ainsuse punkt on fookus, kuil 1 ja l 2 keeruline. See tingimus vastab nendele tasapinna punktidele, mille jaoks , need. punktid parabooli kahe haru vahels 2 = 4 D. Teljepunktid s = 0, D>0, vastavad tsentri tüüpi tasakaaluolekutele. Samamoodil 1 ja l 2 - kehtivad, kuid erineva märgiga, s.t. ainsuse punkt on sadul, kui D<0, jne. Selle tulemusena saame parameetritasandi jaotuse diagrammi s, D, piirkondadeks, mis vastavad erinevat tüüpi tasakaaluolekutele.
Riis. 4.10. Bifurkatsiooniskeem
lineaarvõrrandisüsteemi jaoks 4.4
Kui lineaarsüsteemi koefitsiendid a, b, c, d sõltuvad teatud parameetrist, siis kui see parameeter muutub, muutuvad ka väärtuseds , D . Piiride ületamisel muutub faasiportree iseloom kvalitatiivselt. Seetõttu nimetatakse selliseid piire bifurkatsioonipiirideks – piiri vastaskülgedel on süsteemil kaks topoloogiliselt erinevat faasiportreed ja vastavalt sellele ka kaks erinevat tüüpi käitumist.
Diagramm näitab, kuidas sellised muutused võivad toimuda. Kui välistada erijuhud - koordinaatide alguspunkt -, siis on hästi näha, et sadul võib ordinaattelje ületamisel muutuda sõlmeks, stabiilseks või ebastabiilseks. Stabiilne sõlm võib minna kas sadulasse või stabiilsesse fookusesse jne. Pange tähele, et üleminekud stabiilne sõlm - stabiilne fookus ja ebastabiilne sõlm - ebastabiilne fookus ei ole bifurkatsioonid, kuna faasiruumi topoloogia ei muutu. Faasiruumi topoloogiast ja bifurkatsiooniüleminekutest räägime lähemalt 6. loengus.
Bifurkatsioonisiirde ajal muutub ainsuse punkti stabiilsuse olemus. Näiteks stabiilne fookus läbi keskpunkti võib muutuda ebastabiilseks fookuseks. Seda bifurkatsiooni nimetatakse Andronov-Hopfi bifurkatsioon seda uurinud teadlaste nimede järgi. Selle bifurkatsiooni käigus mittelineaarsetes süsteemides sünnib piirtsükkel ja süsteem muutub isevõnkuvaks (vt loeng 8).
Näide. Lineaarne keemilise reaktsiooni süsteem
Aine X voolab väljast püsiva kiirusega, muutub aineks Y ja aine kontsentratsiooniga võrdelise kiirusega Y, eemaldatakse reaktsioonisfäärist. Kõik reaktsioonid on esimest järku, välja arvatud aine sissevool väljastpoolt, mis on nulljärku. Reaktsiooniskeem näeb välja selline:
(4.14)
ja seda kirjeldab võrrandisüsteem:
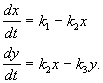(4.15)
Statsionaarsed kontsentratsioonid saame, võrdsustades parempoolsed küljed nulliga:
.(4.16)
Vaatleme süsteemi faasiportreed. Jagame süsteemi (4.16) teise võrrandi esimesega. Saame:
.(4.17)
Võrrand (4.17) määrab muutujate käitumise faasitasandil. Ehitame selle süsteemi faasiportree. Kõigepealt joonistame faasitasandile peamised isokliinid. Vertikaalsete puutujate isokliini võrrand:
Horisontaalsete puutujate isokliini võrrand:
Ainsuse punkt (statsionaarne olek) asub peamiste isokliinide ristumiskohas.
Nüüd teeme kindlaks, millise nurga all lõikuvad koordinaatteljed integraalkõveratega.
Kui x= 0, siis.
Seega integraalkõverate puutuja puutuja y=y(x), ristuvad ordinaatteljega x=0, on ülemisel pooltasandil negatiivne (pidage meeles, et muutujad x, y neil on kontsentratsiooni väärtused ja seetõttu huvitab meid ainult faasitasandi ülemine parem kvadrant). Sellisel juhul suureneb puutuja nurga puutuja koos kaugusega alguspunktist.
Mõelge teljele y= 0. Punktis, kus see telg lõikab integraalkõveraid, kirjeldatakse neid võrrandiga
Kell abstsisstelge ületavate integraalkõverate kalde puutuja on positiivne ja suureneb suurenedes nullist lõpmatuseni x.
Kell .
Seejärel väheneb kaldenurga puutuja absoluutväärtuses edasise suurenemisega, jäädes negatiivseks ja kaldub väärtusele -1 x ® ¥ . Teades integraalkõverate puutujate suunda põhiisokliinidel ja koordinaatide telgedel, on lihtne koostada faasitrajektooride tervikpilti.
 |
|
Teeme kindlaks ainsuse punkti stabiilsuse olemuse Ljapunovi meetodi abil. Süsteemi iseloomulik determinant on kujul:
.
Laiendades determinanti, saame süsteemile iseloomuliku võrrandi: , st. Iseloomuliku võrrandi juured on mõlemad negatiivsed. Järelikult on süsteemi statsionaarne olek stabiilne sõlm. Sel juhul aine kontsentratsioon X kaldub statsionaarsesse olekusse alati monotoonselt, aine Y kontsentratsioon võib läbida min või max. Võnkumisrežiimid on sellises süsteemis võimatud.
Ainus punkt matemaatikas. 1) kõvera ainsuspunkt, mis on määratletud võrrandiga F ( x, y) = 0, - punkt M 0 ( x 0, y 0), milles funktsiooni F () mõlemad osatuletised x, y) minge nulli: Kui mitte kõik funktsiooni F () teised osatuletised x, y) punktis M 0 on võrdsed nulliga, siis nimetatakse O. t kahekordseks. Kui koos punktis M0 kaduvate esimeste tuletistega kaovad kõik teised, kuid mitte kõik kolmandad tuletised, siis nimetatakse võrrandit kolmikuks jne. Kahekordse O.t. lähedal asuva kõvera struktuuri uurimisel on avaldise märgil oluline roll Kui Δ > 0, siis nimetatakse avatud ruumi isoleeritud; näiteks kõvera juures y 2 - x 4 + 4x 2= 0 koordinaatide alguspunkt on isoleeritud O. t. (vt. riis. 1
). Kui Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 koordinaatide alguspunkt on sõlm O. t. (vt. riis. 2
). Kui Δ = 0, siis on kõvera üldpunkt kas isoleeritud või seda iseloomustab asjaolu, et kõvera erinevatel harudel on selles punktis ühine puutuja, näiteks: a) 1. tüüpi harupunkt - kõvera erinevad harud. kõverad asuvad ühise puutuja vastaskülgedel ja moodustavad punkti, nagu kõver a 2 - x 3= 0 (vt riis. 3
, a); b) 2. tüüpi tipppunkt - kõvera erinevad harud asuvad ühel pool ühist puutujat, nagu kõver
(y – x 2)2-x5= 0 (vt riis. 3
, b); c) isepuutepunkt (kõvera jaoks a 2 - x 4= 0 alguspunkt on enesepuutepunkt; (cm. riis. 3
, V). Koos märgitud O. t-ga on palju teisi erinimedega O. t; Näiteks asümptootiline punkt on lõpmatu arvu pööretega spiraali tipp (vt. riis. 4
), lõpp-punkt, nurgapunkt jne. 2) Diferentsiaalvõrrandi ainsuspunkt on punkt, kus diferentsiaalvõrrandi parema külje lugeja ja nimetaja samaaegselt kaovad (vt Diferentsiaalvõrrandid) kus P ja Q on pidevalt diferentseeruvad funktsioonid. Eeldades, et O. t. asub koordinaatide alguspunktis ja kasutades Taylori valemit (vt Taylori valemit), saame võrrandit (1) esitada kujul kus P 1 ( x, y) ja Q 1 ( x, y) – suhtes lõpmata väike Nimelt, kui λ 1 ≠ λ 2 ja λ 1 λ 2 > 0 või λ 1 = λ 2, siis O. t. on sõlm; sinna sisenevad kõik integraalkõverad, mis läbivad sõlme piisavalt väikese naabruskonna punkte. Kui λ 1 ≠ λ 2 ja λ 1 λ 2 i β, α ≠ 0 ja β ≠ 0, siis on üldpunkt fookus; kõik integraalkõverad, mis läbivad punkte fookuse piisavalt väikeses naabruses, kujutavad endast lõpmatu arvu pööretega spiraale mis tahes suvaliselt väikeses fookuse ümbruses. Kui lõpuks λ 1,2 = ± iβ, β ≠ 0, siis O. t iseloomu ei määra P () laiendustes ainult lineaarsed liikmed. x, y) ja Q ( x, y), nagu juhtus kõigil ülalnimetatud juhtudel; siin võib O. t. olla fookus või keskus või olla rohkem keeruline iseloom. Keskuse läheduses on kõik integraalkõverad suletud ja sisaldavad keskpunkti enda sees. Näiteks punkt (0, 0) on võrrandite sõlm juures" = 2u/x(λ 1 = 1, λ 2 = 2; vt riis. 5
, a) ja y" = u/x(λ 1 = λ 2 = 1; vt riis. 5
, b), võrrandi sadul y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. riis. 6
), võrrandi fookus y" =(x + y) /
(x - y) (λ 1 = 1 - i, λ 2 = 1 + i; cm. riis. 7
) ja võrrandi keskpunkt y" = -x/y(λ 1 = -i, λ 2 = i; cm. riis. 8
). Kui x, y) ja Q ( x, y) analüütiline, naabruskond O. t. kõrgem järjekord saab jagada piirkondadeks: D 1 - täidetud integraalkõveratega, mõlemad otsad sisalduvad O. t.-s (elliptilised piirkonnad), D 2 - täis integraalkõveratega, üks ots sisaldub O. t.-s (paraboolsed piirkonnad), ja D 3 - piirkonnad , mis on piiratud kahe üldteoorias sisalduva integraalkõveraga, mille vahel paiknevad hüperbooli tüüpi integraalkõverad (hüperboolsed piirkonnad) (vt. riis. 9
). Kui üldpunktis ei ole integraalkõveraid, siis nimetatakse üldpunkti stabiilset tüüpi punktiks. Stabiilse ostsillaatori ümbrus koosneb suletud integraalkõveratest, mis sisaldavad endas osmoosi ja mille vahel on spiraalid (vt joonis 1). riis. 10
). Diferentsiaalvõrrandite uurimine, st sisuliselt diferentsiaalvõrrandite naabruses olevate integraalkõverate perekondade käitumise uurimine, moodustab diferentsiaalvõrrandite kvalitatiivse teooria ühe haru ja mängib olulist rolli rakendustes, eriti liikumise stabiilsuse küsimused (A. M. Ljapunovi, A. Poincaré jt teosed). 3) Ühe väärtusega analüütilise funktsiooni ainsuse punkt on punkt, kus funktsiooni analüütilisust rikutakse (vt Analüütilised funktsioonid). Kui on naabruskond O. t. a, vaba teistest O. t., siis punkt A nimetatakse isoleeritud O. t. Kui A- isoleeritud üldteooria ja on olemas lõplik a, nimetatakse eemaldatavaks üldteooriaks. Muutes sobivalt funktsiooni definitsiooni punktis a (või defineerides selle uuesti selles punktis, kui selles olev funktsioon pole üldse defineeritud) nimelt oletades f(a)= b, on seda võimalik saavutada a muutub parandatud funktsiooni tavaliseks punktiks. Näiteks punkt z= 0 on eemaldatav O. t. funktsiooni f 1 ( z) = f(z), Kui z≠ 0 ja f 1 (0), = 1, punkt z= 0 on tavaline punkt [ f 1 (z) on punktis analüütiline z= 0]. Kui A- isoleeritud O. t. ja a nimetatakse funktsiooni pooluseks või sisuliselt ainsuse punktiks f(z), kui Laurenti seeria) toimib f(z) isoleeritud O. t läheduses ei sisalda negatiivseid võimeid z - a, Kui A- eemaldatav O. t., sisaldab piiratud arvu negatiivseid kraade z - a, Kui A- poolus (antud juhul masti järjekord R defineeritud kui kõrgeim aste a on sisuliselt ainsuse punkt. Näiteks funktsiooni jaoks punkt z= 0 on järjekorra poolus R, funktsiooni jaoks punkt z= 0 on sisuliselt ainsuse punkt. Astumusrea konvergentsiringi piiril peab olema vähemalt üks O.t funktsioonist, mida selles ringis andmed esindavad jõuseeria. Kõik ainulaadse analüütilise funktsiooni (loodusliku piiri) olemasolu valdkonna piiripunktid on selle funktsiooni piirid. Seega kõik ühikringi punktid | z| = 1 on funktsiooni jaoks erilised Mitme väärtusega analüütilise funktsiooni puhul kasutatakse kontseptsiooni „O. T." keerulisem. Funktsiooni Riemanni pinna üksikutel lehtedel (ehk üheväärtuslike analüütiliste elementide O. t.) on lisaks O. t-le iga hargnemispunkt ka funktsiooni O. t. Riemanni pinna eraldatud hargnemiskohad (st sellised hargnemiskohad, mille mõnes naabruses pole üheski lehes muid O. t. funktsioone) liigitatakse järgmiselt. Kui a on lõpliku järjestusega isoleeritud hargnemispunkt ja on olemas lõplik a, nimetatakse seda kriitiliseks pooluseks. Kui A- lõpmatu järjestusega isoleeritud hargnemispunkti ja a nimetatakse transtsendentaalseks O.t. Kõiki teisi isoleeritud hargnemispunkte nimetatakse kriitilisteks sisuliselt ainsuse punktideks. Näited: punkt z= 0 on funktsiooni f ( z) = log z ja funktsiooni kriitiline sisuliselt ainsuse punkt f (z) = sin ln z. Iga üldprobleem, välja arvatud eemaldatav, on takistuseks analüütilisele jätkamisele, st analüütiline jätkamine mööda taandamatut üldprobleemi läbivat kõverat on võimatu. Suur Nõukogude entsüklopeedia. - M.: Nõukogude entsüklopeedia.
1969-1978
.
p = 2, 3, …)
Vaadake, mis on "ainsuse punkt" teistes sõnaraamatutes:
Punktid siin. Vaata ka ainsuse punkti ( diferentsiaalvõrrandid). Tunnus või singulaarsus on matemaatikas punkt, kus matemaatiline objekt (tavaliselt funktsioon) on määratlemata või ebakorrapärase käitumisega (näiteks punkt, kus ... ... Wikipedia
Analüütiline funktsioon on punkt, kus analüütilisuse tingimusi rikutakse. Kui analüütiline funktsioon f(z) on antud punkti z0 teatud läheduses igal pool... Füüsiline entsüklopeedia
Analüütiline funktsioon on punkt, kus funktsiooni analüütilisust rikutakse... Suur entsüklopeediline sõnaraamat
ainsuse punkt- - [Ja.N.Luginski, M.S.Fezi Žilinskaja, Ju.S.Kabirov. Inglise-vene elektrotehnika ja energeetika sõnaraamat, Moskva, 1999] Elektrotehnika teemad, põhimõisted ET ainsus ... Tehniline tõlkija juhend
1) Analüütiline funktsioon f(z) on takistuseks kompleksmuutuja z funktsiooni f(z) elemendi analüütilisele jätkumisele piki selle muutuja tasapinna mis tahes teed. Olgu analüütiline funktsioon f(z) defineeritud mõne... ... Matemaatiline entsüklopeedia
Analüütiline funktsioon, punkt, kus funktsiooni analüütilisust rikutakse. * * * SINGLE POINT Analüütilise funktsiooni ÜKS PUNK, punkt, kus funktsiooni analüütilisust rikutakse... entsüklopeediline sõnaraamat
ainsuse punkt- ypatingasis taškas statusas T ala automatika vastavusmenys: engl. ainsuse punkt vok. singulärer Punkt, m rus. ainsuse punkt, f pranc. punktosake, m; point singulier, m … Automatikos terminų žodynas
ainsuse punkt- ypatingasis taškas statusas T ala fizika atitikmenys: engl. ainsuse punkt vok. singulärer Punkt, m rus. ainsuse punkt, f pranc. point singulier, m … Fizikos terminų žodynas
Põhimõisted ja määratlused:
Analüütilise funktsiooni f(z) null on punkt “a”, mille puhul f(a)=0.
Funktsiooni f(z) järgu “n” null on punkt “a”, kui fn(a)¹0.
Ainsuse punkti “a” nimetatakse funktsiooni f(z) isoleeritud ainsuse punktiks, kui selle punkti naabruses pole peale “a” ainsuse punkte.
Eraldatud ainsuse punkte on kolme tüüpi: .
1 eemaldatav ainsuspunkt;
3 sisuliselt ainsuse punkti.
Singulaarpunkti tüübi saab määrata antud funktsiooni käitumise põhjal leitud ainsuse punktis, aga ka leitud ainsuse punkti naabruses oleva funktsiooni jaoks saadud Laurent'i seeria kuju järgi.
Ainsuse punkti tüübi määramine selles oleva funktsiooni käitumise järgi.
1. Eemaldatavad ainsuse punktid.
Funktsiooni f(z) isoleeritud ainsuse punkti a nimetatakse eemaldatavaks, kui on olemas lõplik piir.
2.Poolakad.
Funktsiooni f(z) isoleeritud ainsuse punkti a nimetatakse pooluseks, kui 
.
3. Sisuliselt ainsuse punktid.
Funktsiooni f(z) isoleeritud ainsuse punkti a nimetatakse sisuliselt ainsuse punktiks, kui ei eksisteeri ei lõplikku ega lõpmatut.
Funktsiooni nullide ja pooluste vahel on järgmine seos.
Selleks, et punkt a oleks funktsiooni f(Z) järgu n poolus, on vajalik ja piisav, et see punkt oleks funktsiooni n järku null.
Kui n=1, nimetatakse poolust lihtsaks.
Definitsioon: Eraldatud ühemõttelise olemusega ainsuse punkti nimetatakse:
a) eemaldatav, kui lagunemise põhiosa puudub;
b) poolus, kui põhiosas on lõplik arv termineid;
c) sisuliselt ainsuse punkt, kui põhiosa sisaldab lõpmatu arvu termineid.
a) Seega on eemaldatava ainsuse punkti läheduses laiendus järgmine:
see väljendab funktsiooni ringi kõigis punktides |z-a| Keskmes z=a võrdsus ei ole tõene, sest funktsioonil z=a on katkestus ja parem pool on pidev. Kui keskmes oleva funktsiooni väärtust muuta, võttes selle võrdseks parempoolse külje väärtusega, siis tühimik elimineeritakse – sellest ka nimi – eemaldatav. b) M järku pooluse läheduses on Laurent'i seeria laiendus järgmine: c) Lihtposti läheduses Mahaarvamised ja nende arvutamise valemid. Analüütilise funktsiooni f(z) jääk isoleeritud ainsuse punktis z 0 on kompleksarv, mis on võrdne integraali väärtusega Funktsiooni f(z) jääki isoleeritud ainsuse punktis z 0 tähistatakse sümboliga Res f(z 0) või Res (f(z); z 0). Seega Res f(z 0)= Kui paneme valemisse (22.15.1) n=-1, saame: C-1 = või Res f(z 0) = C-1, need. funktsiooni f(z) jääk ainsuse punkti z 0 suhtes on võrdne Laurent'i rea funktsiooni f(z) laienduses oleva esimese negatiivse eksponendiga liikme koefitsiendiga. Mahaarvamiste arvutamine. Regulaarsed või eemaldatavad üksikud punktid. Ilmselgelt, kui z=z 0 on funktsiooni f(z) korrapärane või eemaldatav ainsuse punkt, siis Res f(z 0)=0 (sel juhul puudub Laurent'i laiendusel põhiosa, seega c-1=0) . Poolakas. Olgu punkt z 0 funktsiooni f(z) lihtpoolus. Siis on Laurent'i seeria funktsiooni f(z) jaoks punkti z 0 läheduses kujul: Siit Seega, kui ületame selle võrdsuse piirini z --z 0, saame Res f(z0)= Sisuliselt eriline punkt. Kui punkt z 0 on funktsiooni f(z) sisuliselt ainsuse punkt, siis funktsiooni jäägi arvutamiseks selles punktis määratakse funktsiooni Laurent'i seeria laienduses tavaliselt otseselt koefitsient c-1. Sündmuste klassifikatsioon. Sündmuste summa, korrutis, nende omadused, graafiline esitus. Sündmused jagunevad: 1. Juhuslik 2. Usaldusväärne 3. Võimatu Usaldusväärne on sündmus, mis teatud tingimustes (hommikule järgneb öö) tingimata aset leiab. Juhuslik sündmus on sündmus, mis võib juhtuda või mitte (eksami sooritamine). Võimatu sündmus on sündmus, mis etteantud tingimustel ei toimu (rohelise pliiatsi väljavõtmine karbist, kus on ainult punased). Lase zq on funktsiooni /(r) ainsuspunkt, t.s. f(z) kuid on selles punktis analüütiline (eelkõige ei pruugi see olla määratletud). Kui on selline torgatud naabruskond punkti zq (st hulk O z - zq f(z) on siis aialiline zo helistas isoleeritud ainsuse punkt funktsioonid f(z). See määratlus jääb samaks juhul zn = oo, kui jood on punkti lähedusest läbistatud zq = oo mõista komplekti z> I -
ringi väliskülg, mille keskpunkt on alguspunktis. Teisisõnu, eriline punkt zq on isoleeritud, kui selle punkti läheduses on ist muid ainsuse punkte peale zq. Alljärgnevas käsitleme ainult unikaalse iseloomuga ainsuse punkte (funktsioon f(z) eeldatakse, et see on üheselt mõistetav). Olenevalt funktsiooni käitumisest f(z) juures z -> zq Ainsuse punkte on kolme tüüpi. Eraldatud ainsuse punkt zq funktsioonid f(z) kutsus: 1) eemaldatav ainsuse punkt, kui on piiratud piir 2) poolus, kui on piir 3) sisuliselt eriline punkt, Kui f(z) ei oma lõplikku ega lõpmatut piiri at z-> zq. Näide 26.1. Näitame, et kõik kolm ainsuse punkti tüüpi on realiseeritud. Mõelgem f(z)= Punkt zq = 0 on isoleeritud selle funktsiooni eriline punkt. Valemi (22.12) abil saame laienduse millest järeldub, et eksisteerib lim fi(z)= 1. Seega zq = 0 on on funktsiooni eemaldatav ainsuse punkt fi(z). Funktsioon f'j(z) =---on punktis poolus zo= 1, sest 2
r"X Vaatleme nüüd funktsiooni )з(z)= e 1 ^ r ja näita seda zo = O on selle funktsiooni sisuliselt ainsuspunkt. Kui pingutada z nulli piki reaaltelge funktsiooni /z vasak ja parem piir (z) erinev: lim Koos 1 / 1
=
0, lim s 1 /* = os. See tähendab, x->0-0 x->0+O Mida f:i(z) ei ole lõplikku ega lõpmatut piiri 2 juures ->
Oh, see on. zq = O on selle funktsiooni sisuliselt ainsuse punkt. (Pange tähele, et nagu asi kipub z - iy nullini piki kujuteldavat teljefunktsiooni pole üldse piiranguid.) Muidugi on ka isoleerimata ainsuse punkte. Näiteks. funktsioonil on punktides poolused z n = -, P= ±1, ±2,... Seega Zq = 0 on selle funktsiooni isoleerimata ainsuse punkt: selle punkti mis tahes (ükskõik kui väikeses) läheduses on ka teisi ainsuse punkte g lk.
Lase zo- funktsiooni lõplik isoleeritud ainsuse punkt f(z). Siis f(z) on 0 Zo punkti mõnes torgatud piirkonnas sarnane zo seda naabrust võib pidada rõngaks siseraadiusega r = 0. Teoreemi 25.1 järgi võib vaadeldavas naabruses funktsioon f(z) saab laiendada Laurent'i seeriaks (25.2). Näitame, et funktsiooni käitumine punktis 2 -> zq (st ainsuse punkti tüüp zo) oleneb laienduse põhiosa tüübist (25.2); See asjaolu selgitab mõiste "põhiosa" päritolu. Teoreem 2G.2. Funktsiooni f(z) isoleeritud ainsuse punkt zo on eemaldatav siis ja ainult siis, kui Lorapovi laiendusel selle punkti punkteeritud ümbruses on oid need. koosneb ainult õigest osast, ja kõik põhiosa koefitsiendid on võrdsed kuuliga. Tõestus. 1. Lase zo- eemaldatav ainsuse punkt. Tõestame, et funktsiooni Laurent'i laiendus f(z) on kujul (26.1). Alates eripunktist zo eemaldatav, siis on olemas piiratud limiit f(z) = A. Seega f(z) on piiratud punkti 0 z - zq punkteeritud naabruskonnaga zo, need. )(z) kõigile z sellest lähedusest. Võtame ükskõik millise R. U р /?| ja kasutage Laurent'i seeria koefitsientide jaoks valemeid (25.3): Laienduse põhiosa koefitsientide jaoks n =- 1,-2,... Selliste väärtuste jaoks P meil on p~ lk-e 0 kl R-> 0. Alates väärtusest R saab valida suvaliselt väikese, siis härra ~" võib olla nii väike kui soovitakse. Kuna |s t,| ^ Mr~p ja c„ ei sõltu p-st, siis c„ = 0 at Ja= - 1, -2,..., mida oli vaja tõestada. 2. Oletame nüüd, et Laurent'i laiendil on vorm (26.1). Seeria (26.1) on astmerida ja. seetõttu koondub see mitte ainult torkepiirkonnas, vaid ka kogu läheduses z-zq sealhulgas punkt zo; selle summa S(z) on analüütiline juures z ja S(z) = )(z) 0 z juures - zo R. Seetõttu on olemas piiratud limiit )(z)= Pt 5(g) = 5(th) – Seega ainsuse punkt zq Z->Zo Z-*Zo eemaldatav. Teoreem on tõestatud. Kommenteeri. Teoreemi tõestusest järeldub, et eemaldatava ainsuse punkti punkteeritud ümbruses 0 z - zo on funktsioon f(z) langeb kokku funktsiooniga 5(r), mis on analüütiline kogu naabruskonnas z - zo. Seega, kui seame /(th) = S(zq), siis funktsiooni väärtusi muutmata f(z) torgatud naabruskonna mis tahes punktides muudame selle funktsiooni Go-s analüütiliseks, st. "Eemaldame" funktsiooni. See selgitab mõistet "eemaldatav funktsioon". On loomulik, et selliseid punkte peetakse funktsiooni korrapärasteks, mitte ainsusteks f(z).
Mõelge näiteks funktsioonile Näites 26.1 näidati, et Pm Nr) = 1. st. ainsuse punkt zq = 0 eemaldatav. Seadistades /i(0) = 1, kõrvaldame seeläbi singulaarsuse ja saame funktsiooni, mis on punktis analüütiline zq = 0 (ja kogu C-tasandil). Iseloomustame nüüd pooluseid Laurent'i laienduste järgi. Teoreem 26.3. Funktsiooni f(z) isoleeritud ainsuse punkt Zo on poolus siis ja ainult siis, kui Laurent'i laienduse põhiosal keskpunktiga Zq on ainult piiratud arv erinevaid nullkoefitsiendist n-ga: Tõestus. 1. Lase zq - poolus, st. lim/( z) = oo. Tõestame, et funktsiooni Laurent'i laiendus f(z) on kujul (2G.2). Kuna lim f(z)= oo. siis on punkti torgatud naabruskond ki zq. kus f(z) on analüütiline ja sellel puuduvad nullid. Siis funktsioon g(z) = 1 /f(z) on ka selles torgatud piirkonnas analüütiline ja lim g(z)= 0. Seetõttu Zo on eemaldatav *-? *0 funktsiooni ainsuse punkt g(z). Defineerime g(z) punktis zo, pannes g(zo)=
0. Siis g(z) muutub analüütiliseks kogu (mitte läbistatud) punkti naabruses z 0, ja z 0 on selle isoleeritud null. Tähistame tähisega N selle nulli kordsus (järk). Nagu näidati §23, punkti naabruses zq funktsioon g(z) saab esitada kujul (vt (23.2)) ja (z$) f 0 ja y>(z) on punkti mõnes naabruses analüütiline zo- Sest ip(z) pidev mingis punktis zo Ja g>(zo) Ф 0" siis ip(z) ei oma selle punkti mõnes naabruses nulle. Seetõttu funktsioon 1 /-p(z) on ka selles naabruskonnas analüütiline ja seetõttu laieneb see Taylori seerias: Sulgude avamisel ja koefitsientide tähistuste muutmisel kirjutame vormi viimase laienduse kus c_jv = 1>o f 0. Seega sisaldab funktsiooni /(r) Laurent'i laienduse põhiosa ainult lõplikku arvu termineid; oleme jõudnud soovitud võrdsuseni (26,2). 2. Laske sisse torgatud punktide ümbrus th funktsiooni )(z) on esindatud Laurent'i laiendiga (26.2) (täpsemat vormi vt (26.3)), mille põhiosa sisaldab vaid lõplikku arvu termineid ja Koos- d" f 0. Seda on vaja tõestada Zq - funktsioonipoolus f(z). Võrdsuse (26,3) korrutamine (G - G o) iV , saame funktsiooni Jada punktis (26.4) on astmerida, mis koondub analüütiliseks funktsiooniks mitte ainult läbitorkavas punktis, vaid ka kogu punkti naabruses Zq. Seetõttu funktsioon h(z) muutub selles naabruskonnas analüütiliseks, kui me seda täpsemalt defineerime laskmise teel h(zo)= s_dg f 0. Siis Seega on punkt th poolus ja teoreem 26.3 on tõestatud. Nullfunktsiooni kordsus (järk). g(z)= 1//(g) kutsutakse poolusjärjestus funktsioon /(r). Kui N- th pooluse järjekord, siis g(z)= (g - Zo) N ip(z), ja mine) F 0 ja nagu on näidatud teoreemi 26.3 tõestuse esimeses osas, on funktsiooni /(r) laiendus kujul (26.3), kus c_/v f 0. Ja vastupidi, kui /(r) laiendatakse seeriasse (26.3) ja e-i F 0 siis t.s. N- funktsiooni /(r) pooluse järjekord. Seega funktsiooni zq poolusjärk/(G) võrdne Laurent'i laienduse põhiosa kõrgeima nullist erineva koefitsiendi arvuga punkti zq torgatud ümbruses(st võrdne selle arvuga N, mida s_dg f 0 ja Sp= 0 at P > N). Tõestame järgmist väidet, mis on rakenduste jaoks mugav. Järeldus 26.4. Punkt zq on väljamõeldise N järku poolus/(G) siis ja ainult siis/(G) kujul esindatav kus h(z) on punkti läheduses olev analüütiline funktsioon th ja h(zo) f 0. Tõestus. Funktsioon cp(z) = l/h(z) on punkti h mõnes naabruses analüütiline. Järeldus 26.4 on samaväärne järgmisega: Sellepärast zq -
nullkordsus N funktsioonid g(z). ja seetõttu ka paljususe poolus N funktsioonid /(2). II Näide 26.5. Leia funktsiooni isoleeritud ainsuse punktid Lahendus: punktid, kus (z 2
+ 1 )(z+ Z) 2 = 0. Kui z 2
L- 1 = 0, siis 2 = ±g Kui (z 4- 3) 2 = 0, siis z= -3. Seetõttu on funktsioonil kolm ainsuse punkti z= g, 22 = -g, Z3
=
- 3. Kaaluge z: G - esimese järgu pulk (kasutasime järeldust 26.4). Sarnaselt saab tõestada, et 22 = -i ka esimest järku post. 2z jaoks on meil: Jätkame sisuliselt ainsuse punktide käsitlemisega. Teoreem 26.6. Funktsiooni f(z) isoleeritud ainsuse punkt zq on sisuliselt ainsus siis ja ainult siis, kui Laurent'i laienduse põhiosal keskpunktiga zq on lõpmata palju erinevaid. null, koefitsiendid alates p. Tõestus. Lause 26.6 tuleneb otseselt teoreemidest 26.2 ja 26.3. Tõepoolest, kui punkt zq on olemuselt eriline, siis ei saa Laurenti laienduse põhiosa puududa ega sisaldada lõplikku arvu termineid (muidu punkt Zq on kas eemaldatav või poolus). Seetõttu peab põhiosas olevate terminite arv olema lõpmatu. Ja vastupidi, kui põhiosa sisaldab lõpmatult palju termineid, siis Zq ei saa olla ei eemaldatav punkt ega poolus. Sellest järeldub, et see punkt on sisuliselt eriline. Definitsiooni järgi iseloomustab sisuliselt ainsuse punkti see, et funktsioonil /(2) ei ole lõplikku ega lõpmatut piiri z ->zq. Täielikuma ettekujutuse sellest, kui ebaregulaarne on funktsiooni käitumine sisuliselt ainsuse punkti läheduses, annab järgmine teoreem. Teoreem 26.7 (Sokhotski teoreem). Kui zq on inimeste jaoks oluline, siis funktsiooni punkt f(z), siis mis tahes kompleksarvu jaoks L, sealhulgas A = oh, on punktide jada z n nii, et z n -> zo ja lim f(zn) = A. p->os Tõestus. Vaatleme esmalt juhtumit A = oo. Teoreemi 2G.2 tõestuse esimeses osas tegime kindlaks, et kui f(z) on piiratud punkti r mingis punkteeritud naabruses, siis kõik koefitsiendid c", n = - 1,- 2,... põhiosast on võrdsed nulliga (ja seetõttu on singulaarsus in go eemaldatav). Kuna tingimuse järgi on th oluline ainsuse punkt, siis punkti th mis tahes punkteeritud ümbruses on funktsioon f(r) piiramata. Võtame mõne tugeva naabruskonna 0 Z, nii et f(zi) > 1 (kui |/(r)| z - zo I/2 on punkt z-2
, milles |/(yy)| > 2 jne: torgatud naabruses O 71.
On ilmne, et r„ -e go ja lim /(r“) = oo. Seega juhul A = oo, teoreem 26.7 tõestatud. Las see nüüd A f oo. Oletame esmalt, et seal on torgatud naabruskond 0 = -yy----
on selles torgatud piirkonnas analüütiline ja sellest tulenevalt /(G) - A Järelikult on go funktsiooni Φ(r) isoleeritud ainsuse punkt. Me näitame teile. et r on Φ(r) sisuliselt ainsuse punkt. See ei pruugi tõsi olla. Siis on piir lim Ф(r), lõplik või lõpmatu. Mõneks ajaks /(r) = A + , siis on ka Hsh /(r), mis on tingimusega vastuolus F(g) ~ :-*z 0 Ma näen teoreemi. Seega on r0 funktsiooni Φ(r) sisuliselt ainsuse punkt. Eespool tõestatu kohaselt on punktide jada r n selline, et r n th ja lim Ф(r n) = oo. Siit Oleme tõestanud nõutavat väidet eeldusel, et /(r) F A mõnes punktsiooniga naabruses punkti mine- Oletame nüüd, et see on vale, st. punkti th suvaliselt väikeses torgatud naabruses on selline punkt G", et /(r") = L. Siis mis tahes jaoks P punkteeritud piirkonnas 0 f(z u) = А. Seega on soovitud väide tõene P-juu kõigil juhtudel ja teoreem 26.7 on tõestatud. Vastavalt teoreemile 26.7 (Sokhotsky) omandab funktsioon /(r) sisuliselt ainsuse punkti mis tahes (meelevaldselt väikeses) torgatud piirkonnas väärtused, mis on meelevaldselt lähedased mis tahes arvule laiendatud komplekstasandist C. Eraldatud ainsuse punktide uurimiseks on sageli kasulikud põhiliste elementaarfunktsioonide juba tuntud Taylori laiendused. Näide 2G.8. Määrake funktsiooni ainsuse punkti tüüp zq = 0 Lahendatud ja e. Laiendame lugeja ja nimetaja Taylori seeriaks g astmetes. Asendame punktis (22.11) 3 z r asemel ja lahutada 1, saame Kasutades (22.12) saame nimetaja laienduse: Nende laienduste seeriad koonduvad kogu komplekstasandil €. Meil on ja /2(2) on punkti naabruses anariidid zo = 0 (ja isegi kogu tasapinnas) ja /2 (20) F 0 siis h(z) on ka analüütiline mõnes punkti gF 0 naabruses. Järeldus 26.4 kohaselt on punkt Zo = 0 on järjekorra poolus N = 4. II Näide 26.9. Funktsiooni ainsuse punktide leidmine f(z)= sin j - ja määrake nende tüüp. R e in e i e Funktsioonil on üks lõplik ainsuse punkt zq = 1. Teistes punktides C-st funktsioon w =--- analüütiline; siit ka funktsioon sin w saab olema analüütiline. Asendades - r asemel siinuse (22.12) laienduseks saame Oleme saanud funktsiooni sin laienduse Laurent'i jadaks punkti 2o = 1 punkteeritud ümbruses. Kuna saadud laiendus sisaldab lõpmatult palju negatiivsete võimsustega (r - 1) liikmeid, siis zq = 1 on sisuliselt ainsuse punkt (sel juhul koosneb Laurent'i laiend ainult põhiosast ja tavaline osa puudub). Pange tähele, et singulaarsuse olemust oli sel juhul võimalik kindlaks teha otse definitsioonist, ilma seeria laiendamist kasutamata. Tõepoolest, seal on jadad (r",) ja (2"), mis koonduvad zo= 1 ja selline f(z"n)= 1, /(2") = 0 (näidake sellised jadad ise). f(z) ei ole piirangut z -> 1 ja seega punkt zq - 1 on sisuliselt eriline. Tutvustame funktsiooni Laurent'i laienduse mõistet punkti läheduses Zq = 00 ja kaaluge siinkohal seost laienemise ja singulaarsuse olemuse vahel. Pange tähele, et isoleeritud ainsuse punkti ja selle tüübi (eemaldatav, poolus või sisuliselt ainsus) määratlused kanduvad üle juhtumile zq = oc ilma muudatusteta. Kuid teoreemid 26.2. Laurenti laienduste olemusega seotud 26.3 ja 26.6 tuleb muuta. Asi on selles, et liikmed cn(z- 2o) lk. P= -1,-2,..., põhiosa, mis määrab funktsiooni "ebakorrapärasuse" lõpp-punkti lähedal Zq, kuna 2 kipub olema oo, käituvad nad "õigesti" (kalduvad 0-le). Vastupidi, õige osa liikmed koos P= 1,2,... kipub oo; need määravad tunnuse olemuse Zq = oo. Seetõttu moodustavad suurema osa oo ümbruse laienemisest positiivsete jõududega terminid P, ja õige – negatiivsetega. Tutvustame uut muutujat w = 12. Funktsioon tv = 1/2, laiendatud nii, et u(oo) = 0, üks-ühele ja kaardistab naabruskonna konformselt z > R punktid zq = 00 |w| läheduses wq = 0. Kui funktsioon f(z) analüütika torgatud naabruskonnas R z Zq = oc, siis funktsioon G(w) = f(l/w) on suures naabruses analüütiline 0 wo = 0. Kuna kell 2 -> oo on w-> 0 siis Sellepärast G(w) on punktis wq = 0 on sama tüüpi tunnus kui f(z) punktis Zq = 00. Laiendame funktsiooni G(w) Laurent'i seeriaks punkti wo = 0 punkteeritud ümbruses: (26.5) paremal küljel olevad summad tähistavad vastavalt laienduse tava- ja põhiosa. Liigume edasi muutuja juurde z, asendamine w = 1/z: Määramine P= -A*, 6* = 6_„ = s p ja seda märgates G(l/z) = f(z), saame Lagunemist (2G.G) nimetatakse Funktsiooni f(z) Laurent'i laiendus punkti zq punkteeritud ümbruses= oo. Esimest summat (2G.6) nimetatakse õige osa, ja teine summa on põhiosa sellest lagunemisest. Kuna need summad vastavad laienduse õigetele ja peamistele osadele (26.5), siis laienduseks (26.6) kehtivad teoreemide 26.2, 26.3 ja 26.6 analoogid. Seega on järgnev teoreem teoreemi 26.2 analoog. Teoreem 26.10. Eraldatud ainsuse punktZq -
OS (funktsioonid/(G) on eemaldatav siis ja ainult siis, kui Laurent'i laiendusel selle punkti torgatud naabruses on vorm
t.s. koosneb ainult õigest osast. Paneme /(oo) = co. Funktsioon, mis on määratletud naabruses koonduva seeriaga (26.7). z > R punkt 2o = oc, nn analüütiline punktis z o = oo. (Pange tähele, et see määratlus on samaväärne funktsiooni analüütilisusega G(w) punktis vau = 0.) Näide 26.11. Uurige funktsiooni ainsuse punkti zq = oo Kuna piir on piiratud, siis zo = oo on funktsiooni /(r) eemaldatav ainsuse punkt. Kui paneme /(oo) = lim J(z)= 0, siis f(z) muutub analüütiliseks tic punktis Zo= os. Näitame, kuidas leida vastav laiend (26.7). Liigume edasi muutuja juurde w = 1 fz. Asendamine z= 1 /?е, saame (viimane võrdus kehtib punkti wо = 0 punkteeritud ümbruses, kuid me defineerime edasi (7(0) = 0). Saadud funktsioonil on ainsuse punktid w =± mina, w =-1/3 ja punktis Wq = 0 on analüütiline. Avamisfunktsioon G(w) kraadide kaupa w(nagu tehti näites 25.7) ja asendades saadud astmerida w = 1/z, saame funktsiooni laienduse (26.7). f(z).
Teoreem 26.3 juhtumi jaoks zo= oo kirjutatakse ümber järgmisel kujul. Teoreem 26.12. Eraldatud ainsuse punkt th = os funktsioon f(z) on poolus siis ja ainult siis, kui Laurent'i laienduse põhiosa (26.6) sellel on ainult piiratud arv nullist erinevaid koefitsiente Koos": Siin on seeria tavaline osa ja sulgudes olev polünoom on laienduse põhiosa. Pooluste kordsus oc-s on defineeritud pooluste kordsusena wq = 0 funktsiooni G(z). On lihtne näha, et pooluse kordsus langeb kokku arvuga N aastal (26.8). Q p | (i 2 + 1) (z+3) 2 Ülesanne. Näidake, et funktsioon f(z) =--
-- on sees punkt zo = oo järjestuspoolus 3. Teoreem 26.6 sisuliselt ainsuse punkti kohta saab juhtumi jaoks ümber kirjutada zo= os peaaegu sõna-sõnalt ja me ei peatu sellel üksikasjalikult.
, võetud positiivses suunas mööda ringjoont L, mille keskpunkt on punktis z 0, mis asub funktsiooni f(z) analüütilisuse piirkonnas (st ringis 0<|z-z0| . (22.15.1)
ja määrake nende tüüp.
Laadimine...
